第五章 《平行四边形》复习与巩固学案
文档属性
| 名称 | 第五章 《平行四边形》复习与巩固学案 |

|
|
| 格式 | docx | ||
| 文件大小 | 329.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-28 15:26:29 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
《平行四边形》复习与巩固
【学习目标】
1.能够熟练掌握平行四边形的判定和性质定理,并能够应用数学符号语言表述证明过程.
2.掌握三角形中位线的定义和性质,明确三角形中位线与中线的不同并能运用它进行有关的论证和计算.
3.掌握多边形内角和、外角和定理,进一步了解转化的数学思想.
【课前梳理】
1.定义:________________________________________的四边形是平行四边形.
2.平行四边形的性质(边,角,对角线,对称性)
(1)边的性质:平行四边形的对边_________;平行四边形的对边__________;
(2)角的性质:平行四边形的对角________ ;
(3)对角线的性质:平行四边形的对角线__________________;
(4)平行四边形是__________对称图形 .
3.平行四边形的判定.
(1)两组对边__________________________的四边形是平行四边形(定义);
(2)两组对边__________________________的四边形是平行四边形 ;
(3) 对角线___________________________的四边形是平行四边形 ;
(4)一组对边__________________________的四边形是平行四边形;
(5)两组对角__________________________的四边形是平行四边形 .
4.两条平行线间的距离的定义.
若两条直线互相平行,则其中一条直线上任意_______到另一条直线的________相等,这个________称为平行线之间的距离,实际上________________________处处相等.
5.三角形的中位线 .
(1)三角形中位线的定义:连接________________________的线段叫做三角形的中位线 ;
(2)三角形中位线定理:三角形的中位线____________第三边,且等于______________.
6.多边形的内角与外角和 .
(1)多边形:在平面内,由______________________________________________组成的封闭图形叫做多边形 ;
(2)n边形的内角和是________________________;
(3)多边形的外角和等于_____________________.
【课堂练习】
典型例题1
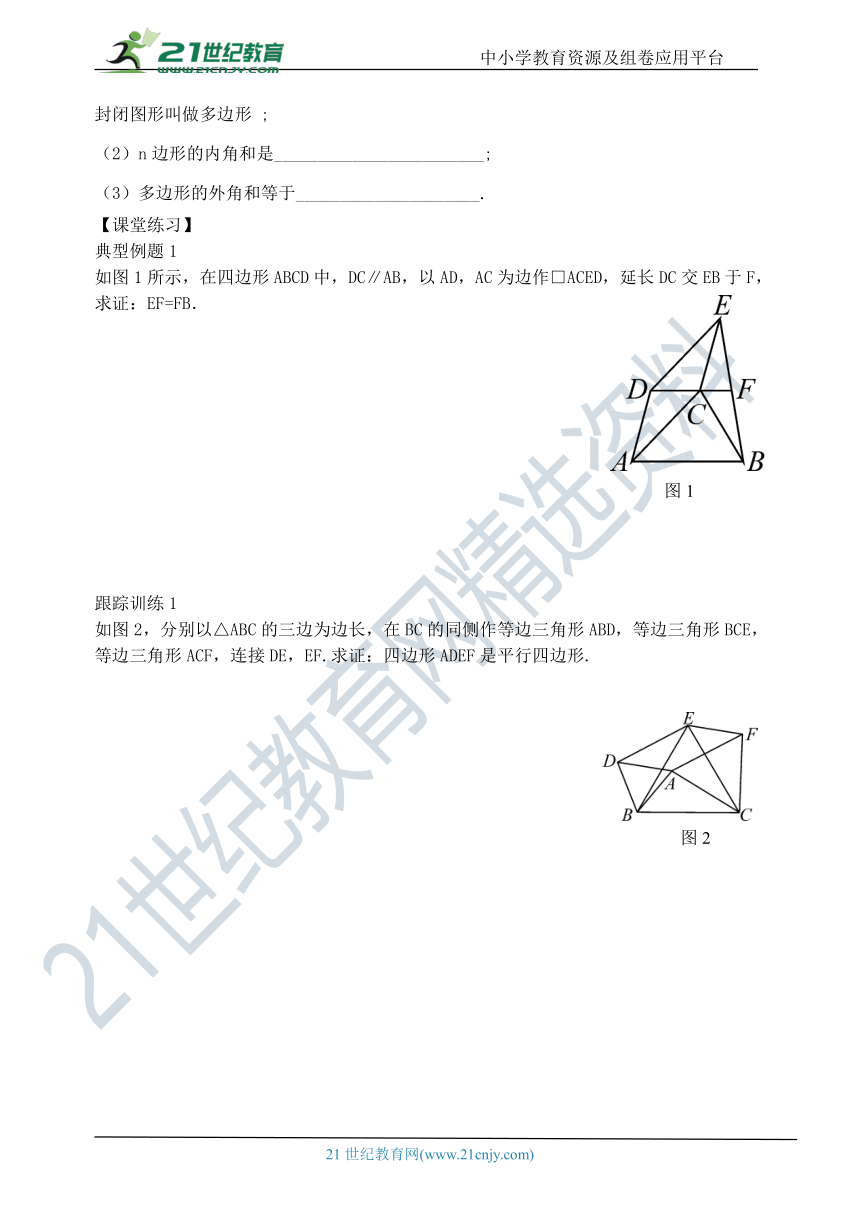
如图1所示,在四边形ABCD中,DC∥AB,以AD,AC为边作□ACED,延长DC交EB于F,求证:EF=FB.
跟踪训练1
如图2,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF.求证:四边形ADEF是平行四边形.
典型例题2
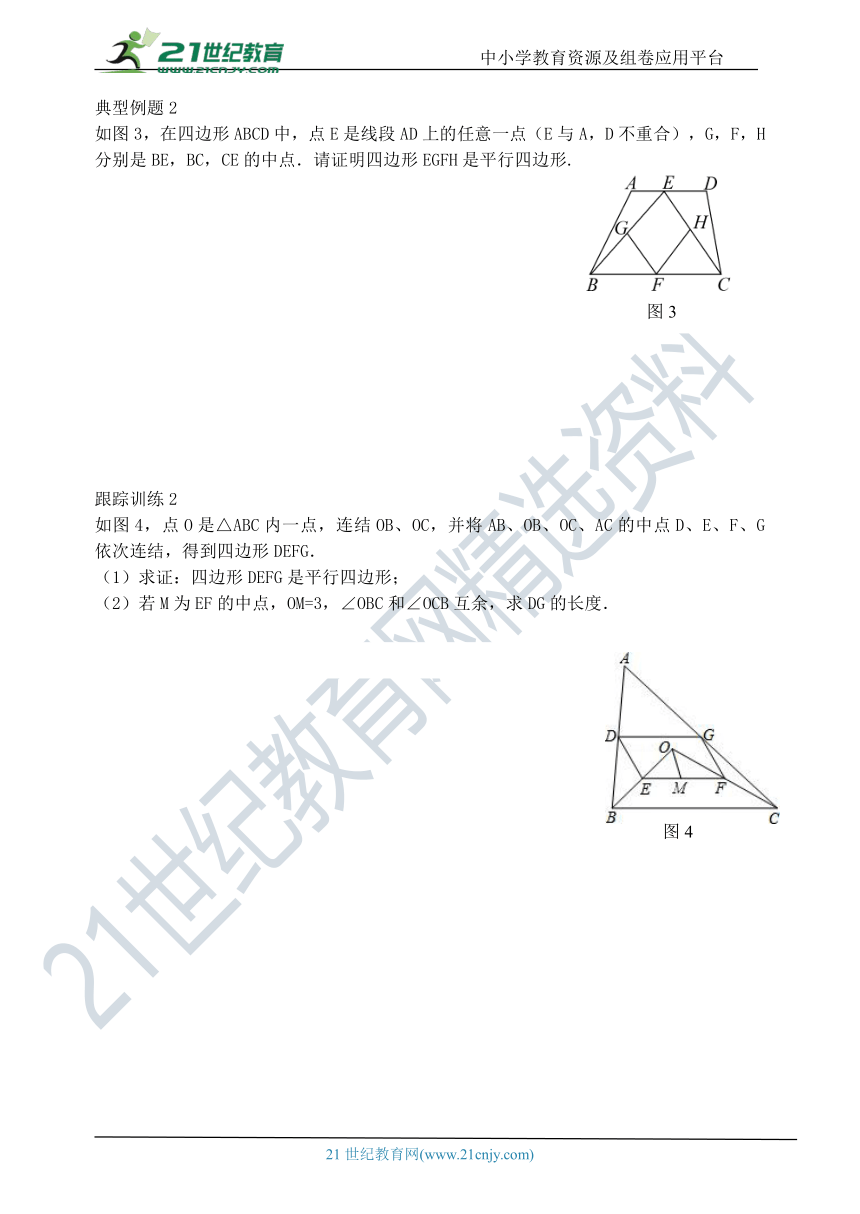
如图3,在四边形ABCD中,点E是线段AD上的任意一点(E与A,D不重合),G,F,H分别是BE,BC,CE的中点.请证明四边形EGFH是平行四边形.
跟踪训练2
如图4,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
【巩固训练】
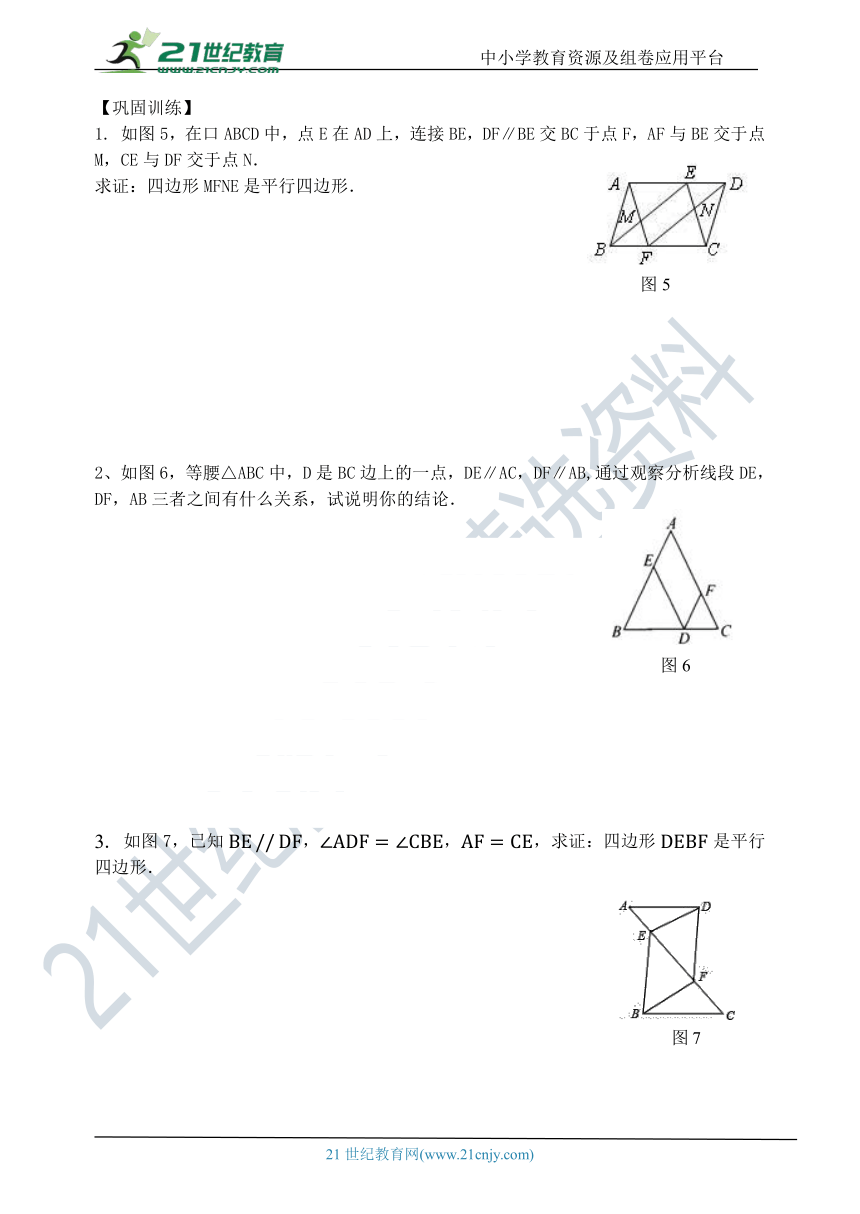
如图5,在口ABCD中,点E在AD上,连接BE,DF∥BE交BC于点F,AF与BE交于点M,CE与DF交于点N.
求证:四边形MFNE是平行四边形.
2、如图6,等腰△ABC中,D是BC边上的一点,DE∥AC,DF∥AB,通过观察分析线段DE,DF,AB三者之间有什么关系,试说明你的结论.
3. 如图7,已知,,,求证:四边形是平行四边形.
4. 如图8,在中,,,是的平分线,.
求的度数;
(2)求的长.
5. 公园有一片绿地,它的形状是平行四边形,绿地上要修几条笔直的小路,如图9,,,,求:
(1)小路,,的长;
(2)计算出绿地的面积;
(3)、之间的距离.
6. 已知:如图10,平行四边形中,、、、分别平分、、、,、的延长线分别交、于点、,连接,若,,求的长.
第五章复习答案
典型例题1
如图1所示,在四边形ABCD中,DC∥AB,以AD,AC为边作□ACED,延长DC交EB于F,求证:EF=FB.
证明:过点B作BG∥AD,交DC的延长线于G,连接EG.
∵DC∥AB,∴ABGD是平行四边形,
∴BGAD.
在□ACED中,ADCE,∴CEBG.
∴四边形BCEG为平行四边形,∴EF=FB.
跟踪训练1
如图2,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF.求证:四边形ADEF是平行四边形.
解析:先证△EDB≌△CFE,
可得BD=EF,ED=CF.
∵BD=DA,CF=AF,
∴ED=AF,EF=DA,
∴四边形ADEF是平行四边形.
典型例题2
如图3,在四边形ABCD中,点E是线段AD上的任意一点(E与A,D不重合),G,F,H分别是BE,BC,CE的中点.请证明四边形EGFH是平行四边形.
证明:在△BEC中,∵G,F分别是BE,BC的中点,
∴GF∥EC且GF=EC .
又∵H是EC的中点,EH=EC,
∴GF∥EH且GF=EH .
∴四边形EGFH是平行四边形.
跟踪训练2
如图4,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
1)在 ABCD中,AD∥BC,
∵DF∥BE,
∴四边形BFDE是平行四边形,
∴DE=BF;
(2)在 ABCD中,AD∥BC且AD=BC,
∵DE=BF,
∴AD DE=BC BF,
即AE=CF,
∴四边形AFCE是平行四边形,
∴AF∥CE,
∵四边形BFDE是平行四边形,
∴DF∥BE,
∴四边形MFNE是平行四边形。
【巩固训练】
1.证明:在 ABCD中,AD∥BC且AD=BC,
∵DE=BF,
∴AD DE=BC BF,
即AE=CF,
∴四边形AFCE是平行四边形,
∴AF∥CE,
∵四边形BFDE是平行四边形,
∴DF∥BE,
∴四边形MFNE是平行四边形。
2.解答:
AB=DE+DF.
理由:∵DE∥AC,DF∥AB
∴四边形AEDF是平行四边形,∠C=∠EDB
∴DF=AE
∵等腰△ABC
∴∠B=∠C
∴∠B=∠EDB
∴DE=BE
∴AB=AE+BE=DF+DE.
3.证明:∵ ,
∴ ,
在和中,
∴ ,
∴ ,
又∵ ,
∴ 四边形是平行四边形.
4.解:(1)∵ 是的平分线,
∴ ,
∵ ,
∴ .
(2)∵ ,是的平分线,
∴ 为的中点,
∵ ,
∴ 为的中点,
∴ .
5.
解:(1)∵ 四边形是平行四边形,
∴ ,,,
∴ ,,
∵ ,
∴ ,
∴ ;
(2)绿地的面积为:;
(3)设、之间的距离为,
∵ 绿地的面积为:,
∴ ,
解得:.
6.
解:∵ 四边形是平行四边形,
∴ ,,.
∴ .
∵ 平分,
∴ .
∴ .
∴ .
∵ 平分,
∴ ,
.同理,,,
∴ .
∴ ,即 .
∴ 四边形是平行四边形,
∴ ,.
∴ ,.
∴ 四边形是平行四边形.
∴ .
∵ ,
∴ .
21世纪教育网(www.21cnjy.com)
《平行四边形》复习与巩固
【学习目标】
1.能够熟练掌握平行四边形的判定和性质定理,并能够应用数学符号语言表述证明过程.
2.掌握三角形中位线的定义和性质,明确三角形中位线与中线的不同并能运用它进行有关的论证和计算.
3.掌握多边形内角和、外角和定理,进一步了解转化的数学思想.
【课前梳理】
1.定义:________________________________________的四边形是平行四边形.
2.平行四边形的性质(边,角,对角线,对称性)
(1)边的性质:平行四边形的对边_________;平行四边形的对边__________;
(2)角的性质:平行四边形的对角________ ;
(3)对角线的性质:平行四边形的对角线__________________;
(4)平行四边形是__________对称图形 .
3.平行四边形的判定.
(1)两组对边__________________________的四边形是平行四边形(定义);
(2)两组对边__________________________的四边形是平行四边形 ;
(3) 对角线___________________________的四边形是平行四边形 ;
(4)一组对边__________________________的四边形是平行四边形;
(5)两组对角__________________________的四边形是平行四边形 .
4.两条平行线间的距离的定义.
若两条直线互相平行,则其中一条直线上任意_______到另一条直线的________相等,这个________称为平行线之间的距离,实际上________________________处处相等.
5.三角形的中位线 .
(1)三角形中位线的定义:连接________________________的线段叫做三角形的中位线 ;
(2)三角形中位线定理:三角形的中位线____________第三边,且等于______________.
6.多边形的内角与外角和 .
(1)多边形:在平面内,由______________________________________________组成的封闭图形叫做多边形 ;
(2)n边形的内角和是________________________;
(3)多边形的外角和等于_____________________.
【课堂练习】
典型例题1
如图1所示,在四边形ABCD中,DC∥AB,以AD,AC为边作□ACED,延长DC交EB于F,求证:EF=FB.
跟踪训练1
如图2,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF.求证:四边形ADEF是平行四边形.
典型例题2
如图3,在四边形ABCD中,点E是线段AD上的任意一点(E与A,D不重合),G,F,H分别是BE,BC,CE的中点.请证明四边形EGFH是平行四边形.
跟踪训练2
如图4,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
【巩固训练】
如图5,在口ABCD中,点E在AD上,连接BE,DF∥BE交BC于点F,AF与BE交于点M,CE与DF交于点N.
求证:四边形MFNE是平行四边形.
2、如图6,等腰△ABC中,D是BC边上的一点,DE∥AC,DF∥AB,通过观察分析线段DE,DF,AB三者之间有什么关系,试说明你的结论.
3. 如图7,已知,,,求证:四边形是平行四边形.
4. 如图8,在中,,,是的平分线,.
求的度数;
(2)求的长.
5. 公园有一片绿地,它的形状是平行四边形,绿地上要修几条笔直的小路,如图9,,,,求:
(1)小路,,的长;
(2)计算出绿地的面积;
(3)、之间的距离.
6. 已知:如图10,平行四边形中,、、、分别平分、、、,、的延长线分别交、于点、,连接,若,,求的长.
第五章复习答案
典型例题1
如图1所示,在四边形ABCD中,DC∥AB,以AD,AC为边作□ACED,延长DC交EB于F,求证:EF=FB.
证明:过点B作BG∥AD,交DC的延长线于G,连接EG.
∵DC∥AB,∴ABGD是平行四边形,
∴BGAD.
在□ACED中,ADCE,∴CEBG.
∴四边形BCEG为平行四边形,∴EF=FB.
跟踪训练1
如图2,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF.求证:四边形ADEF是平行四边形.
解析:先证△EDB≌△CFE,
可得BD=EF,ED=CF.
∵BD=DA,CF=AF,
∴ED=AF,EF=DA,
∴四边形ADEF是平行四边形.
典型例题2
如图3,在四边形ABCD中,点E是线段AD上的任意一点(E与A,D不重合),G,F,H分别是BE,BC,CE的中点.请证明四边形EGFH是平行四边形.
证明:在△BEC中,∵G,F分别是BE,BC的中点,
∴GF∥EC且GF=EC .
又∵H是EC的中点,EH=EC,
∴GF∥EH且GF=EH .
∴四边形EGFH是平行四边形.
跟踪训练2
如图4,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
1)在 ABCD中,AD∥BC,
∵DF∥BE,
∴四边形BFDE是平行四边形,
∴DE=BF;
(2)在 ABCD中,AD∥BC且AD=BC,
∵DE=BF,
∴AD DE=BC BF,
即AE=CF,
∴四边形AFCE是平行四边形,
∴AF∥CE,
∵四边形BFDE是平行四边形,
∴DF∥BE,
∴四边形MFNE是平行四边形。
【巩固训练】
1.证明:在 ABCD中,AD∥BC且AD=BC,
∵DE=BF,
∴AD DE=BC BF,
即AE=CF,
∴四边形AFCE是平行四边形,
∴AF∥CE,
∵四边形BFDE是平行四边形,
∴DF∥BE,
∴四边形MFNE是平行四边形。
2.解答:
AB=DE+DF.
理由:∵DE∥AC,DF∥AB
∴四边形AEDF是平行四边形,∠C=∠EDB
∴DF=AE
∵等腰△ABC
∴∠B=∠C
∴∠B=∠EDB
∴DE=BE
∴AB=AE+BE=DF+DE.
3.证明:∵ ,
∴ ,
在和中,
∴ ,
∴ ,
又∵ ,
∴ 四边形是平行四边形.
4.解:(1)∵ 是的平分线,
∴ ,
∵ ,
∴ .
(2)∵ ,是的平分线,
∴ 为的中点,
∵ ,
∴ 为的中点,
∴ .
5.
解:(1)∵ 四边形是平行四边形,
∴ ,,,
∴ ,,
∵ ,
∴ ,
∴ ;
(2)绿地的面积为:;
(3)设、之间的距离为,
∵ 绿地的面积为:,
∴ ,
解得:.
6.
解:∵ 四边形是平行四边形,
∴ ,,.
∴ .
∵ 平分,
∴ .
∴ .
∴ .
∵ 平分,
∴ ,
.同理,,,
∴ .
∴ ,即 .
∴ 四边形是平行四边形,
∴ ,.
∴ ,.
∴ 四边形是平行四边形.
∴ .
∵ ,
∴ .
21世纪教育网(www.21cnjy.com)
