4.1图形的平移(第4课时)课件(共15张PPT)
文档属性
| 名称 | 4.1图形的平移(第4课时)课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 608.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-01 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
4.1 图形的平移(4)
【学习目标】
在直角坐标系中,能写出一个已知顶点坐标的多边形沿坐标轴方向平移后图形.
1、直角坐标系中的点沿x轴方向平移a(a>0)个单位长度:
(x , y)
(x+a , y)
2、直角坐标系中的点沿y轴方向平移a(a>0)个单位长度:
向右平移a个单位
向左平移a个单位
(x-a , y)
(x , y)
(x , y+a)
向上平移a个单位
向下平移a个单位
(x , y-a)
回顾
1. (x,y) (x,y+4)
2. (x,y) (x,y-2)
4. (x,y) (3+x , y)
3. (x,y) (x-1, y)
口答练习:
在坐标系中,将坐标作如下变化时,图形将怎样变化?
思考:5. (x,y) (x-1 , y+4)
例1、
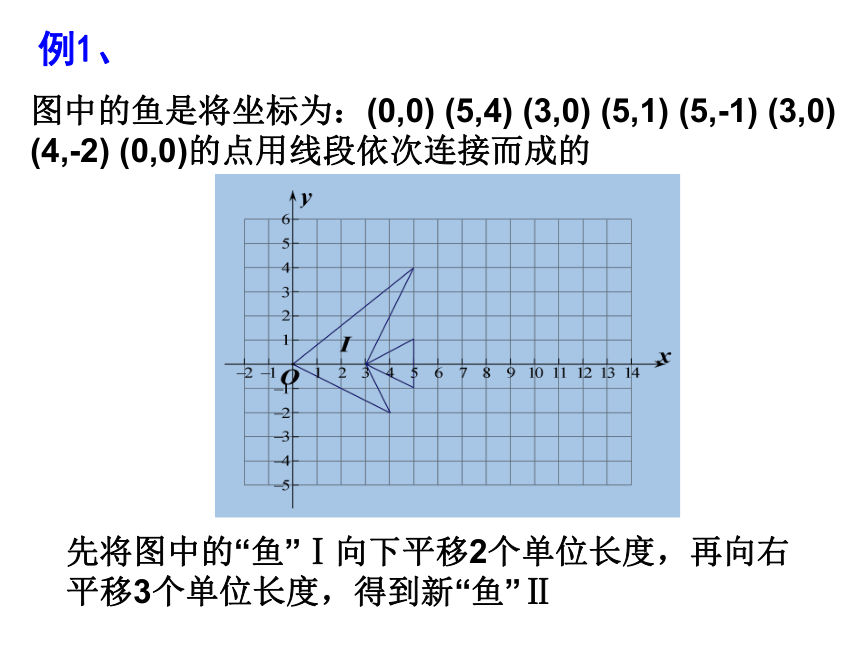
图中的鱼是将坐标为:(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)的点用线段依次连接而成的
先将图中的“鱼”Ⅰ向下平移2个单位长度,再向右平移3个单位长度,得到新“鱼”Ⅱ
(3)在“鱼”Ⅰ和“鱼”Ⅱ中,对应点的坐标之间有什么关系?
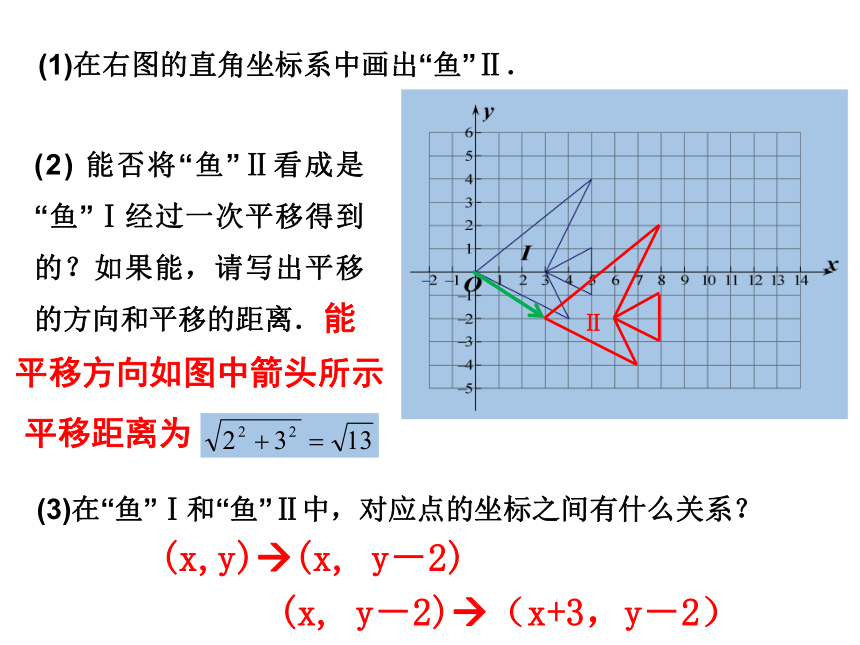
(1)在右图的直角坐标系中画出“鱼”Ⅱ.
(2) 能否将“鱼”Ⅱ看成是“鱼”Ⅰ经过一次平移得到的?如果能,请写出平移的方向和平移的距离.
能
平移方向如图中箭头所示
平移距离为
(x,y) (x, y-2)
(x, y-2) (x+3,y-2)
Ⅱ
做一做
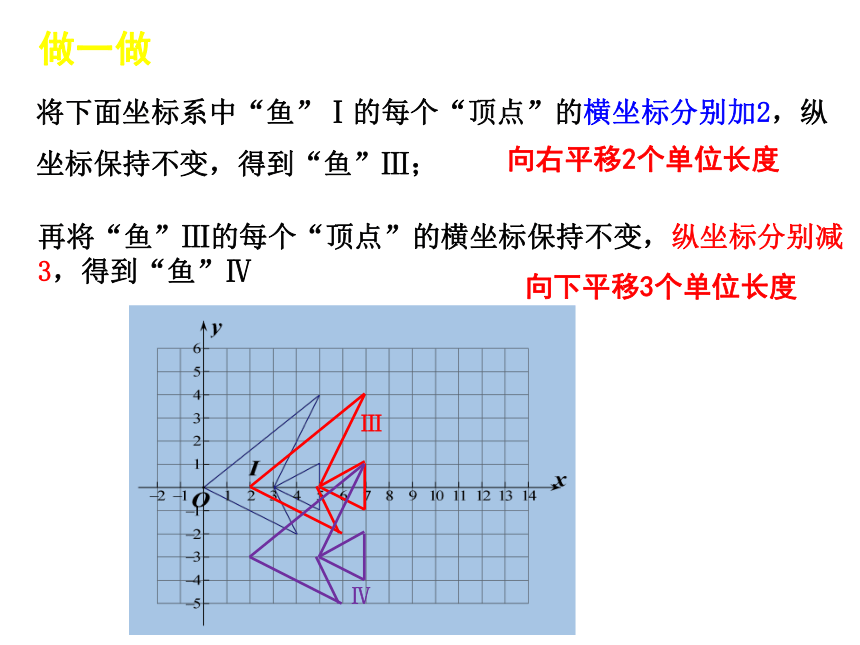
将下面坐标系中“鱼”Ⅰ的每个“顶点”的横坐标分别加2,纵坐标保持不变,得到“鱼”Ⅲ;
再将“鱼”Ⅲ的每个“顶点”的横坐标保持不变,纵坐标分别减3,得到“鱼”Ⅳ
向右平移2个单位长度
向下平移3个单位长度
Ⅲ
Ⅳ
(1)“鱼”Ⅳ与原来的“鱼”Ⅰ相比,有什么变化?
(2)能否将“鱼”Ⅳ看成是原来的“鱼”Ⅰ经过一次平移得到的?
(3)如果将 “鱼”Ⅰ的每个“顶点”的横坐标分别加2、纵坐标分别减3,得到的“鱼”与“鱼”Ⅳ相比,你有什么发现?
每个顶点的横坐标分别加2,纵坐标分别减3
Ⅲ
Ⅳ
能
得到的“鱼”与“鱼”Ⅳ是同一条“鱼”
议一议
一个图形依次沿x轴方向、y轴方向平移后所得图形与原来的图形相比,位置有什么变化?它们对应点的坐标之间有怎样的关系?
口答练习:
在坐标系中,将坐标作如下变化时,图形将怎样变化?
(x,y) (x-1 , y+4)
例题
如图,点A,B,C的坐标分别是A(1,-1)B(3,1)C(2,3),将△ABC平移后得到△AˊBˊ Cˊ,点A(1,-1)平移到Aˊ(-3,1)
(1)写出Bˊ、 Cˊ的坐标;
(2)画出△AˊBˊ Cˊ
分析:点A(1,-1)平移到Aˊ(-3,1)时,横坐标减小了4,纵坐标增加了2,所以Bˊ、 Cˊ两点的横坐标比B 、C两点的横坐标也应分别减小4,而纵坐标分别增加2.
Bˊ(3-4 ,1+2),即(-1,3)
Cˊ(2-4 ,3+2),
即(-2,5)
Bˊ
Cˊ
练一练
平移小结
1.纵坐标不变,横坐标分别增加(减少)a个单位时,图形 平移 a个 单位;
2.横坐标不变,纵坐标分别增加(减少) a个单位时,图形 平移a个单位;
向右(向左)
向上(向下)
3.横坐标分别增加(减少) a个单位、纵坐标分别增加(减少) b个单位时,图形是怎样平移的?请你与同学交流,并总结有哪几种平移方式。
作业布置
课本P89 习题4.4 知识技能
4.1 图形的平移(4)
【学习目标】
在直角坐标系中,能写出一个已知顶点坐标的多边形沿坐标轴方向平移后图形.
1、直角坐标系中的点沿x轴方向平移a(a>0)个单位长度:
(x , y)
(x+a , y)
2、直角坐标系中的点沿y轴方向平移a(a>0)个单位长度:
向右平移a个单位
向左平移a个单位
(x-a , y)
(x , y)
(x , y+a)
向上平移a个单位
向下平移a个单位
(x , y-a)
回顾
1. (x,y) (x,y+4)
2. (x,y) (x,y-2)
4. (x,y) (3+x , y)
3. (x,y) (x-1, y)
口答练习:
在坐标系中,将坐标作如下变化时,图形将怎样变化?
思考:5. (x,y) (x-1 , y+4)
例1、
图中的鱼是将坐标为:(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)的点用线段依次连接而成的
先将图中的“鱼”Ⅰ向下平移2个单位长度,再向右平移3个单位长度,得到新“鱼”Ⅱ
(3)在“鱼”Ⅰ和“鱼”Ⅱ中,对应点的坐标之间有什么关系?
(1)在右图的直角坐标系中画出“鱼”Ⅱ.
(2) 能否将“鱼”Ⅱ看成是“鱼”Ⅰ经过一次平移得到的?如果能,请写出平移的方向和平移的距离.
能
平移方向如图中箭头所示
平移距离为
(x,y) (x, y-2)
(x, y-2) (x+3,y-2)
Ⅱ
做一做
将下面坐标系中“鱼”Ⅰ的每个“顶点”的横坐标分别加2,纵坐标保持不变,得到“鱼”Ⅲ;
再将“鱼”Ⅲ的每个“顶点”的横坐标保持不变,纵坐标分别减3,得到“鱼”Ⅳ
向右平移2个单位长度
向下平移3个单位长度
Ⅲ
Ⅳ
(1)“鱼”Ⅳ与原来的“鱼”Ⅰ相比,有什么变化?
(2)能否将“鱼”Ⅳ看成是原来的“鱼”Ⅰ经过一次平移得到的?
(3)如果将 “鱼”Ⅰ的每个“顶点”的横坐标分别加2、纵坐标分别减3,得到的“鱼”与“鱼”Ⅳ相比,你有什么发现?
每个顶点的横坐标分别加2,纵坐标分别减3
Ⅲ
Ⅳ
能
得到的“鱼”与“鱼”Ⅳ是同一条“鱼”
议一议
一个图形依次沿x轴方向、y轴方向平移后所得图形与原来的图形相比,位置有什么变化?它们对应点的坐标之间有怎样的关系?
口答练习:
在坐标系中,将坐标作如下变化时,图形将怎样变化?
(x,y) (x-1 , y+4)
例题
如图,点A,B,C的坐标分别是A(1,-1)B(3,1)C(2,3),将△ABC平移后得到△AˊBˊ Cˊ,点A(1,-1)平移到Aˊ(-3,1)
(1)写出Bˊ、 Cˊ的坐标;
(2)画出△AˊBˊ Cˊ
分析:点A(1,-1)平移到Aˊ(-3,1)时,横坐标减小了4,纵坐标增加了2,所以Bˊ、 Cˊ两点的横坐标比B 、C两点的横坐标也应分别减小4,而纵坐标分别增加2.
Bˊ(3-4 ,1+2),即(-1,3)
Cˊ(2-4 ,3+2),
即(-2,5)
Bˊ
Cˊ
练一练
平移小结
1.纵坐标不变,横坐标分别增加(减少)a个单位时,图形 平移 a个 单位;
2.横坐标不变,纵坐标分别增加(减少) a个单位时,图形 平移a个单位;
向右(向左)
向上(向下)
3.横坐标分别增加(减少) a个单位、纵坐标分别增加(减少) b个单位时,图形是怎样平移的?请你与同学交流,并总结有哪几种平移方式。
作业布置
课本P89 习题4.4 知识技能
