4.2 图形的旋转(第1课时)课件(共12张PPT)
文档属性
| 名称 | 4.2 图形的旋转(第1课时)课件(共12张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 861.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-01 06:11:48 | ||
图片预览




文档简介
(共12张PPT)
第四章 图形的平移与旋转
【学习目标】
1.通过对生活中与旋转现象有关的图形进行观察、分析,以及动手操作、画图等过程,掌握有关的画图技能。
2.通过具体实例认识旋转,理解旋转前后两个图形对应点到旋转中心距离相等,对应点与旋转中心的连线所成的角彼此相等的性质,发展初步的审美能力。
观察思考
F
︵
A
B
C
D
E
O
︵
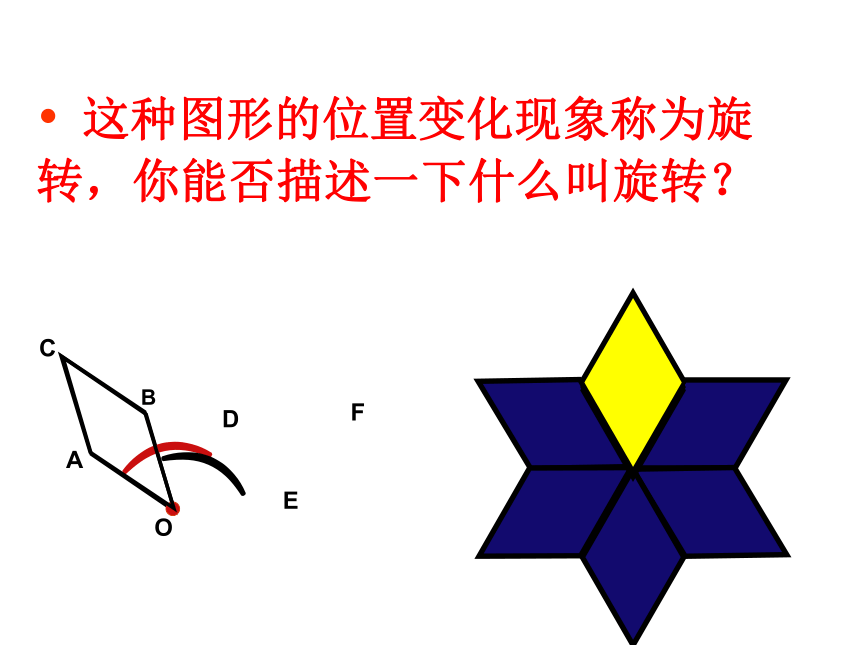
这种图形的位置变化现象称为旋转,你能否描述一下什么叫旋转?
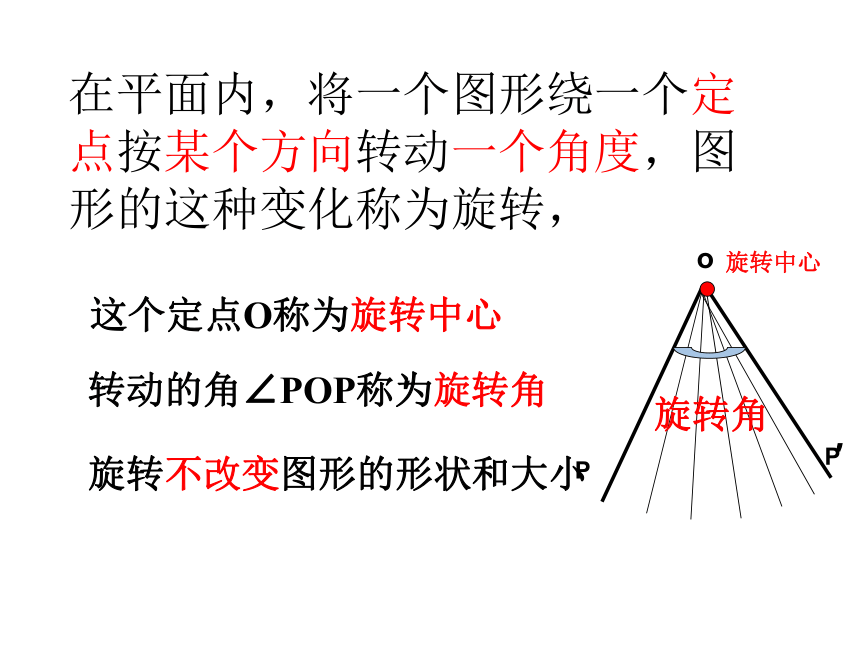
这个定点O称为旋转中心
旋转角
旋转中心
P
o
转动的角∠POP称为旋转角
P
′
′
在平面内,将一个图形绕一个定点按某个方向转动一个角度,图形的这种变化称为旋转,
旋转不改变图形的形状和大小
B
A
旋转的三要素
B
A
C
C
O
100
0
旋转中心
旋转角
旋转方向
旋转的三要素:
△ABC绕__点,沿___方向转动__度到△A’B’C’ .
O
顺时针
100
指出旋转中心、旋转方向、旋转角度
如图,如果把四边形AOBC绕着O点旋转得到四边形DOEF. 在这个旋转过程中:
⑴旋转中心是( )。
⑵经过旋转,点A和点B分别移动到( )的位置。
⑶旋转角是( )。
⑷AO与DO、 BO与EO的长度关系是
( )。
⑸∠AOD与∠BOE的
大小关系是( )
旋转中心是O
点D和点E
AO=DO;BO=EO
∠AOD=∠BOE
∠AOD和∠BOE
思考题
如图:△ABC是等边三角形,D是BC边上的一点,△ABD经过旋转后到达△ACE的位置 .
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB上
中点,那么经过上述
的旋转后,点M到了
什么位置?
B/
A/
A
B
C/
C
O
2.对应点到旋转中心的距离相等;
3.两组对应点分别与旋转中心的连线所成的角
相等
一个图形和它经过旋转所得到的图形中
1.旋转后的图形与原图形全等
旋转的性质:
例1 如图,如果把钟表的指针看作四边形AOBC,它绕O点按顺时针方向旋转得到四边形DOEF.在这个旋转过程中:
(1)旋转中心是什么 旋转角是什么
(2)经过旋转,点A,C, B分别移动到什么位置?
(3)AO 与 DO 的长有什么关系 还有其他相等的线段吗
(4)∠AOD与∠BOE有什么大小关系
A
O
C
D
F
E
B
◆什么叫图形的旋转?
◆图形旋转的性质是什么?
在平面内,将一个图形绕一个定点旋转一定的角度,这样的图形运动叫做图形的旋转.这个定点叫旋转中心.旋转的角度称为旋转角.
1.旋转前、后的图形全等.
2.对应点到旋转中心的距离相等.
3 .每一对对应点与旋转中心的连线所成的角彼此相等.
◆图形的旋转是由旋转中心和旋转的角度决定.
课堂小结
第四章 图形的平移与旋转
【学习目标】
1.通过对生活中与旋转现象有关的图形进行观察、分析,以及动手操作、画图等过程,掌握有关的画图技能。
2.通过具体实例认识旋转,理解旋转前后两个图形对应点到旋转中心距离相等,对应点与旋转中心的连线所成的角彼此相等的性质,发展初步的审美能力。
观察思考
F
︵
A
B
C
D
E
O
︵
这种图形的位置变化现象称为旋转,你能否描述一下什么叫旋转?
这个定点O称为旋转中心
旋转角
旋转中心
P
o
转动的角∠POP称为旋转角
P
′
′
在平面内,将一个图形绕一个定点按某个方向转动一个角度,图形的这种变化称为旋转,
旋转不改变图形的形状和大小
B
A
旋转的三要素
B
A
C
C
O
100
0
旋转中心
旋转角
旋转方向
旋转的三要素:
△ABC绕__点,沿___方向转动__度到△A’B’C’ .
O
顺时针
100
指出旋转中心、旋转方向、旋转角度
如图,如果把四边形AOBC绕着O点旋转得到四边形DOEF. 在这个旋转过程中:
⑴旋转中心是( )。
⑵经过旋转,点A和点B分别移动到( )的位置。
⑶旋转角是( )。
⑷AO与DO、 BO与EO的长度关系是
( )。
⑸∠AOD与∠BOE的
大小关系是( )
旋转中心是O
点D和点E
AO=DO;BO=EO
∠AOD=∠BOE
∠AOD和∠BOE
思考题
如图:△ABC是等边三角形,D是BC边上的一点,△ABD经过旋转后到达△ACE的位置 .
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB上
中点,那么经过上述
的旋转后,点M到了
什么位置?
B/
A/
A
B
C/
C
O
2.对应点到旋转中心的距离相等;
3.两组对应点分别与旋转中心的连线所成的角
相等
一个图形和它经过旋转所得到的图形中
1.旋转后的图形与原图形全等
旋转的性质:
例1 如图,如果把钟表的指针看作四边形AOBC,它绕O点按顺时针方向旋转得到四边形DOEF.在这个旋转过程中:
(1)旋转中心是什么 旋转角是什么
(2)经过旋转,点A,C, B分别移动到什么位置?
(3)AO 与 DO 的长有什么关系 还有其他相等的线段吗
(4)∠AOD与∠BOE有什么大小关系
A
O
C
D
F
E
B
◆什么叫图形的旋转?
◆图形旋转的性质是什么?
在平面内,将一个图形绕一个定点旋转一定的角度,这样的图形运动叫做图形的旋转.这个定点叫旋转中心.旋转的角度称为旋转角.
1.旋转前、后的图形全等.
2.对应点到旋转中心的距离相等.
3 .每一对对应点与旋转中心的连线所成的角彼此相等.
◆图形的旋转是由旋转中心和旋转的角度决定.
课堂小结
