人教版八年级下册 19.2.2一次函数课后巩固练习(含答案)
文档属性
| 名称 | 人教版八年级下册 19.2.2一次函数课后巩固练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 207.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-01 14:55:41 | ||
图片预览

文档简介
19.2.2 一次函数 课后巩固练习
一、单选题
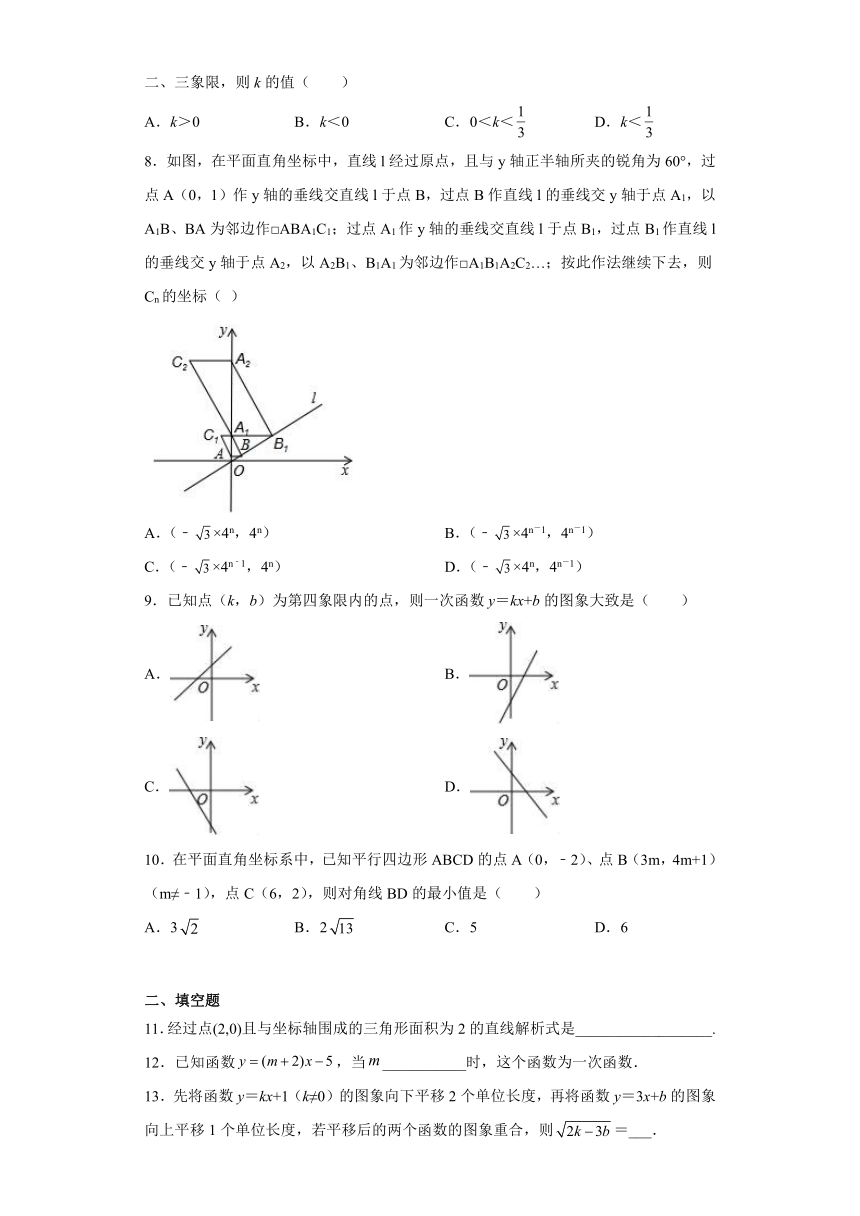
1.已知一次函数的图象经过点,则k的值是( )
A.1 B.0 C. D.4
2.正比例函数与一次函数在同一坐标系中的大致图像可能是( )
A. B.C. D.
3.两个一次函数和在同一平面直角坐标系中的图象可能是( )
A. B. C.D.
4.已知一次函数y=(k-2)x+k+1的图象不过第三象限,则k的取值范围是( )
A.-1≤k<2 B.-1≤k≤2 C.-15.已知 x 满足 5 x 6, x 1, 2x 4 ,对任意一个x ,m 都取,中的较小值,则 m 的最大值是( )
A.14 B.7 C.-4 D.2
6.下列关于一次函数的说法,错误的是( )
A.函数图象与y轴的交点 B.当x值增大时,y随着x的增大而减小
C.当时, D.图象经过第一、二、三象限
7.已知一次函数y=(1﹣3k)x+k的函数值y随x的增大而增大,且图象经过第一、二、三象限,则k的值( )
A.k>0 B.k<0 C.0<k< D.k<
8.如图,在平面直角坐标中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1,以A1B、BA为邻边作□ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1、B1A1为邻边作□A1B1A2C2…;按此作法继续下去,则Cn的坐标( )
A.(﹣×4n,4n) B.(﹣×4n-1,4n-1)
C.(﹣×4n﹣1,4n) D.(﹣×4n,4n-1)
9.已知点(k,b)为第四象限内的点,则一次函数y=kx+b的图象大致是( )
A. B.
C. D.
10.在平面直角坐标系中,已知平行四边形ABCD的点A(0,﹣2)、点B(3m,4m+1)(m≠﹣1),点C(6,2),则对角线BD的最小值是( )
A.3 B.2 C.5 D.6
二、填空题
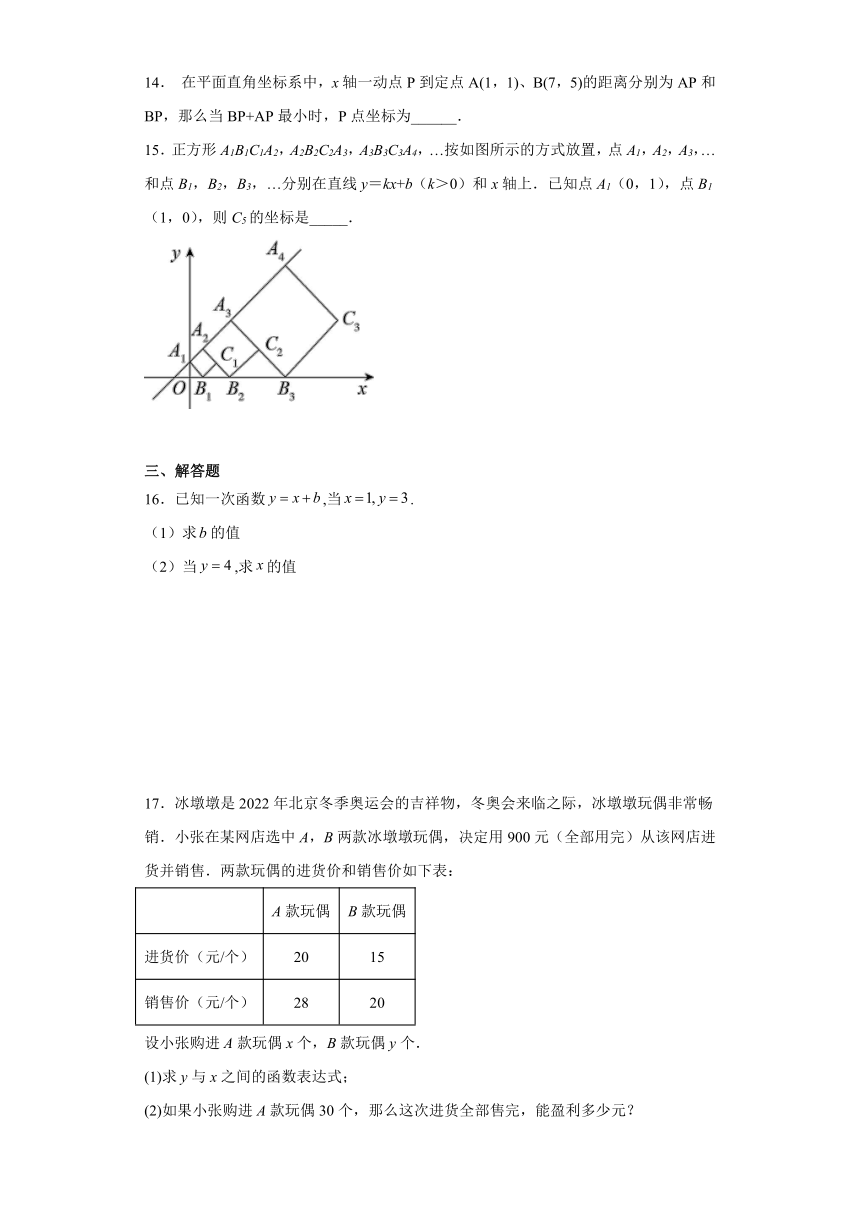
11.经过点(2,0)且与坐标轴围成的三角形面积为2的直线解析式是__________________.
12.已知函数,当___________时,这个函数为一次函数.
13.先将函数y=kx+1(k≠0)的图象向下平移2个单位长度,再将函数y=3x+b的图象向上平移1个单位长度,若平移后的两个函数的图象重合,则=___.
14. 在平面直角坐标系中,x轴一动点P到定点A(1,1)、B(7,5)的距离分别为AP和BP,那么当BP+AP最小时,P点坐标为______.
15.正方形A1B1C1A2,A2B2C2A3,A3B3C3A4,…按如图所示的方式放置,点A1,A2,A3,…和点B1,B2,B3,…分别在直线y=kx+b(k>0)和x轴上.已知点A1(0,1),点B1(1,0),则C5的坐标是_____.
三、解答题
16.已知一次函数,当.
(1)求的值
(2)当,求的值
17.冰墩墩是2022年北京冬季奥运会的吉祥物,冬奥会来临之际,冰墩墩玩偶非常畅销.小张在某网店选中A,B两款冰墩墩玩偶,决定用900元(全部用完)从该网店进货并销售.两款玩偶的进货价和销售价如下表:
A款玩偶 B款玩偶
进货价(元/个) 20 15
销售价(元/个) 28 20
设小张购进A款玩偶x个,B款玩偶y个.
(1)求y与x之间的函数表达式;
(2)如果小张购进A款玩偶30个,那么这次进货全部售完,能盈利多少元?
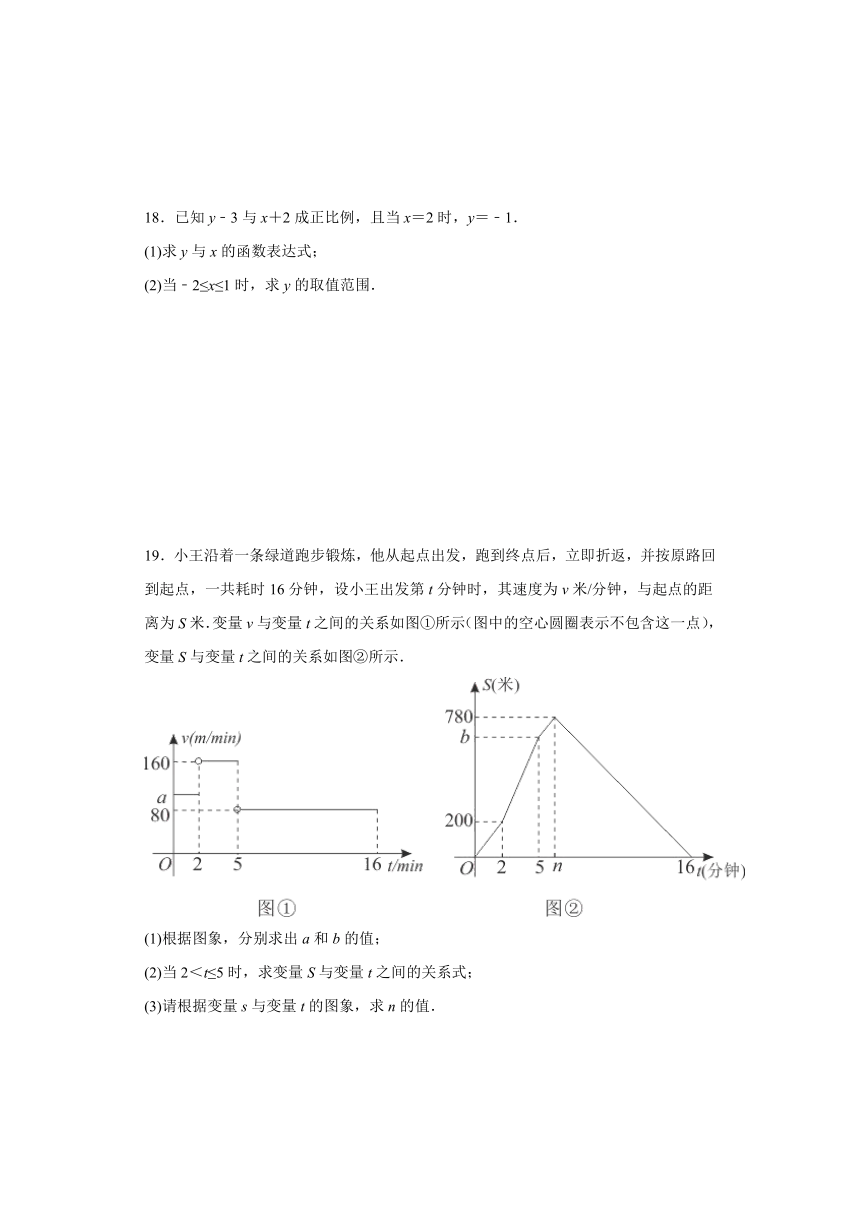
18.已知y﹣3与x+2成正比例,且当x=2时,y=﹣1.
(1)求y与x的函数表达式;
(2)当﹣2≤x≤1时,求y的取值范围.
19.小王沿着一条绿道跑步锻炼,他从起点出发,跑到终点后,立即折返,并按原路回到起点,一共耗时16分钟,设小王出发第t分钟时,其速度为v米/分钟,与起点的距离为S米.变量v与变量t之间的关系如图①所示(图中的空心圆圈表示不包含这一点),变量S与变量t之间的关系如图②所示.
(1)根据图象,分别求出a和b的值;
(2)当2<t≤5时,求变量S与变量t之间的关系式;
(3)请根据变量s与变量t的图象,求n的值.
20.如图,矩形ABCO中,点C在x轴上,点A在y轴上,点B的坐标是,矩形ABCO沿直线BD折叠,使A落在对角线OB上的点E处,折痕与OA、x轴分别交于点D、F.
(1)求线段BO的长;
(2)求直线BD的解析式;
(3)N为x轴上一动点,在点N运动的过程中,是否存在以EN为底边的等腰三角形OEN,若存在,直接写出点N的坐标;若不存在,请说明理由.
参考答案
1.A
2.D
3.B
4.A
5.D
6.D
7.C
8.C
9.B
10.D
11.y=x-2或y=-x+2
12.
13.
14.(2, 0)
15.(47,16)
16.解:(1)将x=1,y=3 代入y=x+b 中
即3=1+b 解得b=2
解析式为 y=x+2
(2)将y=4 代入解析式中
4=x+2 解得x=2
故答案为:(1)b=2(2)x=2
17.(1)解:由题意得:,
即.
(2)解:当时,,
则盈利为(元),
答:这次进货全部售完,能盈利340元.
18. (1)解:设正比例函数解析式为
将x=2,y=﹣1代入得
解得
∴可得y与x的函数表达式为.
(2)解:将代入,解得
将代入,解得
由的图象性质可知,当﹣2≤x≤1时,
∴y的取值范围为.
19 (1) , ,
所以 的值为100, 的值为680;
(2)当2<t≤5时,设变量S与变量t之间的关系式为 ,
将(2,200)、(5,680)代入得: ,解得 ,
即;
(3)由图像得: ,即n的值为.
20.(1)解:∵B(-6,8),
∴OC=6,BC=8,
∵四边形ABCO是矩形,
∴∠BCO=90°
由勾股定理得BO=;
(2)解:设D(0,b),则OD=b,
由题意得:∠DEO=90°,DA=DE=8-b,BE=BA=6,
∵OB=10,
∴EO=4,
在Rt△DEO中, ,
即,解得b=5,
所以D点坐标为(0,5),
设直线BD的解析式为y=kx+b,
把B(-6,8),D(0,5)代入y=kx+b得:
,解得:,
所以直线BD的解析式为:;
(3)解:存在以EN为底边的等腰三角形,
∵OE=4,ON=OE,
∴ON=4,
∴N点的坐标为(4,0)或(-4,0).
一、单选题
1.已知一次函数的图象经过点,则k的值是( )
A.1 B.0 C. D.4
2.正比例函数与一次函数在同一坐标系中的大致图像可能是( )
A. B.C. D.
3.两个一次函数和在同一平面直角坐标系中的图象可能是( )
A. B. C.D.
4.已知一次函数y=(k-2)x+k+1的图象不过第三象限,则k的取值范围是( )
A.-1≤k<2 B.-1≤k≤2 C.-1
A.14 B.7 C.-4 D.2
6.下列关于一次函数的说法,错误的是( )
A.函数图象与y轴的交点 B.当x值增大时,y随着x的增大而减小
C.当时, D.图象经过第一、二、三象限
7.已知一次函数y=(1﹣3k)x+k的函数值y随x的增大而增大,且图象经过第一、二、三象限,则k的值( )
A.k>0 B.k<0 C.0<k< D.k<
8.如图,在平面直角坐标中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1,以A1B、BA为邻边作□ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1、B1A1为邻边作□A1B1A2C2…;按此作法继续下去,则Cn的坐标( )
A.(﹣×4n,4n) B.(﹣×4n-1,4n-1)
C.(﹣×4n﹣1,4n) D.(﹣×4n,4n-1)
9.已知点(k,b)为第四象限内的点,则一次函数y=kx+b的图象大致是( )
A. B.
C. D.
10.在平面直角坐标系中,已知平行四边形ABCD的点A(0,﹣2)、点B(3m,4m+1)(m≠﹣1),点C(6,2),则对角线BD的最小值是( )
A.3 B.2 C.5 D.6
二、填空题
11.经过点(2,0)且与坐标轴围成的三角形面积为2的直线解析式是__________________.
12.已知函数,当___________时,这个函数为一次函数.
13.先将函数y=kx+1(k≠0)的图象向下平移2个单位长度,再将函数y=3x+b的图象向上平移1个单位长度,若平移后的两个函数的图象重合,则=___.
14. 在平面直角坐标系中,x轴一动点P到定点A(1,1)、B(7,5)的距离分别为AP和BP,那么当BP+AP最小时,P点坐标为______.
15.正方形A1B1C1A2,A2B2C2A3,A3B3C3A4,…按如图所示的方式放置,点A1,A2,A3,…和点B1,B2,B3,…分别在直线y=kx+b(k>0)和x轴上.已知点A1(0,1),点B1(1,0),则C5的坐标是_____.
三、解答题
16.已知一次函数,当.
(1)求的值
(2)当,求的值
17.冰墩墩是2022年北京冬季奥运会的吉祥物,冬奥会来临之际,冰墩墩玩偶非常畅销.小张在某网店选中A,B两款冰墩墩玩偶,决定用900元(全部用完)从该网店进货并销售.两款玩偶的进货价和销售价如下表:
A款玩偶 B款玩偶
进货价(元/个) 20 15
销售价(元/个) 28 20
设小张购进A款玩偶x个,B款玩偶y个.
(1)求y与x之间的函数表达式;
(2)如果小张购进A款玩偶30个,那么这次进货全部售完,能盈利多少元?
18.已知y﹣3与x+2成正比例,且当x=2时,y=﹣1.
(1)求y与x的函数表达式;
(2)当﹣2≤x≤1时,求y的取值范围.
19.小王沿着一条绿道跑步锻炼,他从起点出发,跑到终点后,立即折返,并按原路回到起点,一共耗时16分钟,设小王出发第t分钟时,其速度为v米/分钟,与起点的距离为S米.变量v与变量t之间的关系如图①所示(图中的空心圆圈表示不包含这一点),变量S与变量t之间的关系如图②所示.
(1)根据图象,分别求出a和b的值;
(2)当2<t≤5时,求变量S与变量t之间的关系式;
(3)请根据变量s与变量t的图象,求n的值.
20.如图,矩形ABCO中,点C在x轴上,点A在y轴上,点B的坐标是,矩形ABCO沿直线BD折叠,使A落在对角线OB上的点E处,折痕与OA、x轴分别交于点D、F.
(1)求线段BO的长;
(2)求直线BD的解析式;
(3)N为x轴上一动点,在点N运动的过程中,是否存在以EN为底边的等腰三角形OEN,若存在,直接写出点N的坐标;若不存在,请说明理由.
参考答案
1.A
2.D
3.B
4.A
5.D
6.D
7.C
8.C
9.B
10.D
11.y=x-2或y=-x+2
12.
13.
14.(2, 0)
15.(47,16)
16.解:(1)将x=1,y=3 代入y=x+b 中
即3=1+b 解得b=2
解析式为 y=x+2
(2)将y=4 代入解析式中
4=x+2 解得x=2
故答案为:(1)b=2(2)x=2
17.(1)解:由题意得:,
即.
(2)解:当时,,
则盈利为(元),
答:这次进货全部售完,能盈利340元.
18. (1)解:设正比例函数解析式为
将x=2,y=﹣1代入得
解得
∴可得y与x的函数表达式为.
(2)解:将代入,解得
将代入,解得
由的图象性质可知,当﹣2≤x≤1时,
∴y的取值范围为.
19 (1) , ,
所以 的值为100, 的值为680;
(2)当2<t≤5时,设变量S与变量t之间的关系式为 ,
将(2,200)、(5,680)代入得: ,解得 ,
即;
(3)由图像得: ,即n的值为.
20.(1)解:∵B(-6,8),
∴OC=6,BC=8,
∵四边形ABCO是矩形,
∴∠BCO=90°
由勾股定理得BO=;
(2)解:设D(0,b),则OD=b,
由题意得:∠DEO=90°,DA=DE=8-b,BE=BA=6,
∵OB=10,
∴EO=4,
在Rt△DEO中, ,
即,解得b=5,
所以D点坐标为(0,5),
设直线BD的解析式为y=kx+b,
把B(-6,8),D(0,5)代入y=kx+b得:
,解得:,
所以直线BD的解析式为:;
(3)解:存在以EN为底边的等腰三角形,
∵OE=4,ON=OE,
∴ON=4,
∴N点的坐标为(4,0)或(-4,0).
