12.2 完全平方公式（1）课件

课件27张PPT。第12章 乘法公式与因式分解 12.2完全平方公式
教学目标知识技能：解决问题：情感态度：知道完全平方公式与多项式乘法的关系，理解完全平方公式的意义。经历完全平方公式的探求过程，熟悉完全平方公式的特征，会运用完全平方公式解决一些简单问题。使学生体会数形结合的优势，进一步发展符号感和推理能力，培养学生数学建模的思想。鼓励学生自己探索算法的多样化，有意识地培养学生的创新能力。教学重点及难点难点：① 对公式中字母a、b的广泛含义的理解与正确应用。
② 正确、灵活地选用模型。 重点：体会完全平方公式的发现和推导过程，理解公式的本质，完全平方公式的结构特点及公式的直接运用。
?
?
⑴、分别写出每块实验田的面积；
⑵、用不同的形式表示实验田的总面积，并进行比较，你发现了什么？
1、想一想:
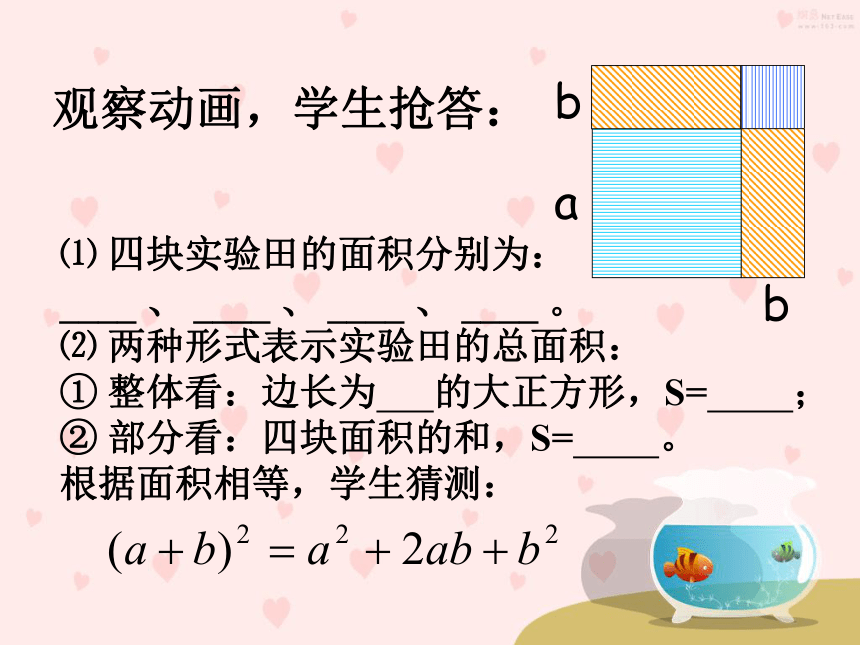
一块边长为a米的正方形实验田，因需要将其边长增加b米，形成四块实验田，以种植不同的新品种，（如图所示）
⑴ 四块实验田的面积分别为：
____ 、 ____ 、 ____ 、 ____ 。
⑵ 两种形式表示实验田的总面积：
① 整体看：边长为 的大正方形，S= ；
② 部分看：四块面积的和，S= 。
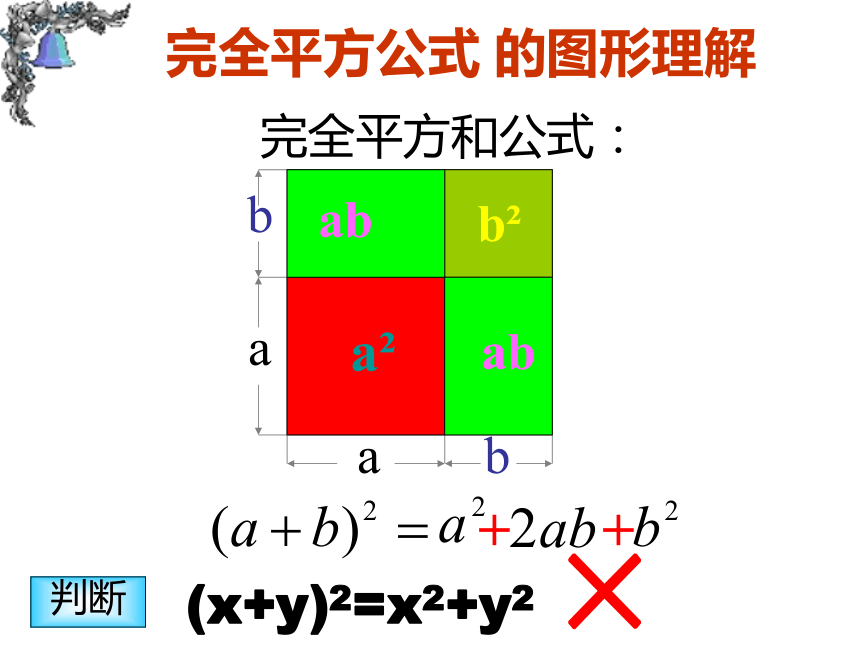
根据面积相等，学生猜测： 观察动画，学生抢答：(a+b)2a2b2完全平方和公式：完全平方公式 的图形理解×②3、做一做
你能利用面积知识，仿照课本以及演示的动画，用白纸折出
的示意图吗?
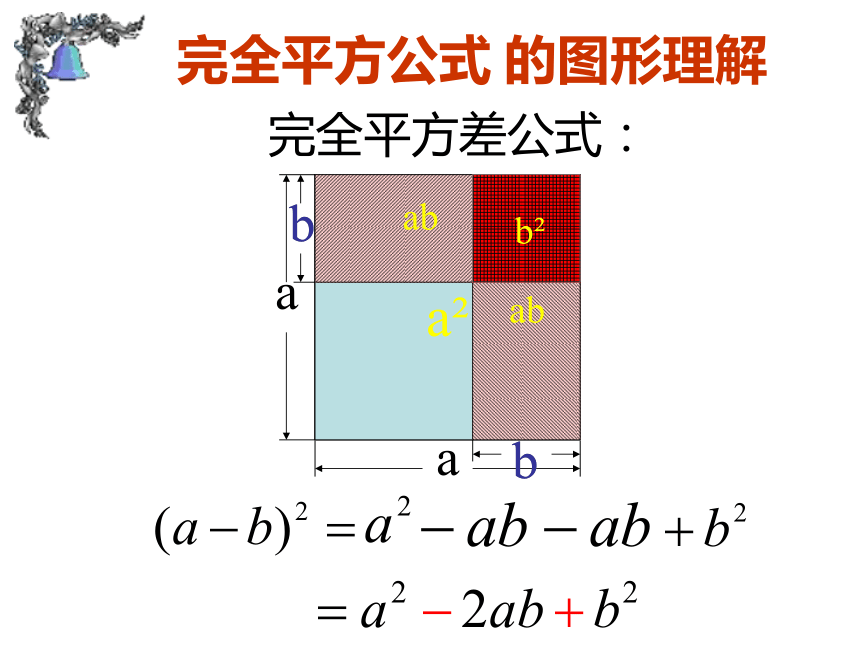
说明：学生分成2人一组动手折纸，并互相交流结果。 (a-b)2b2完全平方差公式：完全平方公式 的图形理解问题：①这两个公式有何相同点与不同点？
②你能用自己的语言叙述这两个公式吗？
学生4人一组讨论两个问题，填表：②、学生用语言叙述完全平方公式。公式特点：4、公式中的字母a，b可以表示数，单项式和
多项式。(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b21、积为二次三项式；2、积中两项为两数的平方和；3、另一项是两数积的2倍，且与乘式中
间的符号相同。首平方，末平方，首末两倍中间放 完全平方公式：(a+b)2= a2 +2ab+b2
(a+b)2= a2 +2ab+b2
语言表达：
两数和（差）的平方等于这两个数的平方和加上（减去）它们乘积的2倍。下面各式的计算是否正确？如果不正确，应当怎样改正？（口答）(x+y)2=x2 +y2(2)(x -y)2 =x2 -y2(3) (x -y)2 =x2+2xy +y2(4) (x+y)2 =x2 +xy +y2错错错错(x +y)2 =x2+2xy +y2(x -y)2 =x2 -2xy +y2(x -y)2 =x2 -2xy +y2(x +y)2 =x2+2xy +y2例1 运用完全平方公式计算：解： (x+2y)2==x2(1)(x+2y)2(a +b)2= a2 + 2 ab + b2x2+2?x ?2y+(2y)2+4xy+4y2解： (x-2y)2==x2(2)(x-2y)2(a - b)2= a2 - 2 ab + b2x2-2?x ?2y+(2y)2-4xy+4y21.(3x-7y)2 = 2.(2a2+3b)2= 算一算例2运用完全平方公式计算：(1) 1042解： 1042= (100+4)2=10000+800+16=10816(2) 99.992解： 99.992= (100 –0.01)2=10000 -2+0.0001=9998.00011192=8.92利用完全平方公式计算：=例3 计算：(1) ( a2 + b3)2解：原式= ( b3 a2)2= b6 - 2 a2 b3+ a4(a-b)2 =(b-a)2(2)(- x2y - )2解：原式= ( x2y + )2= x4y2 + x2y +(-a-b)2 =[-(a+b)]2 =(a+b)2(2) (a - b)2 与 (b - a)2
(-b +a)2 与(-a +b)2(1) (-a -b)2 与(a+b)2比较下列各式之间的关系：相等相等1.(-x-y)2 = 2.(-2a2+b)2= 你会了吗通过这节课的学习你学到了什么课堂小结：(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b21、完全平方公式：2、注意：项数、符号、字母及其指数；3、公式的逆向使用：4、解题时常用结论：(-a-b)2 =(a+b)2 (a-b)2 =(b-a)2a2 +2ab+b2 = (a+b)2
a2 - 2ab+b2= (a-b)2几点注意：1、项数：积的项数为三；2、符号：特别是(a-b)2= a2 - 2ab+b2；3、字母：不要漏写；4、字母指数：当公式中的a、b所代表的
单项式字母指数不是1时，乘方时要
记住字母指数需乘2。作业：
课本第117页习题12.2 第1、2题 谢
谢
再
见