(华东师大)第15章 图形的全等教案[上学期]
文档属性
| 名称 | (华东师大)第15章 图形的全等教案[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-23 22:41:00 | ||
图片预览


文档简介
24.1.1图形的全等
教学目标:
1、通过问题的解决,图形的实例,体验全等图形的形成,体会到如何直观地判别两个图形是全等图形,通过动手实验进一步掌握全等图形的概念,全等多边形的特征;
2、了解全等多边形、对应边、对应顶点、对应角的概念;
3、培养学生动手试验的能力与习惯,树立实践出真知的观念。
重点难点:
难点:全等多边形的概念和特征;
重点:全等多边形的对应元素的确定。
教学准备:
动员学生课堂上带剪刀、厚纸板。教师带照片几张。
教学过程:
一、复习引入
1、问题1、请同学们观察老师手上的两张照片(1寸和2寸的照片),用你们学过的知识来回答观察到什么?
(两张照片是相似图形,其相似比是)
2、请几位同学说说相似图形的特征与识别。
3、问题2:请同学们再观察老师手上的两张照片(都是两寸的照片),也用数学的知识说说观察到什么?
(两个图形的形状、大小也一样,即相似比的相似图形)
本节开始,我们就来探索、研究这种图----§24.1图形的全等
二、新授
1、全等图形
试一试:(课本P78)你能找到几对形状相同、大小一样的图形吗?
(两对:(2)和(4)、(3)和(6))
问:如何判断两个图形的大小和形状是否完全相同的?
(学生各抒已见,给予表扬鼓励;通过师生之间交流,得出全等图形的形状和
大小都相等)
问:发挥你们的想像,两个大小和形状完全相同的图形叠合在一起,是否完全重合。动手试试。
(可用你们带来的工具)
(完全重合)
问:通过动手试验,你得到了什么结论?
(判断两个图形的大小和形状是否完全相同,可以把两个图形叠合在一起,看是否完全重合。)
我们把能够完全重合的两个图形叫做全等形。
练习:(1)课本试一试的图中的 就是全等形。
(2)课本 P80 练习
2、全等多边形及对应顶点、对应边、对应角的概念。
问题3:观察老师的演示(用大小一样的照片,演示翻折、旋转、平移的运动),请问:老师把这些图形进行哪些运动?形状、大小发生了改变吗?从中你得到了什么结论?
学生发表看法。
老师总结:我们把图形的翻折、旋转、平移称是图形的三种基本的运动,图形经过这样的运动,位置虽然发生了变化,但形状、大小却没有改变,前后两个图形是全等的。反过来,两个全等的图形经过这样的运动一定能够重合。
完成课本P79 思考。
由学生的回答中引出:
全等多边形:能够完全重合的两个多边形。
对应顶点:两个全等的多边形,经过运动而重合,相互重合的顶点。
对应边:相互重合的边。
对应角:相互重合的角。
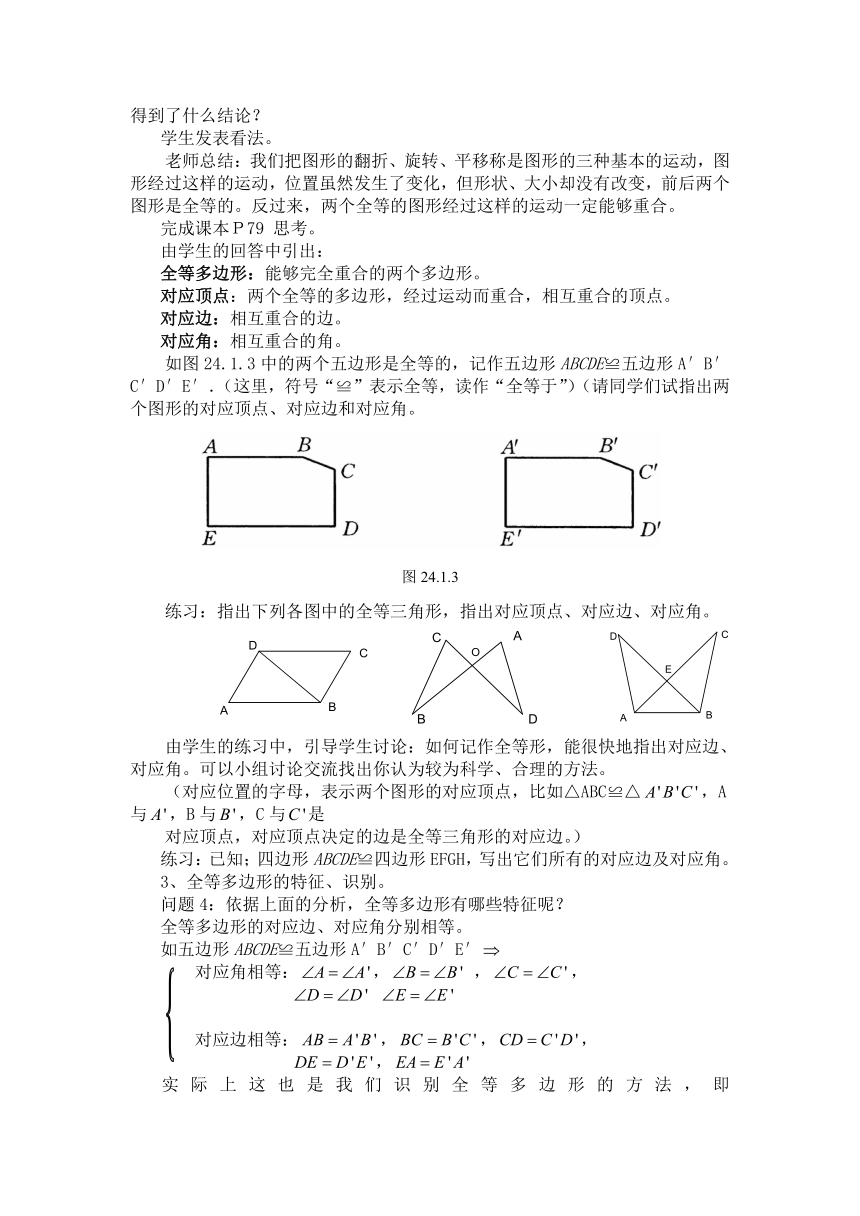
如图24.1.3中的两个五边形是全等的,记作五边形ABCDE≌五边形A′B′C′D′E′.(这里,符号“≌”表示全等,读作“全等于”)(请同学们试指出两个图形的对应顶点、对应边和对应角。
练习:指出下列各图中的全等三角形,指出对应顶点、对应边、对应角。
由学生的练习中,引导学生讨论:如何记作全等形,能很快地指出对应边、对应角。可以小组讨论交流找出你认为较为科学、合理的方法。
(对应位置的字母,表示两个图形的对应顶点,比如△ABC≌△,A与,B与,C与是
对应顶点,对应顶点决定的边是全等三角形的对应边。)
练习:已知;四边形ABCDE≌四边形EFGH,写出它们所有的对应边及对应角。
3、全等多边形的特征、识别。
问题4:依据上面的分析,全等多边形有哪些特征呢?
全等多边形的对应边、对应角分别相等。
如五边形ABCDE≌五边形A′B′C′D′E′
对应角相等:, ,,
对应边相等:,,,
,
实际上这也是我们识别全等多边形的方法,即__________________________________的两个多边形全等。
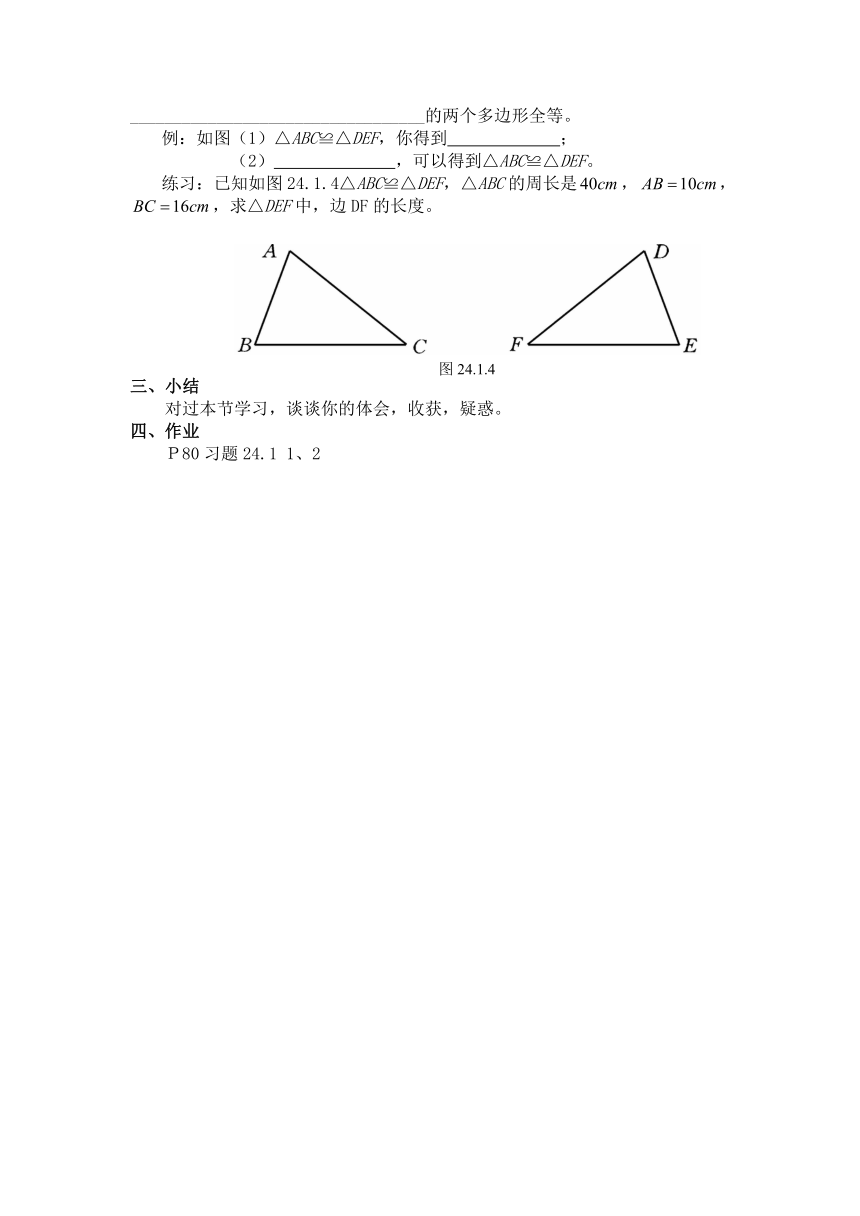
例:如图(1)△ABC≌△DEF,你得到 ;
(2) ,可以得到△ABC≌△DEF。
练习:已知如图24.1.4△ABC≌△DEF,△ABC的周长是,,,求△DEF中,边DF的长度。
三、小结
对过本节学习,谈谈你的体会,收获,疑惑。
四、作业
P80习题24.1 1、2
24.2.1全等三角形的识别(1)
教学目标:
1、经历探索三角形全等条件的过程,体会如何探索研究问题。培养学生合作的精神,让学生体验分类的思想;
2、使学生懂得如何提出问题,分类讨论,并为以后研究提出问题。
重点难点:
1、难点:培养学生探索问题能力;
2、重点:掌握探索问题的方法。
教学过程:
一、复习
1、请一位同学叙述上一节所学的知识。
2、如图,△ABC≌△AEC,,,求出△AEC各内角的度数。
3、你是如何来识别两个三角形全等的?
从学生的回答中,提出:我们能不能找到一些较为简便的方法用来识别三角形的全等呢?有没有类似于相似三角形的识别方法呢?
回想一下,相似三角形有哪些识别方法?
本节开始,我们就一起来研究,探讨§24.2全等三角形的识别。
二、新授
要画一个三角形与老师在黑板上画的三角形ABC全等,需要几个与边或角的大小有关的条件呢?一个条件、两个条件、三个条件……
1、做一做
(1)只给一个条件:一条边,大家画出三角形,小组交流画的三角形全等吗?一个角,大家画出三角形,小组交流画的三角形全等吗?
(2)给出两个条件画三角形时,有几种可能的情况?这两个三角形一定会全等吗?分别按照下面条件,用刻度尺或量角器画三角形,并和周围的同学比较一下,所画的图形是否全等。
①三角形的一个内角为60°,一条边为3 cm;
② 三角形的两个内角分别为30°和70°;
③ 三角形的两条边分别为3 cm和5 cm
你们在画图和同学比较过程中,你能得出什么结论?
学生各抒己见后,教师归纳:你们一定会发现,如果只知道两个三角形有一个或两个对应相等的部分(边或角),那么这两个三角形不一定全等(甚至形状都不相同)。
2、议一议
如果给出三个条件画三角形,你能说出有哪几种可能的情况?
(有四种可能:三条边、三个角、两边一角和两角一边)
对于按以上每一种可能画得三角形是否全等,以后我们一起分别逐个探讨研究,现在我们先一起来完成以下几个练习。
三、巩固练习
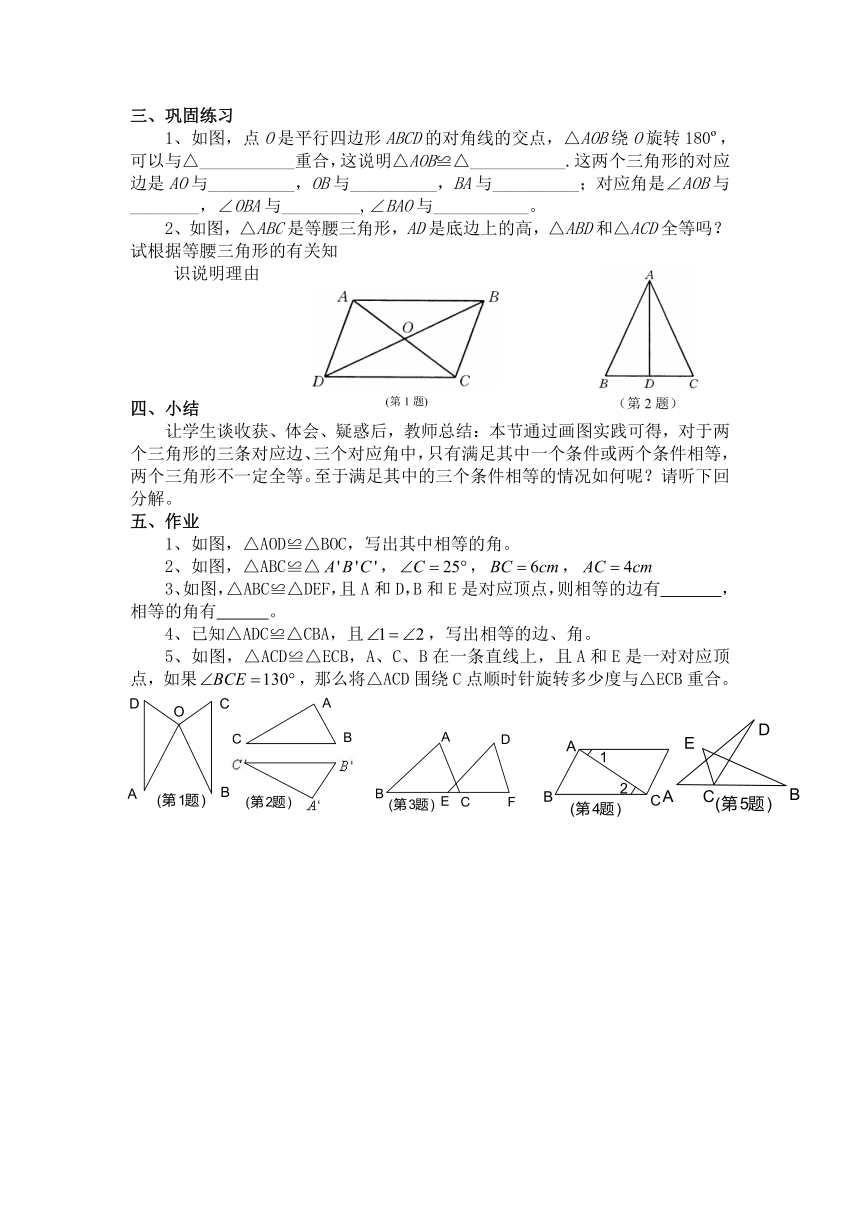
1、如图,点O是平行四边形ABCD的对角线的交点,△AOB绕O旋转180 ,可以与△___________重合,这说明△AOB≌△___________.这两个三角形的对应边是AO与__________,OB与__________,BA与__________;对应角是∠AOB与________,∠OBA与_________,∠BAO与___________。
2、如图,△ABC是等腰三角形,AD是底边上的高,△ABD和△ACD全等吗?试根据等腰三角形的有关知
识说明理由
四、小结
让学生谈收获、体会、疑惑后,教师总结:本节通过画图实践可得,对于两个三角形的三条对应边、三个对应角中,只有满足其中一个条件或两个条件相等,两个三角形不一定全等。至于满足其中的三个条件相等的情况如何呢?请听下回分解。
五、作业
1、如图,△AOD≌△BOC,写出其中相等的角。
2、如图,△ABC≌△,,,
3、如图,△ABC≌△DEF,且A和D,B和E是对应顶点,则相等的边有 ,相等的角有 。
4、已知△ADC≌△CBA,且,写出相等的边、角。
5、如图,△ACD≌△ECB,A、C、B在一条直线上,且A和E是一对对应顶点,如果,那么将△ACD围绕C点顺时针旋转多少度与△ECB重合。
24.2.2全等三角形的识别(2)
教学目标:
1、使学生理解边边边公理的内容,能运用边边边公理证明三角形全等,为证明线段相等或角相等创造条件;
2、继续培养学生画图、实验,发现新知识的能力。
重点难点:
难点:让学生掌握边边边公理的内容和运用公理的自觉性;
重点:灵活运用SSS识别两个三角形是否全等。
教学过程:
一、创设问题情境,引入新课
请问同学,老师在黑板上画得两个三角形,△ABC与△全等吗?你是如何识别的。
(同学们各抒己见,如:动手用纸摹下一个三角形,剪下叠到另一个三角形上,是否完全重合;测量两个三角形的所有边与角,观察是否有三条边对应相等,三个角对应相等。)
上一节课我们已经探讨了两个三角形只满足一个或两个边、角对应相等条件时,两个三角形不一定全等。满足三个条件时,两个三角形是否全等呢?现在,我们就一起来探讨研究。
二、实践探索,总结规律
1、问题1:如果两个三角形的三条边分别相等,那么这两个三角形会全等吗?
做一做:给你三条线段、、,分别为、、,你能画出这个三角形吗?
先请几位同学说说画图思路后,教师指导,同学们动手画,教师演示并叙述书写出步骤。
步骤:
(1)画一线段AB使它的长度等于c(4.8cm).
(2)以点A为圆心,以线段b(3cm)的长为半径画圆弧;以点B为圆心,以线段a(4cm)的长为半径画圆弧;两弧交于点C.
(3)连结AC、BC.
△ABC即为所求
把你画的三角形与其他同学的图形叠合在一起,你们会发现什么?
换三条线段,再试试看,是否有同样的结论
请你结合画图、对比,说说你发现了什么?
同学们各抒己见,教师总结:给定三条线段,如果它们能组成三角形,那么所画的三角形都是全等的。
这样我们就得到识别三角形全等的一种简便的方法: 如果两个三角形的三条边分别对应相等,那么这两个三角形全等.简写为“边边边”,或简记为(S.S.S.)。
2、问题2:你能用相似三角形的识别法解释这个(SSS)三角形全等的识别法吗?
(我们已经知道,三条边对应成比例的两个三角形相似,而相似比为1时,三条边就分别对应相等了,这两个三角形不但形状相同,而且大小都一样,即为全等三角形。)
3、问题3、你用这个“SSS”三角形全等的识别法解释三角形具有稳定性吗?
(只要三角形三边的长度确定了,这个三角形的形状和大小就完全确定了)
4、范例:
例1 如图24.2.2,四边形ABCD中,AD=BC,AB=DC,
试说明△ABC≌△CDA.
解:已知 AD=BC,AB=DC,
又因为AC是公共边,由(S.S.S.)
全等识别法,可知△ABC≌△CDA
5、练习:
P84 练习1、2
6、试一试:已知一个三角形的三个内角分别为、、,你能画出这个三角形吗?把你画的三角形与同伴画的进行比较,你发现了什么?
(所画出的三角形都是相似的,但大小不一定相同)。
三个对应角相等的两个三角形不一定全等。
三、加强练习,巩固知识
1、如图,,,△ABC≌△DCB全等吗?为什么?
2、如图,AD是△ABC的中线,。与相等吗?请说明理由。
四、小结
本节课探讨出可用(SSS)来识别两个三角形全等,并能灵活运用(SSS)来识别三角形全等。三个角对应相等的两个三角不一定会全等。
五、作业
P90习题24.2 1
24.2.3全等三角形的识别(3)
教学目标:
1、使学生掌握SAS的内容,会运用SAS来识别两个三角形全等;
2、通过识别全等三角形的识别的学习,使学生初步认识事物之间的因果关系与相互制约关系,学习分析事物本质的方法;
3、经历如何总结出全等三角形识别方法,体会如何探讨、实践、总结,培养学生的合作能力。
重点难点:
1、难点:三角形全等的识别:SAS;
2、重点:对全等三角形的识别的理解和运用。
教学过程:
一、复习
1、什么叫全等图形?什么叫做全等三角形?
(能够完全重合的两个图形叫做全等形,能够完全重合的两个三角形叫做全等三角形)。
2、将全等的△ABC与△DEF重合,再沿BC方向将△DEF推移如图位置,问线段AD与BE数量关系怎样?BC与EF位置关系怎样?为什么?
解: ,BC∥EF
∵ △ABC≌△DEF
∴
∴
∴
又∵ △ABC≌△DEF
∴
∴ BC∥EF ]
(虽然本教材没有采用∵∴的形式,但根据《课标》的精神,结合其他版本教材,如北师大的版本,建议可以采用,可以使解题简捷。)
3、已知:如图,,,,,求的大小。
解:,,
∴ △ACB≌△AED
∴
∴
∴
∴]
二、新授
1、引入;上一节课,我们已经知道两个三角形满足三个条件的三条边对应相等和三个角对应相等的情况。情况如何呢?
(三条边对应相等两个三角形;三个角对应相等的两个三角形不一定全等)
如果两个三角形有两条边和一个角分别对应相等,这两个三角形会全等吗?-------这就是本节课我们要探讨的课题。
2、问题1:如果已知一个三角形的两边及一角,那么有几种可能的情况呢?
(应该有两种情况:一种是角夹在两条边的中间,形成两边夹一角;另一情况是角不夹在两边的中间,形成两边一对角。)
每一种情况下得到的三角形都全等吗?
3、做一做
(1)如果“两边及一角”条件中的角是两边的夹角,比如三角形两条边分别为和,它们的夹角为,你能画出这个三角形吗?你画的与同伴画的一定全等吗?
换两条线段和一个角试试,你发现了什么?
同学们各抒己见后总结:发现对于已知的两条线段和一个角,以该角为夹角,所画的三角形都是全等的。
这就是判别三角形全等的另外一种简便的方法:
如果两个三角形有两边及其夹角分别对应相等,那么这两个三角形全等.简写成“边角边”或简记为(S.A.S.)
你能用相似三角形的识别法来解释这种“SAS”识别三角形全等的方法吗?
(一个角对应相等而夹这个角的两边对应成比例的两个三角形相似,当相似比为1时,夹这个角的两
边对应相等,这两个三角形的形状、大小都相同,即为全等三角形)
(2)如果“两边及一角”条件中的角是其中一边的对角,比如两条边分别为和,长度为的边所对的角为,情况会怎样呢
请画出这个三角形,把你画的三角形与其他同学画的三角形进行比较,由此你发现了什么?
(两边及其中一边的对角对应相等,两个三角形不一定全等。)
4、范例:如图,△ABC中,AB=AC,AD平分∠BAC,试说明△ABD≌△ACD.
解 已知 AB=AC,∠BAD=∠CAD,
又AD为公共边,由(S.A.S.)全等识别法,可知
△ABD≌△ACD
三、巩固练习
P86 练习1、2
四、小结
学生谈收获、体会、疑惑后,进一步总结本节学习了三角形全等的识别的另一种SAS,而两边及其中一边的对角对应相等的两个三角形不一定全等,注意观察图形的特征,找出是否具备满足两个三角形全等的条件。
五、作业
P90 习题24.2 2
24.2.4全等三角形的识别(4)
教学目标:
1、使学生理解ASA的内容,能运用ASA全等识别法来识别三角形全等进而说明线段或角相等;
2、通过画图、实验、发现、应用的过程教学,树立学生知识源于实践用于实践的观念。使学生体会探索发现问题的过程。经历自己探索出AAS的三角形全等识别及其应用。
重点难点:
难点:三角形全等的识别法ASA和AAS及应用;
重点:利用三角形全等的识别法,间接说明角相等或线段相等。
重点难点:
剪刀、卡纸。
教学过程:
一、复习
1、什么叫做全等三角形,如何识别两个三角形全等?
(能够完全重合的两个三角形叫做全等三角形。识别两个三角形全等的方法有:SSS;SAS)。
2、叙述SSS、SAS的内容。
3、已知:如图,,,请问再加上什么条件下,△ABC≌△,并说明理由。
(,根据SSS;,根据SAS)。
二、新授
1、引入:请问到本节为止,我们探讨两个三角形满足三个条件的哪几种情况,情况如何呢?
(如果两个三角形有三条边分别对应相等或两个三角形有两条边及其夹角分别对应相等,那么这两个三角形就一定全等。如果两个三角形有三个角分别对应相等,或两个三角形的两边及其一边所对的角对应相等,那么这两个三角形不一定全等。)
还有哪些情况还没有探讨呢?
(如果两个三角形的两个角及一条边分别对应相等,这两个三角形一定全等吗?)
本节我们闵来探讨两个三角形的两个角及一条边分别对应相等,这两个三角形是否全等的课题。
2、问题1:如果把已知一个三角形的两角及一边,那么有几种可能的情况呢?
(一种情况是两个角及两角的夹边;另一种情况是两个角及其中一角的对边。)
每一种情况下得到的三角形都全等吗?
3、请同学们动手做一个实验:同桌两位同学为一组。
(1)共同商定画出任意一条线段AB,与两个角、()
(2)两位同学各自在硬纸板上画线段的长等于商定的线段AB的长,在的同旁,画等于商定的,画等于商定的,设与相交于,便得△。
(3)用剪刀各自剪出△,将同桌同学剪出的两个三角形重叠在一起发现了什么?其他各桌的同学是否也有同样的结论呢?
同学们各抒己见后,总结:对于已知两个角和一条线段,以该线段为夹边,所画的三角形都是全等的.
由此得到另一个识别全等三角形的简便方法:
如果两个三角形的两个角及其夹边分别对应相等,那么这两个三角形全等.简记为“角边角”或简记为(A.S.A.)。
4、问题2:试说明ASA全等识别法与相似三角形的识别法有什么类似的。
(两个角对应相等的两个三角形相似,当这两个角的公共边相等时,这两个三角形的形状、大小都相同,即为全等三角形。)
5、思考:如图,如果两个三角形有两个角及其中一个角的对边分别对应相等,
那么这两个三角形是否一定全等?
动手画一画:比如,,,你能画这个三角形吗?
提示:这里的条件与实验中的条件有什么相同点与不同点?你能将它转化为实验中的条件吗?
你画的三角形与同伴画的一定全等吗?
现在两组同学按如果角所对的边为画,另两组同学换两个角和一条线段,试试看,你们得出什么结论?
同学们各抒己见后,总结:对于已知两个角和一条线段,以该线段为夹边,所画的三角形都是全等的.
由此得到另一个识别全等三角形的简便方法:
如果两个三角形的两个角及其夹边分别对应相等,那么这两个三角形全等.简写成:“角角边”或简记为(A.S.A.)。
6、问题3:你能说说ASA与AAS这两种全等识别法间的关系吗?
(AAS识别法可由ASA识别法推导出来,如上图中,因为,,由于,,所以,于是△ABC与△DEF具备ASA全等。)
7、范例
如图,,,试说明△ABC≌△DCB
解:已知,
又BC是公共边,由(ASA)全等识别法,
可知△ABC≌△DCB
三、巩固练习
P88练习 1、2
四、小结
用采访的形式访问一些同学,本节学到什么知识,对这些知识有什么体会,对本节的知识存在着哪些疑问。
五、作业
P90习题24.2 3、4、5
24.2.5全等三角形的识别(5)
教学目标:
1、帮助学生总结一般三角形全等的识别条件,使他们自觉运用各种全等识别法进行说理;
2、通过一般三角形全等识别条件的归纳,帮助学生认识事物间存在着的因果关系和制约的关系。
重点难点:
重点:让学生识别三角的哪些元素能用来确定三角形的形状与大小,因而可用来识别三角形全等。
难点:灵活应用各种识别法识别全等三角形。
教学准备:
卡纸剪出的图1、2中的六个三角形。
I II I III
III II
(图1) (图2)
教学过程:
一、复习
1、识别两个三角形全等的条件有哪些?
(有SAS、ASA、AAS、SSS四种)
2、一个三角形共有三条边与三个角,你是否想到这样一问题了:除了上述四种识别法,还有其他的三角形全等识别法吗?比如说“SSA”、“AAA”能成为判定两个三角形全等的条件吗?
二、新授
1、演示
(1)演示图1中的I、II三角形,它们间有两边及一对角对应相等,这两个三角形能完全重合,是全等形。但再取出III的三角形与I叠在一起后,发现它们不重合不是全等形,因此我们进一点证实了:有两边和其中一边的对角对应相等的两个三角形不一定全等。“SSA”不是识别三角形全等的方法。
(2)演示图2中的I、II三角形,它们间有三个角对应相等,这两个三角形能完全重合,是全等形,但再取出III的三角形与I叠在一起后,发现它们不重合,不是全等形。因此我们进一步证实了:三个角对应相等的两个三角形不一定全等“AAA”也不是识别三角形全等的方法。
2、填下表(挂出小黑板,让学生思考、讨论,共同填答)。
两个三角形中对应相等的元素 两个三角形是否全等 依据的识别法 反例
SSS √ SSS
SAS √ SAS
SSA X 可举反例
ASA √ ASA
AAS √ AAS
AAA X 可举反例
3、范例
例:如图,,,点F是CD的中点,吗?试说明理由。
教学要点:
(1)分析题目结论假定,可转化为,需证它们所在的两个三角形全等;
(2)观察图形,、中,并不在三角形中,为此添辅助线AC、AD;
(3)在△ACF与△ADF中,已知AF是公共边,CF=FD,尚缺一条件,它只能是AC与AD相等;
(4)为证AC与AD相等。又要找它们分别在的△ACB与△ADE;
(5)△ACB与△ADE,由已知条件可由SAS证它们全等;
(6)书写范例。
解:连结AC、AD,由已知AB=AE,,BC=DE
由SAS三角形全等识别法可知:
△ABC≌△AED
根据全等三角形的对应相等可知
由,,(公共边),
根据SSS可知△ACF≌△ADF
根据全等三角形的对应角相等可知
又由于F在直线CD上,可得,即。
你们可有其他方法吗?
三、巩固练习
1、如图,在△ABC中,,,试说明△AED是等腰三角形。
2、如图,AB∥CD,AD∥BC,与,与相等吗?说明理由。
四、小结
由学生对本节的学习过程进行总结。
五、作业
(一)、填空题:
1、有一边对应相等的两个 三角形全等;
2、有一边和 对应相等的两个三角形全等;
3、有两边和 一角对应相等的两个三角形全等;
4、如图,AB∥CD,AD∥BC,AC、BD相交于点O。
(1)由AD∥BC,可得 = ,由AB∥CD,可得 = ,又由 ,于是△ABD≌△CDB;
(2)由 ,可得AD=CB,由 ,可得△AOD≌△COB;
(3)图中全等三角形共有 对。
(二)、选择题:
1、若△ABC≌△BAD,A和B、C和D是对应顶点,如果,,,则BC的长是( )
A、 B、 C、 D、无法确定
2、下列各说法中,正确的是( )
A、有两边和一角对应相等的两个三角形全等;
B、有两个角对应相等且周长相等的两个三角形全等;
C、两个锐角对应相等的两个直角三角形全等;
D、有两组边相等且周长相等的两个三角形全等。
(三)、解答题:
1、如图,,,AC、BD交于点
,图中共有几对长度相等的线段,
你是通过什么办法找到的?
2、如图,,,
(1)等于多少度?
(2)图中有哪几组平行线?
(3)与的和是定值吗?
24.2.6全等三角形的识别(6)
教学目标:
1、经历探索直角三角形全等条件的过程,掌握直角三角形全等的条件,并能运用其解决一些实际问题;
2、学习事物的特殊、一般关系、发展逻辑思维能力。
重点难点:
重点:让学生掌握直角三角形全等的“HL”识别法;
难点:理解直角三角形为内角在构造三角形时特殊性,并能灵活地运用各种全等识别法识别两个直角三角形全等是否全等。
教学准备:
剪刀、卡纸。
教学过程:
一、复习
如图,△ABC和△都是直角三角形,请你用所学的知识,须加上什么条件直角△ABC和△全等。并说明理由。
[,,(SAS);
,(ASA);
,,,(SSS)
,(AAS)]
等,让学生抢答。
二、创设问题情境
问题:舞台背景的形状是两个直角三角形。工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆计划遮住无法测量。
1、你能帮他想个办法吗?
2、如果他只带了一个卷尺,能完成这个任务吗?
[问题1,学生可以回答去量斜边和一锐角,或直角边和一个锐角;但对于问题2,学生则难肯定]。
工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”,你相信他的结论吗?
三、动手实践,探索新知
试以两条线段,,分别为直角边和斜边在卡纸上画一个三角形。
按照下面的步骤做一做:
(1)作;
(2)在射线CM上截取线段;
(3)以A为圆心,以长为半径画弧,交射线CN于点B;
(4)连结AB。
问: (1)△ABC就是所求作的三角形吗?(是的)
(2)剪下这个三角形,和其他同学所作的三角形进行比较,它们能重合吗?你发现了什么?
(能重合;发现:两个直角三角形的斜边及一条直角边分别对应相等,那么这两个直角三角形全等)
(3)你能用所学的知识来解决你的发现吗?
(由勾股定理可知,另一条直角边也是对应相等的)
因此可以得到如下结论:
如果两个直角三角形的斜边及一条直角边分别对应相等,那么这两个直角三角形全等. 简记为(H.L.)
四、想一想
你可以用几种方法说明两个直角三角形全等?
五、例题
如图24.2.13,AB是圆O的直径,AC=AD,试说明△ABC和△ABD全等.
解:因为AB为⊙O的直径,所以
∠ACB=∠ADB=90°.
又 AC=AD,AB=AB,
由(H.L.)全等识别法,可知
△ABC≌△ABD
六、巩固练习
P89 练习1、2
七、小结
学生谈谈收获、疑惑。总结本节学习直角三角形全等的识别,除了一般三角形全等识别法外,还有“HL”。
八、作业
P90 习题24.2 6
24.3.1定义、命题与定理
教学目标:
1、了解定义、命题、真命题、假命题、定理的含义,会区分命题的条件(题设)和结论,奠定推理论证的基础;
2、初步体会合理化思想,使学生明确什么定理及其意义。
重点难点:
1、重点:定义、命题、公理、定理的概念;
2、难点:判定什么定义、命题、定理、公理,及找出命题的题设和结论。
教学过程:
一、创设问题情境引入
情境1:小亮和小刚正在津津有味地阅读《我们爱科学》。
小亮:“哈!这个黑客终于被逮住了。”
小刚:“是的,现在英特网广泛运用于我们的生活中,给我带来了方便,但……”
坐在旁边的两个人一边听着他的谈话,一边也在悄悄议论着。
“这个黑客是个小偷吗?”
“可能是喜欢穿黑衣服的贼。”
“那因特网肯定是一张很大的网。”
“估计可能是英国造的特殊的网。”
你听完这则片段故事,有何想法?
同学们各抒己见后,老师给予同学的各种回答评价后,发表自己的看法:在日常生活中,我们会遇到许多概念,假如不对这些概念下定义,别人就无法理解这引起概念,以致无法进行正常的交流。同样,在数学学习中,要进行严格的论证,也必须首先对所涉及的概念下定义。本节我们就一起来学习——§24.3命题与证明的第一节定义、命题与定理。
练习:课本P93 练习1
二、共同探索获得新知
1、试一试:得出定义
你是如何找出图中的平行四边形呢?
“有两组对边分别平行的四边形叫做平行四边形”这句话说明了平行四边形的含义以及区别于其他图形的特征。
一般地,能明确指出概念含义或特征的句子,称为定义。
例如:(1) 有一个角是直角的三角形,叫做直角三角形.
(2) 有六条边的多边形,叫做六边形.
(3) 在同一平面内,两条不相交的直线叫做平行线.
你还能举出一些其他的例子吗?
观察这些定义,你发现定义中用词有什么特征?
同学们各抒己见后,总结:定义必须是严密的.一般避免使用含糊不清的术语,比如“一些”、“大概”、
“差不多”等不能在定义中出现.正确的定义能把被定义的事物或名词与其他的事物或名词区别开来。
2、思考:得出命题
思考:试判断下列句子是否正确。
(1)如果两个角是对顶角,那么这两个角相等;
(2)三角形的内角和是180°;
(3)同位角相等;
(4)平行四边形的对角线相等;
(5)菱形的对角线相互垂直
根据已有的知识可以判断出句子(1)、(2)、(5)是正确的,句子(3)、(4)是错误的.像这样可以
判断它是正确的或是错误的句子叫做命题(proposition).正确的命题称为真命题,错误的命题称为假命题。
练习:
(1)下列句子哪些是命题?
①动物都需要水;
②猴子是动物的一种;
③玫瑰花是动物;
④美丽的天空;
⑤对应角都相等的两个三角形一定全等;
⑥负数都小于零;
⑦你的作业做完了吗?
⑧所有的质数都是奇数;
⑨过直线外一点作l的平行线;
⑩如果,,那么。
(2)练习:课本P93 练习3
3、观察发现,命题结构。
观察下列命题,你能发现这些命题有什么共同的结构特征?与同样交流。
(1)如果两个三角形的三条边相等,那么这两个三角形全等;
(2)如果一个三角形是等腰三角形,那么这个三角形的两个底角相等;
(3)如果一个四边形的对角线相等,那么这个四边形是矩形;
(4)如果一个四边形的一组对边平行且相等,那么这个四边形是平行四边形;
(5)如果一个四边形的两条对角线互相垂直,那么这个四边形是菱形。
总结:在数学中,许多命题是由题设(或条件)和结论两部分组成的.题设是已知事项,结论是由已知事项推出的事项.这种命题常可写成“如果……那么……”的形式.其中,用“如果”开始的部分是题设,用“那么”开始的部分是结论.例如,在命题(1)中,“两个角是对顶角”是题设,“这两个角相等”是结论。
例、把命题“在一个三角形中,等角对等边”改写成“如果……那么……”的形式,并分别指出命题的题设与结论.
解:这个命题可以写成:“如果在一个三角形中有两个角相等,那么这两个角所对的边也相等.” 这里的题设是“在一个三角形中有两个角相等”,结论是“这两个角所对的边也相等”。
练习:课本P93 练习2
4、追溯根源:明确定理
问题:如何证实一个命题是真命题呢?
用我们以前学过的观察、实践、验证特例等方法。这些方法往往并不可靠。
能不能根据已经知道的真的命题证实呢?那已知知道的真命题又是如何证实呢?
哦……那可怎么办?
其实,在数学发展史上,数学家们也遇到类似的问题。公元前3世纪,人们已经积累了大量的数学知识,在此基础上,古希腊数学家欧几里得编写了一本书,书名叫《原本》。为了说明每一个结论的正确性,他在编写这本书时进行了大胆创造:挑战了一部分数学名词和一部分公认的真命题作为证实其他命题的起始依据,其中数学名词称为原名,公认的真命题称为公理。即数学中有些命题的正确性是人们在长期实践中总结出来的,并把它们作为判断其他命题真假的原始依据,这样的真命题叫做公理。
小组竞赛:
请你说出学过知识中,哪些是公理,哪组说的又多又准就是获胜者。
如:
(1)一条直线截两条平行直线所得的同位角相等;
(2)两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行;
(3)如果两个三角形的两边及其夹角(或两角及其夹边,或三边)分别对应相等,那么这两个三角形全等;
(4)全等三角形的对应边、对应角分别相等
此外,我们把等式、不等式的有关性质以及等量代换(即在等式或不等式中,一个量用它的等量替代)都作为逻辑推理的依据.
有些命题可以从公理或其他真命题出发,用逻辑推理的方法判断它们是正确的,并且可以进一步作为判断其他命题真假的依据,这样的真命题叫做定理(theorem).
例如,运用公理“两角及其夹边分别对应相等的两个三角形全等”,可以得到定理:“两角及其一角的对边分别对应相等的两个三角形全等.”
男女对抗赛:由男女同学各说定理,并分别由对方判断正误,说对一个定理得1分,高分都获胜。
三、巩固知识、归纳总结
同学们,本节你学到了哪些知识?有何体会?还有什么疑惑呢?若同学有疑惑,还可一起讨论,帮助解惑。
四、作业
P93 习题24.3 1、2
24.3.2证明(1)
教学目标:
1、初步了解证明意义及基本步骤和书写格式;
2、感受几何中推理的严谨、结论的确定;
3、体验举反例说明命题是假命题。
重点难点:
1、重点:证明的基本步骤和书写格式;
2、难点:几何中的逻辑推理。
教学过程:
一、复习
问题1:一位同学在钻研数学题时发现:
2+1=3,
2×3+1=7,
2×3×5+1=31,
2×3×5×7+1=211
于是,他根据上面的结果并利用素数表得出结论: 从素数2开始,排在前面的任意多个素数的乘积加1一定也是素数.他的结论正确吗?
计算一下,你发现什么?
问题2:如图所示,一个同学在画图时发现: 三角形三条边的垂直平分线的交点都在三角形的内部。于是他得出结论: 任何一个三角形三条边的垂直平分线的交点都在三角形的内部.他的结论正确吗?
画一个钝角三角形试试看。
问题3:我们曾经通过计算四边形、五边形、六边形、七边形、八边形等的内角和,得到一个结论: n边形的内角和等于(n-2)×180°.这个结果可靠吗?是否有一个多边形的内角和不满足这一规律?
问题4:以上3个问题的解决中,你有何体会呢?
上面几个例子说明: 通过特殊的事例得到的结论可能正确,也可能不正确.因此,通过这种方式得到的结论,还需进一步加以证实。
本节就来学习解决此问题的知识-------证明。
二、新授
1、证明的概念
根据题设、定义以及公理、定理等,经过逻辑推理,来判断一个命题是否正确,这样的推理过程叫做证明。
2、证明一个命题是真命题
(1)前面的学习已经告诉我们:一条直线截两条平行线所得的内错角相等.下面我们运用前面所提到的基本事实,即公理来证明这个结论.
例1 证明: 一条直线截两条平行直线所得的内错角相等.
已知: 如图24.3.3,直线l1∥l2,直线l3分别和l1、l2相交于点A、B.
求证: ∠1=∠3.
证明: 因为 l1∥l2(已知),
所以 ∠1=∠2 (两直线平行,同位角相等).
又 ∠2=∠3 (对顶角相等),
所以 ∠1=∠3 (等量代换)
(2)总结
观察老师的范例你有何体会?
同学们各抒已见后,总结证明一下命题是真命题的步骤:
①根据命题画出图形,标上字母;
②结合图形写出已知、求证;
③有题设、定义以及公理、定理等,经过逻辑推理,得出正确的结论。
(3)练习
①课本P96 练习1;
②证明:同旁内角互补,两直线平行。
证明一个命题是假命题
如果要证明或判断一个命题是假命题,怎么办呢?
(1)范例
例,证明“一个锐角与一个钝角的和等于一个平角”是假命题,只要举出一个符合命题题设而不符合结论的例子就可以了,这称为“举反例”。
解:例如锐角等于30°,钝角等于120°,但它们的和就不等于180°,从而说明这个命题是假命题。
(2)练习
①课本P96 练习2
②举反例说明“一个数的绝对值大于这个数的本身。”是个假命题。
三、小结
本节学习了什么是证明,以及如何证明一个命题是真命题及假命题。特别是证明一个命题是真命题时,要注意须画出图形,写出已知、求证,并用逻辑推理出正确的结论。
四、作业
P97 习题24.3 3
课题 :24.3.3证明(2)
教学目标:
1、进一步理解和总结证明的步骤、格式和方法;
2、让学生在动口、动手、动脑的实践,直接经验、自己活动中获取知识,培养了学生的发散思考。
重点难点:
重点:掌握证明的步骤、格式和方法;
难点:熟练地证明。
教学过程:
一、复习引入
1、什么是证明?
(根据题设、定义以及公理、定理等,经过逻辑推理,来判断一个命题是否正确,这样的推理过程叫做证明)
2、如何证明一个命题是假命题?
(证明或判断一个命题是假命题,那么我们只要举出一个符合命题题设而不符合结论的例子就可以了)
3、你是如何证明了一个命题是真命题呢?
同学们各抒己见,我们今天这一节课继续来对所表述的结论是正确的通过推理的方式给予证明。
二、新授
1、范例1
例:内错角相等,两直线平行.
已知:如图24.3.4,直线l3分别交l1、l2于点A、点B,∠1=∠2.
求证: l1∥l2.
证明 因为 ∠1=∠2 (已知)
∠1=∠3 (对顶角相等)
所以 ∠2=∠3 (等量代换)
所以 l1∥l2 (同位角相等,两直线平行)
与你上节完成课时作业设计中此题的过程进行对比,你有何感受?请你对证明步骤进行总结,并与同伴交流。
证明步骤的一种可供参考的说法是:
(1)理解题意;
(2)根据题意正确画出图形;
(3)根据题意写出“已知”和“求证”;
(4)分析题意,探索证明的思路;
(5)依据寻求的思路,运用数学符号和数学语言条理清晰地写出证明过程;
(6)检查表达过程是否正确、完善。
2、范例2
例:已知:如图24.3.5,AB和CD相交于点O,∠A=∠B.
求证: ∠C=∠D
证明: 因为 ∠A=∠B(已知)
所以 AC∥BD (内错角相等,两直线平行)
所以 ∠C=∠D (两直线平行,内错角相等)
三、试一试
请在下面题目证明中的括号内填入适当的理由.
已知:如图24.3.6,AD=BC,CE∥DF,CE=DF.
求证: ∠E=∠F.
证明: 因为 CE∥DF ( ),
所以 ∠1=∠2 ( ).
在△AFD和△BEC中,因为
DF=CE ( ),
∠1=∠2 ( ),
AD=BC ( ),
所以 △AFD≌△BEC ( ),
所以 ∠E=∠F ( ).
四、巩固练习
1、已知:如图,直线AB、CD被EF、GH所截,∠1=∠2,求证:∠3=∠4.
2、已知:如图,AB=AC, ∠BAO=∠CAO.求证:OB=OC
五、小结
学生谈谈收获、疑惑。
八、作业
P97 习题24.3 4、5、6
课题 :24.4.1 尺规作图(1)画线段
教学目标:
1、会用尺规作一条线段等于已知线段;
2、明白尺规作图的意义和历史,并激发学生的学习兴趣。
重点难点:
重点:用尺规作一条线段等于已知线段;
难点:灵活地运用“作一线段等于已知线段”进行作图。
教学过程:
一、追溯根源,激发兴趣
你可以很容易地用量角器和刻度尺画一条线段等于已知线段,画一个角等于已知角.但如果限定使用的工具只能是圆规和没有刻度的直尺,即尺规作图,你还能画出符合条件的图形吗?
为什么对几何图要作出只用尺规作用的限制?
自古希腊时代起,人们就已经创造了尺规作图的游戏,这是一个十分有趣的游戏,吸引着许多人去探索。希腊人认为,几何的基本原则是只用极少的定义、公理推导出尽可能多的命题,因此作图的工具也要限制到不能再少的程度。希腊人还认为,学几何是为了训练思维,靠人去思考,而不是靠作图工具。因此,就规定了作图只能使用直尺和圆规这两种最简单的工具。
希腊的平面几何学(也就是现在世界通行的平面几何学)的作图方法规定:直尺无刻度,它的用法是经过两点可以作一直线;可以无限制地延长一直线。圆规的用法是以任意给定的点为中心,以任意给定的长为半径,可以作圆或画弧。用圆规、直尺作图时只能有限次使用圆规和直尺。此外还规定对于直线与直线、直线与圆(或弧)、圆(或弧)与圆(或弧)相交可以求它们的交点,这一整套的规定也称为平面几何作图公法。
对直尺和圆规能作出哪些图形以及不可能作出哪些图形的思考,竟推动了不整个数学的发展。本节开始,我们就来一起学习-----§24.4 尺规作图。本节就从最基本的图形开始-----画线段。
1、 试一试
如图24.4.1,MN为已知线段,你能用直尺和圆规准确地画一条与MN相等的线段吗?
你是如何画图呢?与同伴进行交流,请一些同学展示其成果。
作法:
(1)如图24.4.2,画射线AB,
(2)在射线AB上截取AC=MN(即:用圆规量出线段MN的长,以点A为圆心,以MN的长为半径画弧,交射线AB于点C。)
所以,线段AC就是所要画的线段.
三、做一做
如图,已知线段和两条互相垂直的直线AB、CD。
(1)利用圆规,在射线OA、OB、OC、OD上作线段、、、,使它们分别与线段相等;
(2)依次连接、、、、。
你得到了一个怎样的图形?与同伴交流。
[作图时,要求学生能口头表述作法,并能正确作出图形(保留作图痕迹),作出图形应为正方形。]
四、练一练
1、如图,已知线段和,直线AB、CD垂直且相交于O。
利用尺规,按下列要求作图:
(1)在射线OA、OB、OC上作线段、、,使它们分别与线段相等;
(2)在射线OD上作线段,使等于;
(3)依次连接、、、、。
你得到了一个怎样的图形?与同伴交流。
2、已知线段、和,求作:线段,使;
3、课本P100 练习1
五、说一说
(1)本节你学到了什么?
(2)你是如何用尺规画一条线段的?
(3)通过本节的学习,你有何体会?
六、作业
P103 习题24.4 1
课题 :24.4.2 尺规作图(2)画角
教学目标:
1、使学生掌握一个角等于已知角的基本作图;;
2、初步训练学生用规范的语言叙述尺规作图的动作,达到作图准确,叙述正确;
3、灵活运用画一个角的尺规作图,画一些其他图形。
重点难点:
重点:掌握用尺规画一个角及灵活运用画一个角在画其他图形中的使用;
难点:画图的几何语言叙述。
教学过程:
一、创设问题情境,激发学生兴趣
问题:如图,要在长方形木板截一个平行四边形,使它的一组对边在长方形木板的边缘上,另一组对边中的一条边为AB。
1、请过C点画出与AB平行的另一条边;
2、如果你只有一个圆规和一把没有刻度的直尺能解决这个问题吗?
你想如何处理此问题?
分析:要在长方形木板上截一个平行四边形,按图的方式(平行四边形的一组对边在长方形的边缘上),只要保证过点C作出与AB平行的另一条线段即可。而要过点C作AB的平行线,可以通过作一个角等于即可。
本节我们就来一起学习用尺规作一个角等于已知角。
二、试一试
图24.4.3,∠AOB为已知角,按下列步骤用圆规和直尺准确地画一个角等于∠AOB.
1、画射线O′A′;
2、以点O为圆心,以适当长为半径画弧,交OA于C,交OB于D;
3、以点O′为圆心,以OC长为半径画弧,交O′A′于C′.;
4、以点C′为圆心,以CD长为半径画弧,交前一条弧于D′;
5、经过点D′画射线O′B′;
所以,∠A′O′B′就是所要画的角。
用量角器验证你作的角与已知角是否相等。
(相等)
你能用所学的知识说明其中的理由吗?
(因为在作图过程知道:,,,所以△COD≌△,根据全等三角形对应角相等,可知。)
三、练一练
1、利用尺规完成本节课开始提出的问题。
2、已知,利用尺规作,使
3、课本P100 练习2
四、做一做
请你利用直尺和圆规分别画出满足图24.4.4和图24.4.5中条件的三角形ABC.
1、已知两边及夹角;
(不写画法,保留作图痕迹)
学生讨论后,教师示范。边叙述画法边画,学生跟着画。
(1)作;
(2)在射线BM上截取;
(3)在射线BN上截取;
(4)连结AC。
所以,△ABC就是所画的三角形。
还有其他的画法吗?动手试一试。
(如,先线段,画,在射线BM上截取,连结AC,即得△ABC)。
你从画图得到了什么?
同学们各抒己见。
(观察一个图形是由几个点确定了,能否画出这些点,若能,就可画出这个图形,若不能,就无法画出这个图形,为了便于分析,可画出草图)。
2、已知两角及夹边.
画完后,同学相互交流,指出对方的不足,或向对方提出问题,并请同学上板演示。
五、说一说
1、你本节学到了什么?
2、在你所学的知识中重点是什么?
3、在你所学的知识中注意什么?
4、你在本节的学习过程有何想法?
六、作业
P103 习题24.4 2、3
课题 :24.4.3 尺规作图(3)画垂线
教学目标:
1、使学生掌握作线段的垂直平分线,过一点作已知直线垂线的两种基本作图;
2、继续训练学生用简练、准确地运用几何语言表达作图方法与步骤,认识它的正确性、合理性;
3、培养学生探索问题、解决问题的方法,经历如何画线段的垂直平分线,体验利用画线段垂直平分线的方法为基础,画过一点作已知垂线的作图。
重点难点:
重点:让学生掌握过一点作直线的垂线,作直线的垂直平分线的基本方法;
难点:理解作图的理论依据。
教学过程:
一、复习
1、什么叫做尺规作图?
(限定用直尺和圆规来画图,称为尺规作图)
2、用尺规作图
(1)作线段,使它等于已知线段的长;
(2)作角,使它等于已知角;
①让学生在练习本上画任意长的线段和任意角。
②提问学生口述作法,教师在黑板上操作尺规画图,或教师口述作图步骤,让学生按老师的口述,操作尺规作图。
作线段:已知线段,作射线AC,以A为圆心,在AC上截取,AB就是所求作的;
作角:已知,作射线,以O为圆心,以任意长为半径作弧,分别交OA、OB于D、C两点,以为圆心,以OC为半径作弧,交于,以点为圆心,以CD长为半径作弧,交前弧于,经过作射线,就是所求的角。
3、什么垂直平分线?
(过线段的中点,垂直这条线段的直线)
4、线段垂直平分线有哪些特征?
(线段的垂直平分线上的点到线段两端点的距离相等;反过来,到线段两端点距离相等的点在线段的垂直平分线上)
二、做一做
如图,如图24.4.6,已知线段AB,画出它的垂直平分线.
提示:由线段垂直平分线的特征能否为你提供一些作图的依据。
若有学生懂得画,请他上台展示;若讨论没有结果的话,教师示范。
作法:1、分别以A、B两点为圆心,以大于长为半径画弧,两弧相交于C、D两点;
2、过C、D两点作直线CD。
所以,直线CD就是所求作的。
三、议一议
能否说出这种画法的依据,小组讨论交流。并发表小组的共识。
我们知道,线段的垂直平分线上的点到线段两端点的距离相等;反过来,到线段两端点距离相等的点在线段的垂直平分线上,因此如果能找到两个到线段两点的距离相等的点,那么过这两点就可画线段的垂直平分线。
如图,以点A为圆心,以大于AB一半的长为半径,在AB的一侧画弧; 以点B为圆心,以同样的长为半径,在AB的同一侧画弧,两弧的交点记为C,则C是线段AB垂直平分线上的一点.请你利用类似的方法确定另一点D。
因为画图可知AC=BC,所以点C在线段AB的垂直平分线上;又AD=BD,所以点D也在线段AB的垂直平分线上;根据两点确定一条直线,所以直线CD就是线段AB的垂直平分线。
四、试一试
1、如图,点C在直线上,试过点C画出直线的垂线。
提示:能否利用画线段垂直平分线的方法解决呢?
请同学们把你的作法在小组内交流,请一些同学上台展示其画图过程、画图的作法,并说明画图的依据。
作法:
(1)以C为圆心,任一线段的长为半径画弧,交l于A、B两点;
(2)分别以A、B两点为圆心,以大于长为半径画弧,两弧相交于C、D两点;
(3)过C、D两点作直线CD。
所以,直线CD就是所求作的。
理由:以C为圆心,任一线段的长为半径画弧,交l于A、B两点,则C是线段AB的中点.因此,过C画直线l的垂线转化为画线段AB的垂直平分线。
2、如图,如果点C不在直线上,试和同学讨论,应采取怎样的步骤,过点C画出直线的垂线?
请同学们把讨论结果上台展示。
作法:
(1)任取一点M,使点M和点C在的两侧;
(2)以C点为圆心,以CM长为半径画弧,交于A、B两点;
(3)分别以A、B两点为圆心,以大于长为半径画弧,两弧相交于D点;
(4)过C、D两点作直线CD。
所以,直线CD就是所求作的。
你能否用所学的知识证明这个结论呢?试试看。
证明:连结CA、CB、DA、DB,设CD、AB相交于O。
由作法知,,,CD是公共边,
所以△CAD≌△CBD(SSS)
所以(全等三角形的对应角相等)
于是△ACO≌△BCO(SAS)
所以AO=BO,(全等三角形的对应边、对应角相等)
所以CD是线段AB的垂直平分线。
五、练一练
P102 练习1、2
六、说一说
1、本节你有何收获?
2、本节你有何体会?
3、本节你有何疑惑?
七、作业
P103 习题24.6 4、5
课题 :24.4.4 尺规作图(4)画角平分线
教学目标:
1、使学生掌握画角平分线的作法;
2、进一步训练学生用规范的语言叙述尺规作图的动作,达到作图准确,叙述正确;
3、掌握利用基本作图作一些其他图形。
重点难点:
重点:让学生掌握画角平分线的作法;
难点:利用基本作图画一些其他图形。
教学过程:
一、复习
1、尺规作图的工具是 ;
2、尺规作图时,直尺的作用是画 、 、 ,圆规的作用是画圆的 ;
3、看图填空。
(1)在 上截取 = = ;
(2)以 为圆心,以 为半径作弧,交 于 。
(3)分别以 、 为圆心,以大于的长为半径作弧,两弧交于 、 ;
(4)以O为圆心,以任意为半径作弧,分别交的两边OA、OB于 、 。
(1) (2) (3) (4)
4、填空:
(1)求作一个角等于已知角,
作法:(1)作 ;
(2)以O为圆心,以 作弧,交 ;交 ;
(3)以为圆心,以 作弧,交 ;
(4)以 为圆心,以 半径作弧,交 ;
(5)经过 作 。则 即为所求的角。
5、如图,△ABC中,为钝角,求作:AB上的高CD。
作法:(1)以 为圆心,适当长为半径作弧交直线AB于 ;
(2)分别以 为圆心,大于 的长为半径作弧,两弧相交于 ;
(3) 作直线交AB于 ,则CD为所求的高。
6、求作线段MN的垂直平分线。
作法:(1) 为圆心, 为半径作弧,两弧相交于 ;
(2)作 AB;
则 线段MN的垂直平分线。
二、新授
1、做一做:利用直尺和圆规把一个角二等分。
观察右图,所画的射线OC是的角平分线,你能根据图中的作图痕迹,你能画一个角的角平分线并写出画图步骤吗?动手试试。
请一些同学上台展示成果。
作法:(1)以O点为圆心,以任意长为半径,交角的两边于A、B两点;
(2)分别以A、B两点为圆心,以大于长为半径画弧,画弧交于C点;
(3)过C点作射线OC。
所以,射线OC就是所求作的。
问:你能用所学的知识来说明所画的射线OC是的角平分线吗?小组里交流讨论后发表看法。
因为由画图可知:,,OC又是公共边,
根据三角形全等的识别(SSS),可得△OBC≌△OAC,
由全等三角形的对应边相等、对应角相等可知:
于是OC是的角平分线。
2、试一试:试把右图所示的角四等分
请完成操作写出画法。小组里相互交流,老师巡视。
三、巩固练习
课本P103 练习1、2
四、联系知识综合运用
1、范例
已知:两条线段、
求作:直角三角形ABC使直角的平分线等于,一直角边
分析:要想用尺规画出满足条件的图形,首先画出草图,从草图可知,△ADB可以确定,而C点是在过A点垂直AB的直线上,又在BD的延长线上,所以其交点就是C点,那么就确定了△ABC。
作法:(1)画线段AB;
(2)过A点作;
(3)作的角平分线AN;
(4)在射线AN上截取;
(5)连结BD并延长交射线AM于C点;
△ABC就是所求作的。
请你说说对这种画图方法,你是如何理解的。
2、练习
已知:角,线段。
求作:等腰三角形△ABC,使其顶角,平分线。
五、说一说
说说本节你的收获、体会、疑惑。
六、作业
P103 习题24.4 5
课题 :24.5.1 回顾与思考(1)
教学目标:
1、梳理所学的知识,进一步体会图形全等以及三角形全等的特征与识别;
2、进一步培养学生的知识分类能力、观察图形能力;
3、掌握有关的识别和特征,熟练地应用于判断、计算和说理。
重点难点:
重点:熟练地应用三角形的识别和特征进行有关的计算与说理;
难点:进行严密地推理。
教学过程:
一、说一说
1、对于§24.1--§24.2你学了哪些知识,并把这些知识理清。请一些同学说说见解。
知识结构图供参考
2、什么是全等图形?
3、全等图形的识别的方法是什么?
4、全等图形的特征是什么?
5、三角形全等有什么特征?
6、如何识别两个三角形全等?
7、如何识别两个直角三角形全等?
二、体会
1、体会读图、分析图形的能力。
问题1:如图,你能找到几个三角形?如果△AED≌△BEC,那么
它们的对应边、对应角是什么?这时图中还有没有其他全等三角形?
(有五个三角形,如果△AED≌△BEC,那么△DAB≌△CBA)
问题2:连结C、D两点,添了一条线段又多了多少个三角形呢?又有多少全等三角形呢?
问题3:观察下列图形,说说哪些三角形可能全等?
做完这些问题后有何体会?
(1)有公共边的两个三角形可能全等。
(2)有公共角或对顶角的两个三角形也可能全等。
2、体会分析
问题4:如图,AB=AC,D、E分别在AB、AC上,BC、CD相交于O,,试说明BD=CE。
分析:(1)
(2)
(3)△ADC≌△AEB
你能否把老师的分析用图表的形式来表示出来吗?
3、体会推理论证和书写过程。
请同学把上题的分析过程书写出来,你有何体会呢?
(通过三角形全等,可以得到线段和角的相等,有的题目通过说明一对三角形全等就可以得出结论,而有的题目,为了说明一对三角形全等,还要说明另一对三角形全等。)
三、做一做
1、如图,要识别△ABC≌△ADE,除公共角外,把还需要的两个条件及其根据写在横线上。
(1) , (SAS)
(2) , ( )
(3) , ( )
(4) , ( )
(5) , ( )
(6) , ( )
(7) , ( )
2、如图,D为BC中点,,且,与相等吗?为什么?
3、如图,AB=AC,BD、CE是△ABC的角平分线,△ABD≌△CBE吗?为什么?
4、如图,AB=AD,AC=AE,,△ABC与△ADE全等吗?
四、小结
通过本节学习,你有何体会?
五、作业
P106 复习题1、2、3、4
课题 :24.5.2 回顾与思考(2)
教学目标:
1梳理知识,掌握定义、命题、定理、公理与证明、尺规作图的基本知识和基本技能,培养主动参与、合作交流、进一步提高分析、概括能力;
2、能灵活运用所学的知识,进一步拓展知识。
重点难点:
重点:梳理知识、巩固基本知识和基本技能;
难点:灵活运用所学知识解决问题。
教学过程:
一、说一说,梳理本章知识
1、理清§24.3--§24.4的知识。
命题与证明定义、命题、公理证明
2、男、女生竞赛
男、女生轮流回答下列问题,相互指导,回答正确与指导有意义一次各10分,分数高者胜,按男、女顺序回答,回答不来1人次扣2分。
(1)什么是定义?
(2)什么命题?
(3)什么是公理?
(4)什么是定理?
(5)什么是证明?
(6)上台画线段等于已知线段。
(7)画角等于已知角。
(8)画一条直线的垂线。
(9)画一条线段的垂直平分线。
(10)画一个角的角平分线。
二、做一做,拓展知识
1、下列语句是命题吗?
(1)画一个角等于两个已知角的和;
(2)钝角总大于直角;
(3)过点A作直线AB∥CD;
(4)相等并且互补的两个角是直角。
2、判断下列命题是真命题还是假命题,若假命题,则举一个反例说明:
(1)两直线平行,同旁内角互补;
(2)垂直于同一条直线的两直线平行;
(3)相等的角是内错角;
(4)有一个角是的三角形是等边三角形。
3、命题“互补的角互为邻补角”,写成如果 ,那么 。
4、已知:如图,,AE=AD,求证:AB=AC。
5、两个直角三角形有一个角及一条边分别对应相等,这两个直角三角形全等吗?试列出各种情况,并一一加以分析。
6、(1)用直尺作法有:
①过点 ,点 ,作直线 ;
②连结两点
③延长 到点 ;
④延长 到点 ,使 = 。
(2)用圆规作法有:
①在 上截取 = ;
②以点 为圆心 为半径作弧;
③以点 为圆心 为半径作弧交 于点 ;
④分别以点 ,点 为圆心 为半径作弧,两弧交于点 。
(3)用到基本作图时:
①作线段 = ;
②作 = ;
③作射线 平分 ;
④过点 作 ⊥ ,垂足是 ;
⑤作线段 的垂直平分线。
试着画一个四边形,使它的面积等于已知三角形的面积的2倍,并写出画法。
三、小结
谈谈本节你有何收获。
四、作业
复习题7、8、9、10单元测试
一、填空题:
1、如图,已知AF∥EC,AB∥CD,∠A=70°,则∠C= 度。
(1) (2)
2. 如图:已知BE∥CF,∴∠2=∠3( );又 ∵∠1=∠4(已知),
∴∠1+∠2=∠3+∠4,即∠ABC=∠DCB∴ AB ∥CD( )
3. 如图, AB=AC,∠1=∠2,AD=AE,则BD= ,∠BAE= °
(3) (4)
4.若AB∥CD,∠A=35°,∠C=45°,则∠E= 度。(过E作AB的平行线)。
5. 如图,已知∠AFE=∠ABC,DG∥BE,∠DGB=130°,则∠FEB= 度。
(5) (6) (7)
6.已知点B、A、D在同一直线上,AE∥BC,∠1=150°,∠c=70°,则∠B= 度,
∠2= 度。
7. 如图,直线AB、CD被EF所截,已知∠1=∠2,求证:AB∥CD。
证明:∵∠2=∠3,( ),∠1=∠2(已知) ∴ ∠1=∠3∴ AB∥CD( ) 8.①、命题“对顶角相等”,改写成“如果……,那么……”的形式: 。题设是 ,结论是 。
②、两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行,
题设是 ;结论是 。
③、等角的补角相等,题设是 ,结论是 。
9、如图,直线AB上有一点O,过O点作射线OD、OC、OE,且OC、OE分别是∠BOD和∠AOD的平分线,则∠1与∠2的大小关系是 ,∠1+∠3= 度,OC与OE的位置关系是 。
10. 如图,ΔABC中,AB=AC=4,P是BC上任意一点,过P作PD⊥AC于D,PE⊥AB于E,若SΔABC=6,则PE+PD= 。
(9) (10) (11)
11、如图,已知∠ACB=∠BDA=90°,要使△ACB≌△BDA,至少还需加上条件: 。
12、如图, △ABC≌△ADE,∠B=35°,∠EAB=21°,∠C=29°,则∠D= ° ,∠DAC= °
13、如图、在正方形网格上有一个ΔABC,①、作一个与它全等的三角形。②、如每一个小正方形的边长为1,则ΔABC的面积是:
二、选择题:
1、下列给出的四组条件中,能判定△ABC≌△DEF的是( ).
A.AB=DE,BC=EF, ∠A=∠D; B.∠A=∠D, ∠C=∠F,AC=EF;
C.∠A=∠D,∠B=∠E,∠C=∠F;
D、AB=DE, BC=EF, △ABC周长=△DEF周长
2.如图,D在AB上,E在AC上,且∠B=∠C,那么补充
下列一个条件后,仍无法判定△ABE≌△ACD的是( ).
A.AD=AE. B.∠AEB=∠ADC. C.BE=CD. D.AB=AC.
3. 若△ABC≌△DEF,且△ABC的周长为20,AB=5,BC=8,则DF长为( ).
A.5; B.8; C.7; C.5或8.
4. 下列各条件中,不能作出唯一三角形的条件是( )
A. 已知两边和夹角 B. 已知两边和其中一条边所对的角
C. 已知两角和夹边 D. 已知两角和其中一角的对边
5. 求作点P,使P到三角形三边的距离相等的方法是( )
A. 作两边的中垂线的交点 B. 作两边上的高线的交点
C. 作两边上的中线的交点 D. 作两角平分线的交点
6. 命题① 邻补角互补;② 对顶角相等;③ 同旁内角互补;④ 两点之间线段最短;⑤直线都相等⑥任何数都有倒数;⑦若,则;⑧ 三角对应相等的两三角形全等 ⑨ 若∠A+∠A=90°,则∠A与∠B互余
其中真命题有( )
A. 1个 B. 2个 C. 3个 D. 4个
7、 有三条直线,若,,则与的位置关系( )
A. 平行 B. 垂直 C. 相交 D. 不确定
8、 两个角的两边分别平行,那么这两个角( )
A. 相等 B. 互补 C. 互余 D. 相等或互补
9、下列语句中:① 同角的补角相等;② 雪是白的;③ 画∠AOB=∠?④ 他是小张吗?⑤两直线相交只有一个交点。其中是命题的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
10、 下列说法正确的是( )
A. 只要有两边对应相等,再有一角对应相等,则这两个三角形全等
B. 如图,∠1=∠2,则m∥n的理由是“两直线平行,内错角相等”
C. 如图,若AB=CD,BC=DA,那么∠B=∠D
D. 已知三条线段的长,能画出一个三角形
11、 如图,已知AD∥BC,AE平分∠DAB,BE平分∠ABC,则∠E( )
A. 大于90° B. 等于90° C. 小于90° D. 无法确定
12、 下列命题中,是假命题的是( )
A. 全等三角形对应边上的高线相等 B. 绝对值等于本身的数是正数
C. 同位角相等,两直线平行 D. 若a=0,则ab=0
13、如图,AB∥CD,∠1=100°,∠2=130°,则∠3的度数为( )
A.50° B. 65° C. 40° D. 45°
14、如图,ΔABC中,∠A=50°,BO、CO分别是∠ABC、∠ACB的平分线,则∠BOC的度数是( )
A. 115° B. 110° C. 105° D. 130°
三、将下列命题改写成“如果……,那么……”的形式。
1. 平行于同一条直线的两直线平行。
改:
2. 互为相反数的两数它们的绝对值相等。
改:
3. 两条互相垂直的直线夹角为直角。
改:
四、尺规作图:(不写作法,保留作图痕迹)
1、 如图,已知∠MON,求作射线OP,使∠MOP=∠NOP
2、已知:线段a,b求作:⊿ABC,使AB=AC,BC=a ,高AD=b
3、已知:线段a和∠,求作:△ABC,使BC=a,∠BCA=∠。
4、求作ΔABC外接圆。
A
B C
5、已知:∠和线段,(如图4),求作:以∠为底角,为底边的等腰△ABC。
五、如图,已知∠1=∠2,AD=AB,求证:ΔABC≌ΔADC。
六、如图,若AD∥BC,AB∥CD,,,求的度数。
七、如图,已知AC⊥BD于C,CF=CD,BF的延长线交AD于点E,且AC=BC。求证:(1);(2)BE⊥AD。
八、如图,已知,求证:。
九、已知,如图DE // BF,BE // DF,AD // BC,AB // DC,求证:(1),(2)
十、如图2,ABCD是正方形,点E在BC上,DF⊥AE于F,请你在AE上确定一点G,使△ABG≌△DAF,并给予证明。
十一、已知:如图7,CE⊥AB与E,BD⊥AC于D,BD、CE、AO交于点O,且AO平分∠BAC
求证:OB=OC
十二、如图,BE⊥AE,CF⊥AE,垂足分别是E、F,D是EF的中点,△BED与△CFD全等吗?为什么?
十三、已知△ABC中,∠C = 90°,沿过B的一条直线BE折叠这个三角形,使点C与AB边上的一点D重合。如图所示。要使D恰为AB的中点,还应添加一个什么条件?(请你写出三种不同的添加条件)选择(1)中的某一个添加条件作为题目的补充条件,试说明其能使D为AB中点的理由。
解:(1)添加条件:①_____________;
②_______________;③________。
(2)说明:
十四、如图.AB=CD, ∠D=∠ECA, EC=FD,求证:AE=BF
十五、(6分)如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF交CD于点G,∠1=50,求∠2的度数。
十六、如图6.下面四个条件中,请你以其中两个为已知条件,第三个为结论,推出一个正确的命题(只需写出一种情况).①AE = AD ②AB = AC ③OB = OC ④∠B=∠C
十七、等腰梯形一底的中点对边的两个端点的距离会相等吗?若相等,请给出证明。若不相等,请说明理由。
十八、探究题
如图5,直线AB∥ED,求证:∠ABC+∠CDE=∠BCD。
图5
根据图中给出的作辅助线的3种方法,选择其中一种,写出证明过程。
教学目标:
1、通过问题的解决,图形的实例,体验全等图形的形成,体会到如何直观地判别两个图形是全等图形,通过动手实验进一步掌握全等图形的概念,全等多边形的特征;
2、了解全等多边形、对应边、对应顶点、对应角的概念;
3、培养学生动手试验的能力与习惯,树立实践出真知的观念。
重点难点:
难点:全等多边形的概念和特征;
重点:全等多边形的对应元素的确定。
教学准备:
动员学生课堂上带剪刀、厚纸板。教师带照片几张。
教学过程:
一、复习引入
1、问题1、请同学们观察老师手上的两张照片(1寸和2寸的照片),用你们学过的知识来回答观察到什么?
(两张照片是相似图形,其相似比是)
2、请几位同学说说相似图形的特征与识别。
3、问题2:请同学们再观察老师手上的两张照片(都是两寸的照片),也用数学的知识说说观察到什么?
(两个图形的形状、大小也一样,即相似比的相似图形)
本节开始,我们就来探索、研究这种图----§24.1图形的全等
二、新授
1、全等图形
试一试:(课本P78)你能找到几对形状相同、大小一样的图形吗?
(两对:(2)和(4)、(3)和(6))
问:如何判断两个图形的大小和形状是否完全相同的?
(学生各抒已见,给予表扬鼓励;通过师生之间交流,得出全等图形的形状和
大小都相等)
问:发挥你们的想像,两个大小和形状完全相同的图形叠合在一起,是否完全重合。动手试试。
(可用你们带来的工具)
(完全重合)
问:通过动手试验,你得到了什么结论?
(判断两个图形的大小和形状是否完全相同,可以把两个图形叠合在一起,看是否完全重合。)
我们把能够完全重合的两个图形叫做全等形。
练习:(1)课本试一试的图中的 就是全等形。
(2)课本 P80 练习
2、全等多边形及对应顶点、对应边、对应角的概念。
问题3:观察老师的演示(用大小一样的照片,演示翻折、旋转、平移的运动),请问:老师把这些图形进行哪些运动?形状、大小发生了改变吗?从中你得到了什么结论?
学生发表看法。
老师总结:我们把图形的翻折、旋转、平移称是图形的三种基本的运动,图形经过这样的运动,位置虽然发生了变化,但形状、大小却没有改变,前后两个图形是全等的。反过来,两个全等的图形经过这样的运动一定能够重合。
完成课本P79 思考。
由学生的回答中引出:
全等多边形:能够完全重合的两个多边形。
对应顶点:两个全等的多边形,经过运动而重合,相互重合的顶点。
对应边:相互重合的边。
对应角:相互重合的角。
如图24.1.3中的两个五边形是全等的,记作五边形ABCDE≌五边形A′B′C′D′E′.(这里,符号“≌”表示全等,读作“全等于”)(请同学们试指出两个图形的对应顶点、对应边和对应角。
练习:指出下列各图中的全等三角形,指出对应顶点、对应边、对应角。
由学生的练习中,引导学生讨论:如何记作全等形,能很快地指出对应边、对应角。可以小组讨论交流找出你认为较为科学、合理的方法。
(对应位置的字母,表示两个图形的对应顶点,比如△ABC≌△,A与,B与,C与是
对应顶点,对应顶点决定的边是全等三角形的对应边。)
练习:已知;四边形ABCDE≌四边形EFGH,写出它们所有的对应边及对应角。
3、全等多边形的特征、识别。
问题4:依据上面的分析,全等多边形有哪些特征呢?
全等多边形的对应边、对应角分别相等。
如五边形ABCDE≌五边形A′B′C′D′E′
对应角相等:, ,,
对应边相等:,,,
,
实际上这也是我们识别全等多边形的方法,即__________________________________的两个多边形全等。
例:如图(1)△ABC≌△DEF,你得到 ;
(2) ,可以得到△ABC≌△DEF。
练习:已知如图24.1.4△ABC≌△DEF,△ABC的周长是,,,求△DEF中,边DF的长度。
三、小结
对过本节学习,谈谈你的体会,收获,疑惑。
四、作业
P80习题24.1 1、2
24.2.1全等三角形的识别(1)
教学目标:
1、经历探索三角形全等条件的过程,体会如何探索研究问题。培养学生合作的精神,让学生体验分类的思想;
2、使学生懂得如何提出问题,分类讨论,并为以后研究提出问题。
重点难点:
1、难点:培养学生探索问题能力;
2、重点:掌握探索问题的方法。
教学过程:
一、复习
1、请一位同学叙述上一节所学的知识。
2、如图,△ABC≌△AEC,,,求出△AEC各内角的度数。
3、你是如何来识别两个三角形全等的?
从学生的回答中,提出:我们能不能找到一些较为简便的方法用来识别三角形的全等呢?有没有类似于相似三角形的识别方法呢?
回想一下,相似三角形有哪些识别方法?
本节开始,我们就一起来研究,探讨§24.2全等三角形的识别。
二、新授
要画一个三角形与老师在黑板上画的三角形ABC全等,需要几个与边或角的大小有关的条件呢?一个条件、两个条件、三个条件……
1、做一做
(1)只给一个条件:一条边,大家画出三角形,小组交流画的三角形全等吗?一个角,大家画出三角形,小组交流画的三角形全等吗?
(2)给出两个条件画三角形时,有几种可能的情况?这两个三角形一定会全等吗?分别按照下面条件,用刻度尺或量角器画三角形,并和周围的同学比较一下,所画的图形是否全等。
①三角形的一个内角为60°,一条边为3 cm;
② 三角形的两个内角分别为30°和70°;
③ 三角形的两条边分别为3 cm和5 cm
你们在画图和同学比较过程中,你能得出什么结论?
学生各抒己见后,教师归纳:你们一定会发现,如果只知道两个三角形有一个或两个对应相等的部分(边或角),那么这两个三角形不一定全等(甚至形状都不相同)。
2、议一议
如果给出三个条件画三角形,你能说出有哪几种可能的情况?
(有四种可能:三条边、三个角、两边一角和两角一边)
对于按以上每一种可能画得三角形是否全等,以后我们一起分别逐个探讨研究,现在我们先一起来完成以下几个练习。
三、巩固练习
1、如图,点O是平行四边形ABCD的对角线的交点,△AOB绕O旋转180 ,可以与△___________重合,这说明△AOB≌△___________.这两个三角形的对应边是AO与__________,OB与__________,BA与__________;对应角是∠AOB与________,∠OBA与_________,∠BAO与___________。
2、如图,△ABC是等腰三角形,AD是底边上的高,△ABD和△ACD全等吗?试根据等腰三角形的有关知
识说明理由
四、小结
让学生谈收获、体会、疑惑后,教师总结:本节通过画图实践可得,对于两个三角形的三条对应边、三个对应角中,只有满足其中一个条件或两个条件相等,两个三角形不一定全等。至于满足其中的三个条件相等的情况如何呢?请听下回分解。
五、作业
1、如图,△AOD≌△BOC,写出其中相等的角。
2、如图,△ABC≌△,,,
3、如图,△ABC≌△DEF,且A和D,B和E是对应顶点,则相等的边有 ,相等的角有 。
4、已知△ADC≌△CBA,且,写出相等的边、角。
5、如图,△ACD≌△ECB,A、C、B在一条直线上,且A和E是一对对应顶点,如果,那么将△ACD围绕C点顺时针旋转多少度与△ECB重合。
24.2.2全等三角形的识别(2)
教学目标:
1、使学生理解边边边公理的内容,能运用边边边公理证明三角形全等,为证明线段相等或角相等创造条件;
2、继续培养学生画图、实验,发现新知识的能力。
重点难点:
难点:让学生掌握边边边公理的内容和运用公理的自觉性;
重点:灵活运用SSS识别两个三角形是否全等。
教学过程:
一、创设问题情境,引入新课
请问同学,老师在黑板上画得两个三角形,△ABC与△全等吗?你是如何识别的。
(同学们各抒己见,如:动手用纸摹下一个三角形,剪下叠到另一个三角形上,是否完全重合;测量两个三角形的所有边与角,观察是否有三条边对应相等,三个角对应相等。)
上一节课我们已经探讨了两个三角形只满足一个或两个边、角对应相等条件时,两个三角形不一定全等。满足三个条件时,两个三角形是否全等呢?现在,我们就一起来探讨研究。
二、实践探索,总结规律
1、问题1:如果两个三角形的三条边分别相等,那么这两个三角形会全等吗?
做一做:给你三条线段、、,分别为、、,你能画出这个三角形吗?
先请几位同学说说画图思路后,教师指导,同学们动手画,教师演示并叙述书写出步骤。
步骤:
(1)画一线段AB使它的长度等于c(4.8cm).
(2)以点A为圆心,以线段b(3cm)的长为半径画圆弧;以点B为圆心,以线段a(4cm)的长为半径画圆弧;两弧交于点C.
(3)连结AC、BC.
△ABC即为所求
把你画的三角形与其他同学的图形叠合在一起,你们会发现什么?
换三条线段,再试试看,是否有同样的结论
请你结合画图、对比,说说你发现了什么?
同学们各抒己见,教师总结:给定三条线段,如果它们能组成三角形,那么所画的三角形都是全等的。
这样我们就得到识别三角形全等的一种简便的方法: 如果两个三角形的三条边分别对应相等,那么这两个三角形全等.简写为“边边边”,或简记为(S.S.S.)。
2、问题2:你能用相似三角形的识别法解释这个(SSS)三角形全等的识别法吗?
(我们已经知道,三条边对应成比例的两个三角形相似,而相似比为1时,三条边就分别对应相等了,这两个三角形不但形状相同,而且大小都一样,即为全等三角形。)
3、问题3、你用这个“SSS”三角形全等的识别法解释三角形具有稳定性吗?
(只要三角形三边的长度确定了,这个三角形的形状和大小就完全确定了)
4、范例:
例1 如图24.2.2,四边形ABCD中,AD=BC,AB=DC,
试说明△ABC≌△CDA.
解:已知 AD=BC,AB=DC,
又因为AC是公共边,由(S.S.S.)
全等识别法,可知△ABC≌△CDA
5、练习:
P84 练习1、2
6、试一试:已知一个三角形的三个内角分别为、、,你能画出这个三角形吗?把你画的三角形与同伴画的进行比较,你发现了什么?
(所画出的三角形都是相似的,但大小不一定相同)。
三个对应角相等的两个三角形不一定全等。
三、加强练习,巩固知识
1、如图,,,△ABC≌△DCB全等吗?为什么?
2、如图,AD是△ABC的中线,。与相等吗?请说明理由。
四、小结
本节课探讨出可用(SSS)来识别两个三角形全等,并能灵活运用(SSS)来识别三角形全等。三个角对应相等的两个三角不一定会全等。
五、作业
P90习题24.2 1
24.2.3全等三角形的识别(3)
教学目标:
1、使学生掌握SAS的内容,会运用SAS来识别两个三角形全等;
2、通过识别全等三角形的识别的学习,使学生初步认识事物之间的因果关系与相互制约关系,学习分析事物本质的方法;
3、经历如何总结出全等三角形识别方法,体会如何探讨、实践、总结,培养学生的合作能力。
重点难点:
1、难点:三角形全等的识别:SAS;
2、重点:对全等三角形的识别的理解和运用。
教学过程:
一、复习
1、什么叫全等图形?什么叫做全等三角形?
(能够完全重合的两个图形叫做全等形,能够完全重合的两个三角形叫做全等三角形)。
2、将全等的△ABC与△DEF重合,再沿BC方向将△DEF推移如图位置,问线段AD与BE数量关系怎样?BC与EF位置关系怎样?为什么?
解: ,BC∥EF
∵ △ABC≌△DEF
∴
∴
∴
又∵ △ABC≌△DEF
∴
∴ BC∥EF ]
(虽然本教材没有采用∵∴的形式,但根据《课标》的精神,结合其他版本教材,如北师大的版本,建议可以采用,可以使解题简捷。)
3、已知:如图,,,,,求的大小。
解:,,
∴ △ACB≌△AED
∴
∴
∴
∴]
二、新授
1、引入;上一节课,我们已经知道两个三角形满足三个条件的三条边对应相等和三个角对应相等的情况。情况如何呢?
(三条边对应相等两个三角形;三个角对应相等的两个三角形不一定全等)
如果两个三角形有两条边和一个角分别对应相等,这两个三角形会全等吗?-------这就是本节课我们要探讨的课题。
2、问题1:如果已知一个三角形的两边及一角,那么有几种可能的情况呢?
(应该有两种情况:一种是角夹在两条边的中间,形成两边夹一角;另一情况是角不夹在两边的中间,形成两边一对角。)
每一种情况下得到的三角形都全等吗?
3、做一做
(1)如果“两边及一角”条件中的角是两边的夹角,比如三角形两条边分别为和,它们的夹角为,你能画出这个三角形吗?你画的与同伴画的一定全等吗?
换两条线段和一个角试试,你发现了什么?
同学们各抒己见后总结:发现对于已知的两条线段和一个角,以该角为夹角,所画的三角形都是全等的。
这就是判别三角形全等的另外一种简便的方法:
如果两个三角形有两边及其夹角分别对应相等,那么这两个三角形全等.简写成“边角边”或简记为(S.A.S.)
你能用相似三角形的识别法来解释这种“SAS”识别三角形全等的方法吗?
(一个角对应相等而夹这个角的两边对应成比例的两个三角形相似,当相似比为1时,夹这个角的两
边对应相等,这两个三角形的形状、大小都相同,即为全等三角形)
(2)如果“两边及一角”条件中的角是其中一边的对角,比如两条边分别为和,长度为的边所对的角为,情况会怎样呢
请画出这个三角形,把你画的三角形与其他同学画的三角形进行比较,由此你发现了什么?
(两边及其中一边的对角对应相等,两个三角形不一定全等。)
4、范例:如图,△ABC中,AB=AC,AD平分∠BAC,试说明△ABD≌△ACD.
解 已知 AB=AC,∠BAD=∠CAD,
又AD为公共边,由(S.A.S.)全等识别法,可知
△ABD≌△ACD
三、巩固练习
P86 练习1、2
四、小结
学生谈收获、体会、疑惑后,进一步总结本节学习了三角形全等的识别的另一种SAS,而两边及其中一边的对角对应相等的两个三角形不一定全等,注意观察图形的特征,找出是否具备满足两个三角形全等的条件。
五、作业
P90 习题24.2 2
24.2.4全等三角形的识别(4)
教学目标:
1、使学生理解ASA的内容,能运用ASA全等识别法来识别三角形全等进而说明线段或角相等;
2、通过画图、实验、发现、应用的过程教学,树立学生知识源于实践用于实践的观念。使学生体会探索发现问题的过程。经历自己探索出AAS的三角形全等识别及其应用。
重点难点:
难点:三角形全等的识别法ASA和AAS及应用;
重点:利用三角形全等的识别法,间接说明角相等或线段相等。
重点难点:
剪刀、卡纸。
教学过程:
一、复习
1、什么叫做全等三角形,如何识别两个三角形全等?
(能够完全重合的两个三角形叫做全等三角形。识别两个三角形全等的方法有:SSS;SAS)。
2、叙述SSS、SAS的内容。
3、已知:如图,,,请问再加上什么条件下,△ABC≌△,并说明理由。
(,根据SSS;,根据SAS)。
二、新授
1、引入:请问到本节为止,我们探讨两个三角形满足三个条件的哪几种情况,情况如何呢?
(如果两个三角形有三条边分别对应相等或两个三角形有两条边及其夹角分别对应相等,那么这两个三角形就一定全等。如果两个三角形有三个角分别对应相等,或两个三角形的两边及其一边所对的角对应相等,那么这两个三角形不一定全等。)
还有哪些情况还没有探讨呢?
(如果两个三角形的两个角及一条边分别对应相等,这两个三角形一定全等吗?)
本节我们闵来探讨两个三角形的两个角及一条边分别对应相等,这两个三角形是否全等的课题。
2、问题1:如果把已知一个三角形的两角及一边,那么有几种可能的情况呢?
(一种情况是两个角及两角的夹边;另一种情况是两个角及其中一角的对边。)
每一种情况下得到的三角形都全等吗?
3、请同学们动手做一个实验:同桌两位同学为一组。
(1)共同商定画出任意一条线段AB,与两个角、()
(2)两位同学各自在硬纸板上画线段的长等于商定的线段AB的长,在的同旁,画等于商定的,画等于商定的,设与相交于,便得△。
(3)用剪刀各自剪出△,将同桌同学剪出的两个三角形重叠在一起发现了什么?其他各桌的同学是否也有同样的结论呢?
同学们各抒己见后,总结:对于已知两个角和一条线段,以该线段为夹边,所画的三角形都是全等的.
由此得到另一个识别全等三角形的简便方法:
如果两个三角形的两个角及其夹边分别对应相等,那么这两个三角形全等.简记为“角边角”或简记为(A.S.A.)。
4、问题2:试说明ASA全等识别法与相似三角形的识别法有什么类似的。
(两个角对应相等的两个三角形相似,当这两个角的公共边相等时,这两个三角形的形状、大小都相同,即为全等三角形。)
5、思考:如图,如果两个三角形有两个角及其中一个角的对边分别对应相等,
那么这两个三角形是否一定全等?
动手画一画:比如,,,你能画这个三角形吗?
提示:这里的条件与实验中的条件有什么相同点与不同点?你能将它转化为实验中的条件吗?
你画的三角形与同伴画的一定全等吗?
现在两组同学按如果角所对的边为画,另两组同学换两个角和一条线段,试试看,你们得出什么结论?
同学们各抒己见后,总结:对于已知两个角和一条线段,以该线段为夹边,所画的三角形都是全等的.
由此得到另一个识别全等三角形的简便方法:
如果两个三角形的两个角及其夹边分别对应相等,那么这两个三角形全等.简写成:“角角边”或简记为(A.S.A.)。
6、问题3:你能说说ASA与AAS这两种全等识别法间的关系吗?
(AAS识别法可由ASA识别法推导出来,如上图中,因为,,由于,,所以,于是△ABC与△DEF具备ASA全等。)
7、范例
如图,,,试说明△ABC≌△DCB
解:已知,
又BC是公共边,由(ASA)全等识别法,
可知△ABC≌△DCB
三、巩固练习
P88练习 1、2
四、小结
用采访的形式访问一些同学,本节学到什么知识,对这些知识有什么体会,对本节的知识存在着哪些疑问。
五、作业
P90习题24.2 3、4、5
24.2.5全等三角形的识别(5)
教学目标:
1、帮助学生总结一般三角形全等的识别条件,使他们自觉运用各种全等识别法进行说理;
2、通过一般三角形全等识别条件的归纳,帮助学生认识事物间存在着的因果关系和制约的关系。
重点难点:
重点:让学生识别三角的哪些元素能用来确定三角形的形状与大小,因而可用来识别三角形全等。
难点:灵活应用各种识别法识别全等三角形。
教学准备:
卡纸剪出的图1、2中的六个三角形。
I II I III
III II
(图1) (图2)
教学过程:
一、复习
1、识别两个三角形全等的条件有哪些?
(有SAS、ASA、AAS、SSS四种)
2、一个三角形共有三条边与三个角,你是否想到这样一问题了:除了上述四种识别法,还有其他的三角形全等识别法吗?比如说“SSA”、“AAA”能成为判定两个三角形全等的条件吗?
二、新授
1、演示
(1)演示图1中的I、II三角形,它们间有两边及一对角对应相等,这两个三角形能完全重合,是全等形。但再取出III的三角形与I叠在一起后,发现它们不重合不是全等形,因此我们进一点证实了:有两边和其中一边的对角对应相等的两个三角形不一定全等。“SSA”不是识别三角形全等的方法。
(2)演示图2中的I、II三角形,它们间有三个角对应相等,这两个三角形能完全重合,是全等形,但再取出III的三角形与I叠在一起后,发现它们不重合,不是全等形。因此我们进一步证实了:三个角对应相等的两个三角形不一定全等“AAA”也不是识别三角形全等的方法。
2、填下表(挂出小黑板,让学生思考、讨论,共同填答)。
两个三角形中对应相等的元素 两个三角形是否全等 依据的识别法 反例
SSS √ SSS
SAS √ SAS
SSA X 可举反例
ASA √ ASA
AAS √ AAS
AAA X 可举反例
3、范例
例:如图,,,点F是CD的中点,吗?试说明理由。
教学要点:
(1)分析题目结论假定,可转化为,需证它们所在的两个三角形全等;
(2)观察图形,、中,并不在三角形中,为此添辅助线AC、AD;
(3)在△ACF与△ADF中,已知AF是公共边,CF=FD,尚缺一条件,它只能是AC与AD相等;
(4)为证AC与AD相等。又要找它们分别在的△ACB与△ADE;
(5)△ACB与△ADE,由已知条件可由SAS证它们全等;
(6)书写范例。
解:连结AC、AD,由已知AB=AE,,BC=DE
由SAS三角形全等识别法可知:
△ABC≌△AED
根据全等三角形的对应相等可知
由,,(公共边),
根据SSS可知△ACF≌△ADF
根据全等三角形的对应角相等可知
又由于F在直线CD上,可得,即。
你们可有其他方法吗?
三、巩固练习
1、如图,在△ABC中,,,试说明△AED是等腰三角形。
2、如图,AB∥CD,AD∥BC,与,与相等吗?说明理由。
四、小结
由学生对本节的学习过程进行总结。
五、作业
(一)、填空题:
1、有一边对应相等的两个 三角形全等;
2、有一边和 对应相等的两个三角形全等;
3、有两边和 一角对应相等的两个三角形全等;
4、如图,AB∥CD,AD∥BC,AC、BD相交于点O。
(1)由AD∥BC,可得 = ,由AB∥CD,可得 = ,又由 ,于是△ABD≌△CDB;
(2)由 ,可得AD=CB,由 ,可得△AOD≌△COB;
(3)图中全等三角形共有 对。
(二)、选择题:
1、若△ABC≌△BAD,A和B、C和D是对应顶点,如果,,,则BC的长是( )
A、 B、 C、 D、无法确定
2、下列各说法中,正确的是( )
A、有两边和一角对应相等的两个三角形全等;
B、有两个角对应相等且周长相等的两个三角形全等;
C、两个锐角对应相等的两个直角三角形全等;
D、有两组边相等且周长相等的两个三角形全等。
(三)、解答题:
1、如图,,,AC、BD交于点
,图中共有几对长度相等的线段,
你是通过什么办法找到的?
2、如图,,,
(1)等于多少度?
(2)图中有哪几组平行线?
(3)与的和是定值吗?
24.2.6全等三角形的识别(6)
教学目标:
1、经历探索直角三角形全等条件的过程,掌握直角三角形全等的条件,并能运用其解决一些实际问题;
2、学习事物的特殊、一般关系、发展逻辑思维能力。
重点难点:
重点:让学生掌握直角三角形全等的“HL”识别法;
难点:理解直角三角形为内角在构造三角形时特殊性,并能灵活地运用各种全等识别法识别两个直角三角形全等是否全等。
教学准备:
剪刀、卡纸。
教学过程:
一、复习
如图,△ABC和△都是直角三角形,请你用所学的知识,须加上什么条件直角△ABC和△全等。并说明理由。
[,,(SAS);
,(ASA);
,,,(SSS)
,(AAS)]
等,让学生抢答。
二、创设问题情境
问题:舞台背景的形状是两个直角三角形。工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆计划遮住无法测量。
1、你能帮他想个办法吗?
2、如果他只带了一个卷尺,能完成这个任务吗?
[问题1,学生可以回答去量斜边和一锐角,或直角边和一个锐角;但对于问题2,学生则难肯定]。
工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”,你相信他的结论吗?
三、动手实践,探索新知
试以两条线段,,分别为直角边和斜边在卡纸上画一个三角形。
按照下面的步骤做一做:
(1)作;
(2)在射线CM上截取线段;
(3)以A为圆心,以长为半径画弧,交射线CN于点B;
(4)连结AB。
问: (1)△ABC就是所求作的三角形吗?(是的)
(2)剪下这个三角形,和其他同学所作的三角形进行比较,它们能重合吗?你发现了什么?
(能重合;发现:两个直角三角形的斜边及一条直角边分别对应相等,那么这两个直角三角形全等)
(3)你能用所学的知识来解决你的发现吗?
(由勾股定理可知,另一条直角边也是对应相等的)
因此可以得到如下结论:
如果两个直角三角形的斜边及一条直角边分别对应相等,那么这两个直角三角形全等. 简记为(H.L.)
四、想一想
你可以用几种方法说明两个直角三角形全等?
五、例题
如图24.2.13,AB是圆O的直径,AC=AD,试说明△ABC和△ABD全等.
解:因为AB为⊙O的直径,所以
∠ACB=∠ADB=90°.
又 AC=AD,AB=AB,
由(H.L.)全等识别法,可知
△ABC≌△ABD
六、巩固练习
P89 练习1、2
七、小结
学生谈谈收获、疑惑。总结本节学习直角三角形全等的识别,除了一般三角形全等识别法外,还有“HL”。
八、作业
P90 习题24.2 6
24.3.1定义、命题与定理
教学目标:
1、了解定义、命题、真命题、假命题、定理的含义,会区分命题的条件(题设)和结论,奠定推理论证的基础;
2、初步体会合理化思想,使学生明确什么定理及其意义。
重点难点:
1、重点:定义、命题、公理、定理的概念;
2、难点:判定什么定义、命题、定理、公理,及找出命题的题设和结论。
教学过程:
一、创设问题情境引入
情境1:小亮和小刚正在津津有味地阅读《我们爱科学》。
小亮:“哈!这个黑客终于被逮住了。”
小刚:“是的,现在英特网广泛运用于我们的生活中,给我带来了方便,但……”
坐在旁边的两个人一边听着他的谈话,一边也在悄悄议论着。
“这个黑客是个小偷吗?”
“可能是喜欢穿黑衣服的贼。”
“那因特网肯定是一张很大的网。”
“估计可能是英国造的特殊的网。”
你听完这则片段故事,有何想法?
同学们各抒己见后,老师给予同学的各种回答评价后,发表自己的看法:在日常生活中,我们会遇到许多概念,假如不对这些概念下定义,别人就无法理解这引起概念,以致无法进行正常的交流。同样,在数学学习中,要进行严格的论证,也必须首先对所涉及的概念下定义。本节我们就一起来学习——§24.3命题与证明的第一节定义、命题与定理。
练习:课本P93 练习1
二、共同探索获得新知
1、试一试:得出定义
你是如何找出图中的平行四边形呢?
“有两组对边分别平行的四边形叫做平行四边形”这句话说明了平行四边形的含义以及区别于其他图形的特征。
一般地,能明确指出概念含义或特征的句子,称为定义。
例如:(1) 有一个角是直角的三角形,叫做直角三角形.
(2) 有六条边的多边形,叫做六边形.
(3) 在同一平面内,两条不相交的直线叫做平行线.
你还能举出一些其他的例子吗?
观察这些定义,你发现定义中用词有什么特征?
同学们各抒己见后,总结:定义必须是严密的.一般避免使用含糊不清的术语,比如“一些”、“大概”、
“差不多”等不能在定义中出现.正确的定义能把被定义的事物或名词与其他的事物或名词区别开来。
2、思考:得出命题
思考:试判断下列句子是否正确。
(1)如果两个角是对顶角,那么这两个角相等;
(2)三角形的内角和是180°;
(3)同位角相等;
(4)平行四边形的对角线相等;
(5)菱形的对角线相互垂直
根据已有的知识可以判断出句子(1)、(2)、(5)是正确的,句子(3)、(4)是错误的.像这样可以
判断它是正确的或是错误的句子叫做命题(proposition).正确的命题称为真命题,错误的命题称为假命题。
练习:
(1)下列句子哪些是命题?
①动物都需要水;
②猴子是动物的一种;
③玫瑰花是动物;
④美丽的天空;
⑤对应角都相等的两个三角形一定全等;
⑥负数都小于零;
⑦你的作业做完了吗?
⑧所有的质数都是奇数;
⑨过直线外一点作l的平行线;
⑩如果,,那么。
(2)练习:课本P93 练习3
3、观察发现,命题结构。
观察下列命题,你能发现这些命题有什么共同的结构特征?与同样交流。
(1)如果两个三角形的三条边相等,那么这两个三角形全等;
(2)如果一个三角形是等腰三角形,那么这个三角形的两个底角相等;
(3)如果一个四边形的对角线相等,那么这个四边形是矩形;
(4)如果一个四边形的一组对边平行且相等,那么这个四边形是平行四边形;
(5)如果一个四边形的两条对角线互相垂直,那么这个四边形是菱形。
总结:在数学中,许多命题是由题设(或条件)和结论两部分组成的.题设是已知事项,结论是由已知事项推出的事项.这种命题常可写成“如果……那么……”的形式.其中,用“如果”开始的部分是题设,用“那么”开始的部分是结论.例如,在命题(1)中,“两个角是对顶角”是题设,“这两个角相等”是结论。
例、把命题“在一个三角形中,等角对等边”改写成“如果……那么……”的形式,并分别指出命题的题设与结论.
解:这个命题可以写成:“如果在一个三角形中有两个角相等,那么这两个角所对的边也相等.” 这里的题设是“在一个三角形中有两个角相等”,结论是“这两个角所对的边也相等”。
练习:课本P93 练习2
4、追溯根源:明确定理
问题:如何证实一个命题是真命题呢?
用我们以前学过的观察、实践、验证特例等方法。这些方法往往并不可靠。
能不能根据已经知道的真的命题证实呢?那已知知道的真命题又是如何证实呢?
哦……那可怎么办?
其实,在数学发展史上,数学家们也遇到类似的问题。公元前3世纪,人们已经积累了大量的数学知识,在此基础上,古希腊数学家欧几里得编写了一本书,书名叫《原本》。为了说明每一个结论的正确性,他在编写这本书时进行了大胆创造:挑战了一部分数学名词和一部分公认的真命题作为证实其他命题的起始依据,其中数学名词称为原名,公认的真命题称为公理。即数学中有些命题的正确性是人们在长期实践中总结出来的,并把它们作为判断其他命题真假的原始依据,这样的真命题叫做公理。
小组竞赛:
请你说出学过知识中,哪些是公理,哪组说的又多又准就是获胜者。
如:
(1)一条直线截两条平行直线所得的同位角相等;
(2)两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行;
(3)如果两个三角形的两边及其夹角(或两角及其夹边,或三边)分别对应相等,那么这两个三角形全等;
(4)全等三角形的对应边、对应角分别相等
此外,我们把等式、不等式的有关性质以及等量代换(即在等式或不等式中,一个量用它的等量替代)都作为逻辑推理的依据.
有些命题可以从公理或其他真命题出发,用逻辑推理的方法判断它们是正确的,并且可以进一步作为判断其他命题真假的依据,这样的真命题叫做定理(theorem).
例如,运用公理“两角及其夹边分别对应相等的两个三角形全等”,可以得到定理:“两角及其一角的对边分别对应相等的两个三角形全等.”
男女对抗赛:由男女同学各说定理,并分别由对方判断正误,说对一个定理得1分,高分都获胜。
三、巩固知识、归纳总结
同学们,本节你学到了哪些知识?有何体会?还有什么疑惑呢?若同学有疑惑,还可一起讨论,帮助解惑。
四、作业
P93 习题24.3 1、2
24.3.2证明(1)
教学目标:
1、初步了解证明意义及基本步骤和书写格式;
2、感受几何中推理的严谨、结论的确定;
3、体验举反例说明命题是假命题。
重点难点:
1、重点:证明的基本步骤和书写格式;
2、难点:几何中的逻辑推理。
教学过程:
一、复习
问题1:一位同学在钻研数学题时发现:
2+1=3,
2×3+1=7,
2×3×5+1=31,
2×3×5×7+1=211
于是,他根据上面的结果并利用素数表得出结论: 从素数2开始,排在前面的任意多个素数的乘积加1一定也是素数.他的结论正确吗?
计算一下,你发现什么?
问题2:如图所示,一个同学在画图时发现: 三角形三条边的垂直平分线的交点都在三角形的内部。于是他得出结论: 任何一个三角形三条边的垂直平分线的交点都在三角形的内部.他的结论正确吗?
画一个钝角三角形试试看。
问题3:我们曾经通过计算四边形、五边形、六边形、七边形、八边形等的内角和,得到一个结论: n边形的内角和等于(n-2)×180°.这个结果可靠吗?是否有一个多边形的内角和不满足这一规律?
问题4:以上3个问题的解决中,你有何体会呢?
上面几个例子说明: 通过特殊的事例得到的结论可能正确,也可能不正确.因此,通过这种方式得到的结论,还需进一步加以证实。
本节就来学习解决此问题的知识-------证明。
二、新授
1、证明的概念
根据题设、定义以及公理、定理等,经过逻辑推理,来判断一个命题是否正确,这样的推理过程叫做证明。
2、证明一个命题是真命题
(1)前面的学习已经告诉我们:一条直线截两条平行线所得的内错角相等.下面我们运用前面所提到的基本事实,即公理来证明这个结论.
例1 证明: 一条直线截两条平行直线所得的内错角相等.
已知: 如图24.3.3,直线l1∥l2,直线l3分别和l1、l2相交于点A、B.
求证: ∠1=∠3.
证明: 因为 l1∥l2(已知),
所以 ∠1=∠2 (两直线平行,同位角相等).
又 ∠2=∠3 (对顶角相等),
所以 ∠1=∠3 (等量代换)
(2)总结
观察老师的范例你有何体会?
同学们各抒已见后,总结证明一下命题是真命题的步骤:
①根据命题画出图形,标上字母;
②结合图形写出已知、求证;
③有题设、定义以及公理、定理等,经过逻辑推理,得出正确的结论。
(3)练习
①课本P96 练习1;
②证明:同旁内角互补,两直线平行。
证明一个命题是假命题
如果要证明或判断一个命题是假命题,怎么办呢?
(1)范例
例,证明“一个锐角与一个钝角的和等于一个平角”是假命题,只要举出一个符合命题题设而不符合结论的例子就可以了,这称为“举反例”。
解:例如锐角等于30°,钝角等于120°,但它们的和就不等于180°,从而说明这个命题是假命题。
(2)练习
①课本P96 练习2
②举反例说明“一个数的绝对值大于这个数的本身。”是个假命题。
三、小结
本节学习了什么是证明,以及如何证明一个命题是真命题及假命题。特别是证明一个命题是真命题时,要注意须画出图形,写出已知、求证,并用逻辑推理出正确的结论。
四、作业
P97 习题24.3 3
课题 :24.3.3证明(2)
教学目标:
1、进一步理解和总结证明的步骤、格式和方法;
2、让学生在动口、动手、动脑的实践,直接经验、自己活动中获取知识,培养了学生的发散思考。
重点难点:
重点:掌握证明的步骤、格式和方法;
难点:熟练地证明。
教学过程:
一、复习引入
1、什么是证明?
(根据题设、定义以及公理、定理等,经过逻辑推理,来判断一个命题是否正确,这样的推理过程叫做证明)
2、如何证明一个命题是假命题?
(证明或判断一个命题是假命题,那么我们只要举出一个符合命题题设而不符合结论的例子就可以了)
3、你是如何证明了一个命题是真命题呢?
同学们各抒己见,我们今天这一节课继续来对所表述的结论是正确的通过推理的方式给予证明。
二、新授
1、范例1
例:内错角相等,两直线平行.
已知:如图24.3.4,直线l3分别交l1、l2于点A、点B,∠1=∠2.
求证: l1∥l2.
证明 因为 ∠1=∠2 (已知)
∠1=∠3 (对顶角相等)
所以 ∠2=∠3 (等量代换)
所以 l1∥l2 (同位角相等,两直线平行)
与你上节完成课时作业设计中此题的过程进行对比,你有何感受?请你对证明步骤进行总结,并与同伴交流。
证明步骤的一种可供参考的说法是:
(1)理解题意;
(2)根据题意正确画出图形;
(3)根据题意写出“已知”和“求证”;
(4)分析题意,探索证明的思路;
(5)依据寻求的思路,运用数学符号和数学语言条理清晰地写出证明过程;
(6)检查表达过程是否正确、完善。
2、范例2
例:已知:如图24.3.5,AB和CD相交于点O,∠A=∠B.
求证: ∠C=∠D
证明: 因为 ∠A=∠B(已知)
所以 AC∥BD (内错角相等,两直线平行)
所以 ∠C=∠D (两直线平行,内错角相等)
三、试一试
请在下面题目证明中的括号内填入适当的理由.
已知:如图24.3.6,AD=BC,CE∥DF,CE=DF.
求证: ∠E=∠F.
证明: 因为 CE∥DF ( ),
所以 ∠1=∠2 ( ).
在△AFD和△BEC中,因为
DF=CE ( ),
∠1=∠2 ( ),
AD=BC ( ),
所以 △AFD≌△BEC ( ),
所以 ∠E=∠F ( ).
四、巩固练习
1、已知:如图,直线AB、CD被EF、GH所截,∠1=∠2,求证:∠3=∠4.
2、已知:如图,AB=AC, ∠BAO=∠CAO.求证:OB=OC
五、小结
学生谈谈收获、疑惑。
八、作业
P97 习题24.3 4、5、6
课题 :24.4.1 尺规作图(1)画线段
教学目标:
1、会用尺规作一条线段等于已知线段;
2、明白尺规作图的意义和历史,并激发学生的学习兴趣。
重点难点:
重点:用尺规作一条线段等于已知线段;
难点:灵活地运用“作一线段等于已知线段”进行作图。
教学过程:
一、追溯根源,激发兴趣
你可以很容易地用量角器和刻度尺画一条线段等于已知线段,画一个角等于已知角.但如果限定使用的工具只能是圆规和没有刻度的直尺,即尺规作图,你还能画出符合条件的图形吗?
为什么对几何图要作出只用尺规作用的限制?
自古希腊时代起,人们就已经创造了尺规作图的游戏,这是一个十分有趣的游戏,吸引着许多人去探索。希腊人认为,几何的基本原则是只用极少的定义、公理推导出尽可能多的命题,因此作图的工具也要限制到不能再少的程度。希腊人还认为,学几何是为了训练思维,靠人去思考,而不是靠作图工具。因此,就规定了作图只能使用直尺和圆规这两种最简单的工具。
希腊的平面几何学(也就是现在世界通行的平面几何学)的作图方法规定:直尺无刻度,它的用法是经过两点可以作一直线;可以无限制地延长一直线。圆规的用法是以任意给定的点为中心,以任意给定的长为半径,可以作圆或画弧。用圆规、直尺作图时只能有限次使用圆规和直尺。此外还规定对于直线与直线、直线与圆(或弧)、圆(或弧)与圆(或弧)相交可以求它们的交点,这一整套的规定也称为平面几何作图公法。
对直尺和圆规能作出哪些图形以及不可能作出哪些图形的思考,竟推动了不整个数学的发展。本节开始,我们就来一起学习-----§24.4 尺规作图。本节就从最基本的图形开始-----画线段。
1、 试一试
如图24.4.1,MN为已知线段,你能用直尺和圆规准确地画一条与MN相等的线段吗?
你是如何画图呢?与同伴进行交流,请一些同学展示其成果。
作法:
(1)如图24.4.2,画射线AB,
(2)在射线AB上截取AC=MN(即:用圆规量出线段MN的长,以点A为圆心,以MN的长为半径画弧,交射线AB于点C。)
所以,线段AC就是所要画的线段.
三、做一做
如图,已知线段和两条互相垂直的直线AB、CD。
(1)利用圆规,在射线OA、OB、OC、OD上作线段、、、,使它们分别与线段相等;
(2)依次连接、、、、。
你得到了一个怎样的图形?与同伴交流。
[作图时,要求学生能口头表述作法,并能正确作出图形(保留作图痕迹),作出图形应为正方形。]
四、练一练
1、如图,已知线段和,直线AB、CD垂直且相交于O。
利用尺规,按下列要求作图:
(1)在射线OA、OB、OC上作线段、、,使它们分别与线段相等;
(2)在射线OD上作线段,使等于;
(3)依次连接、、、、。
你得到了一个怎样的图形?与同伴交流。
2、已知线段、和,求作:线段,使;
3、课本P100 练习1
五、说一说
(1)本节你学到了什么?
(2)你是如何用尺规画一条线段的?
(3)通过本节的学习,你有何体会?
六、作业
P103 习题24.4 1
课题 :24.4.2 尺规作图(2)画角
教学目标:
1、使学生掌握一个角等于已知角的基本作图;;
2、初步训练学生用规范的语言叙述尺规作图的动作,达到作图准确,叙述正确;
3、灵活运用画一个角的尺规作图,画一些其他图形。
重点难点:
重点:掌握用尺规画一个角及灵活运用画一个角在画其他图形中的使用;
难点:画图的几何语言叙述。
教学过程:
一、创设问题情境,激发学生兴趣
问题:如图,要在长方形木板截一个平行四边形,使它的一组对边在长方形木板的边缘上,另一组对边中的一条边为AB。
1、请过C点画出与AB平行的另一条边;
2、如果你只有一个圆规和一把没有刻度的直尺能解决这个问题吗?
你想如何处理此问题?
分析:要在长方形木板上截一个平行四边形,按图的方式(平行四边形的一组对边在长方形的边缘上),只要保证过点C作出与AB平行的另一条线段即可。而要过点C作AB的平行线,可以通过作一个角等于即可。
本节我们就来一起学习用尺规作一个角等于已知角。
二、试一试
图24.4.3,∠AOB为已知角,按下列步骤用圆规和直尺准确地画一个角等于∠AOB.
1、画射线O′A′;
2、以点O为圆心,以适当长为半径画弧,交OA于C,交OB于D;
3、以点O′为圆心,以OC长为半径画弧,交O′A′于C′.;
4、以点C′为圆心,以CD长为半径画弧,交前一条弧于D′;
5、经过点D′画射线O′B′;
所以,∠A′O′B′就是所要画的角。
用量角器验证你作的角与已知角是否相等。
(相等)
你能用所学的知识说明其中的理由吗?
(因为在作图过程知道:,,,所以△COD≌△,根据全等三角形对应角相等,可知。)
三、练一练
1、利用尺规完成本节课开始提出的问题。
2、已知,利用尺规作,使
3、课本P100 练习2
四、做一做
请你利用直尺和圆规分别画出满足图24.4.4和图24.4.5中条件的三角形ABC.
1、已知两边及夹角;
(不写画法,保留作图痕迹)
学生讨论后,教师示范。边叙述画法边画,学生跟着画。
(1)作;
(2)在射线BM上截取;
(3)在射线BN上截取;
(4)连结AC。
所以,△ABC就是所画的三角形。
还有其他的画法吗?动手试一试。
(如,先线段,画,在射线BM上截取,连结AC,即得△ABC)。
你从画图得到了什么?
同学们各抒己见。
(观察一个图形是由几个点确定了,能否画出这些点,若能,就可画出这个图形,若不能,就无法画出这个图形,为了便于分析,可画出草图)。
2、已知两角及夹边.
画完后,同学相互交流,指出对方的不足,或向对方提出问题,并请同学上板演示。
五、说一说
1、你本节学到了什么?
2、在你所学的知识中重点是什么?
3、在你所学的知识中注意什么?
4、你在本节的学习过程有何想法?
六、作业
P103 习题24.4 2、3
课题 :24.4.3 尺规作图(3)画垂线
教学目标:
1、使学生掌握作线段的垂直平分线,过一点作已知直线垂线的两种基本作图;
2、继续训练学生用简练、准确地运用几何语言表达作图方法与步骤,认识它的正确性、合理性;
3、培养学生探索问题、解决问题的方法,经历如何画线段的垂直平分线,体验利用画线段垂直平分线的方法为基础,画过一点作已知垂线的作图。
重点难点:
重点:让学生掌握过一点作直线的垂线,作直线的垂直平分线的基本方法;
难点:理解作图的理论依据。
教学过程:
一、复习
1、什么叫做尺规作图?
(限定用直尺和圆规来画图,称为尺规作图)
2、用尺规作图
(1)作线段,使它等于已知线段的长;
(2)作角,使它等于已知角;
①让学生在练习本上画任意长的线段和任意角。
②提问学生口述作法,教师在黑板上操作尺规画图,或教师口述作图步骤,让学生按老师的口述,操作尺规作图。
作线段:已知线段,作射线AC,以A为圆心,在AC上截取,AB就是所求作的;
作角:已知,作射线,以O为圆心,以任意长为半径作弧,分别交OA、OB于D、C两点,以为圆心,以OC为半径作弧,交于,以点为圆心,以CD长为半径作弧,交前弧于,经过作射线,就是所求的角。
3、什么垂直平分线?
(过线段的中点,垂直这条线段的直线)
4、线段垂直平分线有哪些特征?
(线段的垂直平分线上的点到线段两端点的距离相等;反过来,到线段两端点距离相等的点在线段的垂直平分线上)
二、做一做
如图,如图24.4.6,已知线段AB,画出它的垂直平分线.
提示:由线段垂直平分线的特征能否为你提供一些作图的依据。
若有学生懂得画,请他上台展示;若讨论没有结果的话,教师示范。
作法:1、分别以A、B两点为圆心,以大于长为半径画弧,两弧相交于C、D两点;
2、过C、D两点作直线CD。
所以,直线CD就是所求作的。
三、议一议
能否说出这种画法的依据,小组讨论交流。并发表小组的共识。
我们知道,线段的垂直平分线上的点到线段两端点的距离相等;反过来,到线段两端点距离相等的点在线段的垂直平分线上,因此如果能找到两个到线段两点的距离相等的点,那么过这两点就可画线段的垂直平分线。
如图,以点A为圆心,以大于AB一半的长为半径,在AB的一侧画弧; 以点B为圆心,以同样的长为半径,在AB的同一侧画弧,两弧的交点记为C,则C是线段AB垂直平分线上的一点.请你利用类似的方法确定另一点D。
因为画图可知AC=BC,所以点C在线段AB的垂直平分线上;又AD=BD,所以点D也在线段AB的垂直平分线上;根据两点确定一条直线,所以直线CD就是线段AB的垂直平分线。
四、试一试
1、如图,点C在直线上,试过点C画出直线的垂线。
提示:能否利用画线段垂直平分线的方法解决呢?
请同学们把你的作法在小组内交流,请一些同学上台展示其画图过程、画图的作法,并说明画图的依据。
作法:
(1)以C为圆心,任一线段的长为半径画弧,交l于A、B两点;
(2)分别以A、B两点为圆心,以大于长为半径画弧,两弧相交于C、D两点;
(3)过C、D两点作直线CD。
所以,直线CD就是所求作的。
理由:以C为圆心,任一线段的长为半径画弧,交l于A、B两点,则C是线段AB的中点.因此,过C画直线l的垂线转化为画线段AB的垂直平分线。
2、如图,如果点C不在直线上,试和同学讨论,应采取怎样的步骤,过点C画出直线的垂线?
请同学们把讨论结果上台展示。
作法:
(1)任取一点M,使点M和点C在的两侧;
(2)以C点为圆心,以CM长为半径画弧,交于A、B两点;
(3)分别以A、B两点为圆心,以大于长为半径画弧,两弧相交于D点;
(4)过C、D两点作直线CD。
所以,直线CD就是所求作的。
你能否用所学的知识证明这个结论呢?试试看。
证明:连结CA、CB、DA、DB,设CD、AB相交于O。
由作法知,,,CD是公共边,
所以△CAD≌△CBD(SSS)
所以(全等三角形的对应角相等)
于是△ACO≌△BCO(SAS)
所以AO=BO,(全等三角形的对应边、对应角相等)
所以CD是线段AB的垂直平分线。
五、练一练
P102 练习1、2
六、说一说
1、本节你有何收获?
2、本节你有何体会?
3、本节你有何疑惑?
七、作业
P103 习题24.6 4、5
课题 :24.4.4 尺规作图(4)画角平分线
教学目标:
1、使学生掌握画角平分线的作法;
2、进一步训练学生用规范的语言叙述尺规作图的动作,达到作图准确,叙述正确;
3、掌握利用基本作图作一些其他图形。
重点难点:
重点:让学生掌握画角平分线的作法;
难点:利用基本作图画一些其他图形。
教学过程:
一、复习
1、尺规作图的工具是 ;
2、尺规作图时,直尺的作用是画 、 、 ,圆规的作用是画圆的 ;
3、看图填空。
(1)在 上截取 = = ;
(2)以 为圆心,以 为半径作弧,交 于 。
(3)分别以 、 为圆心,以大于的长为半径作弧,两弧交于 、 ;
(4)以O为圆心,以任意为半径作弧,分别交的两边OA、OB于 、 。
(1) (2) (3) (4)
4、填空:
(1)求作一个角等于已知角,
作法:(1)作 ;
(2)以O为圆心,以 作弧,交 ;交 ;
(3)以为圆心,以 作弧,交 ;
(4)以 为圆心,以 半径作弧,交 ;
(5)经过 作 。则 即为所求的角。
5、如图,△ABC中,为钝角,求作:AB上的高CD。
作法:(1)以 为圆心,适当长为半径作弧交直线AB于 ;
(2)分别以 为圆心,大于 的长为半径作弧,两弧相交于 ;
(3) 作直线交AB于 ,则CD为所求的高。
6、求作线段MN的垂直平分线。
作法:(1) 为圆心, 为半径作弧,两弧相交于 ;
(2)作 AB;
则 线段MN的垂直平分线。
二、新授
1、做一做:利用直尺和圆规把一个角二等分。
观察右图,所画的射线OC是的角平分线,你能根据图中的作图痕迹,你能画一个角的角平分线并写出画图步骤吗?动手试试。
请一些同学上台展示成果。
作法:(1)以O点为圆心,以任意长为半径,交角的两边于A、B两点;
(2)分别以A、B两点为圆心,以大于长为半径画弧,画弧交于C点;
(3)过C点作射线OC。
所以,射线OC就是所求作的。
问:你能用所学的知识来说明所画的射线OC是的角平分线吗?小组里交流讨论后发表看法。
因为由画图可知:,,OC又是公共边,
根据三角形全等的识别(SSS),可得△OBC≌△OAC,
由全等三角形的对应边相等、对应角相等可知:
于是OC是的角平分线。
2、试一试:试把右图所示的角四等分
请完成操作写出画法。小组里相互交流,老师巡视。
三、巩固练习
课本P103 练习1、2
四、联系知识综合运用
1、范例
已知:两条线段、
求作:直角三角形ABC使直角的平分线等于,一直角边
分析:要想用尺规画出满足条件的图形,首先画出草图,从草图可知,△ADB可以确定,而C点是在过A点垂直AB的直线上,又在BD的延长线上,所以其交点就是C点,那么就确定了△ABC。
作法:(1)画线段AB;
(2)过A点作;
(3)作的角平分线AN;
(4)在射线AN上截取;
(5)连结BD并延长交射线AM于C点;
△ABC就是所求作的。
请你说说对这种画图方法,你是如何理解的。
2、练习
已知:角,线段。
求作:等腰三角形△ABC,使其顶角,平分线。
五、说一说
说说本节你的收获、体会、疑惑。
六、作业
P103 习题24.4 5
课题 :24.5.1 回顾与思考(1)
教学目标:
1、梳理所学的知识,进一步体会图形全等以及三角形全等的特征与识别;
2、进一步培养学生的知识分类能力、观察图形能力;
3、掌握有关的识别和特征,熟练地应用于判断、计算和说理。
重点难点:
重点:熟练地应用三角形的识别和特征进行有关的计算与说理;
难点:进行严密地推理。
教学过程:
一、说一说
1、对于§24.1--§24.2你学了哪些知识,并把这些知识理清。请一些同学说说见解。
知识结构图供参考
2、什么是全等图形?
3、全等图形的识别的方法是什么?
4、全等图形的特征是什么?
5、三角形全等有什么特征?
6、如何识别两个三角形全等?
7、如何识别两个直角三角形全等?
二、体会
1、体会读图、分析图形的能力。
问题1:如图,你能找到几个三角形?如果△AED≌△BEC,那么
它们的对应边、对应角是什么?这时图中还有没有其他全等三角形?
(有五个三角形,如果△AED≌△BEC,那么△DAB≌△CBA)
问题2:连结C、D两点,添了一条线段又多了多少个三角形呢?又有多少全等三角形呢?
问题3:观察下列图形,说说哪些三角形可能全等?
做完这些问题后有何体会?
(1)有公共边的两个三角形可能全等。
(2)有公共角或对顶角的两个三角形也可能全等。
2、体会分析
问题4:如图,AB=AC,D、E分别在AB、AC上,BC、CD相交于O,,试说明BD=CE。
分析:(1)
(2)
(3)△ADC≌△AEB
你能否把老师的分析用图表的形式来表示出来吗?
3、体会推理论证和书写过程。
请同学把上题的分析过程书写出来,你有何体会呢?
(通过三角形全等,可以得到线段和角的相等,有的题目通过说明一对三角形全等就可以得出结论,而有的题目,为了说明一对三角形全等,还要说明另一对三角形全等。)
三、做一做
1、如图,要识别△ABC≌△ADE,除公共角外,把还需要的两个条件及其根据写在横线上。
(1) , (SAS)
(2) , ( )
(3) , ( )
(4) , ( )
(5) , ( )
(6) , ( )
(7) , ( )
2、如图,D为BC中点,,且,与相等吗?为什么?
3、如图,AB=AC,BD、CE是△ABC的角平分线,△ABD≌△CBE吗?为什么?
4、如图,AB=AD,AC=AE,,△ABC与△ADE全等吗?
四、小结
通过本节学习,你有何体会?
五、作业
P106 复习题1、2、3、4
课题 :24.5.2 回顾与思考(2)
教学目标:
1梳理知识,掌握定义、命题、定理、公理与证明、尺规作图的基本知识和基本技能,培养主动参与、合作交流、进一步提高分析、概括能力;
2、能灵活运用所学的知识,进一步拓展知识。
重点难点:
重点:梳理知识、巩固基本知识和基本技能;
难点:灵活运用所学知识解决问题。
教学过程:
一、说一说,梳理本章知识
1、理清§24.3--§24.4的知识。
命题与证明定义、命题、公理证明
2、男、女生竞赛
男、女生轮流回答下列问题,相互指导,回答正确与指导有意义一次各10分,分数高者胜,按男、女顺序回答,回答不来1人次扣2分。
(1)什么是定义?
(2)什么命题?
(3)什么是公理?
(4)什么是定理?
(5)什么是证明?
(6)上台画线段等于已知线段。
(7)画角等于已知角。
(8)画一条直线的垂线。
(9)画一条线段的垂直平分线。
(10)画一个角的角平分线。
二、做一做,拓展知识
1、下列语句是命题吗?
(1)画一个角等于两个已知角的和;
(2)钝角总大于直角;
(3)过点A作直线AB∥CD;
(4)相等并且互补的两个角是直角。
2、判断下列命题是真命题还是假命题,若假命题,则举一个反例说明:
(1)两直线平行,同旁内角互补;
(2)垂直于同一条直线的两直线平行;
(3)相等的角是内错角;
(4)有一个角是的三角形是等边三角形。
3、命题“互补的角互为邻补角”,写成如果 ,那么 。
4、已知:如图,,AE=AD,求证:AB=AC。
5、两个直角三角形有一个角及一条边分别对应相等,这两个直角三角形全等吗?试列出各种情况,并一一加以分析。
6、(1)用直尺作法有:
①过点 ,点 ,作直线 ;
②连结两点
③延长 到点 ;
④延长 到点 ,使 = 。
(2)用圆规作法有:
①在 上截取 = ;
②以点 为圆心 为半径作弧;
③以点 为圆心 为半径作弧交 于点 ;
④分别以点 ,点 为圆心 为半径作弧,两弧交于点 。
(3)用到基本作图时:
①作线段 = ;
②作 = ;
③作射线 平分 ;
④过点 作 ⊥ ,垂足是 ;
⑤作线段 的垂直平分线。
试着画一个四边形,使它的面积等于已知三角形的面积的2倍,并写出画法。
三、小结
谈谈本节你有何收获。
四、作业
复习题7、8、9、10单元测试
一、填空题:
1、如图,已知AF∥EC,AB∥CD,∠A=70°,则∠C= 度。
(1) (2)
2. 如图:已知BE∥CF,∴∠2=∠3( );又 ∵∠1=∠4(已知),
∴∠1+∠2=∠3+∠4,即∠ABC=∠DCB∴ AB ∥CD( )
3. 如图, AB=AC,∠1=∠2,AD=AE,则BD= ,∠BAE= °
(3) (4)
4.若AB∥CD,∠A=35°,∠C=45°,则∠E= 度。(过E作AB的平行线)。
5. 如图,已知∠AFE=∠ABC,DG∥BE,∠DGB=130°,则∠FEB= 度。
(5) (6) (7)
6.已知点B、A、D在同一直线上,AE∥BC,∠1=150°,∠c=70°,则∠B= 度,
∠2= 度。
7. 如图,直线AB、CD被EF所截,已知∠1=∠2,求证:AB∥CD。
证明:∵∠2=∠3,( ),∠1=∠2(已知) ∴ ∠1=∠3∴ AB∥CD( ) 8.①、命题“对顶角相等”,改写成“如果……,那么……”的形式: 。题设是 ,结论是 。
②、两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行,
题设是 ;结论是 。
③、等角的补角相等,题设是 ,结论是 。
9、如图,直线AB上有一点O,过O点作射线OD、OC、OE,且OC、OE分别是∠BOD和∠AOD的平分线,则∠1与∠2的大小关系是 ,∠1+∠3= 度,OC与OE的位置关系是 。
10. 如图,ΔABC中,AB=AC=4,P是BC上任意一点,过P作PD⊥AC于D,PE⊥AB于E,若SΔABC=6,则PE+PD= 。
(9) (10) (11)
11、如图,已知∠ACB=∠BDA=90°,要使△ACB≌△BDA,至少还需加上条件: 。
12、如图, △ABC≌△ADE,∠B=35°,∠EAB=21°,∠C=29°,则∠D= ° ,∠DAC= °
13、如图、在正方形网格上有一个ΔABC,①、作一个与它全等的三角形。②、如每一个小正方形的边长为1,则ΔABC的面积是:
二、选择题:
1、下列给出的四组条件中,能判定△ABC≌△DEF的是( ).
A.AB=DE,BC=EF, ∠A=∠D; B.∠A=∠D, ∠C=∠F,AC=EF;
C.∠A=∠D,∠B=∠E,∠C=∠F;
D、AB=DE, BC=EF, △ABC周长=△DEF周长
2.如图,D在AB上,E在AC上,且∠B=∠C,那么补充
下列一个条件后,仍无法判定△ABE≌△ACD的是( ).
A.AD=AE. B.∠AEB=∠ADC. C.BE=CD. D.AB=AC.
3. 若△ABC≌△DEF,且△ABC的周长为20,AB=5,BC=8,则DF长为( ).
A.5; B.8; C.7; C.5或8.
4. 下列各条件中,不能作出唯一三角形的条件是( )
A. 已知两边和夹角 B. 已知两边和其中一条边所对的角
C. 已知两角和夹边 D. 已知两角和其中一角的对边
5. 求作点P,使P到三角形三边的距离相等的方法是( )
A. 作两边的中垂线的交点 B. 作两边上的高线的交点
C. 作两边上的中线的交点 D. 作两角平分线的交点
6. 命题① 邻补角互补;② 对顶角相等;③ 同旁内角互补;④ 两点之间线段最短;⑤直线都相等⑥任何数都有倒数;⑦若,则;⑧ 三角对应相等的两三角形全等 ⑨ 若∠A+∠A=90°,则∠A与∠B互余
其中真命题有( )
A. 1个 B. 2个 C. 3个 D. 4个
7、 有三条直线,若,,则与的位置关系( )
A. 平行 B. 垂直 C. 相交 D. 不确定
8、 两个角的两边分别平行,那么这两个角( )
A. 相等 B. 互补 C. 互余 D. 相等或互补
9、下列语句中:① 同角的补角相等;② 雪是白的;③ 画∠AOB=∠?④ 他是小张吗?⑤两直线相交只有一个交点。其中是命题的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
10、 下列说法正确的是( )
A. 只要有两边对应相等,再有一角对应相等,则这两个三角形全等
B. 如图,∠1=∠2,则m∥n的理由是“两直线平行,内错角相等”
C. 如图,若AB=CD,BC=DA,那么∠B=∠D
D. 已知三条线段的长,能画出一个三角形
11、 如图,已知AD∥BC,AE平分∠DAB,BE平分∠ABC,则∠E( )
A. 大于90° B. 等于90° C. 小于90° D. 无法确定
12、 下列命题中,是假命题的是( )
A. 全等三角形对应边上的高线相等 B. 绝对值等于本身的数是正数
C. 同位角相等,两直线平行 D. 若a=0,则ab=0
13、如图,AB∥CD,∠1=100°,∠2=130°,则∠3的度数为( )
A.50° B. 65° C. 40° D. 45°
14、如图,ΔABC中,∠A=50°,BO、CO分别是∠ABC、∠ACB的平分线,则∠BOC的度数是( )
A. 115° B. 110° C. 105° D. 130°
三、将下列命题改写成“如果……,那么……”的形式。
1. 平行于同一条直线的两直线平行。
改:
2. 互为相反数的两数它们的绝对值相等。
改:
3. 两条互相垂直的直线夹角为直角。
改:
四、尺规作图:(不写作法,保留作图痕迹)
1、 如图,已知∠MON,求作射线OP,使∠MOP=∠NOP
2、已知:线段a,b求作:⊿ABC,使AB=AC,BC=a ,高AD=b
3、已知:线段a和∠,求作:△ABC,使BC=a,∠BCA=∠。
4、求作ΔABC外接圆。
A
B C
5、已知:∠和线段,(如图4),求作:以∠为底角,为底边的等腰△ABC。
五、如图,已知∠1=∠2,AD=AB,求证:ΔABC≌ΔADC。
六、如图,若AD∥BC,AB∥CD,,,求的度数。
七、如图,已知AC⊥BD于C,CF=CD,BF的延长线交AD于点E,且AC=BC。求证:(1);(2)BE⊥AD。
八、如图,已知,求证:。
九、已知,如图DE // BF,BE // DF,AD // BC,AB // DC,求证:(1),(2)
十、如图2,ABCD是正方形,点E在BC上,DF⊥AE于F,请你在AE上确定一点G,使△ABG≌△DAF,并给予证明。
十一、已知:如图7,CE⊥AB与E,BD⊥AC于D,BD、CE、AO交于点O,且AO平分∠BAC
求证:OB=OC
十二、如图,BE⊥AE,CF⊥AE,垂足分别是E、F,D是EF的中点,△BED与△CFD全等吗?为什么?
十三、已知△ABC中,∠C = 90°,沿过B的一条直线BE折叠这个三角形,使点C与AB边上的一点D重合。如图所示。要使D恰为AB的中点,还应添加一个什么条件?(请你写出三种不同的添加条件)选择(1)中的某一个添加条件作为题目的补充条件,试说明其能使D为AB中点的理由。
解:(1)添加条件:①_____________;
②_______________;③________。
(2)说明:
十四、如图.AB=CD, ∠D=∠ECA, EC=FD,求证:AE=BF
十五、(6分)如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF交CD于点G,∠1=50,求∠2的度数。
十六、如图6.下面四个条件中,请你以其中两个为已知条件,第三个为结论,推出一个正确的命题(只需写出一种情况).①AE = AD ②AB = AC ③OB = OC ④∠B=∠C
十七、等腰梯形一底的中点对边的两个端点的距离会相等吗?若相等,请给出证明。若不相等,请说明理由。
十八、探究题
如图5,直线AB∥ED,求证:∠ABC+∠CDE=∠BCD。
图5
根据图中给出的作辅助线的3种方法,选择其中一种,写出证明过程。
