第6单元正比例和反比例常考易错检测卷(单元培优)-小学数学六年级下册苏教版(含解析)
文档属性
| 名称 | 第6单元正比例和反比例常考易错检测卷(单元培优)-小学数学六年级下册苏教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-30 11:27:12 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第6单元正比例和反比例常考易错检测卷(单元培优)-小学数学六年级下册苏教版
一、选择题
1.耕地总面积一定,每小时耕地面积和耕地小时数( )
A.成正比例 B.成反比例 C.不成比例 D.不成反比例
2.下列各式中(a、b均不为0),a和b成反比例的是( )
A.a×9= B.7a=4b C.a×﹣4÷b=0 D. =b
3.下面的说法中,正确的有( )句。
①一个正方体的棱长扩大2倍,它的表面积扩大4倍,体积扩大8倍。
②把4∶5的前项和后项同时增加5倍,比值不变。
③甲数的相当于乙数的,乙数与甲数的比值是。
④一根1米长的绳子,用去50%,还剩50%米。
⑤A=2×3×5,B=2×3×7,A和B的最小公倍数是210。
⑥时间一定,速度和路程成反比例关系。
A.2 B.3 C.4 D.5
4.如果4X=3Y,那么X与Y成( )
A.正比例 B.反比例 C.不成比例 D.无法判断
5.下面的数量关系不成正比例的是( )
A.平行四边形的底一定,它的面积与高
B.同一时刻.同一地点物体的高度和影子的长度
C.正方形的边长和它的周长
D.圆的半径和它的面积
6.两个相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的( )一定,这两种量就叫做成反比例的量.
A.和 B.差 C.积 D.比值
二、填空题
7.比例的前项一定,比的后项和比值成( )比例.
8.甲、乙、丙三入进行百米赛跑,甲到终点时,乙离终点5米,丙离终点10米,乙到终点时,丙离终点还有( )米。
9.下图表示一列动车行驶的时间和路程的关系,这列动车每小时行驶( )千米,路程和时间成( )比例。
10.小军坐汽车去上海旅游,他每过10分钟看一次里程表上的读数,结果记录如下:
时间 8:10 8:20 8:30 8:40 8:50 …
里程表读数(km) 31220 31235 31250 ? 31280 …
(1)如图所示,这辆汽车行驶的路程和时间成( )比例。
(2)照这样的速度,8:40时里程表上的读数是( )。
(3)如果8:50时他们离上海还有60千米,照这样的速度,他们到达上海的时间是( )。
11.如果a+a=b,a和b( )比例;如果=y,那么x与y成( )比例。
12.如果a与b成正比例,则x=( ),如果a与b成反比例,则x=( )。
a 6 2.4
b 10 x
三、判断题
13.分数的分子一定,分数值和分母成正比例。( )
14.“一只青蛙四条腿,两只眼睛,一张嘴;两只青蛙八条腿,四只眼睛,两张嘴,三只青蛙……那么青蛙的只数与腿的条数成正比例关系”。( )
15.正方体的棱长和体积成正比例. ( )
16.一本书的总页数一定,已读的页数和未读的页数成反比例. ( )
17.少先队员每人做好事的件数一定,做好事的总件数与做好事的少先队员人数成正比例。( )
四、计算题
18.解方程或比例。
12x-27=9 x-25%x= 7.5∶x=∶12
五、解答题
19.有一批煤,计划每天烧200千克,可以烧45天。改善炉灶后,每天可以少烧10%的煤。这批煤可以烧多少天?
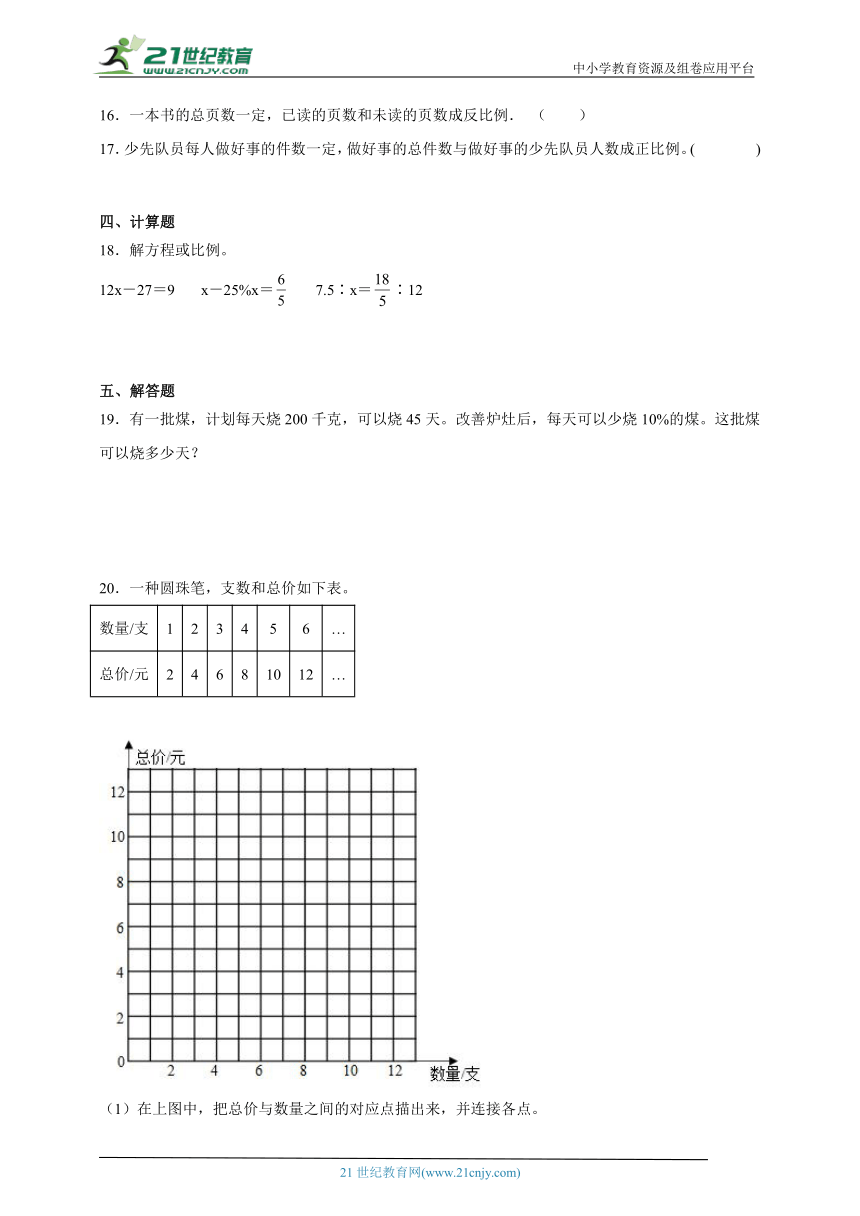
20.一种圆珠笔,支数和总价如下表。
数量/支 1 2 3 4 5 6 …
总价/元 2 4 6 8 10 12 …
(1)在上图中,把总价与数量之间的对应点描出来,并连接各点。
(2)总价与数量之间成什么比例关系?为什么?
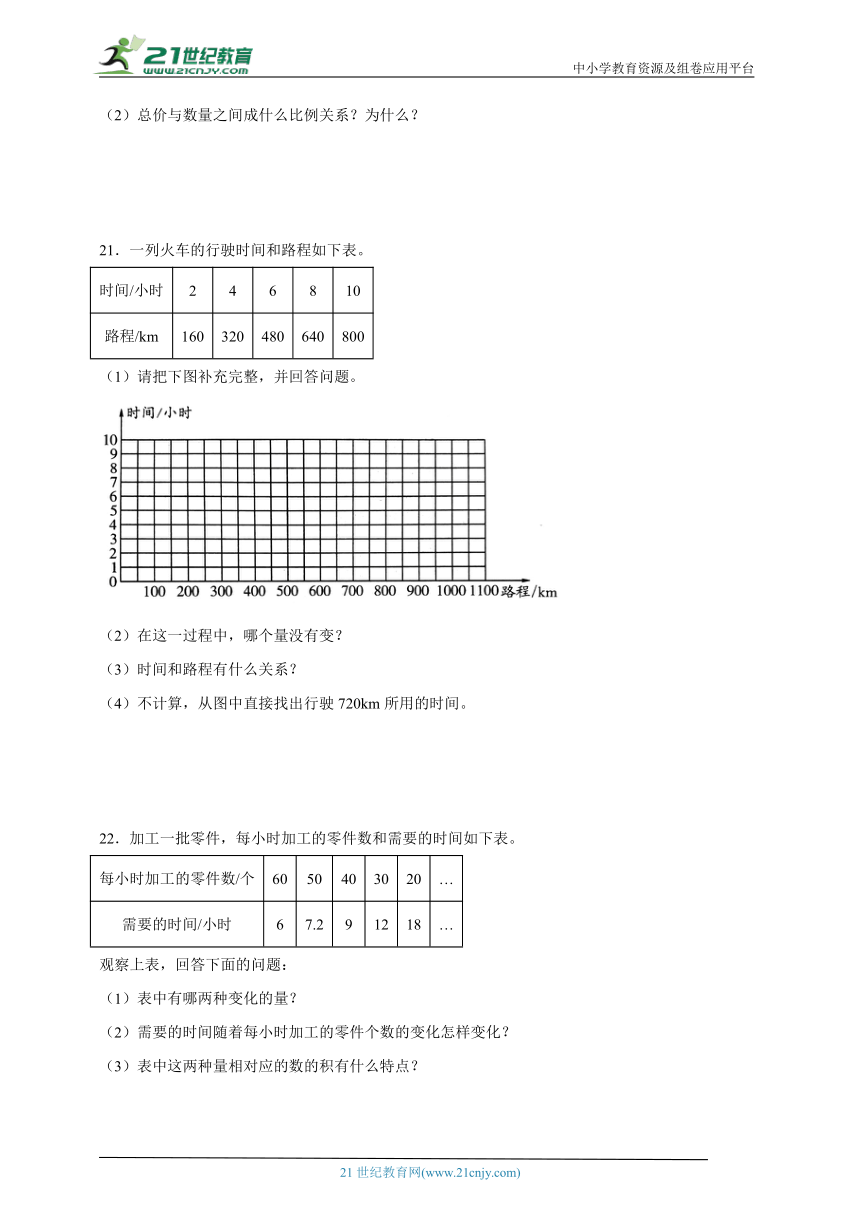
21.一列火车的行驶时间和路程如下表。
时间/小时 2 4 6 8 10
路程/km 160 320 480 640 800
(1)请把下图补充完整,并回答问题。
(2)在这一过程中,哪个量没有变?
(3)时间和路程有什么关系?
(4)不计算,从图中直接找出行驶720km所用的时间。
22.加工一批零件,每小时加工的零件数和需要的时间如下表。
每小时加工的零件数/个 60 50 40 30 20 …
需要的时间/小时 6 7.2 9 12 18 …
观察上表,回答下面的问题:
(1)表中有哪两种变化的量?
(2)需要的时间随着每小时加工的零件个数的变化怎样变化?
(3)表中这两种量相对应的数的积有什么特点?
23.小红中午在家门口测量一棵树的高度时发现,这棵树在阳光下的影长是2.5米,同一时间,同一地点,测得一根直立在地面上,长为2米的竹竿的影长是0.5米,这棵树高多少?
24.甲、乙两个长方形容器的底面都是正方形,且底面周长之比是2∶3。将甲容器盛满水,再将水全部倒入乙容器,乙容器的水面高16厘米,则甲容器的高是多少厘米?
参考答案:
1.B
【分析】耕地总面积一定,先判断每小时耕地面积和耕地小时数的商一定还是乘积一定,如果商一定就成正比例,如果乘积一定就成反比例,否则不成比例.
【详解】每小时耕地面积×耕地小时数=耕地总面积(一定),每小时耕地面积与耕地小时数的乘积一定,二者成反比例.
故答案为B
2.C
【分析】根据反比例的意义a×b=k(一定),先将各个等式按比例的基本性质改写,即可作出选择.
【详解】解:A、由a×9=得出a:b=:9=,a和b成正比例;
B、由7a=4b得出a:b=4:7=,a和b成正比例;
C、a×﹣4÷b=0得出ab=12,a和b成反比例;
D、=b得出a+7=10b,a和b不成比例;
故选C.
【点评】此题主要考查分比例的意义及比例的基本性质.
3.C
【分析】①根据正方体表面积扩大的倍数是棱长扩大倍数的平方,体积扩大的倍数是棱长扩大倍数的立方。②比的前项和后项同时乘或除以同一个数(0除外),比值不变。③根据甲数×=乙数×,可求出乙数与甲数的比值是多少。④百分数表示的是一个数占另一个数的百分之几,也叫百分率或百分比,百分数后面不能带单位。⑤根据求最小公倍数的方法,用两个数公有质因数和独有质因数的乘积进行解答。⑥路程÷速度=时间(一定),路程和速度的比值一定,成正比例关系。
【详解】由分析可知:
①一个正方体的棱长扩大2倍,它的表面积扩大4倍,体积扩大8倍,正确。
②把4∶5的前项和后项同时增加5倍,比值不变,正确。
③根据甲数×=乙数×,可求出乙数与甲数的比值:÷=,正确。
④百分数后面不能带单位,所以一根1米长的绳子,用去50%,还剩50%米,错误。
⑤A=2×3×5,B=2×3×7,A和B的最小公倍数是:2×3×5×7=210,正确。
⑥路程÷速度=时间(一定),路程和速度的比值一定,成正比例关系。所以时间一定,速度和路程成反比例关系不正确。
故答案为:C
【点睛】本题是道综合题,应对立体几何、比的应用、百分数的认识、正比例反比例等知识综合应用。
4.A
【分析】根据判断两种量成正比例还是成反比例的方法:关键是看这两种相关联的量中相对应的两个数的商一定还是积一定,如果商一定,就成正比例关系;如果积一定,就成反比例关系;进行解答即可.
【详解】因为4x=3y,则=(一定),
所以y和x成正比例;
故选A.
5.D
【分析】根据判断两种量成正比例的方法:关键是看这两种相关联的量中相对应的两个数的比值是否是一定,如果比值一定,就成正比例关系;否则就不成正比例.据此对各项进行分析,进而得出结论.
【详解】A、因为平行四边形的面积÷高=底(一定),是比值一定,所以成正比例;
B、因为同一时刻,同一地点物体的高度和影子的长度的比值一定,所以成正比例;
C、因为正方形的周长÷边长=4(一定),所以成正比例;
D、因为圆的面积÷半径=圆周率×半径(不一定),所以不成正比例.
故选D.
6.C
【详解】略
7.反
【详解】比例的后项×比值=比例的前项,前项一定,所以比的后项和比值成反比例.
8.
【分析】根据速度×时间=路程可知,时间一定时,路程和速度成正比,速度之比=路程之比,甲到终点时,乙和丙跑的路程分别是100-5=95米,100-10=90米,则甲乙的速度之比=95∶90,因为速度比是不变的,所以可以设乙到终点时,丙离终点还有x米,则乙跑了5米的时间内,丙跑了10-x米,进而求出乙、丙的速度比=5∶(10-x),据此列出方程:(100-5)∶(100-10)=5∶(10-x),再依据比例的基本性质求出x的值即可。
【详解】解:设乙到终点时,丙离终点还有x米
(100-5)∶(100-10)=5∶(10-x)
95∶90=5∶(10-x)
950-95x=450
95x=500
x=
所以乙到终点时,丙离终点还有米。
【点睛】依据速度之比不变的规律,找准等量关系式并依据等量关系式列出方程是解题的关键,时间一定时,路程和速度成正比,速度之比=路程之比。
9. 5 正
【分析】根据图示可知横轴表示时间,纵轴表示路程,根据路程=速度×时间,速度=路程÷时间,可知这列动车每小时行驶5÷1=5千米;两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。据此解答。
【详解】5÷1=5(千米)
因为路程变化时间也随着变化,而且路程与时间的比值一定,所以路程与时间成正比例。
【点睛】此题考查的是正比例的辨识,解题时注意时间、速度和路程三者之间的关系。
10. 正 31265 9:30
【分析】(1)根据表格数据可知,汽车每10分钟行驶的路程都是15千米,路程与时间的比值即速度是定值1.5,可知这辆汽车行驶的路程和时间成正比例;
(2)从8:30到8:40经过10分钟,8:30时里程表上的读数加上15千米即为8:40时的里程表上的读数;
(3)用60千米除以汽车的速度得出还需要的时间,8:50再加上这个时间即为到达上海的时间。
【详解】(1)(31235-31220)∶(8:20-8:10)=15∶10=1.5
(312350-31235)∶(8:30-8:20)=15∶10=1.5
路程与时间的比值即速度相等,所以这辆汽车行驶的路程和时间成正比例。
(2)从8:30到8:40经过10分钟,
31250+15=31265(千米)
照这样的速度,8:40时里程表上的读数是31265。
(3)60÷1.5=40(分钟)
8时50分+40分钟=9:30
他们到达上海的时间是9:30。
故答案为:正;31265;9:30
【点睛】判断两种量成正比例的方法:关键是看这两个相关联的量中相对的两个数的比值,如果比值一定,就成正比例。
11. 正 反
【分析】判断两种相关联的量成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例。
【详解】如果a+a=b,那么2a=b,=2,比值一定,a和b成正比例;
如果=y,,那么xy=8,乘积一定,x与y成反比例。
故答案为:正;反
【点睛】掌握判断两种相关联的量是否成正、反比例的方法是解答此题的关键。
12. 4 25
【分析】如果a和b成正比例,说明a和b的比值一定,再根据比值一定列出比例式,进而根据比例的性质,解比例得解;
如果a和b成反比例,说明a和b的乘积一定,再根据乘积一定列出比例式,进而根据比例的性质,解比例得解。
【详解】如果a和b成正比例,那么
6∶10=2.4∶x
6x=10×2.4
x=24÷6
x=4;
如果a与b成反比例,那么
2.4x=6×10
x=60÷2.4
x=25
故答案为:4;25
【点睛】解决此题关键是根据比值一定或乘积一定,先列出比例,进而根据比例的性质先把比例式转化为乘积式来解比例得解。
13.×
【详解】分数的分数值和分母是两种相关联的量,分数值×分母=分子(一定),它们的乘积一定,而不是比值一定,所以不成正比例。
14.√
【分析】判断两种量成不成比例,成什么比例,就看这两种量是否是①相关联;②一种量变化,另一种量也随着变化,变化方向相同或相反;③对应的比值或乘积一定;如果这两种量相关联的量都是变量,且对应的比值一定,就成正比例;如果两种量相关联的量都是变量,且对应的乘积一定,就成反比例;如果是其它的量一定或乘积、比值不一定,就不成比例。
【详解】因为青蛙的腿的条数:只数=4∶1=8∶2=4(一定),是青蛙的腿的条数与只数对应的比值一定,所以青蛙的只数与腿的条数成正比例关系;
故判断为:√
【点睛】此题属于根据正、反比例的意义,辨识两种相关联的量成不成比例,成什么比例,就看这两种量是否都是变量,且对应的比值一定,或是对应的乘积一定,再做出判断。
15.×
【详解】略
16.错误
【详解】略
17.√
【分析】判定两种相关联的量是否成正、反比例,要看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定就成正比例;如果是乘积一定就成反比例。
【详解】做好事的总件数÷做好事的少先队员人数=每人做好事的件数(一定),是比值一定,所以成正比例。
故答案为:√
18.x=3;x=;x=25
【分析】12x-27=9,先算9+27,再用9+27的和除以12,即可解答;
x-25%x=,先算出1-25%=75%,再用除以75%,即可解答;
7.5∶x=∶12,解比例,原式变为:x=7.5×12,再用7.5×12的积除以,即可解答。
【详解】12x-27=9
解:12x=9+27
12x=36
x=36÷12
x=3
x-25%x=
解:75%x=
x=÷75%
x=÷
x=×
x=
7.5∶x=∶12
解:x=7.5×12
x=90
x=90÷
x=90×
x=25
19.50天
【分析】先求出煤的总重量,再求出改善炉灶之后每天烧的煤的重量,用总量除以改善炉灶后每天烧的煤的重量,就是烧的天数。
【详解】200×45÷(200-200×10%)
=9000÷180
=50(天)
答:这批煤可以烧50天。
【点睛】根据这批煤的总量不变建立等量关系是本题的关键。
20.(1)
(2)成正比例关系;比值一定
【分析】(1)根据表格中总价和数量的一一对应关系,在图中描点并连线。
(2)两个相互关联的量,如果它们的比值是一定的,则这两个量是正比例关系。总价=单价×数量,由此求解。
【详解】(1)总价和数量的关系在图中应是一条平滑的直线关系。
(2),比值一定,符合正比例定义,所以总价和数量成正比例关系。
【点睛】掌握总价和数量之间关系以及正比例关系的定义是解决问题的关键。
21.(1)
(2)速度
(3)路程随着时间的增加而增加成正比例关系
(4)9小时
【分析】(1)根据表格中总价和数量的一一对应关系,在图中描点并连线。
(2)根据表格可知,速度一直是没有改变的。
(3)路程=速度×时间。两个相互关联的量,如果它们的比值是一定的,则它们的关系是正比例关系。
(4)在图中,找准720km所对应的时间。
【详解】(1)路程和时间的关系在图中应是一条平滑的直线关系。
(2)速度一直没有改变为:80km/h。
(3)路程随着时间的增加而增加成正比例关系。
(4)由图可知,行驶720km所用的时间为9小时。
【点睛】在掌握正比例与反比例概念的基础上,对价格公式进行变形,确定相关联的量的数量关系。
22.(1)每小时加工的零件数和需要的时间;
(2)需要的时间随着每小时加工的零件个数的增加而减少;
(3)表中这两种量的相对应的数的积都是360。
【分析】(1)根据表格中最左列可知表中表示每小时加工的零件数与需要的时间两种变化的量。
(2)每小时加工的零件数从60逐渐减少到20,需要的时间由6小时增加到18小时。
(3)根据题中这两种量相对应的数计算乘积,60×6=360,50×7.2=360,40×9=360……
【详解】根据分析可知:
(1)每小时加工的零件数和需要的时间是两种变化的量。
(2)需要的时间随着每小时加工的零件个数的增加而减少。
(3)60×6=360,50×7.2=360,40×9=360……可得到表中这两种量的相对应的数的积都是360。
【点睛】主要考查分析表格的能力,根据题中信息进行综合分析解答。
23.10米
【分析】根据题意知道,同一时间,同一地点测得物体的高度与影子的长度的比值一定,即物体的高度与影子的长度成正比例,由此先假设出这棵树在地面上的影子对应的树的实际高度,根据比例关系,列出比例求出地面上的影子对应的树的高度。
【详解】解:设这棵树高x米。
2.5∶x=0.5∶2
0.5x=5
x=10
答:这棵树高10米。
【点睛】明确同一时间,同一地点测得物体的高度与影子的长度的比值一定是解决本题的关键。
24.36厘米
【分析】由底面周长之比是2∶3;可知底面面积之比是4∶9;因为水的体积是一定的,所以底面积与高成反比例关系,设甲容器的高是x厘米,那么4x=9×16;由此进行解答
【详解】解:设甲容器的高是x厘米,由题意及分析可得:
4x=9×16
解得x=36
答:甲容器的高是36厘米。
【点睛】解答本题的关键是理解正方形周长之比各自的平方等于面积之比。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第6单元正比例和反比例常考易错检测卷(单元培优)-小学数学六年级下册苏教版
一、选择题
1.耕地总面积一定,每小时耕地面积和耕地小时数( )
A.成正比例 B.成反比例 C.不成比例 D.不成反比例
2.下列各式中(a、b均不为0),a和b成反比例的是( )
A.a×9= B.7a=4b C.a×﹣4÷b=0 D. =b
3.下面的说法中,正确的有( )句。
①一个正方体的棱长扩大2倍,它的表面积扩大4倍,体积扩大8倍。
②把4∶5的前项和后项同时增加5倍,比值不变。
③甲数的相当于乙数的,乙数与甲数的比值是。
④一根1米长的绳子,用去50%,还剩50%米。
⑤A=2×3×5,B=2×3×7,A和B的最小公倍数是210。
⑥时间一定,速度和路程成反比例关系。
A.2 B.3 C.4 D.5
4.如果4X=3Y,那么X与Y成( )
A.正比例 B.反比例 C.不成比例 D.无法判断
5.下面的数量关系不成正比例的是( )
A.平行四边形的底一定,它的面积与高
B.同一时刻.同一地点物体的高度和影子的长度
C.正方形的边长和它的周长
D.圆的半径和它的面积
6.两个相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的( )一定,这两种量就叫做成反比例的量.
A.和 B.差 C.积 D.比值
二、填空题
7.比例的前项一定,比的后项和比值成( )比例.
8.甲、乙、丙三入进行百米赛跑,甲到终点时,乙离终点5米,丙离终点10米,乙到终点时,丙离终点还有( )米。
9.下图表示一列动车行驶的时间和路程的关系,这列动车每小时行驶( )千米,路程和时间成( )比例。
10.小军坐汽车去上海旅游,他每过10分钟看一次里程表上的读数,结果记录如下:
时间 8:10 8:20 8:30 8:40 8:50 …
里程表读数(km) 31220 31235 31250 ? 31280 …
(1)如图所示,这辆汽车行驶的路程和时间成( )比例。
(2)照这样的速度,8:40时里程表上的读数是( )。
(3)如果8:50时他们离上海还有60千米,照这样的速度,他们到达上海的时间是( )。
11.如果a+a=b,a和b( )比例;如果=y,那么x与y成( )比例。
12.如果a与b成正比例,则x=( ),如果a与b成反比例,则x=( )。
a 6 2.4
b 10 x
三、判断题
13.分数的分子一定,分数值和分母成正比例。( )
14.“一只青蛙四条腿,两只眼睛,一张嘴;两只青蛙八条腿,四只眼睛,两张嘴,三只青蛙……那么青蛙的只数与腿的条数成正比例关系”。( )
15.正方体的棱长和体积成正比例. ( )
16.一本书的总页数一定,已读的页数和未读的页数成反比例. ( )
17.少先队员每人做好事的件数一定,做好事的总件数与做好事的少先队员人数成正比例。( )
四、计算题
18.解方程或比例。
12x-27=9 x-25%x= 7.5∶x=∶12
五、解答题
19.有一批煤,计划每天烧200千克,可以烧45天。改善炉灶后,每天可以少烧10%的煤。这批煤可以烧多少天?
20.一种圆珠笔,支数和总价如下表。
数量/支 1 2 3 4 5 6 …
总价/元 2 4 6 8 10 12 …
(1)在上图中,把总价与数量之间的对应点描出来,并连接各点。
(2)总价与数量之间成什么比例关系?为什么?
21.一列火车的行驶时间和路程如下表。
时间/小时 2 4 6 8 10
路程/km 160 320 480 640 800
(1)请把下图补充完整,并回答问题。
(2)在这一过程中,哪个量没有变?
(3)时间和路程有什么关系?
(4)不计算,从图中直接找出行驶720km所用的时间。
22.加工一批零件,每小时加工的零件数和需要的时间如下表。
每小时加工的零件数/个 60 50 40 30 20 …
需要的时间/小时 6 7.2 9 12 18 …
观察上表,回答下面的问题:
(1)表中有哪两种变化的量?
(2)需要的时间随着每小时加工的零件个数的变化怎样变化?
(3)表中这两种量相对应的数的积有什么特点?
23.小红中午在家门口测量一棵树的高度时发现,这棵树在阳光下的影长是2.5米,同一时间,同一地点,测得一根直立在地面上,长为2米的竹竿的影长是0.5米,这棵树高多少?
24.甲、乙两个长方形容器的底面都是正方形,且底面周长之比是2∶3。将甲容器盛满水,再将水全部倒入乙容器,乙容器的水面高16厘米,则甲容器的高是多少厘米?
参考答案:
1.B
【分析】耕地总面积一定,先判断每小时耕地面积和耕地小时数的商一定还是乘积一定,如果商一定就成正比例,如果乘积一定就成反比例,否则不成比例.
【详解】每小时耕地面积×耕地小时数=耕地总面积(一定),每小时耕地面积与耕地小时数的乘积一定,二者成反比例.
故答案为B
2.C
【分析】根据反比例的意义a×b=k(一定),先将各个等式按比例的基本性质改写,即可作出选择.
【详解】解:A、由a×9=得出a:b=:9=,a和b成正比例;
B、由7a=4b得出a:b=4:7=,a和b成正比例;
C、a×﹣4÷b=0得出ab=12,a和b成反比例;
D、=b得出a+7=10b,a和b不成比例;
故选C.
【点评】此题主要考查分比例的意义及比例的基本性质.
3.C
【分析】①根据正方体表面积扩大的倍数是棱长扩大倍数的平方,体积扩大的倍数是棱长扩大倍数的立方。②比的前项和后项同时乘或除以同一个数(0除外),比值不变。③根据甲数×=乙数×,可求出乙数与甲数的比值是多少。④百分数表示的是一个数占另一个数的百分之几,也叫百分率或百分比,百分数后面不能带单位。⑤根据求最小公倍数的方法,用两个数公有质因数和独有质因数的乘积进行解答。⑥路程÷速度=时间(一定),路程和速度的比值一定,成正比例关系。
【详解】由分析可知:
①一个正方体的棱长扩大2倍,它的表面积扩大4倍,体积扩大8倍,正确。
②把4∶5的前项和后项同时增加5倍,比值不变,正确。
③根据甲数×=乙数×,可求出乙数与甲数的比值:÷=,正确。
④百分数后面不能带单位,所以一根1米长的绳子,用去50%,还剩50%米,错误。
⑤A=2×3×5,B=2×3×7,A和B的最小公倍数是:2×3×5×7=210,正确。
⑥路程÷速度=时间(一定),路程和速度的比值一定,成正比例关系。所以时间一定,速度和路程成反比例关系不正确。
故答案为:C
【点睛】本题是道综合题,应对立体几何、比的应用、百分数的认识、正比例反比例等知识综合应用。
4.A
【分析】根据判断两种量成正比例还是成反比例的方法:关键是看这两种相关联的量中相对应的两个数的商一定还是积一定,如果商一定,就成正比例关系;如果积一定,就成反比例关系;进行解答即可.
【详解】因为4x=3y,则=(一定),
所以y和x成正比例;
故选A.
5.D
【分析】根据判断两种量成正比例的方法:关键是看这两种相关联的量中相对应的两个数的比值是否是一定,如果比值一定,就成正比例关系;否则就不成正比例.据此对各项进行分析,进而得出结论.
【详解】A、因为平行四边形的面积÷高=底(一定),是比值一定,所以成正比例;
B、因为同一时刻,同一地点物体的高度和影子的长度的比值一定,所以成正比例;
C、因为正方形的周长÷边长=4(一定),所以成正比例;
D、因为圆的面积÷半径=圆周率×半径(不一定),所以不成正比例.
故选D.
6.C
【详解】略
7.反
【详解】比例的后项×比值=比例的前项,前项一定,所以比的后项和比值成反比例.
8.
【分析】根据速度×时间=路程可知,时间一定时,路程和速度成正比,速度之比=路程之比,甲到终点时,乙和丙跑的路程分别是100-5=95米,100-10=90米,则甲乙的速度之比=95∶90,因为速度比是不变的,所以可以设乙到终点时,丙离终点还有x米,则乙跑了5米的时间内,丙跑了10-x米,进而求出乙、丙的速度比=5∶(10-x),据此列出方程:(100-5)∶(100-10)=5∶(10-x),再依据比例的基本性质求出x的值即可。
【详解】解:设乙到终点时,丙离终点还有x米
(100-5)∶(100-10)=5∶(10-x)
95∶90=5∶(10-x)
950-95x=450
95x=500
x=
所以乙到终点时,丙离终点还有米。
【点睛】依据速度之比不变的规律,找准等量关系式并依据等量关系式列出方程是解题的关键,时间一定时,路程和速度成正比,速度之比=路程之比。
9. 5 正
【分析】根据图示可知横轴表示时间,纵轴表示路程,根据路程=速度×时间,速度=路程÷时间,可知这列动车每小时行驶5÷1=5千米;两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。据此解答。
【详解】5÷1=5(千米)
因为路程变化时间也随着变化,而且路程与时间的比值一定,所以路程与时间成正比例。
【点睛】此题考查的是正比例的辨识,解题时注意时间、速度和路程三者之间的关系。
10. 正 31265 9:30
【分析】(1)根据表格数据可知,汽车每10分钟行驶的路程都是15千米,路程与时间的比值即速度是定值1.5,可知这辆汽车行驶的路程和时间成正比例;
(2)从8:30到8:40经过10分钟,8:30时里程表上的读数加上15千米即为8:40时的里程表上的读数;
(3)用60千米除以汽车的速度得出还需要的时间,8:50再加上这个时间即为到达上海的时间。
【详解】(1)(31235-31220)∶(8:20-8:10)=15∶10=1.5
(312350-31235)∶(8:30-8:20)=15∶10=1.5
路程与时间的比值即速度相等,所以这辆汽车行驶的路程和时间成正比例。
(2)从8:30到8:40经过10分钟,
31250+15=31265(千米)
照这样的速度,8:40时里程表上的读数是31265。
(3)60÷1.5=40(分钟)
8时50分+40分钟=9:30
他们到达上海的时间是9:30。
故答案为:正;31265;9:30
【点睛】判断两种量成正比例的方法:关键是看这两个相关联的量中相对的两个数的比值,如果比值一定,就成正比例。
11. 正 反
【分析】判断两种相关联的量成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例。
【详解】如果a+a=b,那么2a=b,=2,比值一定,a和b成正比例;
如果=y,,那么xy=8,乘积一定,x与y成反比例。
故答案为:正;反
【点睛】掌握判断两种相关联的量是否成正、反比例的方法是解答此题的关键。
12. 4 25
【分析】如果a和b成正比例,说明a和b的比值一定,再根据比值一定列出比例式,进而根据比例的性质,解比例得解;
如果a和b成反比例,说明a和b的乘积一定,再根据乘积一定列出比例式,进而根据比例的性质,解比例得解。
【详解】如果a和b成正比例,那么
6∶10=2.4∶x
6x=10×2.4
x=24÷6
x=4;
如果a与b成反比例,那么
2.4x=6×10
x=60÷2.4
x=25
故答案为:4;25
【点睛】解决此题关键是根据比值一定或乘积一定,先列出比例,进而根据比例的性质先把比例式转化为乘积式来解比例得解。
13.×
【详解】分数的分数值和分母是两种相关联的量,分数值×分母=分子(一定),它们的乘积一定,而不是比值一定,所以不成正比例。
14.√
【分析】判断两种量成不成比例,成什么比例,就看这两种量是否是①相关联;②一种量变化,另一种量也随着变化,变化方向相同或相反;③对应的比值或乘积一定;如果这两种量相关联的量都是变量,且对应的比值一定,就成正比例;如果两种量相关联的量都是变量,且对应的乘积一定,就成反比例;如果是其它的量一定或乘积、比值不一定,就不成比例。
【详解】因为青蛙的腿的条数:只数=4∶1=8∶2=4(一定),是青蛙的腿的条数与只数对应的比值一定,所以青蛙的只数与腿的条数成正比例关系;
故判断为:√
【点睛】此题属于根据正、反比例的意义,辨识两种相关联的量成不成比例,成什么比例,就看这两种量是否都是变量,且对应的比值一定,或是对应的乘积一定,再做出判断。
15.×
【详解】略
16.错误
【详解】略
17.√
【分析】判定两种相关联的量是否成正、反比例,要看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定就成正比例;如果是乘积一定就成反比例。
【详解】做好事的总件数÷做好事的少先队员人数=每人做好事的件数(一定),是比值一定,所以成正比例。
故答案为:√
18.x=3;x=;x=25
【分析】12x-27=9,先算9+27,再用9+27的和除以12,即可解答;
x-25%x=,先算出1-25%=75%,再用除以75%,即可解答;
7.5∶x=∶12,解比例,原式变为:x=7.5×12,再用7.5×12的积除以,即可解答。
【详解】12x-27=9
解:12x=9+27
12x=36
x=36÷12
x=3
x-25%x=
解:75%x=
x=÷75%
x=÷
x=×
x=
7.5∶x=∶12
解:x=7.5×12
x=90
x=90÷
x=90×
x=25
19.50天
【分析】先求出煤的总重量,再求出改善炉灶之后每天烧的煤的重量,用总量除以改善炉灶后每天烧的煤的重量,就是烧的天数。
【详解】200×45÷(200-200×10%)
=9000÷180
=50(天)
答:这批煤可以烧50天。
【点睛】根据这批煤的总量不变建立等量关系是本题的关键。
20.(1)
(2)成正比例关系;比值一定
【分析】(1)根据表格中总价和数量的一一对应关系,在图中描点并连线。
(2)两个相互关联的量,如果它们的比值是一定的,则这两个量是正比例关系。总价=单价×数量,由此求解。
【详解】(1)总价和数量的关系在图中应是一条平滑的直线关系。
(2),比值一定,符合正比例定义,所以总价和数量成正比例关系。
【点睛】掌握总价和数量之间关系以及正比例关系的定义是解决问题的关键。
21.(1)
(2)速度
(3)路程随着时间的增加而增加成正比例关系
(4)9小时
【分析】(1)根据表格中总价和数量的一一对应关系,在图中描点并连线。
(2)根据表格可知,速度一直是没有改变的。
(3)路程=速度×时间。两个相互关联的量,如果它们的比值是一定的,则它们的关系是正比例关系。
(4)在图中,找准720km所对应的时间。
【详解】(1)路程和时间的关系在图中应是一条平滑的直线关系。
(2)速度一直没有改变为:80km/h。
(3)路程随着时间的增加而增加成正比例关系。
(4)由图可知,行驶720km所用的时间为9小时。
【点睛】在掌握正比例与反比例概念的基础上,对价格公式进行变形,确定相关联的量的数量关系。
22.(1)每小时加工的零件数和需要的时间;
(2)需要的时间随着每小时加工的零件个数的增加而减少;
(3)表中这两种量的相对应的数的积都是360。
【分析】(1)根据表格中最左列可知表中表示每小时加工的零件数与需要的时间两种变化的量。
(2)每小时加工的零件数从60逐渐减少到20,需要的时间由6小时增加到18小时。
(3)根据题中这两种量相对应的数计算乘积,60×6=360,50×7.2=360,40×9=360……
【详解】根据分析可知:
(1)每小时加工的零件数和需要的时间是两种变化的量。
(2)需要的时间随着每小时加工的零件个数的增加而减少。
(3)60×6=360,50×7.2=360,40×9=360……可得到表中这两种量的相对应的数的积都是360。
【点睛】主要考查分析表格的能力,根据题中信息进行综合分析解答。
23.10米
【分析】根据题意知道,同一时间,同一地点测得物体的高度与影子的长度的比值一定,即物体的高度与影子的长度成正比例,由此先假设出这棵树在地面上的影子对应的树的实际高度,根据比例关系,列出比例求出地面上的影子对应的树的高度。
【详解】解:设这棵树高x米。
2.5∶x=0.5∶2
0.5x=5
x=10
答:这棵树高10米。
【点睛】明确同一时间,同一地点测得物体的高度与影子的长度的比值一定是解决本题的关键。
24.36厘米
【分析】由底面周长之比是2∶3;可知底面面积之比是4∶9;因为水的体积是一定的,所以底面积与高成反比例关系,设甲容器的高是x厘米,那么4x=9×16;由此进行解答
【详解】解:设甲容器的高是x厘米,由题意及分析可得:
4x=9×16
解得x=36
答:甲容器的高是36厘米。
【点睛】解答本题的关键是理解正方形周长之比各自的平方等于面积之比。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
