【倍速课时学练】(2014金秋开学)华师大版八年级数学上册《14.2勾股定理的应用》同步教学课件
文档属性
| 名称 | 【倍速课时学练】(2014金秋开学)华师大版八年级数学上册《14.2勾股定理的应用》同步教学课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-06-20 17:10:24 | ||
图片预览







文档简介
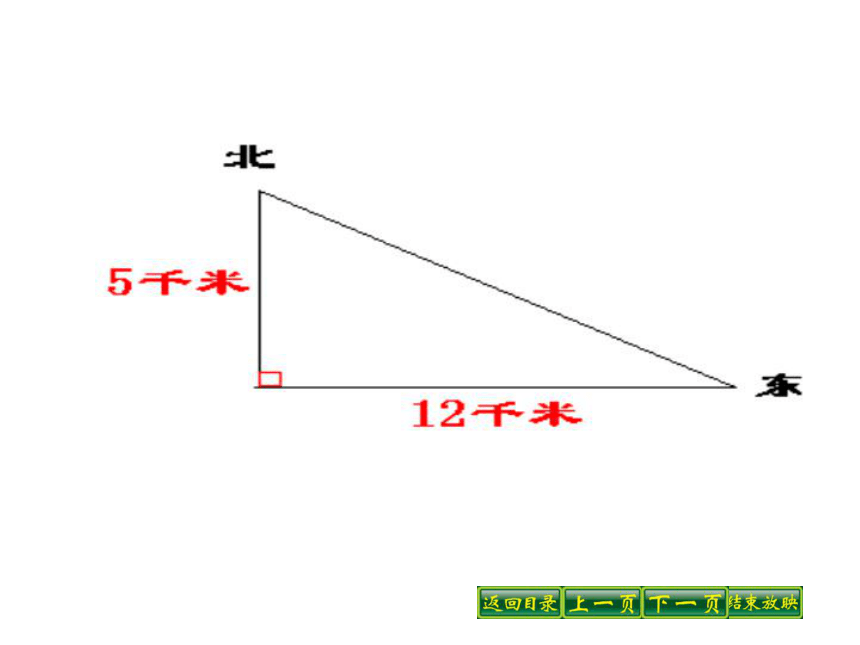
课件25张PPT。14.2勾股定理的应用 学习目标课堂小结巩固练习例题讲解学习六步曲探究新知回顾思考学习目标 1、明确解决路线最短问题的公理是两点之间,线段最短”,方法是将原来的曲面或多个平面展开成一个平面去解决.2、构造直角三角形,熟练应用勾股定理求出最短距离.1.甲、乙两位探险者到沙漠进行探险。某日早晨8:00甲先出发,他以6千米/时的速度向东行走。1时后乙出发,他以5千米/时的速度向北行进。上午10:00,甲、乙二人相距多远?
?
?
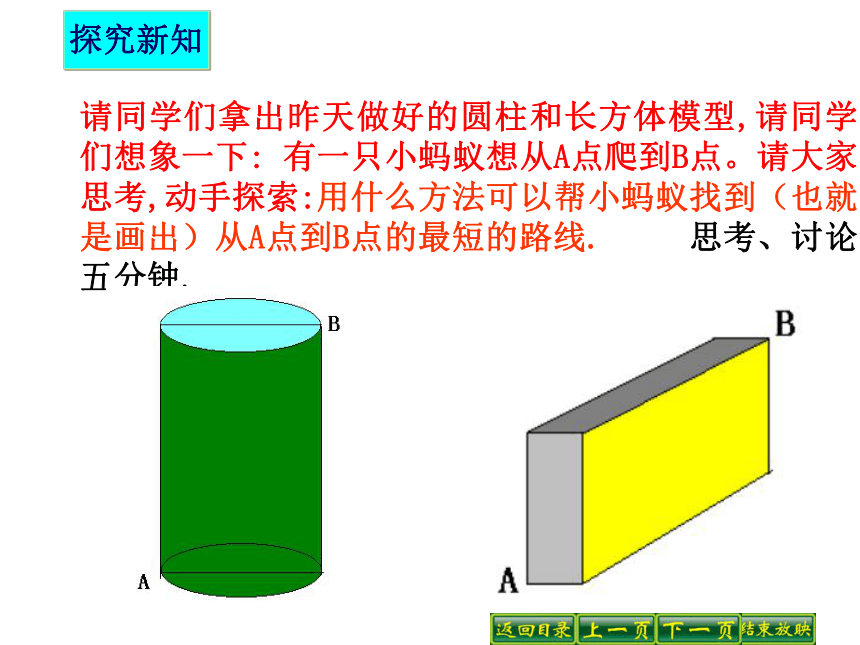
先根据题意画出图形,然后解题。回顾思考请同学们拿出昨天做好的圆柱和长方体模型,请同学们想象一下: 有一只小蚂蚁想从A点爬到B点。请大家思考,动手探索:用什么方法可以帮小蚂蚁找到(也就是画出)从A点到B点的最短的路线. 思考、讨论五分钟.探究新知引导语一:如果是一只飞蚂蚁,或鱼缸中的金鱼,则在空间中连接AB. 因为两点之间线段最短!引导语二: 尝试从A点到B点沿圆柱和长方体侧面画出几条路线,你觉得哪条路线最短呢?
你能把A点和B点所在的侧面变成同一平面吗?思考2分钟. 引导语三:将圆柱.长方体侧面剪开展成一个长方形,从A点到B点的最短路线是什么?
你画对了吗? 你画对了吗? 三.?? 巩固练习:
1. 蚂议最短路程问题.
如图所示。有一个圆柱,它的高等于12厘米,底面半径等于3厘米。在圆柱下底面的A点有一只蚂蚁,它想吃到上底面的A点相对的B点处的事物,需要爬行的最短路程是多少?(п的值取3) 答:蚂蚁的最短路程是15厘米 2.有一圆柱形油罐,如图所示,要以A点环绕油罐建旋梯,正好到A点的正上方B点,问旋梯最短要多少米?(己知油罐周长是12米,高AB是5米)[即或: 刚才问题的条件都不变,把问题改成:点B在上底面上且在点A的正上方,蚂蚁从点A出发绕圆柱测面一周到达点B,此时它需要爬行的最短路程又是多少?] 答: 旋梯至少需要13米长. 3. 如图所示,一块砖宽AN=5cm,长ND=10cm,CD上的点B距地面的高BD=8cm.地面上A处的一只蚂蚁到B处吃食,要爬行的最短路线是多少?
?
答:蚂蚁爬行的最短路线是17厘米.四.实际“做一做”: 拿出雕塑底座正面ABCD做纸板模型,
问: 谁有什么办法来检测AD是否垂直于AB? 没有三角板,只有软尺呢? 要每一同学计算并在同桌两人中轮流说明是否垂直的理由. 测量记录: AB=_____ AD=_____ BD=______计算分析:五.?? 挑战“试一试”:
某工厂的大门如图所示,其中四边形ABCD是正方形,上部是以AB为直径的半圆, 其中AD=AB=2米,现有一辆装满货物的卡车,高2.5米,宽1.6米.
问这辆卡车能否通过厂门? 说明理由。 OE=OB=1米 OH=0.8米
答:这辆卡车能够通过厂门.你来总结课堂小结本题课你有什么收获或感想?你还有什么疑问?再见
?
?
先根据题意画出图形,然后解题。回顾思考请同学们拿出昨天做好的圆柱和长方体模型,请同学们想象一下: 有一只小蚂蚁想从A点爬到B点。请大家思考,动手探索:用什么方法可以帮小蚂蚁找到(也就是画出)从A点到B点的最短的路线. 思考、讨论五分钟.探究新知引导语一:如果是一只飞蚂蚁,或鱼缸中的金鱼,则在空间中连接AB. 因为两点之间线段最短!引导语二: 尝试从A点到B点沿圆柱和长方体侧面画出几条路线,你觉得哪条路线最短呢?
你能把A点和B点所在的侧面变成同一平面吗?思考2分钟. 引导语三:将圆柱.长方体侧面剪开展成一个长方形,从A点到B点的最短路线是什么?
你画对了吗? 你画对了吗? 三.?? 巩固练习:
1. 蚂议最短路程问题.
如图所示。有一个圆柱,它的高等于12厘米,底面半径等于3厘米。在圆柱下底面的A点有一只蚂蚁,它想吃到上底面的A点相对的B点处的事物,需要爬行的最短路程是多少?(п的值取3) 答:蚂蚁的最短路程是15厘米 2.有一圆柱形油罐,如图所示,要以A点环绕油罐建旋梯,正好到A点的正上方B点,问旋梯最短要多少米?(己知油罐周长是12米,高AB是5米)[即或: 刚才问题的条件都不变,把问题改成:点B在上底面上且在点A的正上方,蚂蚁从点A出发绕圆柱测面一周到达点B,此时它需要爬行的最短路程又是多少?] 答: 旋梯至少需要13米长. 3. 如图所示,一块砖宽AN=5cm,长ND=10cm,CD上的点B距地面的高BD=8cm.地面上A处的一只蚂蚁到B处吃食,要爬行的最短路线是多少?
?
答:蚂蚁爬行的最短路线是17厘米.四.实际“做一做”: 拿出雕塑底座正面ABCD做纸板模型,
问: 谁有什么办法来检测AD是否垂直于AB? 没有三角板,只有软尺呢? 要每一同学计算并在同桌两人中轮流说明是否垂直的理由. 测量记录: AB=_____ AD=_____ BD=______计算分析:五.?? 挑战“试一试”:
某工厂的大门如图所示,其中四边形ABCD是正方形,上部是以AB为直径的半圆, 其中AD=AB=2米,现有一辆装满货物的卡车,高2.5米,宽1.6米.
问这辆卡车能否通过厂门? 说明理由。 OE=OB=1米 OH=0.8米
答:这辆卡车能够通过厂门.你来总结课堂小结本题课你有什么收获或感想?你还有什么疑问?再见
