人教版八年级数学下册18.2.1矩形课后巩固练习(含答案)
文档属性
| 名称 | 人教版八年级数学下册18.2.1矩形课后巩固练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 313.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-01 16:33:00 | ||
图片预览


文档简介
18.2.1 矩形 课后巩固练习
一、单选题
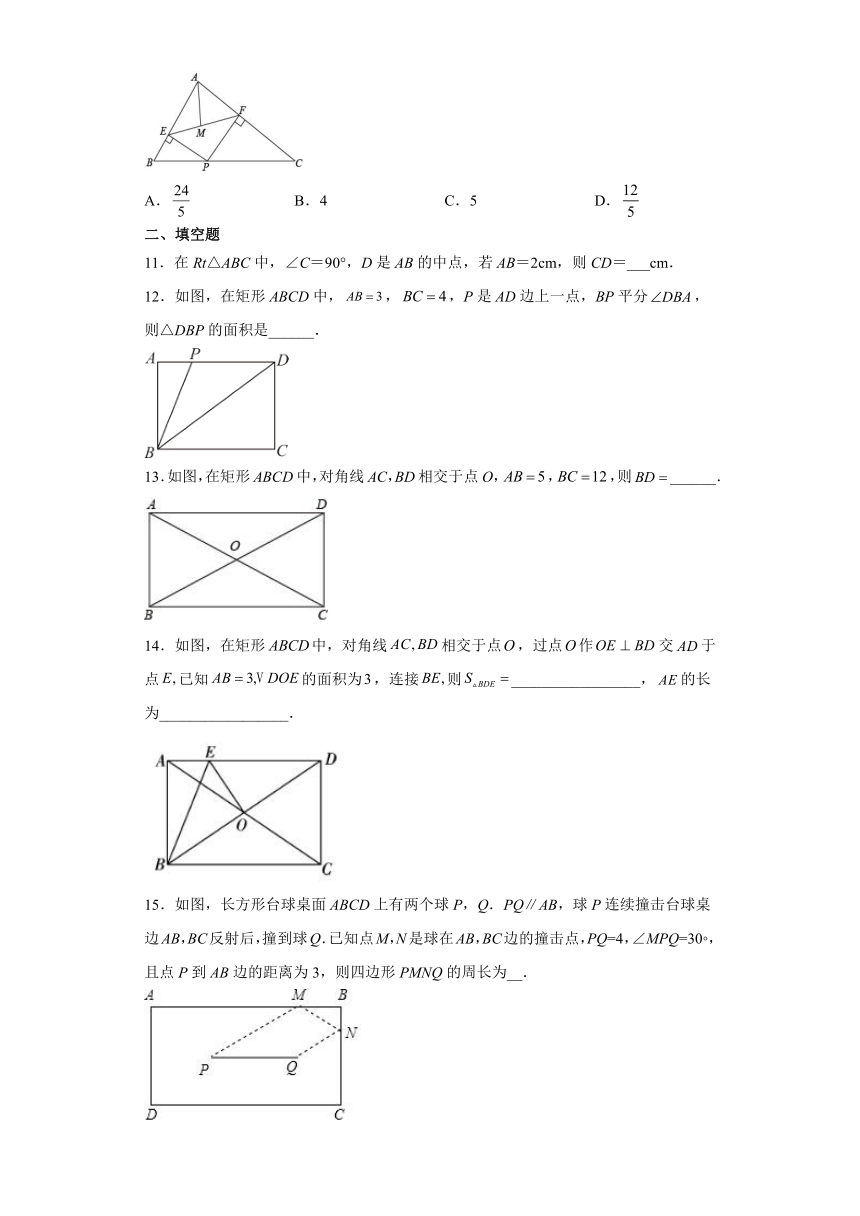
1.在下列图形性质中,矩形不一定具有的是( )
A.对角线互相平分且相等 B.四个角相等
C.既是轴对称图形,又是中心对称图形 D.对角线互相垂直平分
2.如图,在矩形ABCD中,对角线AC、BD相交于点O,交BD于点E,,则的度数为( )
A.40° B.35° C.30° D.25°
3.如图,将矩形纸片ABCD沿AE折叠,使点B落在直角梯形ADCE的中位线FG上,若,则AE的长为( )
A. B.2 C.3 D.
4.直角三角形斜边上的中线长为,则此三角形中平行于斜边的中位线的长为( )
A. B. C. D.无法计算
5.如图,在矩形ABCD中,对角线AC,BD交于点O,点E是OC的中点,点F是BC的中点,若AB=1,BC=,则EF的长是( )
A.2 B.1 C. D.
6.如图,将平行四边形ABCD沿对角线AC折叠,点B的对应点落在点E处,且点B、A、E在同一条直线上,CE交AD于点F,连接ED.下列结论中错误的是( )
A.AF=BC
B.四边形ACDE是矩形
C.图中与△ABC全等的三角形有4个
D.图中有4个等腰三角形
7.如图长方形纸片ABCD,在AD边上取一点E,沿BE折叠,使点C、D分别落在点、处,且点A刚好落在上,若,则∠BED=( )
A.112.5° B.135° C.125° D.100.5°
8.如图,将边长为1的正方形纸片ABCD折叠,使点B的对应点M落在边CD上(不与点C、D重合),折痕为EF,AB的对应线段MG交AD于点N.以下结论正确的有( )①∠MBN=45°;②△MDN的周长是定值;③△MDN的面积是定值.
A.①② B.①③ C.②③ D.①②③
9.如图,在矩形中,,垂足为,,则为( )
A.67.5° B.62.5° C.60° D.22.5°
10.如图,在中,,,,为边上一动点,于,于,为中点,则的最小值为( )
A. B.4 C.5 D.
二、填空题
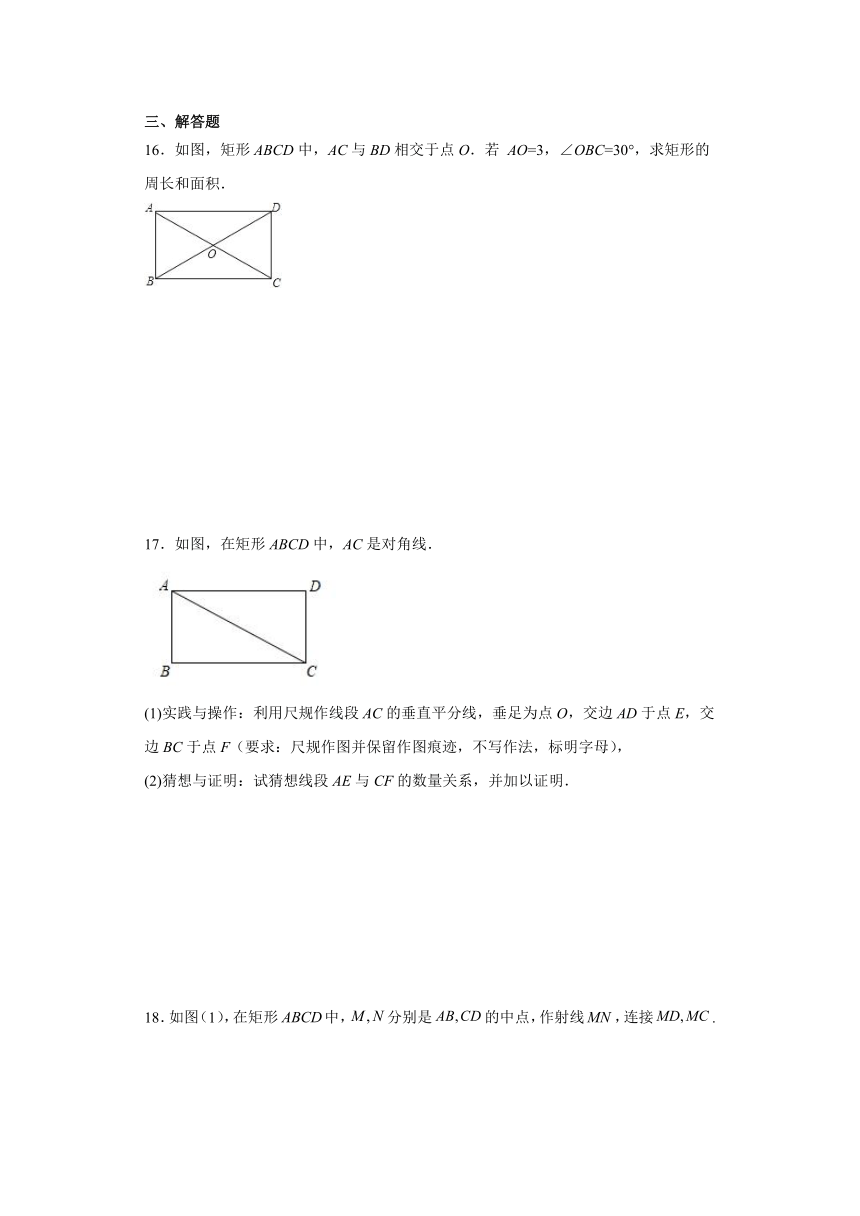
11.在Rt△ABC中,∠C=90°,D是AB的中点,若AB=2cm,则CD=___cm.
12.如图,在矩形ABCD中,,,P是AD边上一点,BP平分,则△DBP的面积是______.
13.如图,在矩形ABCD中,对角线AC,BD相交于点O,,,则______.
14.如图,在矩形中,对角线相交于点,过点作交于点已知的面积为,连接则_________________,的长为_________________.
15.如图,长方形台球桌面ABCD上有两个球P,Q.PQ∥AB,球P连续撞击台球桌边AB,BC反射后,撞到球Q.已知点M,N是球在AB,BC边的撞击点,PQ=4,∠MPQ=30 ,且点P到AB边的距离为3,则四边形PMNQ的周长为__.
三、解答题
16.如图,矩形ABCD中,AC与BD相交于点O.若 AO=3,∠OBC=30°,求矩形的周长和面积.
17.如图,在矩形ABCD中,AC是对角线.
(1)实践与操作:利用尺规作线段AC的垂直平分线,垂足为点O,交边AD于点E,交边BC于点F(要求:尺规作图并保留作图痕迹,不写作法,标明字母),
(2)猜想与证明:试猜想线段AE与CF的数量关系,并加以证明.
18.如图(1),在矩形中,分别是的中点,作射线,连接.
(1)请直接写出线段与的数量关系;
(2)将矩形变为平行四边形,其中为锐角,如图(2),,分别是的中点,过点作交射线于点,交射线于点,连接,求证:;
(3)写出与的数量关系,并证明你的结论.
参考答案
1.D
2.B
3.B
4.B
5.C
6.D
7.A
8.A
9.A
10.D
11.1
12.3.75
13.13
14. 6
15.16.
16.解:∵四边形ABCD是矩形,AO=3,
∴∠ABC=90°,AD=BC,AB=DC,
AO=OC,OB=OD,AC=BD,
∴AC=BD=2AO=6,OB=OC,
∴ABAC=3,
由勾股定理得:BC=3,
∴AB=DC=3,AD=BC=3,
∴矩形ABCD的周长是AB+BC+CD+AD=6+6,
矩形ABCD的面积是AB×BC=3×3.
17.(1)解:如图,
(2)解:.证明如下:
∵四边形ABCD是矩形,
∴.
∴.
∵EF为AC的垂直平分线,
∴.
∴.
∴.
18解:(1)∵四边形ABCD是矩形,
∴AD=BC,∠A=∠B=90°,
∵点M是AB中点,
∴AM=BM,
∴△ADM≌△BCM(SAS),
∴MD=MC;
(2)∵M、N分别是AB、CD的中点,
∴AM=BM,CN=DN,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴DN=AM=CN=BM,
∴四边形ADNM是平行四边形,
∴AD∥MN,
∴,∠AEC=∠NFC=90°,
∴EF=CF,且MF⊥EC,
∴ME=MC;
(3)∠BME=3∠AEM,
证明:∵EM=MC,EF=FC,
∴∠EMF=∠FMC,
∵AB=2BC,M是AB中点,
∴MB=BC,
∴∠BMC=∠BCM,
∵MN∥AD,AD∥BC,
∴AD∥MN∥BC,
∴∠AEM=∠EMF,∠FMC=∠BCM,
∴∠AEM=∠EMF=∠FMC=∠BCM=∠BMC,
∴∠BME=3∠AEM.
一、单选题
1.在下列图形性质中,矩形不一定具有的是( )
A.对角线互相平分且相等 B.四个角相等
C.既是轴对称图形,又是中心对称图形 D.对角线互相垂直平分
2.如图,在矩形ABCD中,对角线AC、BD相交于点O,交BD于点E,,则的度数为( )
A.40° B.35° C.30° D.25°
3.如图,将矩形纸片ABCD沿AE折叠,使点B落在直角梯形ADCE的中位线FG上,若,则AE的长为( )
A. B.2 C.3 D.
4.直角三角形斜边上的中线长为,则此三角形中平行于斜边的中位线的长为( )
A. B. C. D.无法计算
5.如图,在矩形ABCD中,对角线AC,BD交于点O,点E是OC的中点,点F是BC的中点,若AB=1,BC=,则EF的长是( )
A.2 B.1 C. D.
6.如图,将平行四边形ABCD沿对角线AC折叠,点B的对应点落在点E处,且点B、A、E在同一条直线上,CE交AD于点F,连接ED.下列结论中错误的是( )
A.AF=BC
B.四边形ACDE是矩形
C.图中与△ABC全等的三角形有4个
D.图中有4个等腰三角形
7.如图长方形纸片ABCD,在AD边上取一点E,沿BE折叠,使点C、D分别落在点、处,且点A刚好落在上,若,则∠BED=( )
A.112.5° B.135° C.125° D.100.5°
8.如图,将边长为1的正方形纸片ABCD折叠,使点B的对应点M落在边CD上(不与点C、D重合),折痕为EF,AB的对应线段MG交AD于点N.以下结论正确的有( )①∠MBN=45°;②△MDN的周长是定值;③△MDN的面积是定值.
A.①② B.①③ C.②③ D.①②③
9.如图,在矩形中,,垂足为,,则为( )
A.67.5° B.62.5° C.60° D.22.5°
10.如图,在中,,,,为边上一动点,于,于,为中点,则的最小值为( )
A. B.4 C.5 D.
二、填空题
11.在Rt△ABC中,∠C=90°,D是AB的中点,若AB=2cm,则CD=___cm.
12.如图,在矩形ABCD中,,,P是AD边上一点,BP平分,则△DBP的面积是______.
13.如图,在矩形ABCD中,对角线AC,BD相交于点O,,,则______.
14.如图,在矩形中,对角线相交于点,过点作交于点已知的面积为,连接则_________________,的长为_________________.
15.如图,长方形台球桌面ABCD上有两个球P,Q.PQ∥AB,球P连续撞击台球桌边AB,BC反射后,撞到球Q.已知点M,N是球在AB,BC边的撞击点,PQ=4,∠MPQ=30 ,且点P到AB边的距离为3,则四边形PMNQ的周长为__.
三、解答题
16.如图,矩形ABCD中,AC与BD相交于点O.若 AO=3,∠OBC=30°,求矩形的周长和面积.
17.如图,在矩形ABCD中,AC是对角线.
(1)实践与操作:利用尺规作线段AC的垂直平分线,垂足为点O,交边AD于点E,交边BC于点F(要求:尺规作图并保留作图痕迹,不写作法,标明字母),
(2)猜想与证明:试猜想线段AE与CF的数量关系,并加以证明.
18.如图(1),在矩形中,分别是的中点,作射线,连接.
(1)请直接写出线段与的数量关系;
(2)将矩形变为平行四边形,其中为锐角,如图(2),,分别是的中点,过点作交射线于点,交射线于点,连接,求证:;
(3)写出与的数量关系,并证明你的结论.
参考答案
1.D
2.B
3.B
4.B
5.C
6.D
7.A
8.A
9.A
10.D
11.1
12.3.75
13.13
14. 6
15.16.
16.解:∵四边形ABCD是矩形,AO=3,
∴∠ABC=90°,AD=BC,AB=DC,
AO=OC,OB=OD,AC=BD,
∴AC=BD=2AO=6,OB=OC,
∴ABAC=3,
由勾股定理得:BC=3,
∴AB=DC=3,AD=BC=3,
∴矩形ABCD的周长是AB+BC+CD+AD=6+6,
矩形ABCD的面积是AB×BC=3×3.
17.(1)解:如图,
(2)解:.证明如下:
∵四边形ABCD是矩形,
∴.
∴.
∵EF为AC的垂直平分线,
∴.
∴.
∴.
18解:(1)∵四边形ABCD是矩形,
∴AD=BC,∠A=∠B=90°,
∵点M是AB中点,
∴AM=BM,
∴△ADM≌△BCM(SAS),
∴MD=MC;
(2)∵M、N分别是AB、CD的中点,
∴AM=BM,CN=DN,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴DN=AM=CN=BM,
∴四边形ADNM是平行四边形,
∴AD∥MN,
∴,∠AEC=∠NFC=90°,
∴EF=CF,且MF⊥EC,
∴ME=MC;
(3)∠BME=3∠AEM,
证明:∵EM=MC,EF=FC,
∴∠EMF=∠FMC,
∵AB=2BC,M是AB中点,
∴MB=BC,
∴∠BMC=∠BCM,
∵MN∥AD,AD∥BC,
∴AD∥MN∥BC,
∴∠AEM=∠EMF,∠FMC=∠BCM,
∴∠AEM=∠EMF=∠FMC=∠BCM=∠BMC,
∴∠BME=3∠AEM.
