人教版(五四制)九年级数学上册 第二十八章二次函数单元测试(含解析)
文档属性
| 名称 | 人教版(五四制)九年级数学上册 第二十八章二次函数单元测试(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 569.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-01 17:23:04 | ||
图片预览


文档简介
人教版九年级上册二次函数单元测试
(共21题)
一、选择题(共10题,共20分)
抛物线 的顶点坐标是
A. B. C. D.
若关于 的函数 是二次函数,则 的取值范围是
A. B. C. D.
将抛物线 向上平移 个单位长度,再向右平移 个单位长度,所得到的抛物线为
A. B.
C. D.
抛物线 与 轴有两个不同的交点,则一元二次方程 的根的情况是
A.有两个不同的实数根 B.有两个相同的实数根
C.没有实数根 D.无法判定
抛物线的对称轴为直线 , 的最大值为 ,且与 的图象开口大小相同.则这条抛物线解析式为
A. B.
C. D.
已知二次函数的图象经过 ,顶点为 ,将该图象向右平移,当它再次经过点 时,所得抛物线的函数表达式为
A. B.
C. D.
根据下表列出的函数 的几组 与 的对应值,判断方程 一个解 的范围是
A. B.
C. D.
在同一坐标系中,作 ,, 的图象,则它们
A.都是关于 轴对称 B.顶点都在原点
C.都是抛物线开口向上 D.以上都不对
二次函数 的图象如何平移可得到 的图象
A.向左平移 个单位,向上平移 个单位
B.向右平移 个单位,向上平移 个单位
C.向左平移 个单位,向下平移 个单位
D.向右平移 个单位,向下平移 个单位
二次函数 的图象如图所示,那么一次函数 的图象大致是
A. B. C. D.
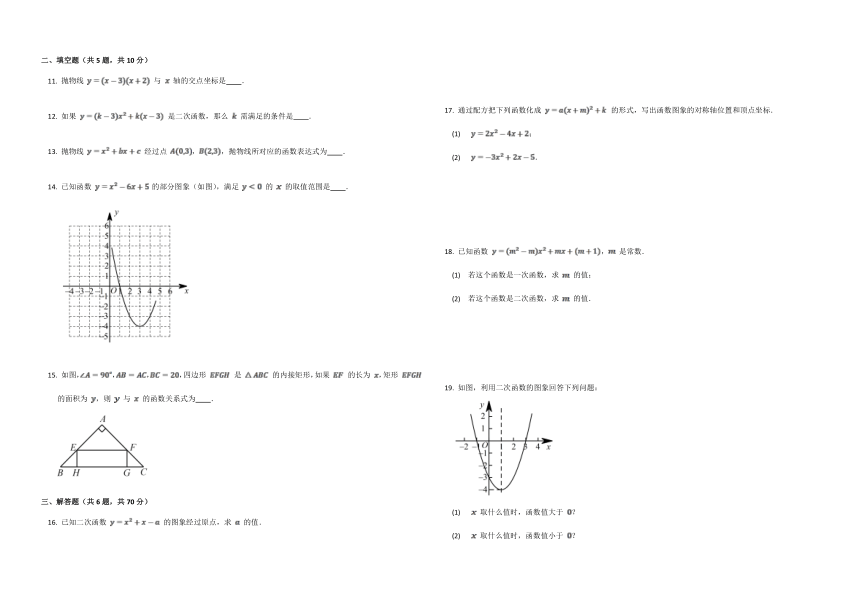
二、填空题(共5题,共10分)
抛物线 与 轴的交点坐标是 .
如果 是二次函数,那么 需满足的条件是 .
抛物线 经过点 ,,抛物线所对应的函数表达式为 .
已知函数 的部分图象(如图),满足 的 的取值范围是 .
如图,,,,四边形 是 的内接矩形,如果 的长为 ,矩形 的面积为 ,则 与 的函数关系式为 .
三、解答题(共6题,共70分)
已知二次函数 的图象经过原点,求 的值.
通过配方把下列函数化成 的形式,写出函数图象的对称轴位置和顶点坐标.
(1) ;
(2) .
已知函数 , 是常数.
(1) 若这个函数是一次函数,求 的值;
(2) 若这个函数是二次函数,求 的值.
如图,利用二次函数的图象回答下列问题:
(1) 取什么值时,函数值大于 ?
(2) 取什么值时,函数值小于 ?
(3) 二次函数的最小值是多少?
(4) 函数值随 的增大是怎样变化的?
点 , 在二次函数 的图象上,求 , 的值.
宏兴企业接到一批产品的生产任务,按要求必须在 天内完成.已知每件产品的出厂价为 元.工人甲第 天生产的产品数量为 件, 与 满足如下关系:.
(1) 工人甲第几天生产的产品数量为 件?
(2) 设第 天生产的产品成本为 元/ 件, 与 的函数图象如图.工人甲第 天创造的利润为 元,求 与 的函数关系式,并求出第几天时,利润最大,最大利润是多少?
答案
一、选择题(共10题)
1. 【答案】A
【知识点】y=a(x-h)^2+k的图象
2. 【答案】B
【解析】 函数 是二次函数,
,即 .
【知识点】二次函数的概念
3. 【答案】B
【知识点】二次函数的图象变换
4. 【答案】A
【知识点】二次函数与方程
5. 【答案】B
【知识点】二次函数的解析式
6. 【答案】C
【知识点】二次函数的图象变换、二次函数的解析式
7. 【答案】C
【知识点】二次函数与方程
8. 【答案】A
【知识点】y=ax^2的图象
9. 【答案】C
【解析】二次函数 的顶点坐标为 , 的顶点坐标为 ,
只需将函数 的图象向左移动 个单位,向下移动 个单位即可.
故选:C.
【知识点】二次函数的图象变换
10. 【答案】C
【解析】 二次函数图象开口向上,
,
对称轴为直线 ,
,
一次函数 的图象经过二、一、四象限.
【知识点】二次函数图象与系数的关系
二、填空题(共5题)
11. 【答案】 ,
【知识点】二次函数与方程
12. 【答案】
【解析】 是二次函数,
,解得 ,
需满足的条件是 .
【知识点】二次函数的概念
13. 【答案】略
【知识点】二次函数的解析式
14. 【答案】
【知识点】二次函数与不等式
15. 【答案】
【解析】 ,,
.
四边形 是 的内接矩形,
,,,
,
.
,,
,
.
【知识点】二次函数的应用
三、解答题(共6题)
16. 【答案】 抛物线 过 ,
.
.
【知识点】y=ax^2+bx+c的图象
17. 【答案】
(1) ,对称轴是过点 且平行于 轴的直线,顶点坐标是 .
(2) ,对称轴是过点 且平行于 轴的直线,顶点坐标是 .
【知识点】二次函数的三种形式之间转化
18. 【答案】
(1) 由题意可知
解得 .
(2) 由题意可知 ,
解得 且 .
【知识点】二次函数的概念、一次函数的概念
19. 【答案】
(1) 或 .
(2) .
(3) .
(4) 当 时,函数值随 的增大而减小,
当 时,函数值随 的增大而增大.
【知识点】二次函数与不等式、二次函数的增减性、二次函数的最值
20. 【答案】 在抛物线 上,
.
在抛物线 上,
,
.
【知识点】二次函数的解析式
21. 【答案】
(1) 根据题意,得:
若 .得:.不符合题意;
.
解得:.
答:工人甲第 天生产的产品数量为 件.
(2) 由函数图象知,当 时,,当 时,设 ,
将 , 代入,得:
解得:
;
①当 时,,
随 的增大而增大,
当 时, 元;
②当 时,
当 时,,
,
当 时, 取得最大值,最大值为 元,
答:第 天时,利润最大,最大利润是 元.
【知识点】一次函数的应用、二次函数的应用、y=ax^2+bx+c的图象
(共21题)
一、选择题(共10题,共20分)
抛物线 的顶点坐标是
A. B. C. D.
若关于 的函数 是二次函数,则 的取值范围是
A. B. C. D.
将抛物线 向上平移 个单位长度,再向右平移 个单位长度,所得到的抛物线为
A. B.
C. D.
抛物线 与 轴有两个不同的交点,则一元二次方程 的根的情况是
A.有两个不同的实数根 B.有两个相同的实数根
C.没有实数根 D.无法判定
抛物线的对称轴为直线 , 的最大值为 ,且与 的图象开口大小相同.则这条抛物线解析式为
A. B.
C. D.
已知二次函数的图象经过 ,顶点为 ,将该图象向右平移,当它再次经过点 时,所得抛物线的函数表达式为
A. B.
C. D.
根据下表列出的函数 的几组 与 的对应值,判断方程 一个解 的范围是
A. B.
C. D.
在同一坐标系中,作 ,, 的图象,则它们
A.都是关于 轴对称 B.顶点都在原点
C.都是抛物线开口向上 D.以上都不对
二次函数 的图象如何平移可得到 的图象
A.向左平移 个单位,向上平移 个单位
B.向右平移 个单位,向上平移 个单位
C.向左平移 个单位,向下平移 个单位
D.向右平移 个单位,向下平移 个单位
二次函数 的图象如图所示,那么一次函数 的图象大致是
A. B. C. D.
二、填空题(共5题,共10分)
抛物线 与 轴的交点坐标是 .
如果 是二次函数,那么 需满足的条件是 .
抛物线 经过点 ,,抛物线所对应的函数表达式为 .
已知函数 的部分图象(如图),满足 的 的取值范围是 .
如图,,,,四边形 是 的内接矩形,如果 的长为 ,矩形 的面积为 ,则 与 的函数关系式为 .
三、解答题(共6题,共70分)
已知二次函数 的图象经过原点,求 的值.
通过配方把下列函数化成 的形式,写出函数图象的对称轴位置和顶点坐标.
(1) ;
(2) .
已知函数 , 是常数.
(1) 若这个函数是一次函数,求 的值;
(2) 若这个函数是二次函数,求 的值.
如图,利用二次函数的图象回答下列问题:
(1) 取什么值时,函数值大于 ?
(2) 取什么值时,函数值小于 ?
(3) 二次函数的最小值是多少?
(4) 函数值随 的增大是怎样变化的?
点 , 在二次函数 的图象上,求 , 的值.
宏兴企业接到一批产品的生产任务,按要求必须在 天内完成.已知每件产品的出厂价为 元.工人甲第 天生产的产品数量为 件, 与 满足如下关系:.
(1) 工人甲第几天生产的产品数量为 件?
(2) 设第 天生产的产品成本为 元/ 件, 与 的函数图象如图.工人甲第 天创造的利润为 元,求 与 的函数关系式,并求出第几天时,利润最大,最大利润是多少?
答案
一、选择题(共10题)
1. 【答案】A
【知识点】y=a(x-h)^2+k的图象
2. 【答案】B
【解析】 函数 是二次函数,
,即 .
【知识点】二次函数的概念
3. 【答案】B
【知识点】二次函数的图象变换
4. 【答案】A
【知识点】二次函数与方程
5. 【答案】B
【知识点】二次函数的解析式
6. 【答案】C
【知识点】二次函数的图象变换、二次函数的解析式
7. 【答案】C
【知识点】二次函数与方程
8. 【答案】A
【知识点】y=ax^2的图象
9. 【答案】C
【解析】二次函数 的顶点坐标为 , 的顶点坐标为 ,
只需将函数 的图象向左移动 个单位,向下移动 个单位即可.
故选:C.
【知识点】二次函数的图象变换
10. 【答案】C
【解析】 二次函数图象开口向上,
,
对称轴为直线 ,
,
一次函数 的图象经过二、一、四象限.
【知识点】二次函数图象与系数的关系
二、填空题(共5题)
11. 【答案】 ,
【知识点】二次函数与方程
12. 【答案】
【解析】 是二次函数,
,解得 ,
需满足的条件是 .
【知识点】二次函数的概念
13. 【答案】略
【知识点】二次函数的解析式
14. 【答案】
【知识点】二次函数与不等式
15. 【答案】
【解析】 ,,
.
四边形 是 的内接矩形,
,,,
,
.
,,
,
.
【知识点】二次函数的应用
三、解答题(共6题)
16. 【答案】 抛物线 过 ,
.
.
【知识点】y=ax^2+bx+c的图象
17. 【答案】
(1) ,对称轴是过点 且平行于 轴的直线,顶点坐标是 .
(2) ,对称轴是过点 且平行于 轴的直线,顶点坐标是 .
【知识点】二次函数的三种形式之间转化
18. 【答案】
(1) 由题意可知
解得 .
(2) 由题意可知 ,
解得 且 .
【知识点】二次函数的概念、一次函数的概念
19. 【答案】
(1) 或 .
(2) .
(3) .
(4) 当 时,函数值随 的增大而减小,
当 时,函数值随 的增大而增大.
【知识点】二次函数与不等式、二次函数的增减性、二次函数的最值
20. 【答案】 在抛物线 上,
.
在抛物线 上,
,
.
【知识点】二次函数的解析式
21. 【答案】
(1) 根据题意,得:
若 .得:.不符合题意;
.
解得:.
答:工人甲第 天生产的产品数量为 件.
(2) 由函数图象知,当 时,,当 时,设 ,
将 , 代入,得:
解得:
;
①当 时,,
随 的增大而增大,
当 时, 元;
②当 时,
当 时,,
,
当 时, 取得最大值,最大值为 元,
答:第 天时,利润最大,最大利润是 元.
【知识点】一次函数的应用、二次函数的应用、y=ax^2+bx+c的图象
