人教版八年级下册 18.2.2菱形同步训练(含答案)
文档属性
| 名称 | 人教版八年级下册 18.2.2菱形同步训练(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 471.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-01 21:55:32 | ||
图片预览

文档简介
18.2.2 菱形 同步训练
一、单选题
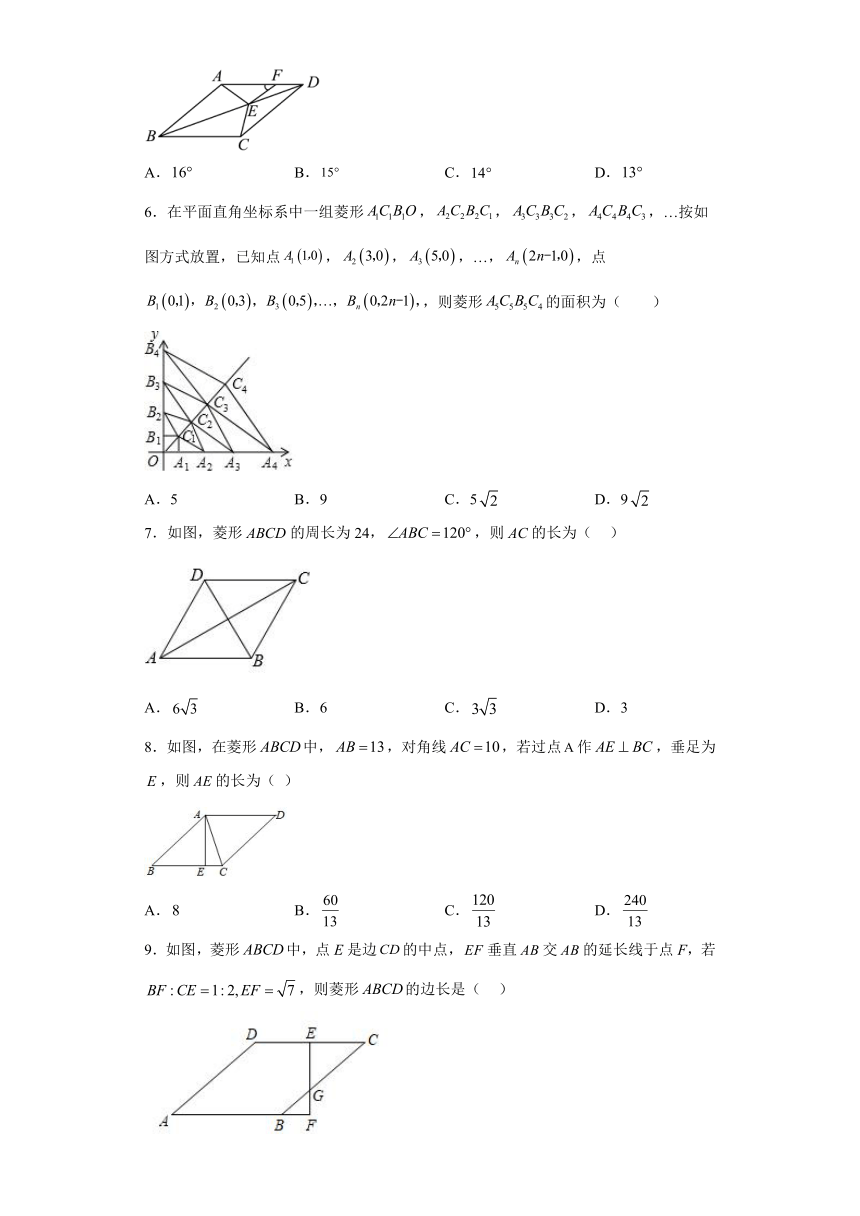
1.如图,在菱形ABCD中,∠A=60°,AD=4,点P是AB边上的一个动点,点E、F分别是DP、BP的中点,则线段EF的长为( )
A.2 B.4 C. D.
2.已知菱形的两条对角线,则菱形的面积为( )
A.48 B.40 C.24 D.20
3.如图,在菱形中,,对角线、相交于点O,E为中点,则的度数为( )
A.70° B.65° C.55° D.35°
4.如图,在平行四边形ABCD,尺规作图:以点A为圆心,AB的长为半径画弧交AD于点F,分别以点B,F为圆心,以大于 BF的长为半径画弧交于点G,做射线AG交BC与点E,若BF=12,AB=10,则AE的长为( ).
A.17 B.16 C.15 D.14
5.如图,在菱形中,,点为对角线上一点,为边上一点,连接、、,若,,则的度数为( )
A. B. C. D.
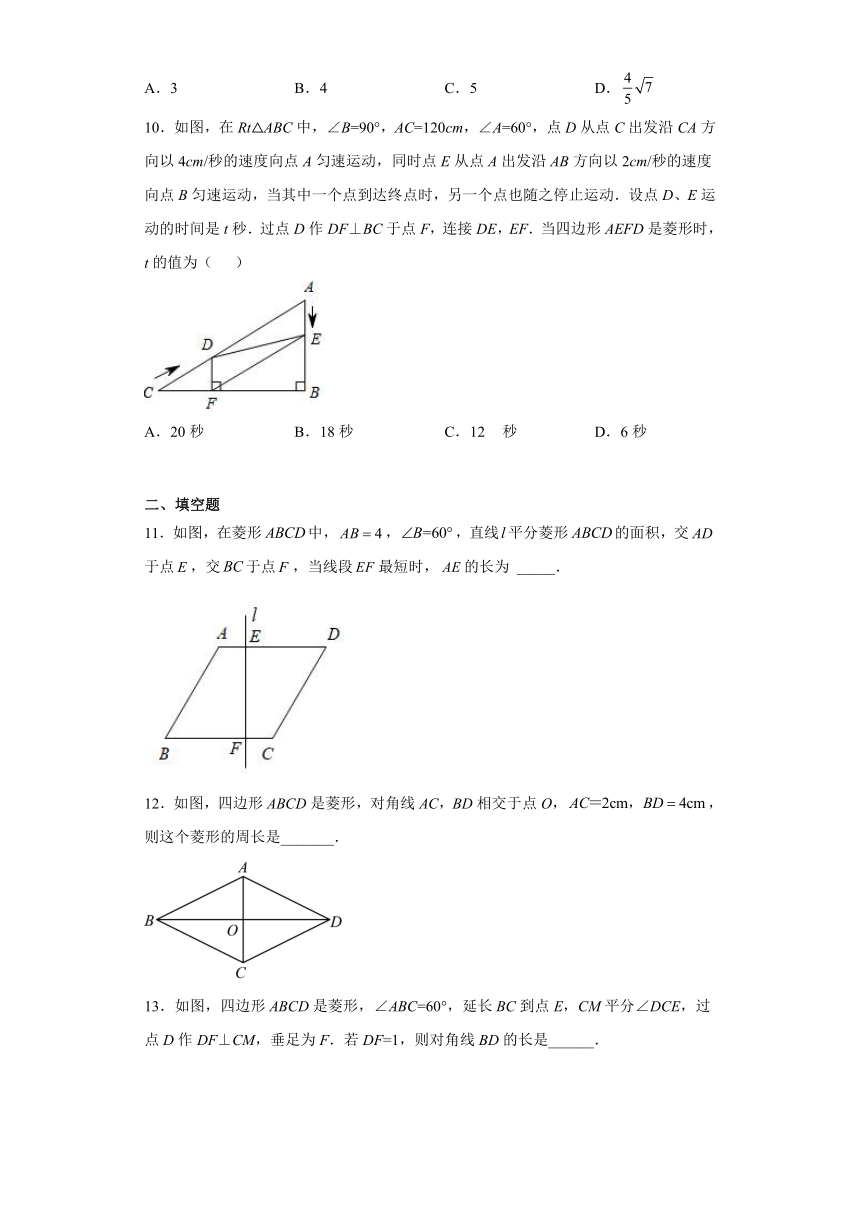
6.在平面直角坐标系中一组菱形,,,,…按如图方式放置,已知点,,,…,,点,则菱形的面积为( )
A.5 B.9 C.5 D.9
7.如图,菱形ABCD的周长为24,,则AC的长为( )
A. B.6 C. D.3
8.如图,在菱形中,,对角线,若过点作,垂足为,则的长为( )
A. B. C. D.
9.如图,菱形中,点E是边的中点,垂直交的延长线于点F,若,则菱形的边长是( )
A.3 B.4 C.5 D.
10.如图,在Rt△ABC中,∠B=90°,AC=120cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒.过点D作DF⊥BC于点F,连接DE,EF.当四边形AEFD是菱形时,t的值为( )
A.20秒 B.18秒 C.12 秒 D.6秒
二、填空题
11.如图,在菱形中,,,直线平分菱形的面积,交于点,交于点,当线段最短时,的长为 _____.
12.如图,四边形ABCD是菱形,对角线AC,BD相交于点O,,则这个菱形的周长是_______.
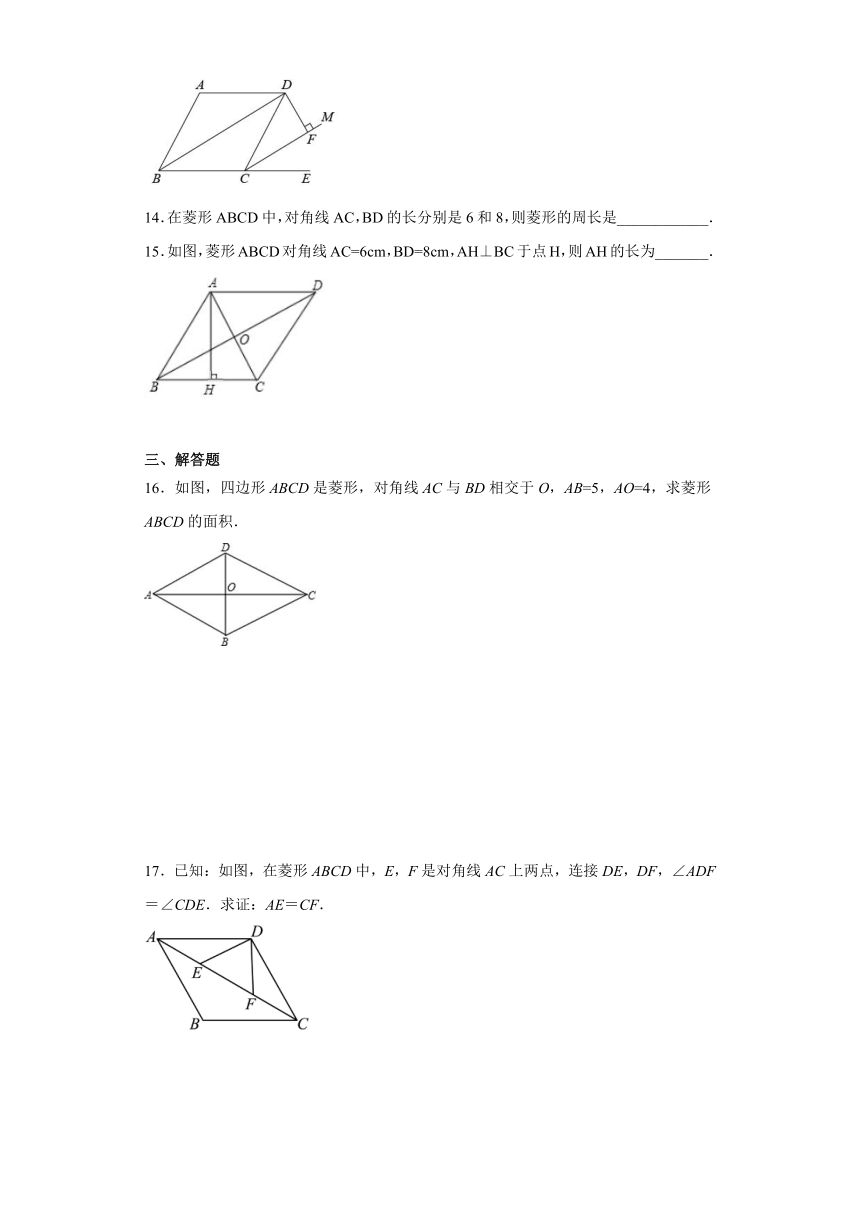
13.如图,四边形ABCD是菱形,∠ABC=60°,延长BC到点E,CM平分∠DCE,过点D作DF⊥CM,垂足为F.若DF=1,则对角线BD的长是______.
14.在菱形ABCD中,对角线AC,BD的长分别是6和8,则菱形的周长是____________.
15.如图,菱形ABCD对角线AC=6cm,BD=8cm,AH⊥BC于点H,则AH的长为_______.
三、解答题
16.如图,四边形ABCD是菱形,对角线AC与BD相交于O,AB=5,AO=4,求菱形ABCD的面积.
17.已知:如图,在菱形ABCD中,E,F是对角线AC上两点,连接DE,DF,∠ADF=∠CDE.求证:AE=CF.
18.如图,在菱形ABDC中,点E,F分别在边CD,BD上,.求证:.
19.如图:在中,,、、分别是、、边上的中点.
求证:四边形是菱形.
20.如图,在菱形ABCD中,对角线AC、BD相交于点O,点E是AD的中点,连接OE,过点D作DF∥AC交OE的延长线于点F,连接AF.
(1)求证:≌;
(2)判定四边形AODF的形状并说明理由.
参考答案
1.A
2.C
3.C
4.B
5.A
6.B
7.A
8.C
9.B
10.A
11.
12.cm
13.
14.20.
15.cm
16.∵四边形ABCD是菱形,对角线AC与BD相交于O,
∴AC⊥BD,BD=2BO,AC=2AO=2×4=8,
∵AB=5,AO=4,
∴BO==3,
∴BD=2BO=2×3=6,
∴S菱形ABCD==24.
17.解:∵四边形是菱形,E,F是对角线AC上两点,
∴,.
∵,
∴,
即.
在和中,,
∴,
∴.
18.证明:四边形是菱形,
,
在和中,
,
,
.
19. 、、分别是、、边上的中点,
,EFBC,DE=AB,DEAB,
∴四边形是平行四边形,
又 ,
EF=DE,
四边形BDEF是菱形.
20.(1)证明:∵E是AD的中点,
∴AE=DE,
∵DF∥AC,
∴∠OAD=∠ADF,
∵∠AEO=∠DEF,
∴△AOE≌△DFE(ASA);
(2)解:四边形AODF为矩形.
理由:∵△AOE≌△DFE,
∴AO=DF,
∵DF∥AC,
∴四边形AODF为平行四边形,
∵四边形ABCD为菱形,
∴AC⊥BD,
即∠AOD=90°,
∴平行四边形AODF为矩形.
一、单选题
1.如图,在菱形ABCD中,∠A=60°,AD=4,点P是AB边上的一个动点,点E、F分别是DP、BP的中点,则线段EF的长为( )
A.2 B.4 C. D.
2.已知菱形的两条对角线,则菱形的面积为( )
A.48 B.40 C.24 D.20
3.如图,在菱形中,,对角线、相交于点O,E为中点,则的度数为( )
A.70° B.65° C.55° D.35°
4.如图,在平行四边形ABCD,尺规作图:以点A为圆心,AB的长为半径画弧交AD于点F,分别以点B,F为圆心,以大于 BF的长为半径画弧交于点G,做射线AG交BC与点E,若BF=12,AB=10,则AE的长为( ).
A.17 B.16 C.15 D.14
5.如图,在菱形中,,点为对角线上一点,为边上一点,连接、、,若,,则的度数为( )
A. B. C. D.
6.在平面直角坐标系中一组菱形,,,,…按如图方式放置,已知点,,,…,,点,则菱形的面积为( )
A.5 B.9 C.5 D.9
7.如图,菱形ABCD的周长为24,,则AC的长为( )
A. B.6 C. D.3
8.如图,在菱形中,,对角线,若过点作,垂足为,则的长为( )
A. B. C. D.
9.如图,菱形中,点E是边的中点,垂直交的延长线于点F,若,则菱形的边长是( )
A.3 B.4 C.5 D.
10.如图,在Rt△ABC中,∠B=90°,AC=120cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒.过点D作DF⊥BC于点F,连接DE,EF.当四边形AEFD是菱形时,t的值为( )
A.20秒 B.18秒 C.12 秒 D.6秒
二、填空题
11.如图,在菱形中,,,直线平分菱形的面积,交于点,交于点,当线段最短时,的长为 _____.
12.如图,四边形ABCD是菱形,对角线AC,BD相交于点O,,则这个菱形的周长是_______.
13.如图,四边形ABCD是菱形,∠ABC=60°,延长BC到点E,CM平分∠DCE,过点D作DF⊥CM,垂足为F.若DF=1,则对角线BD的长是______.
14.在菱形ABCD中,对角线AC,BD的长分别是6和8,则菱形的周长是____________.
15.如图,菱形ABCD对角线AC=6cm,BD=8cm,AH⊥BC于点H,则AH的长为_______.
三、解答题
16.如图,四边形ABCD是菱形,对角线AC与BD相交于O,AB=5,AO=4,求菱形ABCD的面积.
17.已知:如图,在菱形ABCD中,E,F是对角线AC上两点,连接DE,DF,∠ADF=∠CDE.求证:AE=CF.
18.如图,在菱形ABDC中,点E,F分别在边CD,BD上,.求证:.
19.如图:在中,,、、分别是、、边上的中点.
求证:四边形是菱形.
20.如图,在菱形ABCD中,对角线AC、BD相交于点O,点E是AD的中点,连接OE,过点D作DF∥AC交OE的延长线于点F,连接AF.
(1)求证:≌;
(2)判定四边形AODF的形状并说明理由.
参考答案
1.A
2.C
3.C
4.B
5.A
6.B
7.A
8.C
9.B
10.A
11.
12.cm
13.
14.20.
15.cm
16.∵四边形ABCD是菱形,对角线AC与BD相交于O,
∴AC⊥BD,BD=2BO,AC=2AO=2×4=8,
∵AB=5,AO=4,
∴BO==3,
∴BD=2BO=2×3=6,
∴S菱形ABCD==24.
17.解:∵四边形是菱形,E,F是对角线AC上两点,
∴,.
∵,
∴,
即.
在和中,,
∴,
∴.
18.证明:四边形是菱形,
,
在和中,
,
,
.
19. 、、分别是、、边上的中点,
,EFBC,DE=AB,DEAB,
∴四边形是平行四边形,
又 ,
EF=DE,
四边形BDEF是菱形.
20.(1)证明:∵E是AD的中点,
∴AE=DE,
∵DF∥AC,
∴∠OAD=∠ADF,
∵∠AEO=∠DEF,
∴△AOE≌△DFE(ASA);
(2)解:四边形AODF为矩形.
理由:∵△AOE≌△DFE,
∴AO=DF,
∵DF∥AC,
∴四边形AODF为平行四边形,
∵四边形ABCD为菱形,
∴AC⊥BD,
即∠AOD=90°,
∴平行四边形AODF为矩形.
