10.1.1 生活中的轴对称 教案
图片预览
文档简介
中小学教育资源及组卷应用平台
10.1.1 生活中的轴对称 教学设计
课题 10.1.1 生活中的轴对称 单元 第9 单元 学科 数学 年级 七年级(下)
教材分析 通过观察、分析现实生活实例和典型图形的过程,认识轴对称和轴对称图形,会找出简单的轴对称图形的对称轴,了解轴对称和轴对称图形的联系和区别.
核心素养分析 通过观察、分析现实生活中轴对称的过程。发展观察能力、思维能力、操作能力、归纳能力.
学习目标 1.通过生活中的具体实例认识轴对称,能说出轴对称图形和关于直线成轴对称这两个概念.2.能识别简单的轴对称图形,画出其对称轴,找到对称点.
重点 正确理解轴对称图形以及轴对称的概念.
难点 能正确区分轴对称图形和轴对称.
教学过程
教学环节 教师活动 学生活动 设计意图
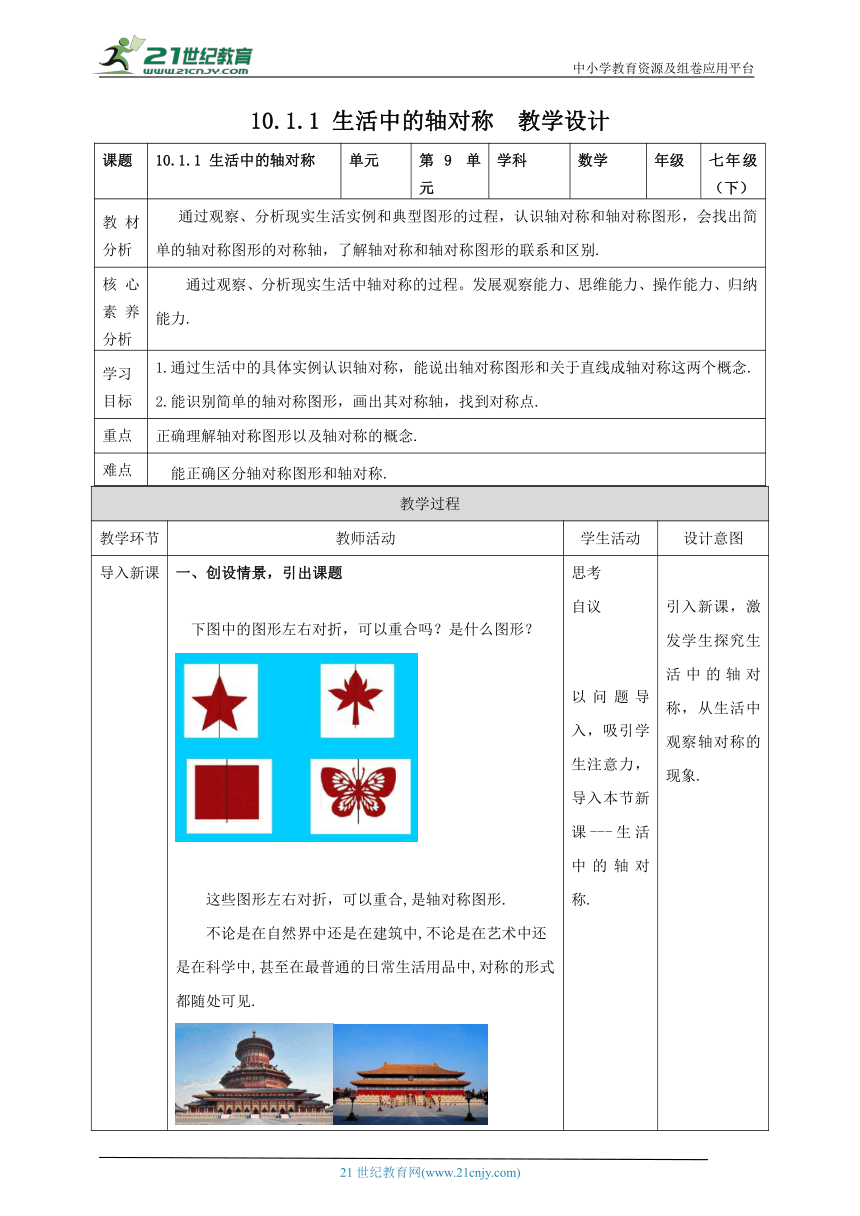
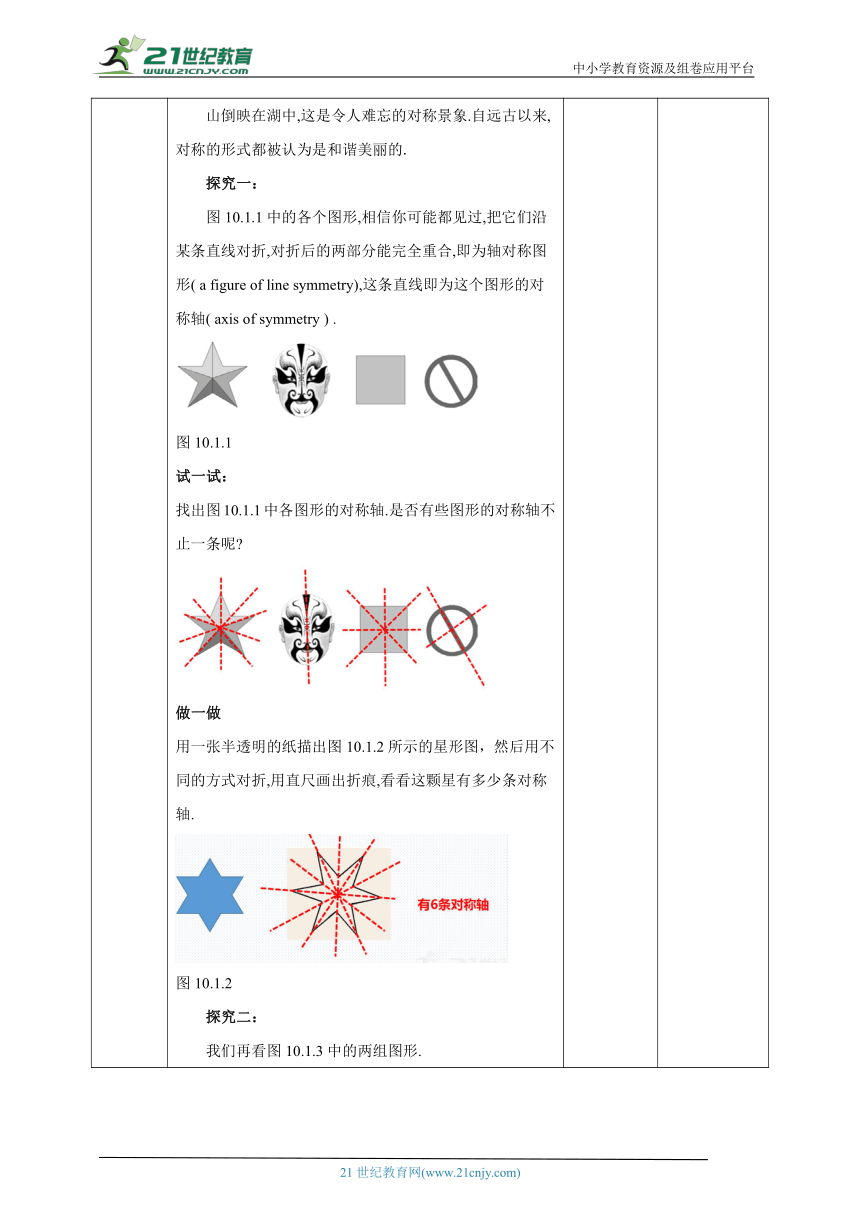
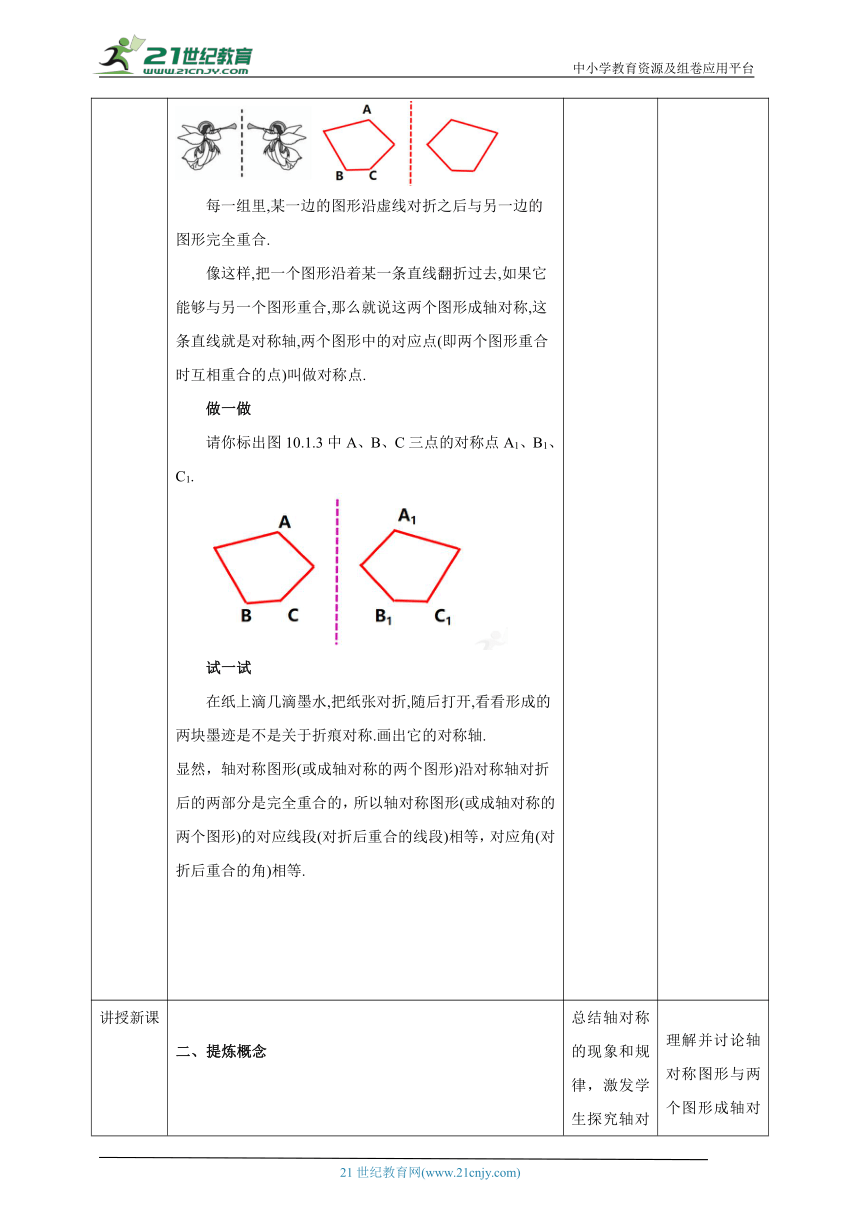
导入新课 一、创设情景,引出课题 下图中的图形左右对折,可以重合吗?是什么图形?这些图形左右对折,可以重合,是轴对称图形.不论是在自然界中还是在建筑中,不论是在艺术中还是在科学中,甚至在最普通的日常生活用品中,对称的形式都随处可见.山倒映在湖中,这是令人难忘的对称景象.自远古以来,对称的形式都被认为是和谐美丽的.探究一:图10.1.1中的各个图形,相信你可能都见过,把它们沿某条直线对折,对折后的两部分能完全重合,即为轴对称图形( a figure of line symmetry),这条直线即为这个图形的对称轴( axis of symmetry ) .图10.1.1试一试:找出图10.1.1中各图形的对称轴.是否有些图形的对称轴不止一条呢 做一做用一张半透明的纸描出图10.1.2所示的星形图,然后用不同的方式对折,用直尺画出折痕,看看这颗星有多少条对称轴.图10.1.2探究二:我们再看图10.1.3中的两组图形.每一组里,某一边的图形沿虚线对折之后与另一边的图形完全重合.像这样,把一个图形沿着某一条直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形成轴对称,这条直线就是对称轴,两个图形中的对应点(即两个图形重合时互相重合的点)叫做对称点.做一做请你标出图10.1.3中A、B、C三点的对称点A1、B1、C1.试一试在纸上滴几滴墨水,把纸张对折,随后打开,看看形成的两块墨迹是不是关于折痕对称.画出它的对称轴.显然,轴对称图形(或成轴对称的两个图形)沿对称轴对折后的两部分是完全重合的,所以轴对称图形(或成轴对称的两个图形)的对应线段(对折后重合的线段)相等,对应角(对折后重合的角)相等. 思考自议以问题导入,吸引学生注意力,导入本节新课---生活中的轴对称. 引入新课,激发学生探究生活中的轴对称,从生活中观察轴对称的现象.
讲授新课 二、提炼概念三、典例精讲例:下面这些图形是轴对称图形吗?是,是,否 总结轴对称的现象和规律,激发学生探究轴对称的求知欲. 理解并讨论轴对称图形与两个图形成轴对称的区别和联系.
课堂练习 四、巩固训练1.甲骨文是我国的一种古代文字,下面是“北”“比”“鼎”“射”四个字的甲骨文,其中不是轴对称图形的是( )B2. 如图所示的图形中,左边图形与右边图形成轴对称的是( )D3.如图,直线MN是四边形AMBN的对称 轴,点P是直线MN上的点,下列判断错误的是( ) A.AM=BM B.AP=BN C.∠MAP=∠MBP D.∠ANM=∠BNMB4. 如图,AC=7,∠C=60°,△ABC与△A′B′C′关于直线l对称,则∠C′=________,A′C′=________.60° ,7 5.如下图,△ABC与△DEF关于直线 l轴对称,点P、Q、R分别是线段AD、BE、CF与直线l的交点.(1)如果AP=2cm,BQ=5cm ,你能说出DP、EQ的长吗?(2)如果线段AB=7cm,AC=5cm,你能说出DE、DF的长吗? 为什么?(3)由此,可以得出什么结论?
课堂小结 课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
10.1.1 生活中的轴对称 教学设计
课题 10.1.1 生活中的轴对称 单元 第9 单元 学科 数学 年级 七年级(下)
教材分析 通过观察、分析现实生活实例和典型图形的过程,认识轴对称和轴对称图形,会找出简单的轴对称图形的对称轴,了解轴对称和轴对称图形的联系和区别.
核心素养分析 通过观察、分析现实生活中轴对称的过程。发展观察能力、思维能力、操作能力、归纳能力.
学习目标 1.通过生活中的具体实例认识轴对称,能说出轴对称图形和关于直线成轴对称这两个概念.2.能识别简单的轴对称图形,画出其对称轴,找到对称点.
重点 正确理解轴对称图形以及轴对称的概念.
难点 能正确区分轴对称图形和轴对称.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 一、创设情景,引出课题 下图中的图形左右对折,可以重合吗?是什么图形?这些图形左右对折,可以重合,是轴对称图形.不论是在自然界中还是在建筑中,不论是在艺术中还是在科学中,甚至在最普通的日常生活用品中,对称的形式都随处可见.山倒映在湖中,这是令人难忘的对称景象.自远古以来,对称的形式都被认为是和谐美丽的.探究一:图10.1.1中的各个图形,相信你可能都见过,把它们沿某条直线对折,对折后的两部分能完全重合,即为轴对称图形( a figure of line symmetry),这条直线即为这个图形的对称轴( axis of symmetry ) .图10.1.1试一试:找出图10.1.1中各图形的对称轴.是否有些图形的对称轴不止一条呢 做一做用一张半透明的纸描出图10.1.2所示的星形图,然后用不同的方式对折,用直尺画出折痕,看看这颗星有多少条对称轴.图10.1.2探究二:我们再看图10.1.3中的两组图形.每一组里,某一边的图形沿虚线对折之后与另一边的图形完全重合.像这样,把一个图形沿着某一条直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形成轴对称,这条直线就是对称轴,两个图形中的对应点(即两个图形重合时互相重合的点)叫做对称点.做一做请你标出图10.1.3中A、B、C三点的对称点A1、B1、C1.试一试在纸上滴几滴墨水,把纸张对折,随后打开,看看形成的两块墨迹是不是关于折痕对称.画出它的对称轴.显然,轴对称图形(或成轴对称的两个图形)沿对称轴对折后的两部分是完全重合的,所以轴对称图形(或成轴对称的两个图形)的对应线段(对折后重合的线段)相等,对应角(对折后重合的角)相等. 思考自议以问题导入,吸引学生注意力,导入本节新课---生活中的轴对称. 引入新课,激发学生探究生活中的轴对称,从生活中观察轴对称的现象.
讲授新课 二、提炼概念三、典例精讲例:下面这些图形是轴对称图形吗?是,是,否 总结轴对称的现象和规律,激发学生探究轴对称的求知欲. 理解并讨论轴对称图形与两个图形成轴对称的区别和联系.
课堂练习 四、巩固训练1.甲骨文是我国的一种古代文字,下面是“北”“比”“鼎”“射”四个字的甲骨文,其中不是轴对称图形的是( )B2. 如图所示的图形中,左边图形与右边图形成轴对称的是( )D3.如图,直线MN是四边形AMBN的对称 轴,点P是直线MN上的点,下列判断错误的是( ) A.AM=BM B.AP=BN C.∠MAP=∠MBP D.∠ANM=∠BNMB4. 如图,AC=7,∠C=60°,△ABC与△A′B′C′关于直线l对称,则∠C′=________,A′C′=________.60° ,7 5.如下图,△ABC与△DEF关于直线 l轴对称,点P、Q、R分别是线段AD、BE、CF与直线l的交点.(1)如果AP=2cm,BQ=5cm ,你能说出DP、EQ的长吗?(2)如果线段AB=7cm,AC=5cm,你能说出DE、DF的长吗? 为什么?(3)由此,可以得出什么结论?
课堂小结 课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
