17.4 零指数幂和负整指数幂[下学期]
文档属性
| 名称 | 17.4 零指数幂和负整指数幂[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 524.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-27 19:55:00 | ||
图片预览








文档简介
课件26张PPT。北 师 大? 八 年 级《 数 学 ( 下 ) 》课首
17.4 零指数幂与负整指数幂教学目标、重点、难点理解零指数幂和负整指数幂的性质.理解和应用负整指数幂的性质。 理解和应用零指数幂与负整指数幂的性质一 、复习提问幂的运算性质: 【同底数幂相除的法则】不 忘 老 朋 友> 纳米技术是20世纪90年代出现的一门新兴技术。它是在0.10至100纳米尺度的空间内,研究电子、原子和分子运动规律和特性的崭新技术。
1纳米为十亿分之一米。也就是说
1米=1000000000纳米.
我们知道1米=1000000000纳米,可以简洁地表示为:1米=109纳米;
那么,反过来怎样简洁地表示
科 技 小 知 识?11…………1结论:……任何不等于零的数的零次幂都等于1.
【同底数幂的除法法则】【除法的意义】一、判断正误:
×√√√√二、计算
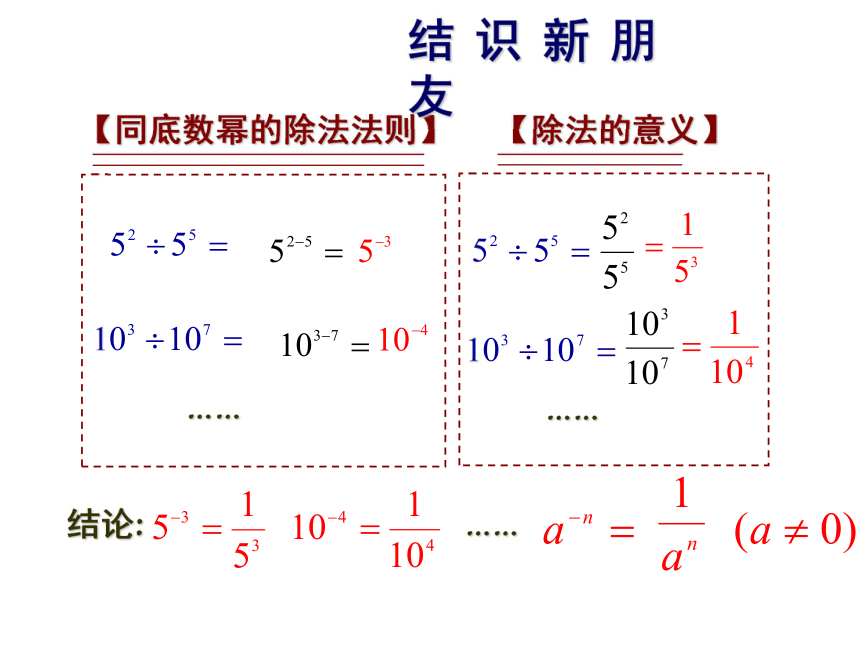
…………结论:……
【同底数幂的除法法则】【除法的意义】结 识 新 朋 友例题解析 任何不等于零的数的负整数次幂等于它的正整数次幂的倒数.3.用小数表示下列各数
10-4 2.1×10-52.填一填
-99=0.0001=0.000021解决问题随堂练习1.用小数或分数表示下列各数 今天我知道了……学会了……我能……任何不等于零的数的零次幂都等于1. 任何不等于零的数的负整数次幂等于它的正整数次幂的倒数. 问题1 在§21.1中介绍同底数幂的除法公式am÷an=am-n时,有一个附加条件:m>n,即被除数的指数大于除数的指数.当被除数的指数不大于除数的指数,即m=n或m<n时,情况怎样呢? 想一想讲解零指数幂的有关知识 先考察被除数的指数等于除数的指数的情况.例如考察下列算式:
52÷52,103÷103,a5÷a5(a≠0).
一方面,如果仿照同底数幂的除法公式来计算,得
52÷52=52-2=50,
103÷103=103-3=100,
a5÷a5=a5-5=a0(a≠0).
另一方面,由于这几个式子的被除式等于除式,由除法的意义可知,所得的商都等于1.我们规定:50=1,100=1,a0=1(a≠0).这就是说:
任何不等于零的数的零次幂都等于1.例2计算: 解: ⑴ ⑵例3、用小数表示下列各数:
(1)10-4; (2)2.1×10-5.=2.1×0.00001=0.000021.练 习:计算:判断下列式子是否成立?
17.4 零指数幂与负整指数幂教学目标、重点、难点理解零指数幂和负整指数幂的性质.理解和应用负整指数幂的性质。 理解和应用零指数幂与负整指数幂的性质一 、复习提问幂的运算性质: 【同底数幂相除的法则】不 忘 老 朋 友> 纳米技术是20世纪90年代出现的一门新兴技术。它是在0.10至100纳米尺度的空间内,研究电子、原子和分子运动规律和特性的崭新技术。
1纳米为十亿分之一米。也就是说
1米=1000000000纳米.
我们知道1米=1000000000纳米,可以简洁地表示为:1米=109纳米;
那么,反过来怎样简洁地表示
科 技 小 知 识?11…………1结论:……任何不等于零的数的零次幂都等于1.
【同底数幂的除法法则】【除法的意义】一、判断正误:
×√√√√二、计算
…………结论:……
【同底数幂的除法法则】【除法的意义】结 识 新 朋 友例题解析 任何不等于零的数的负整数次幂等于它的正整数次幂的倒数.3.用小数表示下列各数
10-4 2.1×10-52.填一填
-99=0.0001=0.000021解决问题随堂练习1.用小数或分数表示下列各数 今天我知道了……学会了……我能……任何不等于零的数的零次幂都等于1. 任何不等于零的数的负整数次幂等于它的正整数次幂的倒数. 问题1 在§21.1中介绍同底数幂的除法公式am÷an=am-n时,有一个附加条件:m>n,即被除数的指数大于除数的指数.当被除数的指数不大于除数的指数,即m=n或m<n时,情况怎样呢? 想一想讲解零指数幂的有关知识 先考察被除数的指数等于除数的指数的情况.例如考察下列算式:
52÷52,103÷103,a5÷a5(a≠0).
一方面,如果仿照同底数幂的除法公式来计算,得
52÷52=52-2=50,
103÷103=103-3=100,
a5÷a5=a5-5=a0(a≠0).
另一方面,由于这几个式子的被除式等于除式,由除法的意义可知,所得的商都等于1.我们规定:50=1,100=1,a0=1(a≠0).这就是说:
任何不等于零的数的零次幂都等于1.例2计算: 解: ⑴ ⑵例3、用小数表示下列各数:
(1)10-4; (2)2.1×10-5.=2.1×0.00001=0.000021.练 习:计算:判断下列式子是否成立?
