广西钦州市钦北区2022-2023学年高二下学期期中考试数学试题(含解析)
文档属性
| 名称 | 广西钦州市钦北区2022-2023学年高二下学期期中考试数学试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 472.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-29 05:31:04 | ||
图片预览




文档简介
钦州市钦北区2022-2023学年高二下学期期中考试
数 学
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.在等差数列中,,,则公差( )
A.1 B.2 C.-1 D.-2
2.设随机变量,则的值为( )
A.1.2 B.1.8 C.2.4 D.3.6
3.已知数列满足,,则( )
A. B. C.2 D.
4.已知等差数列的公差,前项和为,,则( )
A.6 B. C. D.8
5.通过随机调查140名性别不同的社区居民是否喜欢看电视剧, 得到如下的列联表:
男 女 总计
喜欢 50 40 90
不喜欢 20 30 50
总计 70 70 140
由公式算得:
附:,其中.
0.10 0.05 0.010 0.001
2.706 3.841 6.635 10.828
参照附表,得到的正确结论是( )
A.有的把握认为“居民是否喜欢看电视剧”与性别有关
B.有的把握认为“居民是否喜欢看电视剧”与性别有关
C.有的把握认为“居民是否喜欢看电视剧”与性别有关
D.有的把握认为“居民是否喜欢看电视剧”与性别有关
6.在某项测试中,测量结果服从正态分布,若,则( )
A.0.9 B.0.8 C.0.7 D.0.6
7.下表给出变量x,y的5组数据,为选出4组数据使得线性相关程度最大则应去掉
第1组 第2组 第3组 第4组 第5组
x 1 2 3 4 5
y 2.0 2.5 3.1 4.1 3.5
A.第1组数据 B.第3组数据 C.第4组数据 D.第5组数据
8.已知等差数列的前项和为,等差数列的前项和为,若,则( )
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.已知X的分布列为
X 0 1 2
P a
则下列说法正确的有( )
A. B.
C. D.
10.从甲袋中摸出一个红球的概率是,从乙袋中摸出一个红球的概率是,从两袋各摸出一个球,下列结论正确的是( )
A.2个球都是红球的概率为 B.2个球中恰有1个红球的概率为
C.2个球中至少有1个红球的概率为 D.2个球不都是红球的概率为
11.等差数列的公差为,前项和为,当首项和变化时,是一个定值,则下列各数也是定值的是( )
A. B. C. D.
12.一袋中有5个大小相同的黑球,编号为1,2,3,4,5,还有3个同样大小的白球,编号为6,7,8,现从中任取3个球,则下列结论中正确的是( )
A.取出的最小号码服从超几何分布
B.取出的白球个数服从超几何分布
C.取出2个黑球的概率为
D.若取出一个黑球记1分,取出一个白球记-1分,则总得分最小的概率为
三、填空题:本题共4小题,每小题5分,共20分.
13.观测两相关变量得如下数据
x 0.5 1 1.5 2 2.5 3 3.5
y 1 2 3 4 5 6 7
则两变量x,y间的回归直线必过点______.
14.甲、乙两人独立解同一道数学题目,甲解出这道题目的概率是,乙解出这道题目的概率是,这道题被解出的概率是______.
15.已知列联表如下:
温度低于30℃ 温度高于30℃ 总计
高产量 15 m 15+m
低产量 5 15 20
总计 20 15+m 35+m
若,则______.(附:,其中)
16.在前项和为的等差数列中,,,则______.
四、解答题:本题共6小题,共70分.解答应写出必要的文字说明、证明过程及演算步骤.
17.白黄瓜是一种比较常见的餐桌蔬菜,和普通的黄瓜不同,这种黄瓜的外观更加好看,颜色偏白,口感更好,所以在市面上拥有较高的价格.某农户一亩地种植白黄瓜,在所收成的黄瓜中,随机抽取并测量100条白黄瓜的长度(单位:厘米)和重量(单位:克),得到如下数据表:
单个黄瓜重量 单个黄瓜长
20 6 4
11 20 10
9 5 15
(1)根据所给的数据.完成下面的列联表;
单个黄瓜重量 单个黄瓜长 合计
合计
(2)根据(1)中的列联表,判断是否有的把握认为单个黄瓜重量与黄瓜长有关.附:,其中.
0.050 0.010 0.001
3.841 6.635 10.828
18.从有3个红球和4个黑球的盒子中,每次随机摸出一个球,摸出的球不再放回.求第2次摸到红球的概率.
19.已知等差数列的前项和为,,.
(1)求数列的通项公式;
(2)证明:当时,.
20.桃子是夏季最为常见的一种水果,它也是我国三大原生水果之一,并且地位很高,自古以来就有着“桃养人杏伤人”的说法.桃子在我国种植有数千年的历史了,并且种类也非常丰富.经一年的统计(加上桃子损耗),某农户种植桃子每千克投入的肥料费用(单位:元)与利润(单位:元)如下表所示:
x 2 4 6 8 10
y 1 1
(1)已知x与y线性相关,求y关于x的线性回归方程;
(2)在(1)的条件下,如果该农户预计明年该品种桃子每千克投入的肥料费用为5元,产量为1200千克,请估计该农户种植桃子的利润.
附:回归方程中的斜率和截距的最小二乘法估计公式分别为,,.
21.某商场为了了解顾客的购物信息,随机在商场收集了200位顾客购物的相关数据如下表:
一次购物款(单位:元)
顾客人数 20 a 50 60
(1)求的值;
(2)为了增加商场销售额度,对一次购物不低于300元的顾客每人发放一个纪念品.现有5人前去该商场购物,用频率估计概率,求获得纪念品的数量的分布列与数学期望.
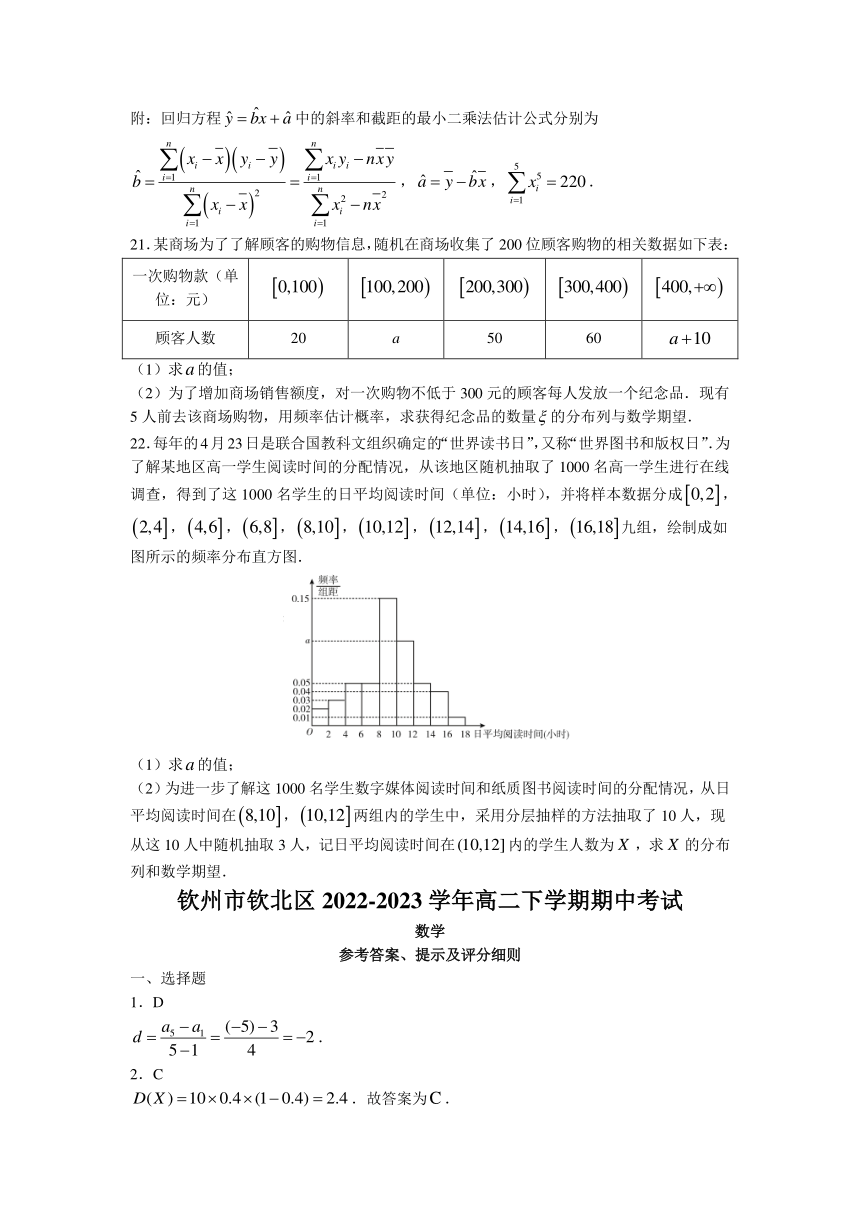
22.每年的4月23日是联合国教科文组织确定的“世界读书日”,又称“世界图书和版权日”.为了解某地区高一学生阅读时间的分配情况,从该地区随机抽取了1000名高一学生进行在线调查,得到了这1000名学生的日平均阅读时间(单位:小时),并将样本数据分成,,,,,,,,九组,绘制成如图所示的频率分布直方图.
(1)求的值;
(2)为进一步了解这1000名学生数字媒体阅读时间和纸质图书阅读时间的分配情况,从日平均阅读时间在,两组内的学生中,采用分层抽样的方法抽取了10人,现从这10人中随机抽取3人,记日平均阅读时间在内的学生人数为,求的分布列和数学期望.
钦州市钦北区2022-2023学年高二下学期期中考试
数学
参考答案、提示及评分细则
一、选择题
1.D
.
2.C
.故答案为.
3.A
,.
4.C
.
二、多选题
5.C
由,,故有的把握认为“居民是否喜欢看电视剧”与性别有关.
6.B
由正态分布的图象和性质得.故答案为B.
7.D
画出散点图如图所示,则应去掉第5组数据.
8.D
.
9.ABD
由分布列的性质可知,即,∴,故A正确;
,故 B 正确;
,故C不正确;
,故D正确.
10.ABC
A项,因为从甲袋中摸出一个红球的概率是,从乙袋中摸出一个红球的概率是,所以2个球都是红球的概率为,故正确;
B项,2个球中恰有1个红球的概率为,故正确;
C项,至少有1个红球的概率为,故正确;
D项,2个球不都是红球的概率为,故错误.
11.AC
由,可知为定值,,也为定值.
12.BC
对于A,超几何分布取出某个对象的结果数不定,也就是说超几何分布的随机变量为实验次数,即指某事件发生次的试验次数,由此可知取出的最大号码不服从超几何分布,故A错误;
对于B,超几何分布的随机变量为实验次数,即指某事件发生次的试验次数,由此可知取出的黑球个数服从超几何分布,故B正确;
对于C,取出2个黑球的概率为,故C正确;
对于D,若取出一个黑球记1分,取出一个白球记-1分,则取出三个白球的总得分最小,
∴总得分最大的概率为,故D不正确.故选BC.
13.(2,4)
由,,则两变量,间的回归直线必过点(2,4).
14.
设“甲解出这道题目”为事件A,“乙解出这道题目”为事件B,则,,则这道题被解出的概率为.
15.5
由,解得.
16.27
由,有,又由,有.
17.解:(1)完成列联表如下:
单个黄瓜重量 单个黄瓜长 合计
20 10 30
20 50 70
合计 40 60 100
(2),
故能有的把握认为单个黄瓜重量与黄瓜长有关.
18.解:用表示第一次摸到红球,表示第二次摸到红球,表示第一次摸到黑球,表示第二次摸到黑球.
则
.
19.解:(1)设等差数列的公差为d
由题意有,解得.
所以,故数列的通项公式为;
(2)由(1)有,
所以,故当时,.
20.解:(1)由,
,
,
有,,
故关于的线性回归方程为;
(2)当时,,
明年一年,该农户种植桃子的利润为(元).
21.解:(1)由题意有,
解得,故的值为30;
(2)由(1)可知1人购物获得纪念品的频率即为概率,
故5人购物获得纪念品的数量服从二项分配,
则,
,
,
,
,
.
则的分布列为:
0 1 2 3 4 5
P
的数学期望为.
22.解:(1)由频率分布直方图得:
,解得;
(2)由频率分布直方图得:
这1000名学生中日平均阅读时间在,两组内的学生人数之比为,
若采用分层抽样的方法抽取了10人,
则从日平均阅读时间在内的学生中抽取(人),
在日平均阅读时间在内的学生中抽取4人,
现从这10人中随机抽取3人,则的可能取值为0,1,2,3,
,
,
,
,
∴X的分布列为:
X 0 1 2 3
P
.
数 学
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.在等差数列中,,,则公差( )
A.1 B.2 C.-1 D.-2
2.设随机变量,则的值为( )
A.1.2 B.1.8 C.2.4 D.3.6
3.已知数列满足,,则( )
A. B. C.2 D.
4.已知等差数列的公差,前项和为,,则( )
A.6 B. C. D.8
5.通过随机调查140名性别不同的社区居民是否喜欢看电视剧, 得到如下的列联表:
男 女 总计
喜欢 50 40 90
不喜欢 20 30 50
总计 70 70 140
由公式算得:
附:,其中.
0.10 0.05 0.010 0.001
2.706 3.841 6.635 10.828
参照附表,得到的正确结论是( )
A.有的把握认为“居民是否喜欢看电视剧”与性别有关
B.有的把握认为“居民是否喜欢看电视剧”与性别有关
C.有的把握认为“居民是否喜欢看电视剧”与性别有关
D.有的把握认为“居民是否喜欢看电视剧”与性别有关
6.在某项测试中,测量结果服从正态分布,若,则( )
A.0.9 B.0.8 C.0.7 D.0.6
7.下表给出变量x,y的5组数据,为选出4组数据使得线性相关程度最大则应去掉
第1组 第2组 第3组 第4组 第5组
x 1 2 3 4 5
y 2.0 2.5 3.1 4.1 3.5
A.第1组数据 B.第3组数据 C.第4组数据 D.第5组数据
8.已知等差数列的前项和为,等差数列的前项和为,若,则( )
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.已知X的分布列为
X 0 1 2
P a
则下列说法正确的有( )
A. B.
C. D.
10.从甲袋中摸出一个红球的概率是,从乙袋中摸出一个红球的概率是,从两袋各摸出一个球,下列结论正确的是( )
A.2个球都是红球的概率为 B.2个球中恰有1个红球的概率为
C.2个球中至少有1个红球的概率为 D.2个球不都是红球的概率为
11.等差数列的公差为,前项和为,当首项和变化时,是一个定值,则下列各数也是定值的是( )
A. B. C. D.
12.一袋中有5个大小相同的黑球,编号为1,2,3,4,5,还有3个同样大小的白球,编号为6,7,8,现从中任取3个球,则下列结论中正确的是( )
A.取出的最小号码服从超几何分布
B.取出的白球个数服从超几何分布
C.取出2个黑球的概率为
D.若取出一个黑球记1分,取出一个白球记-1分,则总得分最小的概率为
三、填空题:本题共4小题,每小题5分,共20分.
13.观测两相关变量得如下数据
x 0.5 1 1.5 2 2.5 3 3.5
y 1 2 3 4 5 6 7
则两变量x,y间的回归直线必过点______.
14.甲、乙两人独立解同一道数学题目,甲解出这道题目的概率是,乙解出这道题目的概率是,这道题被解出的概率是______.
15.已知列联表如下:
温度低于30℃ 温度高于30℃ 总计
高产量 15 m 15+m
低产量 5 15 20
总计 20 15+m 35+m
若,则______.(附:,其中)
16.在前项和为的等差数列中,,,则______.
四、解答题:本题共6小题,共70分.解答应写出必要的文字说明、证明过程及演算步骤.
17.白黄瓜是一种比较常见的餐桌蔬菜,和普通的黄瓜不同,这种黄瓜的外观更加好看,颜色偏白,口感更好,所以在市面上拥有较高的价格.某农户一亩地种植白黄瓜,在所收成的黄瓜中,随机抽取并测量100条白黄瓜的长度(单位:厘米)和重量(单位:克),得到如下数据表:
单个黄瓜重量 单个黄瓜长
20 6 4
11 20 10
9 5 15
(1)根据所给的数据.完成下面的列联表;
单个黄瓜重量 单个黄瓜长 合计
合计
(2)根据(1)中的列联表,判断是否有的把握认为单个黄瓜重量与黄瓜长有关.附:,其中.
0.050 0.010 0.001
3.841 6.635 10.828
18.从有3个红球和4个黑球的盒子中,每次随机摸出一个球,摸出的球不再放回.求第2次摸到红球的概率.
19.已知等差数列的前项和为,,.
(1)求数列的通项公式;
(2)证明:当时,.
20.桃子是夏季最为常见的一种水果,它也是我国三大原生水果之一,并且地位很高,自古以来就有着“桃养人杏伤人”的说法.桃子在我国种植有数千年的历史了,并且种类也非常丰富.经一年的统计(加上桃子损耗),某农户种植桃子每千克投入的肥料费用(单位:元)与利润(单位:元)如下表所示:
x 2 4 6 8 10
y 1 1
(1)已知x与y线性相关,求y关于x的线性回归方程;
(2)在(1)的条件下,如果该农户预计明年该品种桃子每千克投入的肥料费用为5元,产量为1200千克,请估计该农户种植桃子的利润.
附:回归方程中的斜率和截距的最小二乘法估计公式分别为,,.
21.某商场为了了解顾客的购物信息,随机在商场收集了200位顾客购物的相关数据如下表:
一次购物款(单位:元)
顾客人数 20 a 50 60
(1)求的值;
(2)为了增加商场销售额度,对一次购物不低于300元的顾客每人发放一个纪念品.现有5人前去该商场购物,用频率估计概率,求获得纪念品的数量的分布列与数学期望.
22.每年的4月23日是联合国教科文组织确定的“世界读书日”,又称“世界图书和版权日”.为了解某地区高一学生阅读时间的分配情况,从该地区随机抽取了1000名高一学生进行在线调查,得到了这1000名学生的日平均阅读时间(单位:小时),并将样本数据分成,,,,,,,,九组,绘制成如图所示的频率分布直方图.
(1)求的值;
(2)为进一步了解这1000名学生数字媒体阅读时间和纸质图书阅读时间的分配情况,从日平均阅读时间在,两组内的学生中,采用分层抽样的方法抽取了10人,现从这10人中随机抽取3人,记日平均阅读时间在内的学生人数为,求的分布列和数学期望.
钦州市钦北区2022-2023学年高二下学期期中考试
数学
参考答案、提示及评分细则
一、选择题
1.D
.
2.C
.故答案为.
3.A
,.
4.C
.
二、多选题
5.C
由,,故有的把握认为“居民是否喜欢看电视剧”与性别有关.
6.B
由正态分布的图象和性质得.故答案为B.
7.D
画出散点图如图所示,则应去掉第5组数据.
8.D
.
9.ABD
由分布列的性质可知,即,∴,故A正确;
,故 B 正确;
,故C不正确;
,故D正确.
10.ABC
A项,因为从甲袋中摸出一个红球的概率是,从乙袋中摸出一个红球的概率是,所以2个球都是红球的概率为,故正确;
B项,2个球中恰有1个红球的概率为,故正确;
C项,至少有1个红球的概率为,故正确;
D项,2个球不都是红球的概率为,故错误.
11.AC
由,可知为定值,,也为定值.
12.BC
对于A,超几何分布取出某个对象的结果数不定,也就是说超几何分布的随机变量为实验次数,即指某事件发生次的试验次数,由此可知取出的最大号码不服从超几何分布,故A错误;
对于B,超几何分布的随机变量为实验次数,即指某事件发生次的试验次数,由此可知取出的黑球个数服从超几何分布,故B正确;
对于C,取出2个黑球的概率为,故C正确;
对于D,若取出一个黑球记1分,取出一个白球记-1分,则取出三个白球的总得分最小,
∴总得分最大的概率为,故D不正确.故选BC.
13.(2,4)
由,,则两变量,间的回归直线必过点(2,4).
14.
设“甲解出这道题目”为事件A,“乙解出这道题目”为事件B,则,,则这道题被解出的概率为.
15.5
由,解得.
16.27
由,有,又由,有.
17.解:(1)完成列联表如下:
单个黄瓜重量 单个黄瓜长 合计
20 10 30
20 50 70
合计 40 60 100
(2),
故能有的把握认为单个黄瓜重量与黄瓜长有关.
18.解:用表示第一次摸到红球,表示第二次摸到红球,表示第一次摸到黑球,表示第二次摸到黑球.
则
.
19.解:(1)设等差数列的公差为d
由题意有,解得.
所以,故数列的通项公式为;
(2)由(1)有,
所以,故当时,.
20.解:(1)由,
,
,
有,,
故关于的线性回归方程为;
(2)当时,,
明年一年,该农户种植桃子的利润为(元).
21.解:(1)由题意有,
解得,故的值为30;
(2)由(1)可知1人购物获得纪念品的频率即为概率,
故5人购物获得纪念品的数量服从二项分配,
则,
,
,
,
,
.
则的分布列为:
0 1 2 3 4 5
P
的数学期望为.
22.解:(1)由频率分布直方图得:
,解得;
(2)由频率分布直方图得:
这1000名学生中日平均阅读时间在,两组内的学生人数之比为,
若采用分层抽样的方法抽取了10人,
则从日平均阅读时间在内的学生中抽取(人),
在日平均阅读时间在内的学生中抽取4人,
现从这10人中随机抽取3人,则的可能取值为0,1,2,3,
,
,
,
,
∴X的分布列为:
X 0 1 2 3
P
.
同课章节目录
