八年级下学期十七章直角平面坐标系[下学期]
文档属性
| 名称 | 八年级下学期十七章直角平面坐标系[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 417.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-10 09:28:00 | ||
图片预览



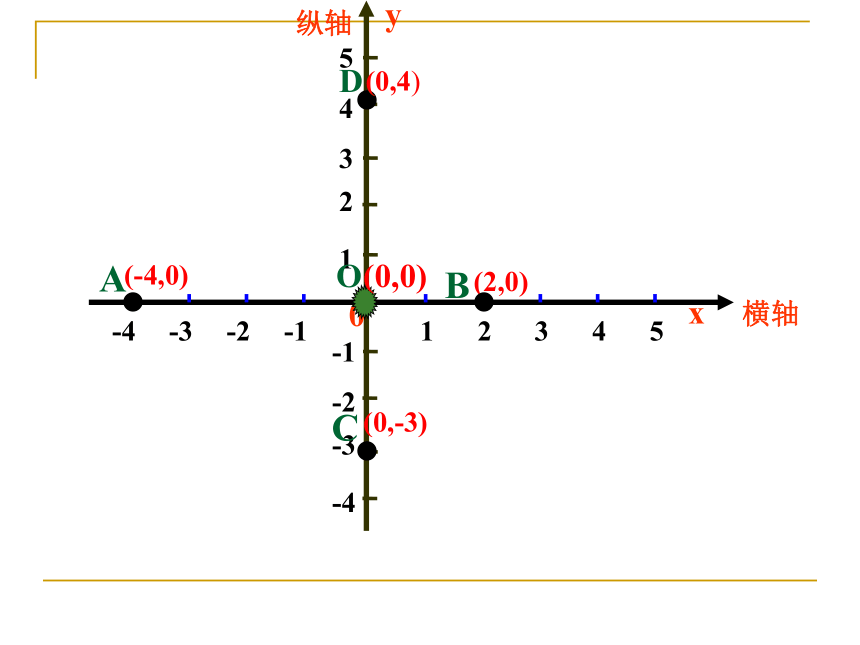
文档简介
课件16张PPT。17.2函数的图象0 2 4 6 8 10 12 14 16 18 20 22 24 t(时)Y (°C)
12
10
8
6
4
2
-2
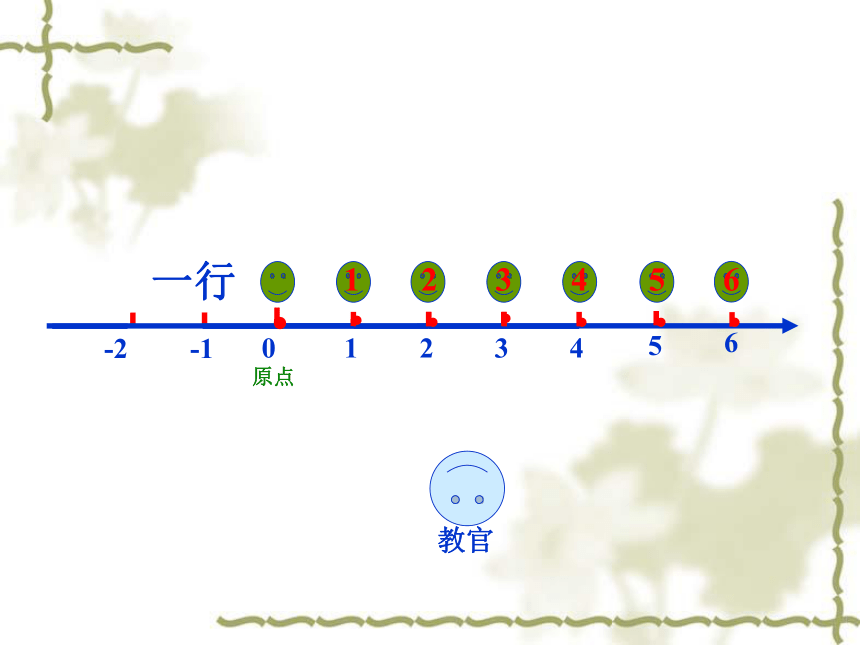
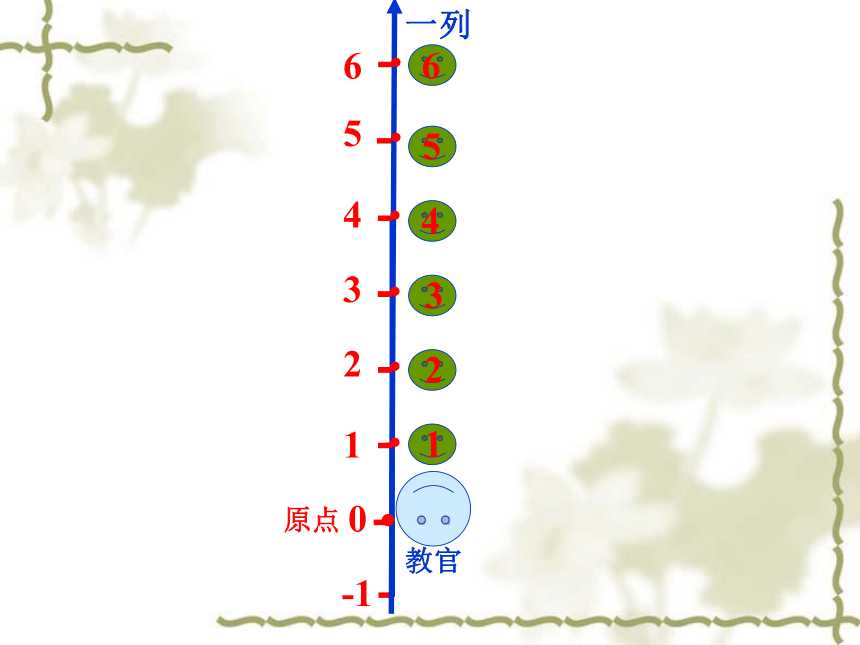
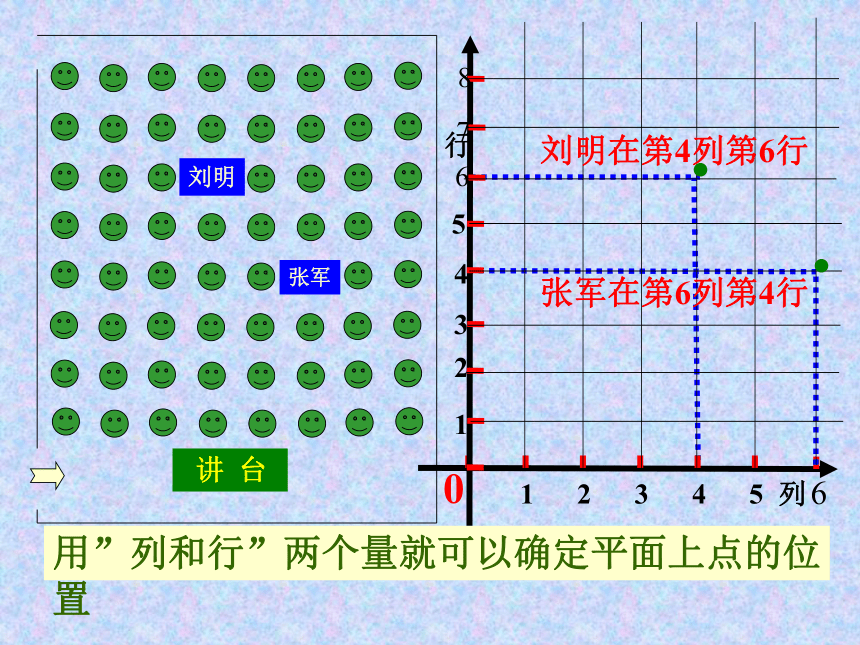
-4平面直角坐标系某地一天内的气温变化图123456 一行教官······123456原点一列教官 讲 台刘明张军刘明在第4列第6行张军在第6列第4行用”列和行”两个量就可以确定平面上点的位置··第一象限第四象限第三象限第二象限平面直角坐标系·PP点在x 轴上对应的数为3P点在y 轴上对应的数为2P点在平面直角坐标系中的坐标
记作:(2,3)(-2,3)(3,-2)(3,2)P(3,2)(+,+)(-,+)(-,-)(+,-)··MN???ABCD(2,0)O(-4,0)(0,0)(0,-3)(0,4)? 点A(2,-3)在第 象限;
点C(-2,3)在第 象限;
点E(2,0)在 上;
点F(0,-3)在 上。比一比四二X轴 Y轴 已知点P(X,Y),若XY>0,则点P在
象限,若XY<0,则点P 在 象限;若XY=O则点P 在 上.第一或第三第二或第四坐标轴 在平面直角坐标系中,描出下列各点.xy -4 -3 -2 -1 0 1 2 3 4 O4
3
2
1-1
-2
-3
-4.B(-2,3).C(2,3).A(-4,4)试一试A(-4,4)
B(-2,3)
C(2,3)
D(4,4)
E(-2,-3)
F(2,-3)
.D(4,4).F(2,-3).E(-2,-3)已知点P(3,-4),
P点关于X轴的对称点P1的坐标是 ;
P点关于Y轴的对称点P2的坐标是 ;
P点关于原点的对称点P3的坐标是 。想一想(3,4)(-3,-4)(-3,4)已知点P(a,b),
P点关于X轴的对称点P1的坐标是 ;
P点关于Y轴的对称点P2的坐标是 ;
P点关于原点的对称点P3的坐标是 。
(-a,-b)(-a,b)(a,-b)练 习(教科书31页练习1):
在直角坐标系中描出点A(2,-3),分别找出它关于x轴、y轴及坐标原点的对称点,并写出这些点的坐标.
如图所示的国际
象棋的棋盘中,双方四只
马的位置分别是
A(b,3)、B(d、5)
C(f,7)、D(h,2)
请在图中描出它们的位置.练习(教科书31页练习2) 笛卡儿是著名的法国数学家,他用平面上的一点到两条固定直线的距离来确定点的距离,用坐标来描述平面和空间上的点,他进而创立了解析几何学,表明了几何问题不仅可以归结成为代数形式,而且可以通过代数变换来发现几何性质,证明几何性质代数 几何 坐 标作业:教科书第37页习题1、2题做在本上第3题做在书上谢谢指导! 通过本节课的学习知道:平面内的点可由两条数轴上的点(即平面直角坐标系)来表示.有了平面直角坐标系,就可以把两个相依变化的量之间的变化规律,用图形非常形象地表示出来,,因此平面直角坐标系成了研究两个变量的有利工具。如:第一张幻灯片就是利用平面直角坐标描述了气温随着时间的变化情况,有利于指导科研、生产和生活。同学们在平常的学习中要多动脑,大胆地想.要知道早在1637年以前,代数和几何是两个不同的研究领域,当时的代数完全从属于公式和法则,几何过于依赖图形,笛卡尔不满足于代数和几何彼此分离的状况,因此他提出必须把代数和几何的优点结合起来,建立一种"真正的数学",根据这种思想他创立了直角坐标系,进而创立了解析几何,从而打开了近代数学的大门,为一大批数学家的新发现开辟了道路,在科学史上具有划时代的意义。同学们在平常的学习中要多动脑,大胆地想,说不定今后在座的同学中会涌现一位或多位数学家呢! 小结
12
10
8
6
4
2
-2
-4平面直角坐标系某地一天内的气温变化图123456 一行教官······123456原点一列教官 讲 台刘明张军刘明在第4列第6行张军在第6列第4行用”列和行”两个量就可以确定平面上点的位置··第一象限第四象限第三象限第二象限平面直角坐标系·PP点在x 轴上对应的数为3P点在y 轴上对应的数为2P点在平面直角坐标系中的坐标
记作:(2,3)(-2,3)(3,-2)(3,2)P(3,2)(+,+)(-,+)(-,-)(+,-)··MN???ABCD(2,0)O(-4,0)(0,0)(0,-3)(0,4)? 点A(2,-3)在第 象限;
点C(-2,3)在第 象限;
点E(2,0)在 上;
点F(0,-3)在 上。比一比四二X轴 Y轴 已知点P(X,Y),若XY>0,则点P在
象限,若XY<0,则点P 在 象限;若XY=O则点P 在 上.第一或第三第二或第四坐标轴 在平面直角坐标系中,描出下列各点.xy -4 -3 -2 -1 0 1 2 3 4 O4
3
2
1-1
-2
-3
-4.B(-2,3).C(2,3).A(-4,4)试一试A(-4,4)
B(-2,3)
C(2,3)
D(4,4)
E(-2,-3)
F(2,-3)
.D(4,4).F(2,-3).E(-2,-3)已知点P(3,-4),
P点关于X轴的对称点P1的坐标是 ;
P点关于Y轴的对称点P2的坐标是 ;
P点关于原点的对称点P3的坐标是 。想一想(3,4)(-3,-4)(-3,4)已知点P(a,b),
P点关于X轴的对称点P1的坐标是 ;
P点关于Y轴的对称点P2的坐标是 ;
P点关于原点的对称点P3的坐标是 。
(-a,-b)(-a,b)(a,-b)练 习(教科书31页练习1):
在直角坐标系中描出点A(2,-3),分别找出它关于x轴、y轴及坐标原点的对称点,并写出这些点的坐标.
如图所示的国际
象棋的棋盘中,双方四只
马的位置分别是
A(b,3)、B(d、5)
C(f,7)、D(h,2)
请在图中描出它们的位置.练习(教科书31页练习2) 笛卡儿是著名的法国数学家,他用平面上的一点到两条固定直线的距离来确定点的距离,用坐标来描述平面和空间上的点,他进而创立了解析几何学,表明了几何问题不仅可以归结成为代数形式,而且可以通过代数变换来发现几何性质,证明几何性质代数 几何 坐 标作业:教科书第37页习题1、2题做在本上第3题做在书上谢谢指导! 通过本节课的学习知道:平面内的点可由两条数轴上的点(即平面直角坐标系)来表示.有了平面直角坐标系,就可以把两个相依变化的量之间的变化规律,用图形非常形象地表示出来,,因此平面直角坐标系成了研究两个变量的有利工具。如:第一张幻灯片就是利用平面直角坐标描述了气温随着时间的变化情况,有利于指导科研、生产和生活。同学们在平常的学习中要多动脑,大胆地想.要知道早在1637年以前,代数和几何是两个不同的研究领域,当时的代数完全从属于公式和法则,几何过于依赖图形,笛卡尔不满足于代数和几何彼此分离的状况,因此他提出必须把代数和几何的优点结合起来,建立一种"真正的数学",根据这种思想他创立了直角坐标系,进而创立了解析几何,从而打开了近代数学的大门,为一大批数学家的新发现开辟了道路,在科学史上具有划时代的意义。同学们在平常的学习中要多动脑,大胆地想,说不定今后在座的同学中会涌现一位或多位数学家呢! 小结
