【全国百强校】东北师大附中高中数学必修一导学案:222 对数函数及其性质
文档属性
| 名称 | 【全国百强校】东北师大附中高中数学必修一导学案:222 对数函数及其性质 |

|
|
| 格式 | zip | ||
| 文件大小 | 49.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-06-21 06:03:02 | ||
图片预览


文档简介
东北师范大学附属中学
学科:数学 年级:高一 编稿老师:邢昌振
审稿老师:王艳平
[同步教学信息]
2.2.2 对数函数及其性质
【教材阅读提示】函数源于实际生活.我们在研究指数函数时,曾经讨论过细胞分裂问题,
得到的细胞案的个数y是分裂次数x的函数指数函数,即y=2x. 我们现在要思考的是:
(1)如果要求这种细胞经过多少次分裂,大约可以得到1万个,10万个……细胞,那么,分裂次数x就是要得到的细胞个数y的函数,从而到的函数如何表示,它和指数函数有什么关系?
(2)此函数有哪些基本性质 ?
【基础知识精讲】
(一)教学知识点
知识目标:1.对数函数的概念、对数函数的单调性;
2.对数函数的图象和性质;
3.对数形式的复合函数的单调性;
4.同底数对数、不同底对数的大小的比较.
能力目标:1.理解对数函数的概念,掌握对数函数的图象和性质;
2.掌握同底对数、不同底对数的大小的比较方法;
3.掌握对数形式复合函数的单调性的判断及证明方法;
情感、态度、价值观:1.用联系的观点分析问题;
2.认识事物之间的相互转化;
教学重点:掌握对数函数的图象和性质.
教学难点:对数函数的定义,对数函数的图象和性质及应用.
(二)知识框架图
(三)知识点精讲
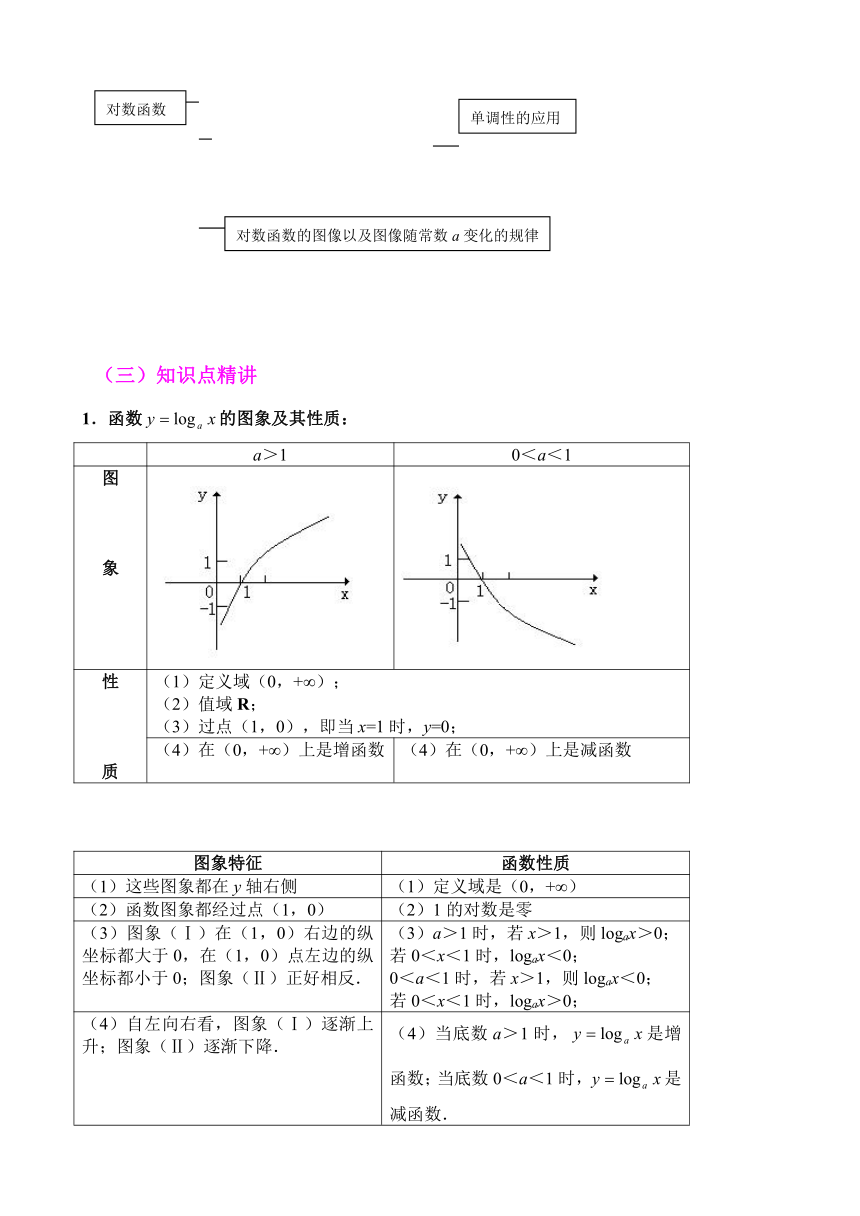
1.函数的图象及其性质:
a>1
0<a<1
图
象
性
质
(1)定义域(0,+∞);
(2)值域R;
(3)过点(1,0),即当x=1时,y=0;
(4)在(0,+∞)上是增函数
(4)在(0,+∞)上是减函数
图象特征
函数性质
(1)这些图象都在y轴右侧
(1)定义域是(0,+∞)
(2)函数图象都经过点(1,0)
(2)1的对数是零
(3)图象(Ⅰ)在(1,0)右边的纵坐标都大于0,在(1,0)点左边的纵坐标都小于0;图象(Ⅱ)正好相反.
(3)a>1时,若x>1,则logax>0;
若0<x<1时,logax<0;
0<a<1时,若x>1,则logax<0;
若0<x<1时,logax>0;
(4)自左向右看,图象(Ⅰ)逐渐上升;图象(Ⅱ)逐渐下降.
(4)当底数a>1时,是增函数;当底数0<a<1时,是减函数.
对数函数的定义域、值域分别为相应的指数函数的值域和定义域,它们的图象关于直线y=x对称;
(1,0)为所有对数函数图象的交汇点;
和指数函数的单调性一样,当a>1时,y=logax在(0,+∞)上是增函数,当0<a<1时,y=logax在(0,+∞)上是减函数.
【应用举例】
【例 1】求下列函数的定义域:
y=logax2; (2)y=loga(4-x); (3)y=loga(9-x2);
(4); .
解:(1)∵x2>0,∴x≠0,∴定义域是{x|x∈R且x≠0};
(2)∵4-x>0,∴x<4,∴定义域是{x|x<4(;
(3)∵9-x2>0,∴-3<x<3,∴定义域是{x|-3<x<3(;
(4),∴定义域是{x|0<x≤1(;
(5)∵log5x≠0,∴log5x≠log51,∴x≠1,∴定义域为{x|x≠1}.
求函数定义域方法小结:
分母不能为零;
偶次方根的被开方数大于或等于零;
对数的真数必须大于零;
指数函数、对数函数的底数要求大于零且不等于1.
【例 2】比较下列各组数中两个值的大小:
(4)log76,log67 ; (5)log3(,log20.8.
解:(1)考察对数函数y=log2x,
∵2>1,∴y=log2x在(0,+∞)上是增函数,
∴log23.4<log28.5.
(2)考察对数函数y=log0.3x,
∵0.3<1,∴y=log0.3x在(0,+∞)上是减函数,
∴.
(3)由于两个对数的底数a大小不一定,而a的大小直接影响函数的单调性,因此要对底数进行讨论:
当a>1时,y=logax在(0,+∞)上是增函数,∴;
当0<a<1时,y=logax在(0,+∞)上是减函数,∴.
(4)∵log76>log66=1,log67<log77=1,∴log76>log67.
(5)∵log3(>log31=0,log20.8<log21=0,∴log3(>log20.8.
小结:
1.当比较的对数值是底数相同的情况时,只需考虑相应对数函数的单调性,利用函数的单调性来判断大小;当比较的数值是底数不相同的情况时,常常需要引入中间值(例如0或1)来间接比较它们的大小;
2.对于logab的正负性,可直接利用下列性质来判断:
若a>1,b>1,或0<a<1,0<b<1时,logab>0;
若a>1,0<b<1或b>1,0<a<1时,logab<0.
【例3】证明函数上是增函数;并判断
上是增函数还是减函数?
分析:此题目的是在于让学生熟悉函数单调性证明的通法,同时熟悉利用对数函数的单调性比较同底数对数大小的方法.
证明:
∴函数上是增函数;
同理可证函数上是减函数.
【自我检测】
【同步训练初级】
1.四个函数分别为①;②;③;④. 其图象关于原点对称的是 ( )
A.②和③ B.①和② C.②和④ D.①和②、③和④
2.已知函数的定义域为F,函数的定义域为G,那么 ( ) A. B. F=G C. F G D.FG
3.将log0。70.8,log1.10.9,1.10。9按照从小到大的顺序排列.
4.比较下列各组数的大小关系:
;
.
5.已知全集I=R,,则= ( ) A. B.
C. D.
【同步训练高级】
6.若,则a的取值范围是 ( )
A. B.
C. D.
7.求下列函数的定义域:
(1).
8.已知=loga(2-ax)在[0,1]上是减函数,求a的取值范围.
参考答案
1.D
2.D
3.解:∵log1.10.9<log1.11=0,
log0。70.8>log0。71=0,又log0。70.8<log0。70.7=1,由指数函数的单调性可知
1.10。9>1.10=1, ∴log0。70.8<1.10。9.
∴ 从小到大的排列是:log1.10.9<log0。70.8<1.10。9.
4.
5.B
6.B
7.(1)(-3,-2)∪(-2,1(;
(2).
8.
∴a>1,
学科:数学 年级:高一 编稿老师:邢昌振
审稿老师:王艳平
[同步教学信息]
2.2.2 对数函数及其性质
【教材阅读提示】函数源于实际生活.我们在研究指数函数时,曾经讨论过细胞分裂问题,
得到的细胞案的个数y是分裂次数x的函数指数函数,即y=2x. 我们现在要思考的是:
(1)如果要求这种细胞经过多少次分裂,大约可以得到1万个,10万个……细胞,那么,分裂次数x就是要得到的细胞个数y的函数,从而到的函数如何表示,它和指数函数有什么关系?
(2)此函数有哪些基本性质 ?
【基础知识精讲】
(一)教学知识点
知识目标:1.对数函数的概念、对数函数的单调性;
2.对数函数的图象和性质;
3.对数形式的复合函数的单调性;
4.同底数对数、不同底对数的大小的比较.
能力目标:1.理解对数函数的概念,掌握对数函数的图象和性质;
2.掌握同底对数、不同底对数的大小的比较方法;
3.掌握对数形式复合函数的单调性的判断及证明方法;
情感、态度、价值观:1.用联系的观点分析问题;
2.认识事物之间的相互转化;
教学重点:掌握对数函数的图象和性质.
教学难点:对数函数的定义,对数函数的图象和性质及应用.
(二)知识框架图
(三)知识点精讲
1.函数的图象及其性质:
a>1
0<a<1
图
象
性
质
(1)定义域(0,+∞);
(2)值域R;
(3)过点(1,0),即当x=1时,y=0;
(4)在(0,+∞)上是增函数
(4)在(0,+∞)上是减函数
图象特征
函数性质
(1)这些图象都在y轴右侧
(1)定义域是(0,+∞)
(2)函数图象都经过点(1,0)
(2)1的对数是零
(3)图象(Ⅰ)在(1,0)右边的纵坐标都大于0,在(1,0)点左边的纵坐标都小于0;图象(Ⅱ)正好相反.
(3)a>1时,若x>1,则logax>0;
若0<x<1时,logax<0;
0<a<1时,若x>1,则logax<0;
若0<x<1时,logax>0;
(4)自左向右看,图象(Ⅰ)逐渐上升;图象(Ⅱ)逐渐下降.
(4)当底数a>1时,是增函数;当底数0<a<1时,是减函数.
对数函数的定义域、值域分别为相应的指数函数的值域和定义域,它们的图象关于直线y=x对称;
(1,0)为所有对数函数图象的交汇点;
和指数函数的单调性一样,当a>1时,y=logax在(0,+∞)上是增函数,当0<a<1时,y=logax在(0,+∞)上是减函数.
【应用举例】
【例 1】求下列函数的定义域:
y=logax2; (2)y=loga(4-x); (3)y=loga(9-x2);
(4); .
解:(1)∵x2>0,∴x≠0,∴定义域是{x|x∈R且x≠0};
(2)∵4-x>0,∴x<4,∴定义域是{x|x<4(;
(3)∵9-x2>0,∴-3<x<3,∴定义域是{x|-3<x<3(;
(4),∴定义域是{x|0<x≤1(;
(5)∵log5x≠0,∴log5x≠log51,∴x≠1,∴定义域为{x|x≠1}.
求函数定义域方法小结:
分母不能为零;
偶次方根的被开方数大于或等于零;
对数的真数必须大于零;
指数函数、对数函数的底数要求大于零且不等于1.
【例 2】比较下列各组数中两个值的大小:
(4)log76,log67 ; (5)log3(,log20.8.
解:(1)考察对数函数y=log2x,
∵2>1,∴y=log2x在(0,+∞)上是增函数,
∴log23.4<log28.5.
(2)考察对数函数y=log0.3x,
∵0.3<1,∴y=log0.3x在(0,+∞)上是减函数,
∴.
(3)由于两个对数的底数a大小不一定,而a的大小直接影响函数的单调性,因此要对底数进行讨论:
当a>1时,y=logax在(0,+∞)上是增函数,∴;
当0<a<1时,y=logax在(0,+∞)上是减函数,∴.
(4)∵log76>log66=1,log67<log77=1,∴log76>log67.
(5)∵log3(>log31=0,log20.8<log21=0,∴log3(>log20.8.
小结:
1.当比较的对数值是底数相同的情况时,只需考虑相应对数函数的单调性,利用函数的单调性来判断大小;当比较的数值是底数不相同的情况时,常常需要引入中间值(例如0或1)来间接比较它们的大小;
2.对于logab的正负性,可直接利用下列性质来判断:
若a>1,b>1,或0<a<1,0<b<1时,logab>0;
若a>1,0<b<1或b>1,0<a<1时,logab<0.
【例3】证明函数上是增函数;并判断
上是增函数还是减函数?
分析:此题目的是在于让学生熟悉函数单调性证明的通法,同时熟悉利用对数函数的单调性比较同底数对数大小的方法.
证明:
∴函数上是增函数;
同理可证函数上是减函数.
【自我检测】
【同步训练初级】
1.四个函数分别为①;②;③;④. 其图象关于原点对称的是 ( )
A.②和③ B.①和② C.②和④ D.①和②、③和④
2.已知函数的定义域为F,函数的定义域为G,那么 ( ) A. B. F=G C. F G D.FG
3.将log0。70.8,log1.10.9,1.10。9按照从小到大的顺序排列.
4.比较下列各组数的大小关系:
;
.
5.已知全集I=R,,则= ( ) A. B.
C. D.
【同步训练高级】
6.若,则a的取值范围是 ( )
A. B.
C. D.
7.求下列函数的定义域:
(1).
8.已知=loga(2-ax)在[0,1]上是减函数,求a的取值范围.
参考答案
1.D
2.D
3.解:∵log1.10.9<log1.11=0,
log0。70.8>log0。71=0,又log0。70.8<log0。70.7=1,由指数函数的单调性可知
1.10。9>1.10=1, ∴log0。70.8<1.10。9.
∴ 从小到大的排列是:log1.10.9<log0。70.8<1.10。9.
4.
5.B
6.B
7.(1)(-3,-2)∪(-2,1(;
(2).
8.
∴a>1,
