17.1 勾股定理(1)教案
文档属性
| 名称 | 17.1 勾股定理(1)教案 |  | |
| 格式 | zip | ||
| 文件大小 | 277.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-06-23 16:21:27 | ||
图片预览

文档简介
17.1勾股定理(1)
一、教材地位
本节课是人教版八年级下册第十七章第一节“ ( http: / / www.21cnjy.com )勾股定理”的第一课时.在本节课以前,学生已经学习了有关三角形的一些知识,也经历过利用图形面积来探求数式运算规律的过程。在探求勾股定理的过程中,蕴涵了丰富的数学思想.把三角形有一个直角“形”的特点转化为三边之间的“数”的关系,是数形结合的典范;把探求边的关系转化为探求面积的关系,将边不在格线上的图形转化为可计算的格点图形,是转化思想的体现;先探求特殊的直角三角形的三边关系,再探求一般直角三角形的三边关系,这是特殊——一般的思想.本节课,通过提供学生活动的方案,让学生在活动中思考,在思考中创新
二、教学目标
(一)知识与能力:
1.了解勾股定理的文化背景,体验勾股定理的探索过程
2.在勾股定理的探索过程中,发展合情推理能力,体会数形结合的思想
(二)过程与方法:
1.通过拼图活动,体验数学思维的严谨性,发展形象思维
2.在探究活动中,学会与人合作并能与他人交流思维的过程和探究结果
(三)情感态度价值观:
1.通过对勾股定理历史的了解,感受数学文化,激发学习热情
2.在探究活动中,体验解决问题方法的多样性,培养学生的合作交流意识和探索精神
三、教学重点与难点
重点:探索和证明勾股定理
难点:用拼图的方法证明勾股定理
四、课时安排及教具准备:一课时(45分钟)及一张卡片
五、 教学过程:
(一)引入新知、创设情境(2分钟)
以中国最早的一部数学著作——《周髀算经》的开头为引,介绍周公向商高请教数学知识时的对话,为勾股定理的出现埋下伏笔.
周公问:“窃闻乎大夫善数也,请问古者包牺立 ( http: / / www.21cnjy.com )周天历度.夫天不可阶而升,地不可得尺寸而度,请问数安从出?”商高答:“数之法出于圆方,圆出于方,方出于矩,矩出九九八十一,故折矩以为勾广三,股修四,径隅五.既方其外,半之一矩,环而共盘.得成三、四、五,两矩共长二十有五,是谓积矩.故禹之所以治天下者,此数之所由生也.”
(二)提出问题、建立模型、探索发现(15分钟)
提问:你听说过“勾股定理”吗?
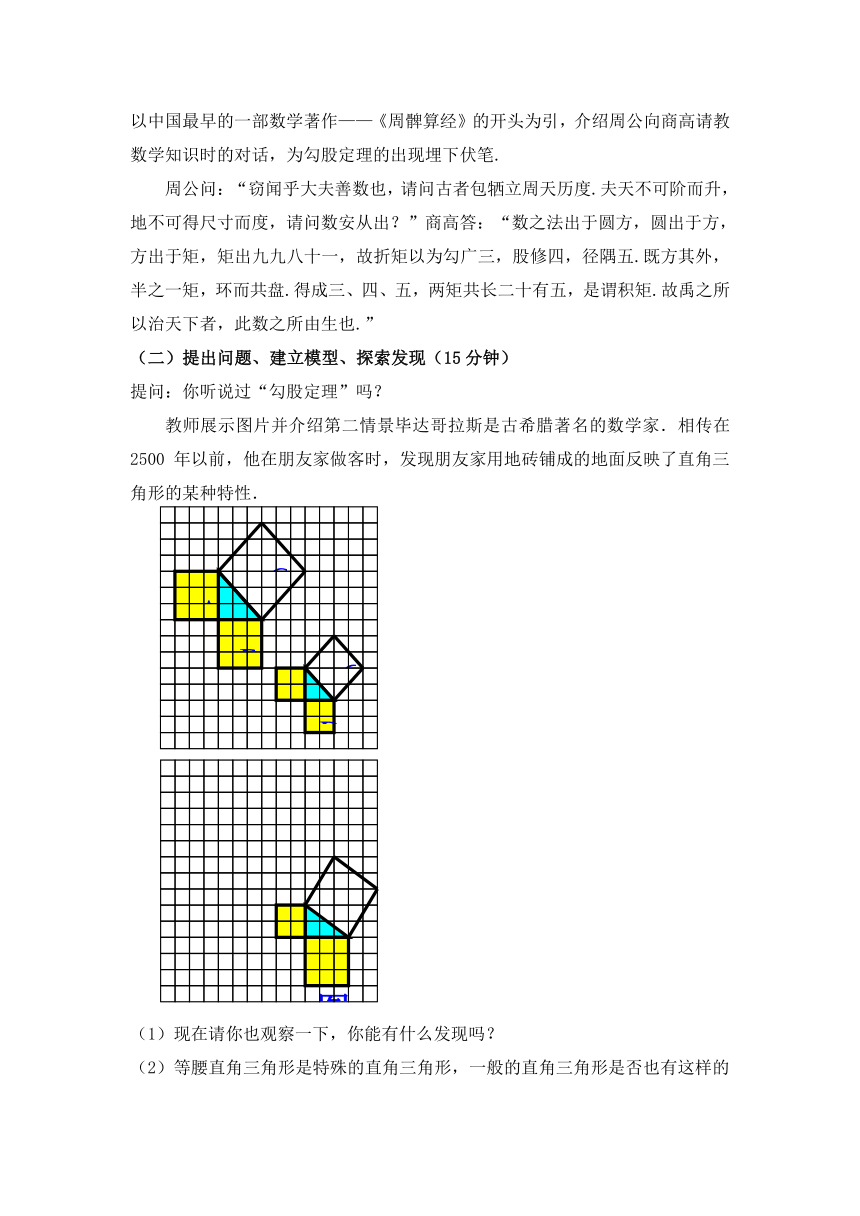
教师展示图片并介绍第二情景毕达哥拉斯是古希 ( http: / / www.21cnjy.com )腊著名的数学家.相传在2500年以前,他在朋友家做客时,发现朋友家用地砖铺成的地面反映了直角三角形的某种特性.
(1)现在请你也观察一下,你能有什么发现吗?
(2)等腰直角三角形是特殊的直角三角形,一般的直角三角形是否也有这样的特点呢?
(3)你们有新的结论吗?
教师总结:等腰直角三角形的两条直角边平方的和等于斜边的平方.(板书)
(三)得出新知,提炼规律(15分钟)
在独立探究的基础上,学生分组交流.教师参与小组活动,指导、倾听学生交流.针对不同认识水平的学生,引导其用不同的方法得出大正方形的面积.
教师多媒体展示:
2002年在北京召开了第2 ( http: / / www.21cnjy.com )4届国际数学家大会,它是最高水平的全球性数学科学学术会议,被誉为数学界的“奥运会”.这就是本届大会的会徽的图案.
提问:你见过这个图案吗?
( http: / / www.21cnjy.com )
教师作补充说明:这个图案是我国汉代数学 ( http: / / www.21cnjy.com )家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”是不是所有的直角三角形都有这样的特点呢?这就需要我们对一个一般的直角三角形进行证明.到目前为止,对这个命题的证明方法已有几百种之多.下面,我们就来看一看我国数学家赵爽是怎样证明这个命题的.
(1)以直角三角形ABC的两条直角边a、b为边作两个正方形.你能通过剪、拼把它拼成弦图的样子吗?
(2)面积分别怎样表示?它们有什么关系呢?
教师解释文言原话:「按弦图,又可勾 ( http: / / www.21cnjy.com )股相乘为朱实二,倍之为朱实四,以勾股之差相乘为中黄实,加差实,亦称弦实」.再用现在的数学符号,分别用a、b、c记勾、股、弦之长,赵爽所述即 2ab+(a-b)2=c2, 化简之得a2+b2=c2.
在直角三角形中,如果直角边分别为a和b,斜边为c,那么a2+b2=c2
(四)巩固运用、知识推广(7分钟)
随堂练习:
如图:一块长约80 m、宽约60 m的长方形草坪,被几个不自觉的学生沿对角线踏出了一条斜“路”,这种情况在生活中时有发生.
提问:
(1)这几位同学为什么不走正路,走斜“路”?
(2)他们知道走斜“路”比正路少走几步吗?
(3)他们这样做值得吗?
(五)课堂小结(3分钟)
通过本节课的学习,大家有什么收获?有什么疑问?你认为还有什么要继续探索的问题?
今天,我们学习 了勾股定理“直角三 ( http: / / www.21cnjy.com )角形的两直角边的平方和等于斜边的平方”.从几何上看,勾股定理是讲:以RtΔ 斜边为一边的正方形的面积等于分别以两直角边为边的正方形的面积之和.我国古代学者,就是用这种思路来证明勾股定理的.勾股定理反映了直角三角形三边之间的数量关系,因此是直角三角形的性质定理.
(六)作业布置(2分钟)
六、板书设计
17.1勾股定理(1)
1. 等腰直角三角形的两条直角边平方的和等于斜边的平方
2.在直角三角形中a2+b2=c2
B
C
A
B
C
C
图3-2
一、教材地位
本节课是人教版八年级下册第十七章第一节“ ( http: / / www.21cnjy.com )勾股定理”的第一课时.在本节课以前,学生已经学习了有关三角形的一些知识,也经历过利用图形面积来探求数式运算规律的过程。在探求勾股定理的过程中,蕴涵了丰富的数学思想.把三角形有一个直角“形”的特点转化为三边之间的“数”的关系,是数形结合的典范;把探求边的关系转化为探求面积的关系,将边不在格线上的图形转化为可计算的格点图形,是转化思想的体现;先探求特殊的直角三角形的三边关系,再探求一般直角三角形的三边关系,这是特殊——一般的思想.本节课,通过提供学生活动的方案,让学生在活动中思考,在思考中创新
二、教学目标
(一)知识与能力:
1.了解勾股定理的文化背景,体验勾股定理的探索过程
2.在勾股定理的探索过程中,发展合情推理能力,体会数形结合的思想
(二)过程与方法:
1.通过拼图活动,体验数学思维的严谨性,发展形象思维
2.在探究活动中,学会与人合作并能与他人交流思维的过程和探究结果
(三)情感态度价值观:
1.通过对勾股定理历史的了解,感受数学文化,激发学习热情
2.在探究活动中,体验解决问题方法的多样性,培养学生的合作交流意识和探索精神
三、教学重点与难点
重点:探索和证明勾股定理
难点:用拼图的方法证明勾股定理
四、课时安排及教具准备:一课时(45分钟)及一张卡片
五、 教学过程:
(一)引入新知、创设情境(2分钟)
以中国最早的一部数学著作——《周髀算经》的开头为引,介绍周公向商高请教数学知识时的对话,为勾股定理的出现埋下伏笔.
周公问:“窃闻乎大夫善数也,请问古者包牺立 ( http: / / www.21cnjy.com )周天历度.夫天不可阶而升,地不可得尺寸而度,请问数安从出?”商高答:“数之法出于圆方,圆出于方,方出于矩,矩出九九八十一,故折矩以为勾广三,股修四,径隅五.既方其外,半之一矩,环而共盘.得成三、四、五,两矩共长二十有五,是谓积矩.故禹之所以治天下者,此数之所由生也.”
(二)提出问题、建立模型、探索发现(15分钟)
提问:你听说过“勾股定理”吗?
教师展示图片并介绍第二情景毕达哥拉斯是古希 ( http: / / www.21cnjy.com )腊著名的数学家.相传在2500年以前,他在朋友家做客时,发现朋友家用地砖铺成的地面反映了直角三角形的某种特性.
(1)现在请你也观察一下,你能有什么发现吗?
(2)等腰直角三角形是特殊的直角三角形,一般的直角三角形是否也有这样的特点呢?
(3)你们有新的结论吗?
教师总结:等腰直角三角形的两条直角边平方的和等于斜边的平方.(板书)
(三)得出新知,提炼规律(15分钟)
在独立探究的基础上,学生分组交流.教师参与小组活动,指导、倾听学生交流.针对不同认识水平的学生,引导其用不同的方法得出大正方形的面积.
教师多媒体展示:
2002年在北京召开了第2 ( http: / / www.21cnjy.com )4届国际数学家大会,它是最高水平的全球性数学科学学术会议,被誉为数学界的“奥运会”.这就是本届大会的会徽的图案.
提问:你见过这个图案吗?
( http: / / www.21cnjy.com )
教师作补充说明:这个图案是我国汉代数学 ( http: / / www.21cnjy.com )家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”是不是所有的直角三角形都有这样的特点呢?这就需要我们对一个一般的直角三角形进行证明.到目前为止,对这个命题的证明方法已有几百种之多.下面,我们就来看一看我国数学家赵爽是怎样证明这个命题的.
(1)以直角三角形ABC的两条直角边a、b为边作两个正方形.你能通过剪、拼把它拼成弦图的样子吗?
(2)面积分别怎样表示?它们有什么关系呢?
教师解释文言原话:「按弦图,又可勾 ( http: / / www.21cnjy.com )股相乘为朱实二,倍之为朱实四,以勾股之差相乘为中黄实,加差实,亦称弦实」.再用现在的数学符号,分别用a、b、c记勾、股、弦之长,赵爽所述即 2ab+(a-b)2=c2, 化简之得a2+b2=c2.
在直角三角形中,如果直角边分别为a和b,斜边为c,那么a2+b2=c2
(四)巩固运用、知识推广(7分钟)
随堂练习:
如图:一块长约80 m、宽约60 m的长方形草坪,被几个不自觉的学生沿对角线踏出了一条斜“路”,这种情况在生活中时有发生.
提问:
(1)这几位同学为什么不走正路,走斜“路”?
(2)他们知道走斜“路”比正路少走几步吗?
(3)他们这样做值得吗?
(五)课堂小结(3分钟)
通过本节课的学习,大家有什么收获?有什么疑问?你认为还有什么要继续探索的问题?
今天,我们学习 了勾股定理“直角三 ( http: / / www.21cnjy.com )角形的两直角边的平方和等于斜边的平方”.从几何上看,勾股定理是讲:以RtΔ 斜边为一边的正方形的面积等于分别以两直角边为边的正方形的面积之和.我国古代学者,就是用这种思路来证明勾股定理的.勾股定理反映了直角三角形三边之间的数量关系,因此是直角三角形的性质定理.
(六)作业布置(2分钟)
六、板书设计
17.1勾股定理(1)
1. 等腰直角三角形的两条直角边平方的和等于斜边的平方
2.在直角三角形中a2+b2=c2
B
C
A
B
C
C
图3-2
