18.5 实践与探索 [下学期]
图片预览





文档简介
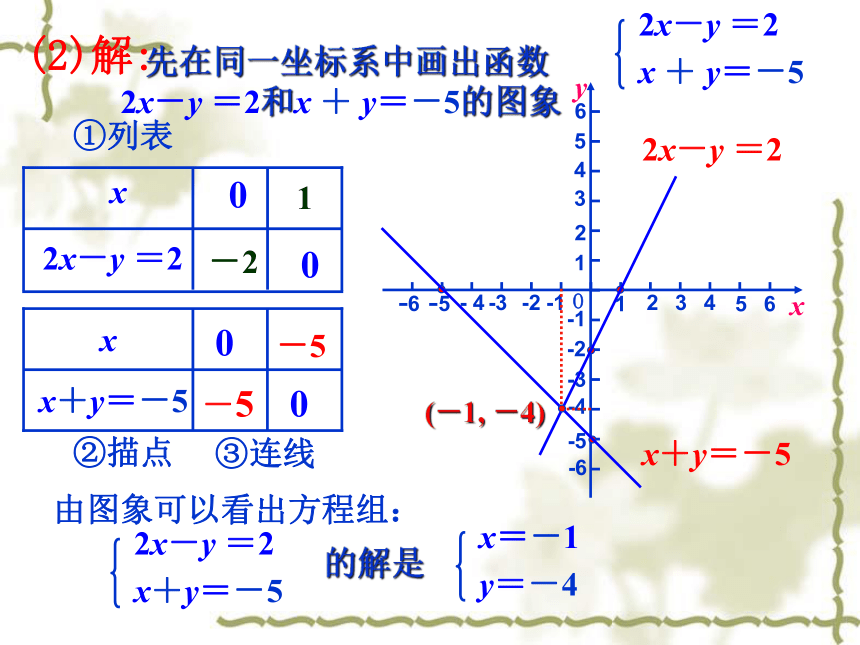
课件13张PPT。18.5.2实践与探索(1)(2)利用图象解方程组:情境导入 由上节课我们知道,两个一次函数图象的交点处,自变量和对应的函数值同时满足两个函数的关系式.而两个一次函数的关系式就是方程组中的两个方程,所以交点的坐标就是方程组的解. 据此,我们可以利用图象来求某些方程组的解以及不等式的解集.(1)解:①列表②描点③连线1-51 y=2x-5y= -x+1(2, -1) 先在同一坐标系中画出函数 y=2x-5和y=-x+1的图象由图象可以看出方程组:的解是y=-1x=2(2)解:①列表②描点③连线-5-2-5 2x-y =2x+y=-5(-1, -4) 先在同一坐标系中画出函数2x-y =2和x + y=-5的图象由图象可以看出方程组:的解是y=-4x=-111.二元一次方程与一次函数的关系
(1)以一个二元一次方程的任意一个解为坐标的点,它一定在这个一次函数的图象上; (2)一个一次函数图象上的任意一个点,它的坐标一定能适合某一个方程.
2.二元一次方程组的解与一次函数图象交点的关系
(1)一般地,以一个二元一次方程组的解为坐标的点,可以看作两个一次函数所组成的图象的交点(即是两条直线的交点).
(2)两个一次函数的所组成的图象的交点(即两条直线的交点),可以看成是某个二元一次方程组的解.小结画出函数 的图象,
根据图象,指出:
(1)x取什么值时,函数值y等于零?
(2)x取什么值时,函数值y始终大于零?探究并思考思 考 观察下图.
对照图象,请回答下列问题:
(1)当x取何值时,
2x-5=-x+1?
(2)当x取何值时,
2x-5>-x+1?
(3)当x取何值时,
2x-5<-x+1? y=2x-5y= -x+1(2, -1)例1 画出函数y=-x-2的图象,根据图象,指出:
(1) x取什么值时,函数值 y等于零?
(2) x取什么值时,函数值 y始终大于零?解:(1)当x=-2时,y=0;实践运用(2)当x<-2时,y>0.y=-x-2过点(0, -2) ,(-2,0) 作直线,如图.令x= 0,得y=-2 ;令 y =0,得x =-2 .例2 利用图象解不等式:
(1)2x-5>-x+1; (2) 2x-5<-x+1.解:在直角坐标系中画出这两条直线,如图.两条直线的交点坐标是(2, -1) ,可知:设y1=2x-5,y2=-x+1,(1)2x-5>-x+1的解集是y1>y2时,
x的取值范围,为x>-2;(2)2x-5<-x+1的解集是y1<y2时
x的取值范围,为x<-2. y=2x-5y=-x+1(2, -1)实践运用1.已知函数y=4x-3.当x取何值时,函数的
图象在第四象限?
2.画出函数y=3x-6的图象,根据图象,指出:
(1) x取什么值时,函数值 y等于零?
(2) x取什么值时,函数值 y大于零?
(3) x取什么值时,函数值 y小于零?反馈练习3.画出函数y=-0.5x-1的图象,根据图象,求:
(1)函数图象与x轴的交点坐标;
(2)函数图象在x轴上方时,x的取值范围;
(3)函数图象在x轴下方时,x的取值范围.反馈练习4.如图,一次函数y=kx+b的图象与反比例函数的图象交于A、B两点.(1)利用图中条件,求反比例
函数和一次函数的解析式;
(2)根据图象写出一次函数的
值大于反比例函数的值的x
的取值范围. 反馈练习小结 一次函数y=kx+b与x轴交点的横坐标是方程kx+b = 0的解.x轴上方的图象上的点的横坐标的集合是不等式kx+b> 0的解集;x轴下方的图象上的点的横坐标的集合是不等式kx+b <0的解集.
(1)以一个二元一次方程的任意一个解为坐标的点,它一定在这个一次函数的图象上; (2)一个一次函数图象上的任意一个点,它的坐标一定能适合某一个方程.
2.二元一次方程组的解与一次函数图象交点的关系
(1)一般地,以一个二元一次方程组的解为坐标的点,可以看作两个一次函数所组成的图象的交点(即是两条直线的交点).
(2)两个一次函数的所组成的图象的交点(即两条直线的交点),可以看成是某个二元一次方程组的解.小结画出函数 的图象,
根据图象,指出:
(1)x取什么值时,函数值y等于零?
(2)x取什么值时,函数值y始终大于零?探究并思考思 考 观察下图.
对照图象,请回答下列问题:
(1)当x取何值时,
2x-5=-x+1?
(2)当x取何值时,
2x-5>-x+1?
(3)当x取何值时,
2x-5<-x+1? y=2x-5y= -x+1(2, -1)例1 画出函数y=-x-2的图象,根据图象,指出:
(1) x取什么值时,函数值 y等于零?
(2) x取什么值时,函数值 y始终大于零?解:(1)当x=-2时,y=0;实践运用(2)当x<-2时,y>0.y=-x-2过点(0, -2) ,(-2,0) 作直线,如图.令x= 0,得y=-2 ;令 y =0,得x =-2 .例2 利用图象解不等式:
(1)2x-5>-x+1; (2) 2x-5<-x+1.解:在直角坐标系中画出这两条直线,如图.两条直线的交点坐标是(2, -1) ,可知:设y1=2x-5,y2=-x+1,(1)2x-5>-x+1的解集是y1>y2时,
x的取值范围,为x>-2;(2)2x-5<-x+1的解集是y1<y2时
x的取值范围,为x<-2. y=2x-5y=-x+1(2, -1)实践运用1.已知函数y=4x-3.当x取何值时,函数的
图象在第四象限?
2.画出函数y=3x-6的图象,根据图象,指出:
(1) x取什么值时,函数值 y等于零?
(2) x取什么值时,函数值 y大于零?
(3) x取什么值时,函数值 y小于零?反馈练习3.画出函数y=-0.5x-1的图象,根据图象,求:
(1)函数图象与x轴的交点坐标;
(2)函数图象在x轴上方时,x的取值范围;
(3)函数图象在x轴下方时,x的取值范围.反馈练习4.如图,一次函数y=kx+b的图象与反比例函数的图象交于A、B两点.(1)利用图中条件,求反比例
函数和一次函数的解析式;
(2)根据图象写出一次函数的
值大于反比例函数的值的x
的取值范围. 反馈练习小结 一次函数y=kx+b与x轴交点的横坐标是方程kx+b = 0的解.x轴上方的图象上的点的横坐标的集合是不等式kx+b> 0的解集;x轴下方的图象上的点的横坐标的集合是不等式kx+b <0的解集.
