2022--2023学年人教版八年级数学下册 18.1.2平行四边形的判定课后巩固练习(含答案)
文档属性
| 名称 | 2022--2023学年人教版八年级数学下册 18.1.2平行四边形的判定课后巩固练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 499.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-02 07:25:26 | ||
图片预览



文档简介
18.1.2平行四边形的判定课后巩固练习
一、单选题
1.如图,为了测量一块不规则绿地,两点间的距离,可以在绿地的一侧选定一点,然后测量出,的中点,,如果测量出,两点间的距离是,那么绿地,两点间的距离是( )
A. B. C. D.
2.下面给出四边形ABCD中∠A、∠B、∠C、∠D的度数之比,其中能判定四边形ABCD是平行四边形的是( )
A.3:4:4:3 B.2:2:3:3 C.4:3:2:1 D.4:3:4:3
3.如图所示,已知四边形ABCD,R、P分别是DC、BC上的点,点E、F分别是AP、RP的中点,当点P在边BC上从点B向点C移动,且点R从点D向点C移动时,那么下列结论成立的是( )
A.线段EF的长逐渐增大
B.线段EF的长逐渐减少
C.线段EF的长不变
D.△ABP和△CRP的面积和不变
4.在四边形中,,分别添加下列条件:①;,其中能使四边形成为平行四边形的条件有( )
A.5个 B.4个 C.3个 D.2个
5.如图,在ABC中,AB=13,BC=12,D、E分别是AB、BC的中点,连接DE,CD,如果DE=2.5,那么△ACD的周长为( )
A.25 B.18.5 C.17.5 D.18
6.如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,如果△ABC的周长为20,那么△DEF的周长是( )
A.20 B.15 C.10 D.5
7.如图,在中,,,,则的长为( )
A.6 B. C.12 D.
8.如图,平行四边形ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=,则AB的长是( )
A.0.5 B.1 C.1.5 D.2
9.如图,在中,,分别是、的中点,点在的延长线上.添加一个条件使四边形为平行四边形,则这个条件是( )
A. B. C. D.
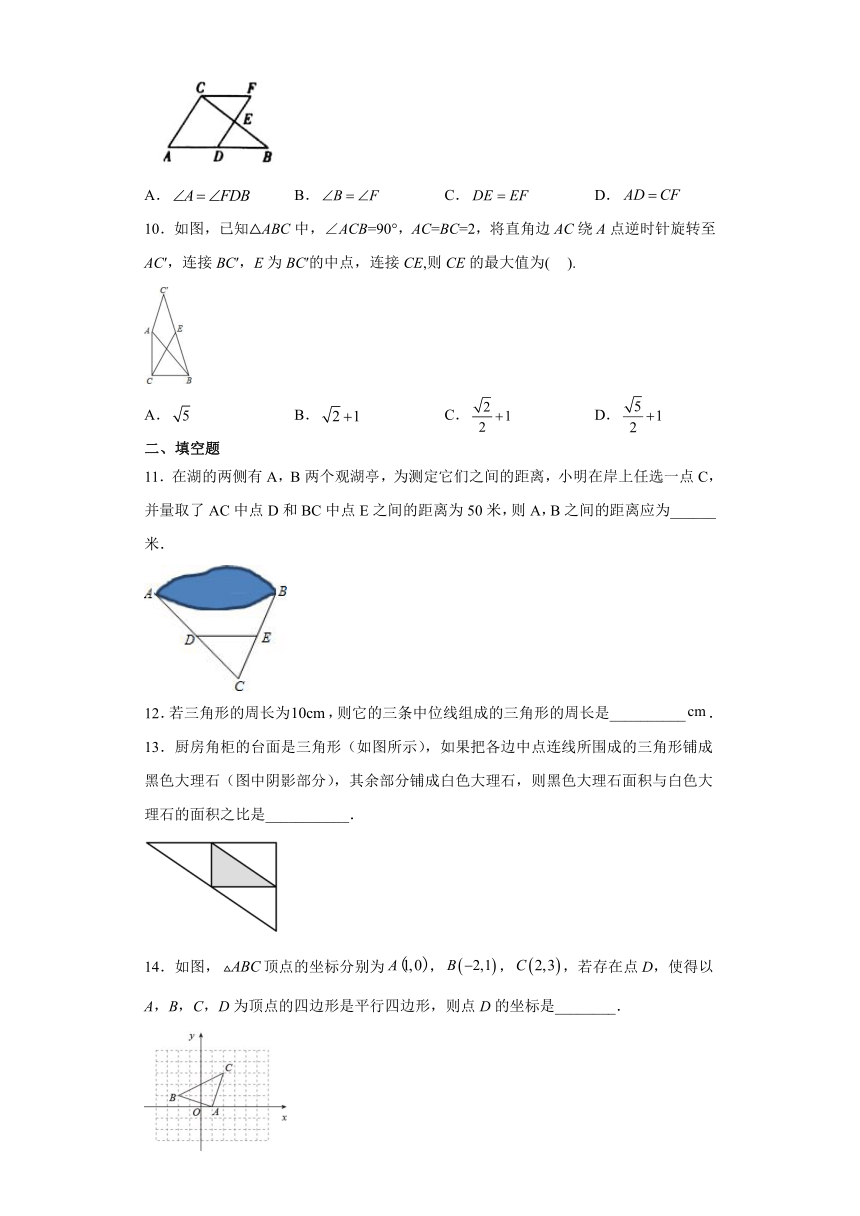
10.如图,已知△ABC中,∠ACB=90°,AC=BC=2,将直角边AC绕A点逆时针旋转至AC′,连接BC′,E为BC′的中点,连接CE,则CE的最大值为( ).
A. B. C. D.
二、填空题
11.在湖的两侧有A,B两个观湖亭,为测定它们之间的距离,小明在岸上任选一点C,并量取了AC中点D和BC中点E之间的距离为50米,则A,B之间的距离应为______米.
12.若三角形的周长为,则它的三条中位线组成的三角形的周长是__________.
13.厨房角柜的台面是三角形(如图所示),如果把各边中点连线所围成的三角形铺成黑色大理石(图中阴影部分),其余部分铺成白色大理石,则黑色大理石面积与白色大理石的面积之比是___________.
14.如图,顶点的坐标分别为,,,若存在点D,使得以A,B,C,D为顶点的四边形是平行四边形,则点D的坐标是________.
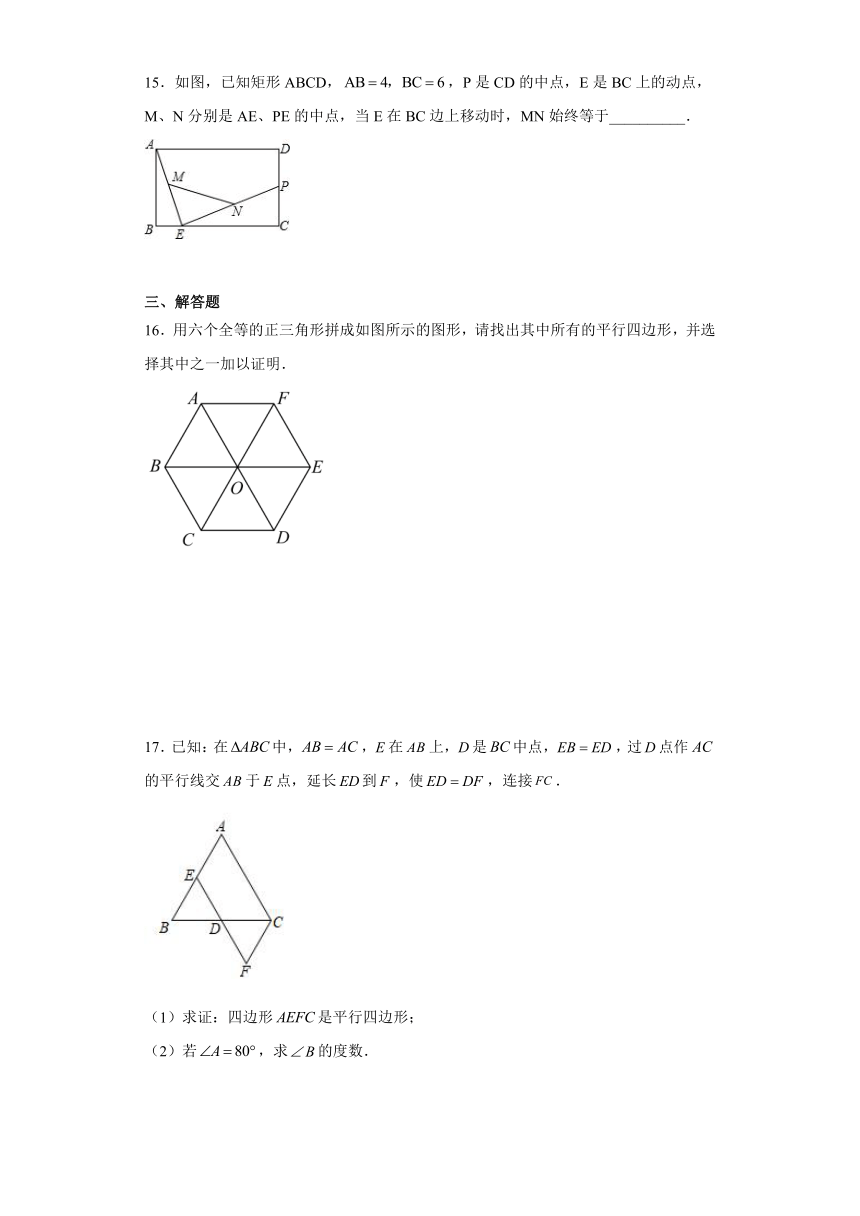
15.如图,已知矩形ABCD,,P是CD的中点,E是BC上的动点,M、N分别是AE、PE的中点,当E在BC边上移动时,MN始终等于__________.
三、解答题
16.用六个全等的正三角形拼成如图所示的图形,请找出其中所有的平行四边形,并选择其中之一加以证明.
17.已知:在中,,在上,是中点,,过点作的平行线交于点,延长到,使,连接.
(1)求证:四边形是平行四边形;
(2)若,求的度数.
18.如图,在 ABCD中,点E,F分别在边BC,AD上,且AF=CE.
求证:四边形AECF是平行四边形.
19.如图,已知在四边形中,,是对角线上的两点.,,.
(1)求证:;
(2)四边形是平行四边形吗?请说明理由.
20.已知,在平行四边形ABCD中,E为AD上一点,且AB=AE,连接BE交AC于点H,过点A作AF⊥BC于F,交BE于点G.
(1)若∠D=50°,求∠EBC的度数;
(2)若AC⊥CD,过点G作GM∥BC交AC于点M,求证:AH=MC.
参考答案
1.C
2.D
3.A
4.B
5.D
6.C
7.D
8.B
9.C
10.B
11.100
12.5
13./
14.,,
15.
16.解:所有的平行四边形为:,
根据题意得: ,
所以四边形 是平行四边形,
同理:四边形 是平行四边形.
17.证明:证明:是边的中点,
,
在和中,
,
,
,
,
,
四边形是平行四边形.
(2),
是等腰三角形,
,
且,
,
.
18.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∵AF=CE,
∴四边形AECF是平行四边形.
19.(1)证明:∵
∴
又∵
∴
∴
在和中
∴
(2)四边形是平行四边形.理由如下:
由(1)得
∴,∠DAF=∠BCE
∴AD∥BC
∴
∴四边形是平行四边形.
20.(1)∵AB=AE,
∴∠1=∠3,
∵AE∥BC,
∴∠2=∠3,
∴∠1=∠2=∠ABC,
又∵平行四边形ABCD中,∠D=50°,
∴∠ABC=50°,
∴∠EBC=25°;
(2)证明:如图,过M作MN⊥BC于N,过G作GP⊥AB于P,则∠CNM=∠APG=90°,
由(1)可得,∠1=∠2,
∵AF⊥BC,
∴∠BPG=∠BFG=90°,
在△BPG和△BFG中,
,
∴△BPG≌△BFG(AAS),
∴PG=GF,
又∵矩形GFNM中,GF=MN,
∴PG=NM,
∵AC⊥CD,CD∥AB,
∴∠BAC=90°=∠AFB,
即∠PAG+∠ABF=∠NCM+∠ABC=90°,
∴∠PAG=∠NCM,
在△PAG和△NCM中,
,
∴△PAG≌△NCM(AAS),
∴AG=CM,
∵∠1=∠2,∠BAH=∠BFG,
∴∠AHG=∠FGB=∠AGH,
∴AG=AH,
∴AH=CM.
一、单选题
1.如图,为了测量一块不规则绿地,两点间的距离,可以在绿地的一侧选定一点,然后测量出,的中点,,如果测量出,两点间的距离是,那么绿地,两点间的距离是( )
A. B. C. D.
2.下面给出四边形ABCD中∠A、∠B、∠C、∠D的度数之比,其中能判定四边形ABCD是平行四边形的是( )
A.3:4:4:3 B.2:2:3:3 C.4:3:2:1 D.4:3:4:3
3.如图所示,已知四边形ABCD,R、P分别是DC、BC上的点,点E、F分别是AP、RP的中点,当点P在边BC上从点B向点C移动,且点R从点D向点C移动时,那么下列结论成立的是( )
A.线段EF的长逐渐增大
B.线段EF的长逐渐减少
C.线段EF的长不变
D.△ABP和△CRP的面积和不变
4.在四边形中,,分别添加下列条件:①;,其中能使四边形成为平行四边形的条件有( )
A.5个 B.4个 C.3个 D.2个
5.如图,在ABC中,AB=13,BC=12,D、E分别是AB、BC的中点,连接DE,CD,如果DE=2.5,那么△ACD的周长为( )
A.25 B.18.5 C.17.5 D.18
6.如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,如果△ABC的周长为20,那么△DEF的周长是( )
A.20 B.15 C.10 D.5
7.如图,在中,,,,则的长为( )
A.6 B. C.12 D.
8.如图,平行四边形ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=,则AB的长是( )
A.0.5 B.1 C.1.5 D.2
9.如图,在中,,分别是、的中点,点在的延长线上.添加一个条件使四边形为平行四边形,则这个条件是( )
A. B. C. D.
10.如图,已知△ABC中,∠ACB=90°,AC=BC=2,将直角边AC绕A点逆时针旋转至AC′,连接BC′,E为BC′的中点,连接CE,则CE的最大值为( ).
A. B. C. D.
二、填空题
11.在湖的两侧有A,B两个观湖亭,为测定它们之间的距离,小明在岸上任选一点C,并量取了AC中点D和BC中点E之间的距离为50米,则A,B之间的距离应为______米.
12.若三角形的周长为,则它的三条中位线组成的三角形的周长是__________.
13.厨房角柜的台面是三角形(如图所示),如果把各边中点连线所围成的三角形铺成黑色大理石(图中阴影部分),其余部分铺成白色大理石,则黑色大理石面积与白色大理石的面积之比是___________.
14.如图,顶点的坐标分别为,,,若存在点D,使得以A,B,C,D为顶点的四边形是平行四边形,则点D的坐标是________.
15.如图,已知矩形ABCD,,P是CD的中点,E是BC上的动点,M、N分别是AE、PE的中点,当E在BC边上移动时,MN始终等于__________.
三、解答题
16.用六个全等的正三角形拼成如图所示的图形,请找出其中所有的平行四边形,并选择其中之一加以证明.
17.已知:在中,,在上,是中点,,过点作的平行线交于点,延长到,使,连接.
(1)求证:四边形是平行四边形;
(2)若,求的度数.
18.如图,在 ABCD中,点E,F分别在边BC,AD上,且AF=CE.
求证:四边形AECF是平行四边形.
19.如图,已知在四边形中,,是对角线上的两点.,,.
(1)求证:;
(2)四边形是平行四边形吗?请说明理由.
20.已知,在平行四边形ABCD中,E为AD上一点,且AB=AE,连接BE交AC于点H,过点A作AF⊥BC于F,交BE于点G.
(1)若∠D=50°,求∠EBC的度数;
(2)若AC⊥CD,过点G作GM∥BC交AC于点M,求证:AH=MC.
参考答案
1.C
2.D
3.A
4.B
5.D
6.C
7.D
8.B
9.C
10.B
11.100
12.5
13./
14.,,
15.
16.解:所有的平行四边形为:,
根据题意得: ,
所以四边形 是平行四边形,
同理:四边形 是平行四边形.
17.证明:证明:是边的中点,
,
在和中,
,
,
,
,
,
四边形是平行四边形.
(2),
是等腰三角形,
,
且,
,
.
18.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∵AF=CE,
∴四边形AECF是平行四边形.
19.(1)证明:∵
∴
又∵
∴
∴
在和中
∴
(2)四边形是平行四边形.理由如下:
由(1)得
∴,∠DAF=∠BCE
∴AD∥BC
∴
∴四边形是平行四边形.
20.(1)∵AB=AE,
∴∠1=∠3,
∵AE∥BC,
∴∠2=∠3,
∴∠1=∠2=∠ABC,
又∵平行四边形ABCD中,∠D=50°,
∴∠ABC=50°,
∴∠EBC=25°;
(2)证明:如图,过M作MN⊥BC于N,过G作GP⊥AB于P,则∠CNM=∠APG=90°,
由(1)可得,∠1=∠2,
∵AF⊥BC,
∴∠BPG=∠BFG=90°,
在△BPG和△BFG中,
,
∴△BPG≌△BFG(AAS),
∴PG=GF,
又∵矩形GFNM中,GF=MN,
∴PG=NM,
∵AC⊥CD,CD∥AB,
∴∠BAC=90°=∠AFB,
即∠PAG+∠ABF=∠NCM+∠ABC=90°,
∴∠PAG=∠NCM,
在△PAG和△NCM中,
,
∴△PAG≌△NCM(AAS),
∴AG=CM,
∵∠1=∠2,∠BAH=∠BFG,
∴∠AHG=∠FGB=∠AGH,
∴AG=AH,
∴AH=CM.
