19.2 一次函数与一元一次方程教案
文档属性
| 名称 | 19.2 一次函数与一元一次方程教案 |  | |
| 格式 | zip | ||
| 文件大小 | 56.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-06-22 16:25:36 | ||
图片预览

文档简介
课 题 一次函数与一元一次方程 课型 自主探究课 班级 7班
执教单位 会东中学 姓名 徐老师 时间 2014.5.20
学习目标 知识目标:1.理解一次函数与一元一次方程的关系.2.会根据一次函数的图象解决一元一次方程的求解的相关问题.能力目标:经历探索一元一次方程与一次函数的内在联系,体会数与形结合的数学思想.情感目标:1.通过对一次函数与一元一次方程关系的探索,培养学生严谨的科学态度及勇于探索的精神.2.通过从函数的角度看问题,让学生体会数学的价值.
学习重点 一次函数与一元一次方程关系的理解.
学习难点 一次函数与一元一次方程在“形”上的关系.
学前准备 布置预习任务,填写预习单.
课堂流程 具体内容 学法指导
一创设情境提出目标 华罗庚,国际数学大师,他为中国数学的发 ( http: / / www.21cnjy.com )展作出了无与伦比的贡献,被誉为“中国现代数学之父”.他在谈到数形结合的好处时曾作诗赞美: 数缺形时少直观,形少数时难入微.数形结合百般好,隔离分家万事休.我们来看下面两个问题:1.解方程.2.当自变量为何值时,函数的值为0?这两个问题之间有什么联系吗?我们这节课就来研究它们之间的关系,并学习用这种关系解决相关问题的方法.这节课我们的学习目标是:从数和形两个角度理解一次函数与一元一次方程的关系.会根据一次函数的图象解决一元一次方程的求解的相关问题. 用心体会数形结合的思想在数学解题中的应用. 新旧知识联系,明确学习目标,带着问题学习.
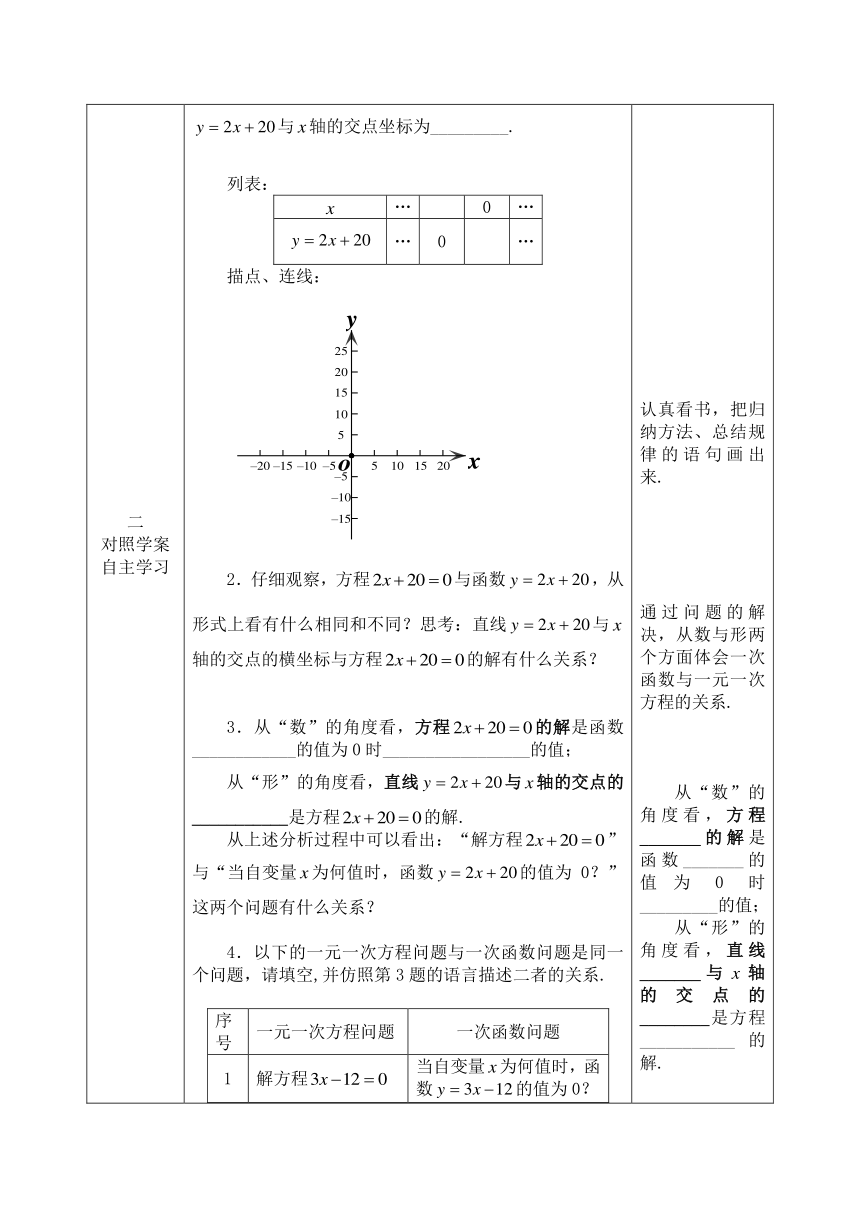
二对照学案自主学习二对照学案自主学习 (一)阅读教材第123页的内容,完成下列问题:1.①方程的解为___________;②若函数的值为0,则自变量=______.③画出一次函数的图象,观察图象,直线与轴的交点坐标为_________.列表:…0……0…描点、连线: ( http: / / www.21cnjy.com )2.仔细观察,方程与函数,从形式上看有什么相同和不同?思考:直线与轴的交点的横坐标与方程的解有什么关系? 3.从“数”的角度看,方程的解是函数____________的值为0时_________________的值;从“形”的角度看,直线与轴的交点的___________是方程的解.从上述分析过程中可以看出:“解方程”与“当自变量为何值时,函数的值为0?”这两个问题有什么关系?4.以下的一元一次方程问题与一次函数问题是同一个问题,请填空,并仿照第3题的语言描述二者的关系.序号一元一次方程问题一次函数问题1解方程当自变量为何值时,函数的值为0?2当自变量为何值时,函数的值为0?3解方程(为常数,≠0)5.试着将下列方程转化为(为常数,≠0)的形式.(1); (2). 6.由上面练习可知,任何一个一元一次方程都可转化为___________________________的形式;对于一次函数,当函数值为0时,即__________=0,就与一元一次方程的形式完全相同.所以解一元一次方程可以转化为:当某个一次函数的值为0时,求相应的自变量的值.从图象上看,这相当于已知直线__________,确定它与轴交点的___________的值.换言之,方程(为常数,≠0)的解是函数______________的值为0时_________________的值;直线____________与轴交点的__________是方程(为常数,≠0)的解.(二)阅读教材第124页例1,探究下列问题:1.解法1是构建了什么模型解决问题的?2.在解法2中,求再过几秒它的速度为17米/秒,实际上就是求函数关系式__________中,等于___时,自变量的值?3.为什么要画出函数的图象?从图象如何得到问题的结果?我们能否通过画出函数的图象,观察图象解决问题?4.解法1与解法2相比,二者分别从什么方面得出结果的?(三)利用图象求方程的解. ( http: / / www.21cnjy.com ) 认真看书,把归纳方法、总结规律的语句画出来.通过问题的解决,从数与形两个方面体会一次函数与一元一次方程的关系.从“数”的角度看,方程_______的解是函数_______的值为0时_________的值;从“形”的角度看,直线_______与轴的交点的________是方程___________的解.用函数的观点从数和形两个角度对解一元一次方程进行描述.明确教材中例题的解题依据、思路及方法.规范解法,完善思路.体会图象法解方程的优缺点.
三梳理问题合作交流 每位同学针对自学中存在的问题、困惑,在组内 ( http: / / www.21cnjy.com )展开交流,共享本组的收获,小组长要组织好本组的讨论,将本组解决不了的疑难问题整理出来,告诉老师,然后组间交流. 同伴间要相互合作,积极讨论交流,补充完善,解决问题.
四展示成果师生点评 分组依次展示小组讨论中的难点问题,本节课的重点问题. 展示时对重点内容要用色粉笔突出显示,其他同学认真倾听,不完整的加以补充.
五总结深化拓展提高 请从以下几方面谈谈你的体会和收获.【知识】:______________________________________【方法】:______________________________________【困惑】:______________________________________【教师总结】【布置作业】1、习题14.3第1、2题2、导学案第118页第1——7题. 【自我检测题】1.方程的解是__________,则直线与轴的交点的横坐标是_______. 2.若直线与轴交于点(-3,0),则方程的解是=____.3.已知关于的方程的解是,则直线与轴的交点坐标是________.4.一次函数的图象如图所示,则一元一次方程的解是=_____. 通过小结,明确本节的内容,思想和方法,养成善于反思的学习习惯.强化识图能力,提高图形、图象信息分析能力,从数和形两个角度理解一次函数与一元一次方程的关系.
HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" (第4题图) (第5题图)5.如图,是一次函数的图象,观察图象思考:当时,=________;当时,=________.由此可知方程的解是_________,方程的解是_________.
教学反思 本节课创设情境,调动学生学习的积极性,提出 ( http: / / www.21cnjy.com )学习目标,以问题为载体引领学生对新知展开探究、交流与讨论,并让学生以小组展示学习成果,突出了“学生为主体,教师为主导”的教学理念,让学生真正成为课堂学习的主人.
执教单位 会东中学 姓名 徐老师 时间 2014.5.20
学习目标 知识目标:1.理解一次函数与一元一次方程的关系.2.会根据一次函数的图象解决一元一次方程的求解的相关问题.能力目标:经历探索一元一次方程与一次函数的内在联系,体会数与形结合的数学思想.情感目标:1.通过对一次函数与一元一次方程关系的探索,培养学生严谨的科学态度及勇于探索的精神.2.通过从函数的角度看问题,让学生体会数学的价值.
学习重点 一次函数与一元一次方程关系的理解.
学习难点 一次函数与一元一次方程在“形”上的关系.
学前准备 布置预习任务,填写预习单.
课堂流程 具体内容 学法指导
一创设情境提出目标 华罗庚,国际数学大师,他为中国数学的发 ( http: / / www.21cnjy.com )展作出了无与伦比的贡献,被誉为“中国现代数学之父”.他在谈到数形结合的好处时曾作诗赞美: 数缺形时少直观,形少数时难入微.数形结合百般好,隔离分家万事休.我们来看下面两个问题:1.解方程.2.当自变量为何值时,函数的值为0?这两个问题之间有什么联系吗?我们这节课就来研究它们之间的关系,并学习用这种关系解决相关问题的方法.这节课我们的学习目标是:从数和形两个角度理解一次函数与一元一次方程的关系.会根据一次函数的图象解决一元一次方程的求解的相关问题. 用心体会数形结合的思想在数学解题中的应用. 新旧知识联系,明确学习目标,带着问题学习.
二对照学案自主学习二对照学案自主学习 (一)阅读教材第123页的内容,完成下列问题:1.①方程的解为___________;②若函数的值为0,则自变量=______.③画出一次函数的图象,观察图象,直线与轴的交点坐标为_________.列表:…0……0…描点、连线: ( http: / / www.21cnjy.com )2.仔细观察,方程与函数,从形式上看有什么相同和不同?思考:直线与轴的交点的横坐标与方程的解有什么关系? 3.从“数”的角度看,方程的解是函数____________的值为0时_________________的值;从“形”的角度看,直线与轴的交点的___________是方程的解.从上述分析过程中可以看出:“解方程”与“当自变量为何值时,函数的值为0?”这两个问题有什么关系?4.以下的一元一次方程问题与一次函数问题是同一个问题,请填空,并仿照第3题的语言描述二者的关系.序号一元一次方程问题一次函数问题1解方程当自变量为何值时,函数的值为0?2当自变量为何值时,函数的值为0?3解方程(为常数,≠0)5.试着将下列方程转化为(为常数,≠0)的形式.(1); (2). 6.由上面练习可知,任何一个一元一次方程都可转化为___________________________的形式;对于一次函数,当函数值为0时,即__________=0,就与一元一次方程的形式完全相同.所以解一元一次方程可以转化为:当某个一次函数的值为0时,求相应的自变量的值.从图象上看,这相当于已知直线__________,确定它与轴交点的___________的值.换言之,方程(为常数,≠0)的解是函数______________的值为0时_________________的值;直线____________与轴交点的__________是方程(为常数,≠0)的解.(二)阅读教材第124页例1,探究下列问题:1.解法1是构建了什么模型解决问题的?2.在解法2中,求再过几秒它的速度为17米/秒,实际上就是求函数关系式__________中,等于___时,自变量的值?3.为什么要画出函数的图象?从图象如何得到问题的结果?我们能否通过画出函数的图象,观察图象解决问题?4.解法1与解法2相比,二者分别从什么方面得出结果的?(三)利用图象求方程的解. ( http: / / www.21cnjy.com ) 认真看书,把归纳方法、总结规律的语句画出来.通过问题的解决,从数与形两个方面体会一次函数与一元一次方程的关系.从“数”的角度看,方程_______的解是函数_______的值为0时_________的值;从“形”的角度看,直线_______与轴的交点的________是方程___________的解.用函数的观点从数和形两个角度对解一元一次方程进行描述.明确教材中例题的解题依据、思路及方法.规范解法,完善思路.体会图象法解方程的优缺点.
三梳理问题合作交流 每位同学针对自学中存在的问题、困惑,在组内 ( http: / / www.21cnjy.com )展开交流,共享本组的收获,小组长要组织好本组的讨论,将本组解决不了的疑难问题整理出来,告诉老师,然后组间交流. 同伴间要相互合作,积极讨论交流,补充完善,解决问题.
四展示成果师生点评 分组依次展示小组讨论中的难点问题,本节课的重点问题. 展示时对重点内容要用色粉笔突出显示,其他同学认真倾听,不完整的加以补充.
五总结深化拓展提高 请从以下几方面谈谈你的体会和收获.【知识】:______________________________________【方法】:______________________________________【困惑】:______________________________________【教师总结】【布置作业】1、习题14.3第1、2题2、导学案第118页第1——7题. 【自我检测题】1.方程的解是__________,则直线与轴的交点的横坐标是_______. 2.若直线与轴交于点(-3,0),则方程的解是=____.3.已知关于的方程的解是,则直线与轴的交点坐标是________.4.一次函数的图象如图所示,则一元一次方程的解是=_____. 通过小结,明确本节的内容,思想和方法,养成善于反思的学习习惯.强化识图能力,提高图形、图象信息分析能力,从数和形两个角度理解一次函数与一元一次方程的关系.
HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" (第4题图) (第5题图)5.如图,是一次函数的图象,观察图象思考:当时,=________;当时,=________.由此可知方程的解是_________,方程的解是_________.
教学反思 本节课创设情境,调动学生学习的积极性,提出 ( http: / / www.21cnjy.com )学习目标,以问题为载体引领学生对新知展开探究、交流与讨论,并让学生以小组展示学习成果,突出了“学生为主体,教师为主导”的教学理念,让学生真正成为课堂学习的主人.
