人教版2023年中考数学模拟试卷(三)(含答案)
文档属性
| 名称 | 人教版2023年中考数学模拟试卷(三)(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 169.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-29 21:22:48 | ||
图片预览

文档简介
人教版2023年中考数学模拟试卷(三)
一、单选题
1.下列各命题中假命题的是( )
A.全等三角形的对应角相等 B.如果两个数相等,那么它们的绝对值相等
C.两直线平行,同位角相等 D.如果两个角相等,那么这两个角是对顶角
2.中国疫苗撑起全球抗疫“生命线”中国外交部数据显示,截止2021年3月底,我国已无偿向80个国家和3个国际组织提供疫苗援助.预计2022年中国新冠疫苗产能有望达到50亿剂,约占全球的一半,必将为全球抗疫作出重大贡献.数据“50亿”用科学记数法表示为( )
A. B. C. D.
3.下列说法中,正确的是( )
A.“射击运动员射击一次,命中靶心”是必然事件 B.不可能事件发生的概率为0
C.随机事件发生的概率为 D.投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次
4.a,b是有理数,它们在数轴上的对应点的位置如图所示,对于以下结论,正确的是( )
A. B. C. D.
5.如图,已知二次函数 的图像如图所示,有下列5个结论:① ,② ,③ ,④⑤ 。其中正确的结论有( )
A.①②③ B.①③ ④ C.③④⑤ D.②③⑤
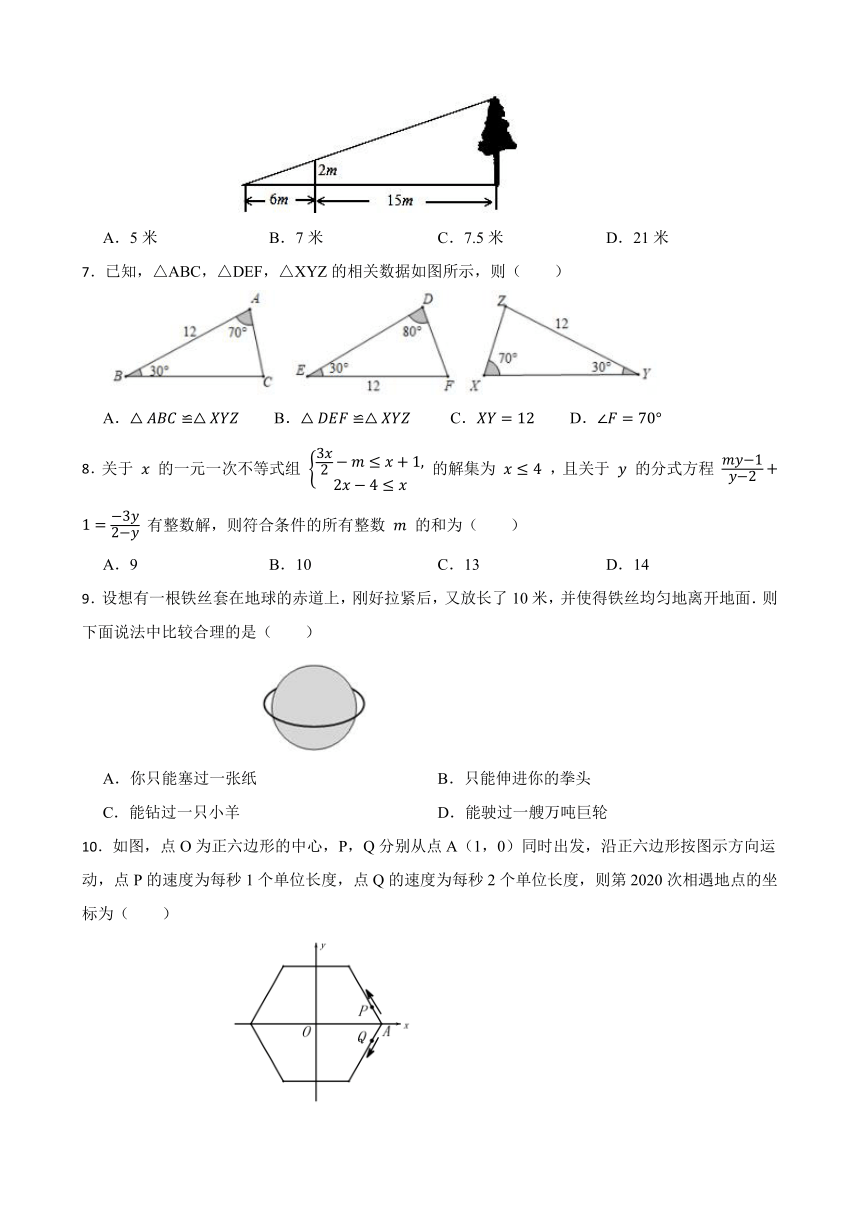
6.如图:为了测量某棵树的高度,小刚用长为2m的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点,此时,竹竿与这一点距离6m,与树相距15m,那么这棵的高度为( )
A.5米 B.7米 C.7.5米 D.21米
7.已知,△ABC,△DEF,△XYZ的相关数据如图所示,则( )
A.B. C.D.
8.关于 的一元一次不等式组 的解集为 ,且关于 的分式方程 有整数解,则符合条件的所有整数 的和为( )
A.9 B.10 C.13 D.14
9.设想有一根铁丝套在地球的赤道上,刚好拉紧后,又放长了10米,并使得铁丝均匀地离开地面.则下面说法中比较合理的是( )
A.你只能塞过一张纸 B.只能伸进你的拳头
C.能钻过一只小羊 D.能驶过一艘万吨巨轮
10.如图,点O为正六边形的中心,P,Q分别从点A(1,0)同时出发,沿正六边形按图示方向运动,点P的速度为每秒1个单位长度,点Q的速度为每秒2个单位长度,则第2020次相遇地点的坐标为( )
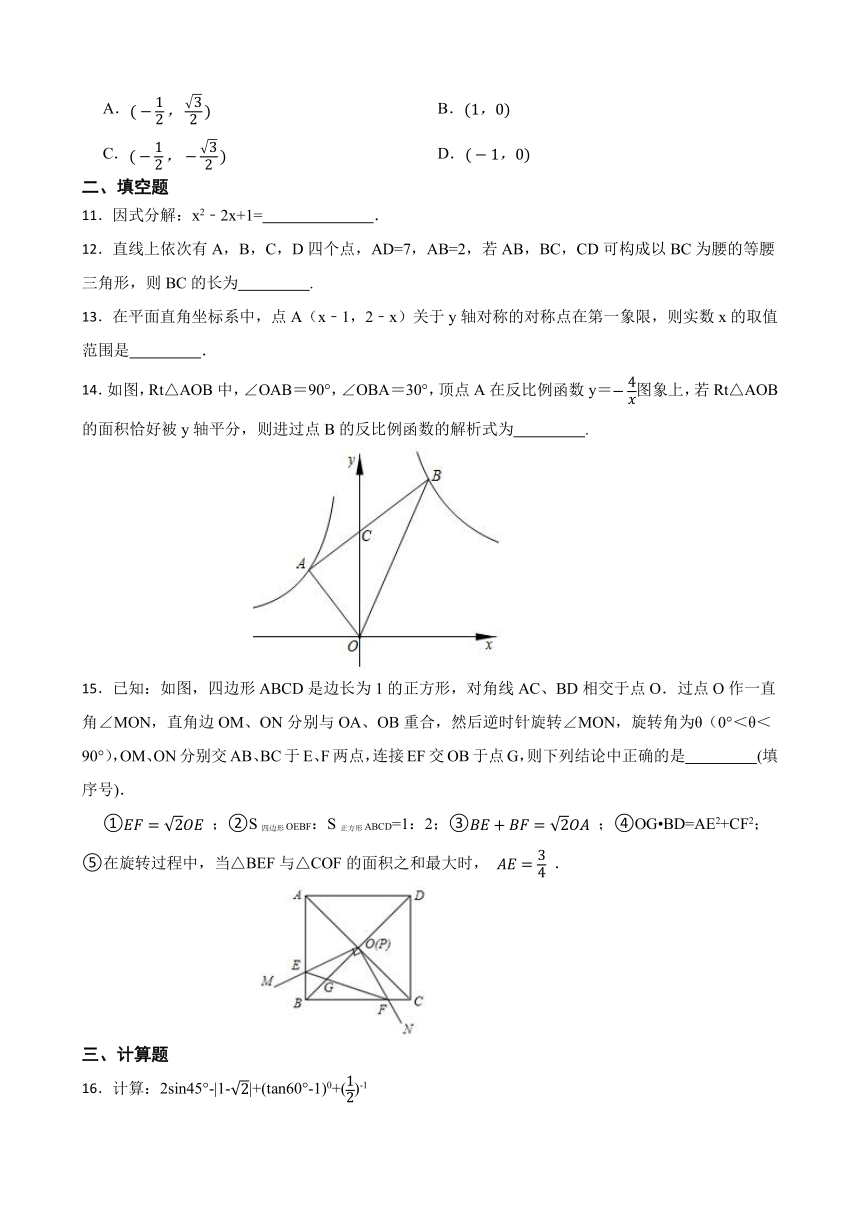
A. B.
C. D.
二、填空题
11.因式分解:x2﹣2x+1= .
12.直线上依次有A,B,C,D四个点,AD=7,AB=2,若AB,BC,CD可构成以BC为腰的等腰三角形,则BC的长为 .
13.在平面直角坐标系中,点A(x﹣1,2﹣x)关于y轴对称的对称点在第一象限,则实数x的取值范围是 .
14.如图,Rt△AOB中,∠OAB=90°,∠OBA=30°,顶点A在反比例函数y=图象上,若Rt△AOB的面积恰好被y轴平分,则进过点B的反比例函数的解析式为 .
15.已知:如图,四边形ABCD是边长为1的正方形,对角线AC、BD相交于点O.过点O作一直角∠MON,直角边OM、ON分别与OA、OB重合,然后逆时针旋转∠MON,旋转角为θ(0°<θ<90°),OM、ON分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是 (填序号).
① ;②S四边形OEBF:S正方形ABCD=1:2;③ ;④OG BD=AE2+CF2;⑤在旋转过程中,当△BEF与△COF的面积之和最大时, .
三、计算题
16.计算:2sin45°-|1-|+(tan60°-1)0+()-1
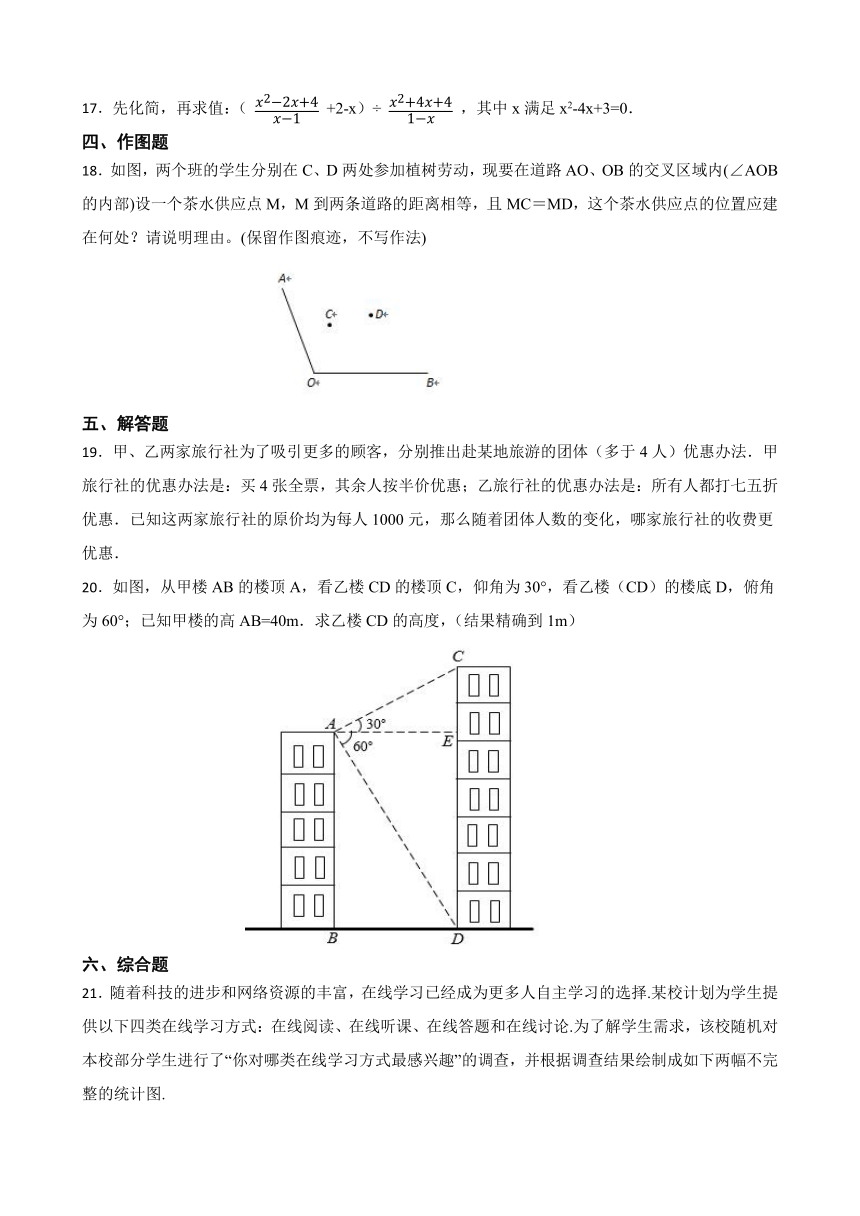
17.先化简,再求值:( +2-x)÷ ,其中x满足x2-4x+3=0.
四、作图题
18.如图,两个班的学生分别在C、D两处参加植树劳动,现要在道路AO、OB的交叉区域内(∠AOB的内部)设一个茶水供应点M,M到两条道路的距离相等,且MC=MD,这个茶水供应点的位置应建在何处?请说明理由。(保留作图痕迹,不写作法)
五、解答题
19.甲、乙两家旅行社为了吸引更多的顾客,分别推出赴某地旅游的团体(多于4人)优惠办法.甲旅行社的优惠办法是:买4张全票,其余人按半价优惠;乙旅行社的优惠办法是:所有人都打七五折优惠.已知这两家旅行社的原价均为每人1000元,那么随着团体人数的变化,哪家旅行社的收费更优惠.
20.如图,从甲楼AB的楼顶A,看乙楼CD的楼顶C,仰角为30°,看乙楼(CD)的楼底D,俯角为60°;已知甲楼的高AB=40m.求乙楼CD的高度,(结果精确到1m)
六、综合题
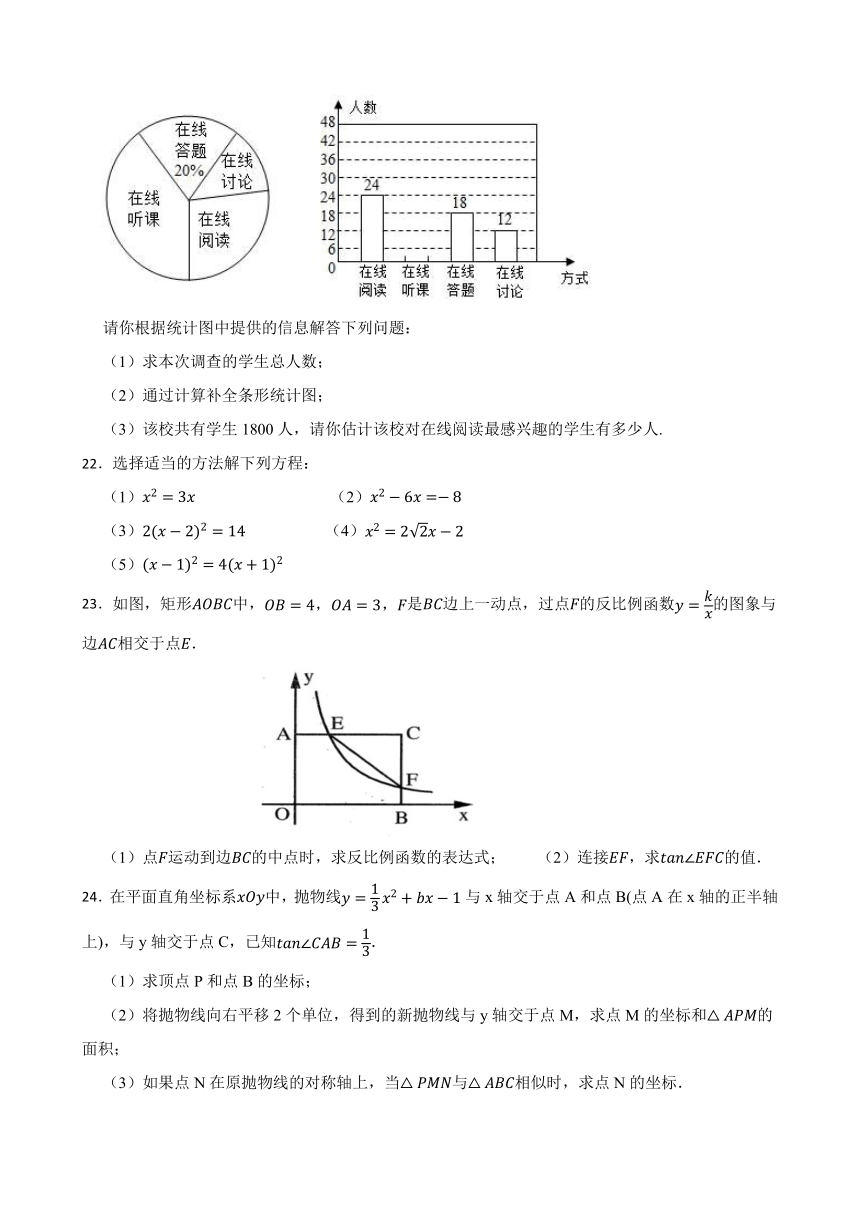
21.随着科技的进步和网络资源的丰富,在线学习已经成为更多人自主学习的选择.某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论.为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图.
请你根据统计图中提供的信息解答下列问题:
(1)求本次调查的学生总人数;
(2)通过计算补全条形统计图;
(3)该校共有学生1800人,请你估计该校对在线阅读最感兴趣的学生有多少人.
22.选择适当的方法解下列方程:
(1) (2)
(3) (4)
(5)
23.如图,矩形中,是边上一动点,过点的反比例函数的图象与边相交于点.
(1)点运动到边的中点时,求反比例函数的表达式; (2)连接,求的值.
24.在平面直角坐标系中,抛物线与x轴交于点A和点B(点A在x轴的正半轴上),与y轴交于点C,已知.
(1)求顶点P和点B的坐标;
(2)将抛物线向右平移2个单位,得到的新抛物线与y轴交于点M,求点M的坐标和的面积;
(3)如果点N在原抛物线的对称轴上,当与相似时,求点N的坐标.
答 案
1.D 2.C 3.B 4.B 5.B 6.A 7.D 8.A 9.C 10.A 11.(x﹣1)2
12.2或2.5 13.x<1 14.10 15.①③④
16.解:2sin45°-|1-|+(tan60°-1)0+()-1=2×+1-+1+2=4.
17.解:原式= ÷ = =- ,
解方程x2-4x+3=0得,
(x-1)(x-3)=0, x1=1,x2=3.
当x=1时,原式无意义;当x=3时,原式=- =- .
18.解:如图,
∠O的平分线和CD的垂直平分线的交点即为茶水供应点的位置.理由是:因为M是∠O的平分线和CD的垂直平分线的交点,所以M到∠O的两边OA和OB的距离相等,M到C、D的距离相等,所以M就是所求.
19.解:设团体有人,收费元
∴,
∵当时,,解得;
∴当时,,解得;
当时,,解得;
∴当团体人数超过8人时,选甲旅行社收费更优惠;
当团体人数为8人时,两家旅行社收费相同;
当团体人数少于8人时,选乙旅行社收费更优惠.
20.解:由题意得:∠AEC=∠AED=90°,AB=DE=40m,∠EAD=60°,∠CAE=30°,
∴, ∴,
∴,
即乙楼CD的高度为53m.
21.(1)解:本次调查的学生总人数为 (人)
∴本次调查的学生总人数为90人;
(2)解:在线听课的人数为: (人)
∴在线听课的人数为36人;
补全的条形统计图如图所示
(3)解: (人)
答:估计该校对在线阅读最感兴趣的学生有480人.
22.(1)解:,移项得:,
提取公因式得:,,,
,;
(2)解:,移项得:,
因式分解得:,
,,,;
(3)解:,
系数化为1得:,
开平方得:,
,,
,;
(4)解:
移项得:,
因式分解得:,
,
;
(5)解:,
移项得:,
去括号得:,
化简得:,
因式分解得:,
,,
,.
23.(1)解:是的中点,
,
点的坐标为,
将点的坐标为代入得:
∴,
∴反比例函数的表达式;
(2)解:点的横坐标为4,代入,
, ,
,
点的纵坐标为3,代入,
,即,,,
所以.
24.(1)解:根据题意可画出函数图象,如图1,
令可得,
∴,即.
在中,,
∴, ∴, ∴.
将点A的坐标代入抛物线解析式可得,,
解得.
∴抛物线的解析式为:.
∴顶点,
令,即,
∴或,
∴.
(2)解:如图2,
将(1)中抛物线向右平移2个单位,得到的新抛物线.
令,则.
∴
连接并延长交y轴于点D,设直线AP的解析式为y=x+ ,把点A和点P的坐标代入得
43=k1+b10=3k1+b1 , k1=23b1= 2
∴直线AP的解析式为:y=23x 2,
当x=0时, y=﹣2, ∴D(0, 2),
∴S△APM=12(xA xP) MD=12×(3 1)×(53+2)=113.
(3)解:在△ABC中,A(3,0),B( 1,0),C(0, 1),tan∠CAB=13,
∴AB=4,AC=32+12=10,
如图3,过点M作MQ垂直于原抛物线的对称轴于点Q,
∴MQ=1,PQ=53+43=3,
∴tan∠MPQ=MQPQ=13,PM=10.
∴∠MPQ=∠CAB,
若△PMN与△ABC相似,则PM:PN=AB:AC或PM:PN=AC:AB,
设N(1,t),
则PN=t+43,
∴10:(t+43)=4:10或10:(t+43)=10:4,
解得t=76或t=83.
∴N(1,76)或(1,83).
一、单选题
1.下列各命题中假命题的是( )
A.全等三角形的对应角相等 B.如果两个数相等,那么它们的绝对值相等
C.两直线平行,同位角相等 D.如果两个角相等,那么这两个角是对顶角
2.中国疫苗撑起全球抗疫“生命线”中国外交部数据显示,截止2021年3月底,我国已无偿向80个国家和3个国际组织提供疫苗援助.预计2022年中国新冠疫苗产能有望达到50亿剂,约占全球的一半,必将为全球抗疫作出重大贡献.数据“50亿”用科学记数法表示为( )
A. B. C. D.
3.下列说法中,正确的是( )
A.“射击运动员射击一次,命中靶心”是必然事件 B.不可能事件发生的概率为0
C.随机事件发生的概率为 D.投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次
4.a,b是有理数,它们在数轴上的对应点的位置如图所示,对于以下结论,正确的是( )
A. B. C. D.
5.如图,已知二次函数 的图像如图所示,有下列5个结论:① ,② ,③ ,④⑤ 。其中正确的结论有( )
A.①②③ B.①③ ④ C.③④⑤ D.②③⑤
6.如图:为了测量某棵树的高度,小刚用长为2m的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点,此时,竹竿与这一点距离6m,与树相距15m,那么这棵的高度为( )
A.5米 B.7米 C.7.5米 D.21米
7.已知,△ABC,△DEF,△XYZ的相关数据如图所示,则( )
A.B. C.D.
8.关于 的一元一次不等式组 的解集为 ,且关于 的分式方程 有整数解,则符合条件的所有整数 的和为( )
A.9 B.10 C.13 D.14
9.设想有一根铁丝套在地球的赤道上,刚好拉紧后,又放长了10米,并使得铁丝均匀地离开地面.则下面说法中比较合理的是( )
A.你只能塞过一张纸 B.只能伸进你的拳头
C.能钻过一只小羊 D.能驶过一艘万吨巨轮
10.如图,点O为正六边形的中心,P,Q分别从点A(1,0)同时出发,沿正六边形按图示方向运动,点P的速度为每秒1个单位长度,点Q的速度为每秒2个单位长度,则第2020次相遇地点的坐标为( )
A. B.
C. D.
二、填空题
11.因式分解:x2﹣2x+1= .
12.直线上依次有A,B,C,D四个点,AD=7,AB=2,若AB,BC,CD可构成以BC为腰的等腰三角形,则BC的长为 .
13.在平面直角坐标系中,点A(x﹣1,2﹣x)关于y轴对称的对称点在第一象限,则实数x的取值范围是 .
14.如图,Rt△AOB中,∠OAB=90°,∠OBA=30°,顶点A在反比例函数y=图象上,若Rt△AOB的面积恰好被y轴平分,则进过点B的反比例函数的解析式为 .
15.已知:如图,四边形ABCD是边长为1的正方形,对角线AC、BD相交于点O.过点O作一直角∠MON,直角边OM、ON分别与OA、OB重合,然后逆时针旋转∠MON,旋转角为θ(0°<θ<90°),OM、ON分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是 (填序号).
① ;②S四边形OEBF:S正方形ABCD=1:2;③ ;④OG BD=AE2+CF2;⑤在旋转过程中,当△BEF与△COF的面积之和最大时, .
三、计算题
16.计算:2sin45°-|1-|+(tan60°-1)0+()-1
17.先化简,再求值:( +2-x)÷ ,其中x满足x2-4x+3=0.
四、作图题
18.如图,两个班的学生分别在C、D两处参加植树劳动,现要在道路AO、OB的交叉区域内(∠AOB的内部)设一个茶水供应点M,M到两条道路的距离相等,且MC=MD,这个茶水供应点的位置应建在何处?请说明理由。(保留作图痕迹,不写作法)
五、解答题
19.甲、乙两家旅行社为了吸引更多的顾客,分别推出赴某地旅游的团体(多于4人)优惠办法.甲旅行社的优惠办法是:买4张全票,其余人按半价优惠;乙旅行社的优惠办法是:所有人都打七五折优惠.已知这两家旅行社的原价均为每人1000元,那么随着团体人数的变化,哪家旅行社的收费更优惠.
20.如图,从甲楼AB的楼顶A,看乙楼CD的楼顶C,仰角为30°,看乙楼(CD)的楼底D,俯角为60°;已知甲楼的高AB=40m.求乙楼CD的高度,(结果精确到1m)
六、综合题
21.随着科技的进步和网络资源的丰富,在线学习已经成为更多人自主学习的选择.某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论.为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图.
请你根据统计图中提供的信息解答下列问题:
(1)求本次调查的学生总人数;
(2)通过计算补全条形统计图;
(3)该校共有学生1800人,请你估计该校对在线阅读最感兴趣的学生有多少人.
22.选择适当的方法解下列方程:
(1) (2)
(3) (4)
(5)
23.如图,矩形中,是边上一动点,过点的反比例函数的图象与边相交于点.
(1)点运动到边的中点时,求反比例函数的表达式; (2)连接,求的值.
24.在平面直角坐标系中,抛物线与x轴交于点A和点B(点A在x轴的正半轴上),与y轴交于点C,已知.
(1)求顶点P和点B的坐标;
(2)将抛物线向右平移2个单位,得到的新抛物线与y轴交于点M,求点M的坐标和的面积;
(3)如果点N在原抛物线的对称轴上,当与相似时,求点N的坐标.
答 案
1.D 2.C 3.B 4.B 5.B 6.A 7.D 8.A 9.C 10.A 11.(x﹣1)2
12.2或2.5 13.x<1 14.10 15.①③④
16.解:2sin45°-|1-|+(tan60°-1)0+()-1=2×+1-+1+2=4.
17.解:原式= ÷ = =- ,
解方程x2-4x+3=0得,
(x-1)(x-3)=0, x1=1,x2=3.
当x=1时,原式无意义;当x=3时,原式=- =- .
18.解:如图,
∠O的平分线和CD的垂直平分线的交点即为茶水供应点的位置.理由是:因为M是∠O的平分线和CD的垂直平分线的交点,所以M到∠O的两边OA和OB的距离相等,M到C、D的距离相等,所以M就是所求.
19.解:设团体有人,收费元
∴,
∵当时,,解得;
∴当时,,解得;
当时,,解得;
∴当团体人数超过8人时,选甲旅行社收费更优惠;
当团体人数为8人时,两家旅行社收费相同;
当团体人数少于8人时,选乙旅行社收费更优惠.
20.解:由题意得:∠AEC=∠AED=90°,AB=DE=40m,∠EAD=60°,∠CAE=30°,
∴, ∴,
∴,
即乙楼CD的高度为53m.
21.(1)解:本次调查的学生总人数为 (人)
∴本次调查的学生总人数为90人;
(2)解:在线听课的人数为: (人)
∴在线听课的人数为36人;
补全的条形统计图如图所示
(3)解: (人)
答:估计该校对在线阅读最感兴趣的学生有480人.
22.(1)解:,移项得:,
提取公因式得:,,,
,;
(2)解:,移项得:,
因式分解得:,
,,,;
(3)解:,
系数化为1得:,
开平方得:,
,,
,;
(4)解:
移项得:,
因式分解得:,
,
;
(5)解:,
移项得:,
去括号得:,
化简得:,
因式分解得:,
,,
,.
23.(1)解:是的中点,
,
点的坐标为,
将点的坐标为代入得:
∴,
∴反比例函数的表达式;
(2)解:点的横坐标为4,代入,
, ,
,
点的纵坐标为3,代入,
,即,,,
所以.
24.(1)解:根据题意可画出函数图象,如图1,
令可得,
∴,即.
在中,,
∴, ∴, ∴.
将点A的坐标代入抛物线解析式可得,,
解得.
∴抛物线的解析式为:.
∴顶点,
令,即,
∴或,
∴.
(2)解:如图2,
将(1)中抛物线向右平移2个单位,得到的新抛物线.
令,则.
∴
连接并延长交y轴于点D,设直线AP的解析式为y=x+ ,把点A和点P的坐标代入得
43=k1+b10=3k1+b1 , k1=23b1= 2
∴直线AP的解析式为:y=23x 2,
当x=0时, y=﹣2, ∴D(0, 2),
∴S△APM=12(xA xP) MD=12×(3 1)×(53+2)=113.
(3)解:在△ABC中,A(3,0),B( 1,0),C(0, 1),tan∠CAB=13,
∴AB=4,AC=32+12=10,
如图3,过点M作MQ垂直于原抛物线的对称轴于点Q,
∴MQ=1,PQ=53+43=3,
∴tan∠MPQ=MQPQ=13,PM=10.
∴∠MPQ=∠CAB,
若△PMN与△ABC相似,则PM:PN=AB:AC或PM:PN=AC:AB,
设N(1,t),
则PN=t+43,
∴10:(t+43)=4:10或10:(t+43)=10:4,
解得t=76或t=83.
∴N(1,76)或(1,83).
同课章节目录
