第七章:平面直角坐标系练习题(含解析)2021-2022学年新疆地区七年级下学期人教版数学期末试题选编
文档属性
| 名称 | 第七章:平面直角坐标系练习题(含解析)2021-2022学年新疆地区七年级下学期人教版数学期末试题选编 |  | |
| 格式 | zip | ||
| 文件大小 | 623.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-29 21:18:16 | ||
图片预览




文档简介
第七章:平面直角坐标系
一、单选题
1.(2022春·新疆喀什·七年级统考期末)在平面直角坐标系中,点P(1,-2)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.(2022春·新疆巴音郭楞·七年级统考期末)在平面直角坐标系中,下列点在y轴上的是( )
A. B. C. D.
3.(2022春·新疆乌鲁木齐·七年级统考期末)已知点在第三象限,则点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.(2022春·新疆乌鲁木齐·七年级统考期末)在平面直角坐标系中,若过不同的两点P(2a,6)与Q(4+b,3-b)的直线PQ∥x轴,则( )
A.a=,b=-3 B.a≠,b≠-3
C.a=,b≠-3 D.a≠,b=-3
5.(2022春·新疆吐鲁番·七年级统考期末)如图,在平面直角坐标系上有个点,点A第1次向上跳动1个单位至点,紧接着第2次向右跳动2个单位至点,第3次向上跳动1个单位,第4次向左跳动3个单位,第5次又向上跳动1个单位,第6次向右跳动4个单位,…,依次规律跳动下去,点第2022次跳动至点的坐标是( )
A. B.
C. D.
6.(2022春·新疆吐鲁番·七年级统考期末)如图是小数在4×4的小正方形组成的网格中画的一张脸的示意图,如果用(0,4)和(2,4)表示眼睛,那么嘴的位置可以表示成( )
A.(2,1) B.(1,1) C.(1,﹣2) D.(1,2)
7.(2022春·新疆克拉玛依·七年级校考期末)若将点A(1,3)向左平移2个单位,再向下平移4个单位得到点B,则点B的坐标为( )
A.(﹣1,0) B.(﹣1,﹣1) C.(﹣2,0) D.(﹣2,﹣1)
8.(2022春·新疆阿克苏·七年级统考期末)若将点A(1,3)向左平移2个单位,再向下平移4个单位得到点B,则点B在第( )象限.
A.一 B.二 C.三 D.四
二、填空题
9.(2022春·新疆乌鲁木齐·七年级统考期末)若点在轴的下方,轴的左方,到轴的距离为,到轴距离为,则点的坐标为______.
10.(2022春·新疆塔城·七年级统考期末)已知点A在第四象限,且到x轴,y轴的距离分别为4、5,则A点的坐标为_________.
11.(2022春·新疆喀什·七年级统考期末)已知点P的坐标是,则点P到y轴的距离是______.
12.(2022春·新疆塔城·七年级统考期末)若,则点在第_________象限.
13.(2022春·新疆克拉玛依·七年级统考期末)在平面直角坐标系中,一个智能机器人接到的指令是:从原点O出发,按“向上→向右→向下→向右→向下→向右→向上→向右”的方向依次不断移动,每次移动1个单位长度,其移动路线如图所示,第一次移动到点A1,第二次移动到点A2,…,第n次移动到点An,则点A2022的坐标是__________.
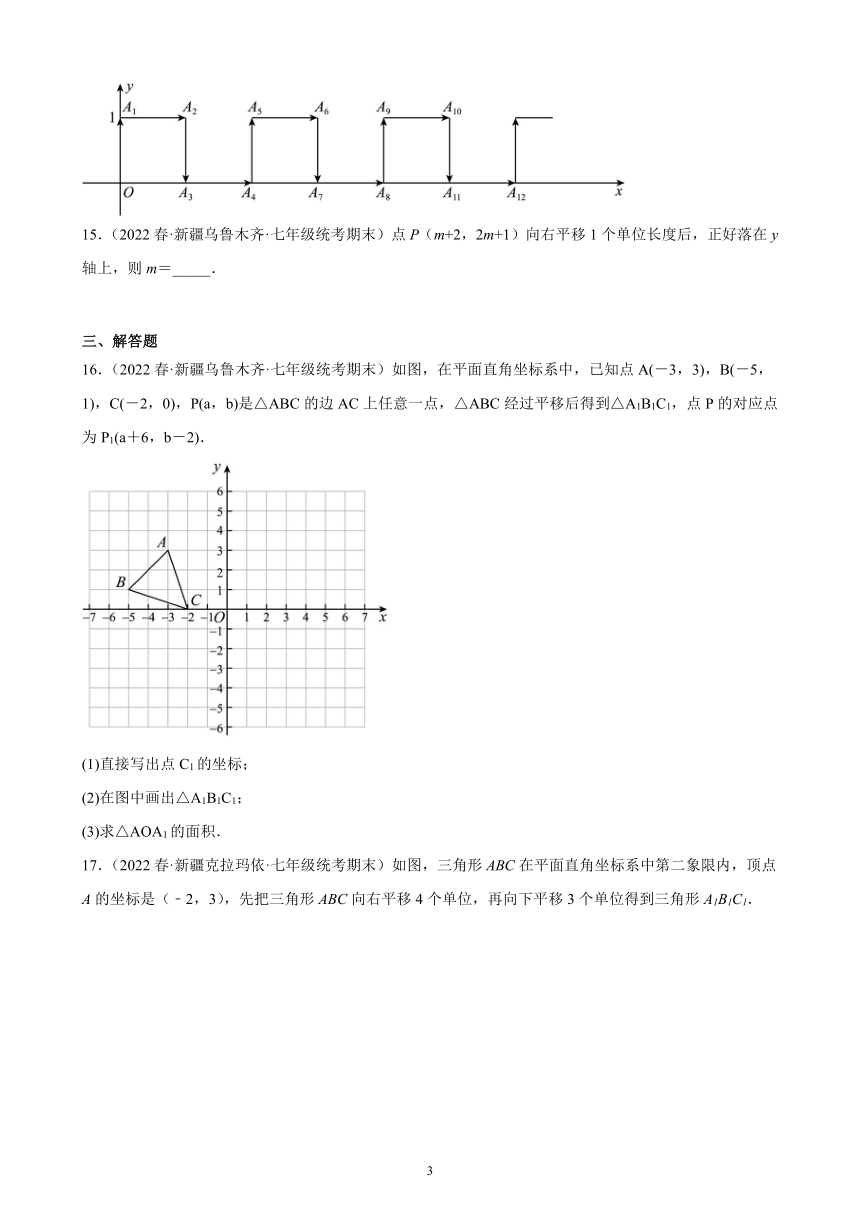
14.(2022春·新疆塔城·七年级统考期末)在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图所示.则点的坐标是_________.
15.(2022春·新疆乌鲁木齐·七年级统考期末)点P(m+2,2m+1)向右平移1个单位长度后,正好落在y轴上,则m=_____.
三、解答题
16.(2022春·新疆乌鲁木齐·七年级统考期末)如图,在平面直角坐标系中,已知点A(-3,3),B(-5,1),C(-2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b-2).
(1)直接写出点C1的坐标;
(2)在图中画出△A1B1C1;
(3)求△AOA1的面积.
17.(2022春·新疆克拉玛依·七年级统考期末)如图,三角形ABC在平面直角坐标系中第二象限内,顶点A的坐标是(﹣2,3),先把三角形ABC向右平移4个单位,再向下平移3个单位得到三角形A1B1C1.
(1)请在图中作出三角形A1B1C1;
(2)点A1的坐标为 ,点B1的坐标为 ,点C1的坐标为 ;
(3)求三角形A1B1C1的面积.
18.(2022春·新疆巴音郭楞·七年级统考期末)如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,三角形ABC的三个顶点均在格点上.
(1)将三角形ABC向左平移5个单位,再向下平移3个单位得到三角形,画出平移后的图形,并写出点的坐标;
(2)求三角形ABC的面积.
19.(2022春·新疆吐鲁番·七年级统考期末)如图,平面直角坐标系中,的顶点都在网格点上.
(1)把向左平移2个单位,再向下平移2个单位,画出平移后的;
(2)写出点、、的坐标.
20.(2022春·新疆喀什·七年级统考期末)如图,在平面直角坐标系中,,,将线段AB先向左平移2个单位,再向上平移3个单位,A、B的对应点分别为D、C.
(1)画出线段CD,并写出C、D两点的坐标;
(2)连接AD、BC,求四边形ABCD的面积.
参考答案:
1.D
【分析】根据各象限内点的坐标特征解答即可.
【详解】∵点P(1,-2),横坐标大于0,纵坐标小于0,
∴点P(1,-2)在第三象限.
故选D
【点睛】本题考查了象限内点的坐标特征,关键是熟记平面直角坐标系中各个象限内点的坐标符号.
2.D
【分析】根据轴上点坐标的特征:横坐标为0,进行判断即可.
【详解】解:A选项,是第二象限点坐标,不符合题意,此选项错误;
B选项,是轴上点坐标,不符合题意,此选项错误;
C选项,是第一象限点坐标,不符合题意,此选项错误;
D选项,是轴上点坐标,符合题意,此选项正确.
故选D.
【点睛】本题考查了平面直角坐标系中轴上点坐标,熟练掌握轴上点坐标的特征是解答本题的关键.
3.A
【分析】根据点在第三象限的条件横坐标是负数,纵坐标是负数,可判断出点坐标中、的符号特点,进而可求出所求的点的横纵坐标的符号,进而判断点所在的象限.
【详解】解:点在第三象限,
,,
,,
点在第一象限.
故选A.
【点睛】本题考查了点的坐标,解决本题的关键是记住平面直角坐标系中各个象限内点的符号,四个象限的符号特点分别是:第一象限;第二象限;第三象限;第四象限.
4.D
【分析】根据平行于x轴的直线上点的纵坐标相等列出方程计算即可得解.
【详解】过不同的两点P(2a,6)与Q(4+b,3-b)的直线PQ∥x轴,
∴2a≠4+b,6=3-b,
解得b=-3,a≠.
故选D.
【点睛】本题考查了坐标与图形,熟记平行于x轴的直线上点的纵坐标相等是解题的关键.
5.B
【分析】设第n次跳动至点A,根据部分点坐标的变化找出变化规律“A4n(﹣n﹣1,2n),A4n+1(﹣n﹣1,2n+1),A4n+2(n+1,2n+1),A4n+3(n+1,2n+2)(n为自然数)”,依此规律结合2022=505×4+2即可得出点A2022的坐标.
【详解】解:设第n次跳动至点A,
观察,发现:A(﹣1,0),A1(﹣1,1),A2(1,1),A3(1,2),A4(﹣2,2),A5(﹣2,3),A6(2,3),A7(2,4),A8(﹣3,4),A9(﹣3,5),…,
∴A4n(﹣n﹣1,2n),A4n+1(﹣n﹣1,2n+1),A4n+2(n+1,2n+1),A4n+3(n+1,2n+2)(n为自然数).
∵2022=505×4+2,
∴A2022(505+1,505×2+1),即(506,1011).
故选:B.
【点睛】本题考查了规律型中点的坐标,根据部分点A坐标的变化找出变化规律“A4n(﹣n﹣1,2n),A4n+1(﹣n﹣1,2n+1),A4n+2(n+1,2n+1),A4n+3(n+1,2n+2)(n为自然数)”是解题的关键.
6.D
【分析】根据左右的眼睛的坐标画出直角坐标系,然后写出嘴的位置对应的点的坐标.
【详解】解:建立平面直角坐标系如图,
嘴的坐标为(1,2).
故选:D.
【点睛】本题考查了坐标确定位置:平面直角坐标系中点与有序实数对一一对应;记住平面内特殊位置的点的坐标特征.
7.B
【详解】解:已知点A(1,3)向左平移2个单位,再向下平移4个单位得到点B,
根据向左平移横坐标减,向下平移纵坐标减的平移规律可得,
点B的横坐标为1﹣2=﹣1,纵坐标为3﹣4=﹣1,
所以B的坐标为(﹣1,﹣1).
故选B.
【点睛】考点:坐标与图形变化﹣平移.
8.C
【分析】根据平移要求求出B的坐标,再判断位置即可得出答案.
【详解】解∶A(1,3)向左平移2个单位,再向下平移4个单位得到点B坐标是(-1,-1),在第三象限.
故选C
【点睛】本题考考查了平移.理解点的平移中坐标变化规律.是解题的关键.
9.
【分析】根据点的位置确定点坐标即可.
【详解】点在轴的下方,
纵坐标为负,
在轴的左方,
横坐标为负,
到轴的距离为,
纵坐标为,
到轴距离为,
横坐标为,
点的坐标为.
故答案为:.
【点睛】此题主要考查了点的坐标.记住各象限内点的坐标的符号是解题的关键,四个象限的符号特点分别是:第一象限;第二象限;第三象限;第四象限.
10.(5,-4)
【分析】已知点A在第四象限内,那么横坐标大于0,纵坐标小于0,进而根据到坐标轴的距离判断具体坐标.
【详解】解:因为点A在第四象限,所以其横、纵坐标分别为正数、负数,
又因为点A到x轴的距离为4,到y轴的距离为5,
所以点A的坐标为(5,-4).
故答案为:(5,-4).
【点睛】本题考查了点的坐标,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
11.3
【分析】点到y的距离是|x|,进而得出答案.
【详解】解:∵P的坐标是,
∴点P到y轴的距离是3.
故答案为:3.
【点睛】本题考查平面直角坐标系中点到坐标轴的距离,准确地理解其知识点是解决问题的关键.
12.四
【分析】由两个非负数相加得0,那么这两个数均为0,得到,的值后,进而根据符号判断点所在象限.
【详解】解:,
,
解得,,
点在第四象限.
故答案为:四.
【点睛】本题主要考查了平面直角坐标系中第二象限的点的坐标的符号特点及非负数的性质.涉及的知识点为:四个象限的符号特点分别是:第一象限;第二象限;第三象限;第四象限.注意两个非负数相加得0,这两个非负数均为0.
13.(1011,-1).
【分析】由点的移动规律发现每移动8次构成一个循环,一个循环相当于向右平移4个单位,用2022÷8即可解决问题.
【详解】解:由题意知:A1 (0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,-1),A6(3,-1),A7(3,0),A8(4,0),
可以发现每移动8次构成一个循环,一个循环相当于向右平移4个单位,
∴2022÷8=252 6,
∴252×4=1008,
∴A2022 (1011,-1),
故答案为:(1011,-1).
【点睛】本题考查了平面直角坐标系中的点的规律探索问题,仔细观察图形,得出每移动8次构成一个循环,一个循环相当于向右平移4个单位结论是解题的关键.
14.(1011,1)
【分析】观察图形,找到点的坐标变化规律,每移动4个点为一个循环,利用规律求解即可.
【详解】解:观察发现:每移动4个点为一个循环,
2022÷4=505……2,
由图可知(1,1),(3,1),(5,1),......,
根据规律可知A的下标为2、6、10、......,
即第n个数可以用4n+1表示,
点的横坐标依次为1、3、5、......,
∴点列......的第n个点为,
当4n+2=2022时,n=505,
∴,
故答案为(1011,1).
【点睛】本题考查了规律型问题在点的坐标问题中的应用,数形结合并正确得出规律是解题的关键.
15.-3
【详解】点P(m+2,2m+1)向右平移1个单位长度后 ,正好落在y轴上,则
故答案为:-3
16.(1)(4,-2);(2)作图见解析,(3)6.
【分析】(1)根据点P的对应点为P1()确定出平移规律为向右6个单位,向下2个单位,,由此规律和C(-2,0)即可求出C1的坐标;(2)根据(1)中的平移规律确定点A、B、C平移后的对应点A1、B1、C1的位置,然后顺次连接即可;(3)利用△AOA1所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可得解.
【详解】(1)∵点P(a,b)的对应点为P1(a+6,b-2),
∴平移规律为向右6个单位,向下2个单位,
∴C(-2,0)的对应点C1的坐标为(4,-2);
(2)△A1B1C1如图所示;
(3)△AOA1的面积=6×3-×3×3-×3×1-×6×2=18---6=18-12=6.
考点:图形的平移变换.
17.(1)见解析;
(2),,;
(3).
【分析】(1)将点A,点B,点C按照向右平移4个单位,再向下平移3个单位的平移方式平移得到点A1,点B1,点C1,再连接各点即可;
(2)利用点A的坐标为,可求出点B,C的坐标,结合坐标点平移的特点求解即可;
(3)利用填补法求面积即可.
【详解】(1)解:三角形A1B1C1如图:
(2)解:∵,
∴,,
∵向右平移4个单位,向下平移3个单位,
∴,,,
故答案为:,,;
(3)解:如图:
利用填补法求面积:.
【点睛】本题考查平移作图,坐标点的平移特点,填补法求面积,解题的关键是掌握平移的特点:左减右加,上加下减.
18.(1)平移后的图形见解析;
(2)6
【分析】(1)利用平移变换的性质分别作出、、的对应点、、,将点、、顺次连接即可画出平移后的图形,根据图形写出点的坐标即可;
(2)以为底,根据图形,找到边对应的高,再根据三角形的面积公式求解即可.
【详解】(1)解:平移后的图形如图所示:
点的坐标为:
(2)解:∵以为底,底的长度为3个单位,高为4个单位
∴
【点睛】本题考查了作图:平移变换,三角形的面积等知识点,掌握平移变换是解答本题的关键.
19.(1)见解析
(2)点、、
【分析】(1)直接利用平移规律得出对应点位置进而得出答案;
(2)利用对应点位置得出点的坐标即可.
(1)
解:如图所示:即为所求;
(2)
解∶根据题意得∶A(2,-1),B(4,3),C(1,2),
∵把向左平移2个单位,再向下平移2个单位得到,
∴点、、.
【点睛】本题主要考查了考查了平移变换,正确得出对应点位置是解题关键.
20.(1)图见解析,,
(2)9
【分析】(1)根据平移方式确定C点和D点的位置即可求解;
(2)利用平行四边形面积公式或用长方形面积减去2个三角形面积求解.
(1)
解:将,分别向左平移2个单位,再向上平移3个单位,得到D、C,连接C、D即可得到线段CD,
如下图所示,,;
(2)
解:如下图所示,连接AD、BC.
四边形ABCD的面积或.
【点睛】本题考查平面直角坐标系和图形的平移,能够根据平移方式确定平移后对应点的位置是解题的关键.
一、单选题
1.(2022春·新疆喀什·七年级统考期末)在平面直角坐标系中,点P(1,-2)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.(2022春·新疆巴音郭楞·七年级统考期末)在平面直角坐标系中,下列点在y轴上的是( )
A. B. C. D.
3.(2022春·新疆乌鲁木齐·七年级统考期末)已知点在第三象限,则点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.(2022春·新疆乌鲁木齐·七年级统考期末)在平面直角坐标系中,若过不同的两点P(2a,6)与Q(4+b,3-b)的直线PQ∥x轴,则( )
A.a=,b=-3 B.a≠,b≠-3
C.a=,b≠-3 D.a≠,b=-3
5.(2022春·新疆吐鲁番·七年级统考期末)如图,在平面直角坐标系上有个点,点A第1次向上跳动1个单位至点,紧接着第2次向右跳动2个单位至点,第3次向上跳动1个单位,第4次向左跳动3个单位,第5次又向上跳动1个单位,第6次向右跳动4个单位,…,依次规律跳动下去,点第2022次跳动至点的坐标是( )
A. B.
C. D.
6.(2022春·新疆吐鲁番·七年级统考期末)如图是小数在4×4的小正方形组成的网格中画的一张脸的示意图,如果用(0,4)和(2,4)表示眼睛,那么嘴的位置可以表示成( )
A.(2,1) B.(1,1) C.(1,﹣2) D.(1,2)
7.(2022春·新疆克拉玛依·七年级校考期末)若将点A(1,3)向左平移2个单位,再向下平移4个单位得到点B,则点B的坐标为( )
A.(﹣1,0) B.(﹣1,﹣1) C.(﹣2,0) D.(﹣2,﹣1)
8.(2022春·新疆阿克苏·七年级统考期末)若将点A(1,3)向左平移2个单位,再向下平移4个单位得到点B,则点B在第( )象限.
A.一 B.二 C.三 D.四
二、填空题
9.(2022春·新疆乌鲁木齐·七年级统考期末)若点在轴的下方,轴的左方,到轴的距离为,到轴距离为,则点的坐标为______.
10.(2022春·新疆塔城·七年级统考期末)已知点A在第四象限,且到x轴,y轴的距离分别为4、5,则A点的坐标为_________.
11.(2022春·新疆喀什·七年级统考期末)已知点P的坐标是,则点P到y轴的距离是______.
12.(2022春·新疆塔城·七年级统考期末)若,则点在第_________象限.
13.(2022春·新疆克拉玛依·七年级统考期末)在平面直角坐标系中,一个智能机器人接到的指令是:从原点O出发,按“向上→向右→向下→向右→向下→向右→向上→向右”的方向依次不断移动,每次移动1个单位长度,其移动路线如图所示,第一次移动到点A1,第二次移动到点A2,…,第n次移动到点An,则点A2022的坐标是__________.
14.(2022春·新疆塔城·七年级统考期末)在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图所示.则点的坐标是_________.
15.(2022春·新疆乌鲁木齐·七年级统考期末)点P(m+2,2m+1)向右平移1个单位长度后,正好落在y轴上,则m=_____.
三、解答题
16.(2022春·新疆乌鲁木齐·七年级统考期末)如图,在平面直角坐标系中,已知点A(-3,3),B(-5,1),C(-2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b-2).
(1)直接写出点C1的坐标;
(2)在图中画出△A1B1C1;
(3)求△AOA1的面积.
17.(2022春·新疆克拉玛依·七年级统考期末)如图,三角形ABC在平面直角坐标系中第二象限内,顶点A的坐标是(﹣2,3),先把三角形ABC向右平移4个单位,再向下平移3个单位得到三角形A1B1C1.
(1)请在图中作出三角形A1B1C1;
(2)点A1的坐标为 ,点B1的坐标为 ,点C1的坐标为 ;
(3)求三角形A1B1C1的面积.
18.(2022春·新疆巴音郭楞·七年级统考期末)如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,三角形ABC的三个顶点均在格点上.
(1)将三角形ABC向左平移5个单位,再向下平移3个单位得到三角形,画出平移后的图形,并写出点的坐标;
(2)求三角形ABC的面积.
19.(2022春·新疆吐鲁番·七年级统考期末)如图,平面直角坐标系中,的顶点都在网格点上.
(1)把向左平移2个单位,再向下平移2个单位,画出平移后的;
(2)写出点、、的坐标.
20.(2022春·新疆喀什·七年级统考期末)如图,在平面直角坐标系中,,,将线段AB先向左平移2个单位,再向上平移3个单位,A、B的对应点分别为D、C.
(1)画出线段CD,并写出C、D两点的坐标;
(2)连接AD、BC,求四边形ABCD的面积.
参考答案:
1.D
【分析】根据各象限内点的坐标特征解答即可.
【详解】∵点P(1,-2),横坐标大于0,纵坐标小于0,
∴点P(1,-2)在第三象限.
故选D
【点睛】本题考查了象限内点的坐标特征,关键是熟记平面直角坐标系中各个象限内点的坐标符号.
2.D
【分析】根据轴上点坐标的特征:横坐标为0,进行判断即可.
【详解】解:A选项,是第二象限点坐标,不符合题意,此选项错误;
B选项,是轴上点坐标,不符合题意,此选项错误;
C选项,是第一象限点坐标,不符合题意,此选项错误;
D选项,是轴上点坐标,符合题意,此选项正确.
故选D.
【点睛】本题考查了平面直角坐标系中轴上点坐标,熟练掌握轴上点坐标的特征是解答本题的关键.
3.A
【分析】根据点在第三象限的条件横坐标是负数,纵坐标是负数,可判断出点坐标中、的符号特点,进而可求出所求的点的横纵坐标的符号,进而判断点所在的象限.
【详解】解:点在第三象限,
,,
,,
点在第一象限.
故选A.
【点睛】本题考查了点的坐标,解决本题的关键是记住平面直角坐标系中各个象限内点的符号,四个象限的符号特点分别是:第一象限;第二象限;第三象限;第四象限.
4.D
【分析】根据平行于x轴的直线上点的纵坐标相等列出方程计算即可得解.
【详解】过不同的两点P(2a,6)与Q(4+b,3-b)的直线PQ∥x轴,
∴2a≠4+b,6=3-b,
解得b=-3,a≠.
故选D.
【点睛】本题考查了坐标与图形,熟记平行于x轴的直线上点的纵坐标相等是解题的关键.
5.B
【分析】设第n次跳动至点A,根据部分点坐标的变化找出变化规律“A4n(﹣n﹣1,2n),A4n+1(﹣n﹣1,2n+1),A4n+2(n+1,2n+1),A4n+3(n+1,2n+2)(n为自然数)”,依此规律结合2022=505×4+2即可得出点A2022的坐标.
【详解】解:设第n次跳动至点A,
观察,发现:A(﹣1,0),A1(﹣1,1),A2(1,1),A3(1,2),A4(﹣2,2),A5(﹣2,3),A6(2,3),A7(2,4),A8(﹣3,4),A9(﹣3,5),…,
∴A4n(﹣n﹣1,2n),A4n+1(﹣n﹣1,2n+1),A4n+2(n+1,2n+1),A4n+3(n+1,2n+2)(n为自然数).
∵2022=505×4+2,
∴A2022(505+1,505×2+1),即(506,1011).
故选:B.
【点睛】本题考查了规律型中点的坐标,根据部分点A坐标的变化找出变化规律“A4n(﹣n﹣1,2n),A4n+1(﹣n﹣1,2n+1),A4n+2(n+1,2n+1),A4n+3(n+1,2n+2)(n为自然数)”是解题的关键.
6.D
【分析】根据左右的眼睛的坐标画出直角坐标系,然后写出嘴的位置对应的点的坐标.
【详解】解:建立平面直角坐标系如图,
嘴的坐标为(1,2).
故选:D.
【点睛】本题考查了坐标确定位置:平面直角坐标系中点与有序实数对一一对应;记住平面内特殊位置的点的坐标特征.
7.B
【详解】解:已知点A(1,3)向左平移2个单位,再向下平移4个单位得到点B,
根据向左平移横坐标减,向下平移纵坐标减的平移规律可得,
点B的横坐标为1﹣2=﹣1,纵坐标为3﹣4=﹣1,
所以B的坐标为(﹣1,﹣1).
故选B.
【点睛】考点:坐标与图形变化﹣平移.
8.C
【分析】根据平移要求求出B的坐标,再判断位置即可得出答案.
【详解】解∶A(1,3)向左平移2个单位,再向下平移4个单位得到点B坐标是(-1,-1),在第三象限.
故选C
【点睛】本题考考查了平移.理解点的平移中坐标变化规律.是解题的关键.
9.
【分析】根据点的位置确定点坐标即可.
【详解】点在轴的下方,
纵坐标为负,
在轴的左方,
横坐标为负,
到轴的距离为,
纵坐标为,
到轴距离为,
横坐标为,
点的坐标为.
故答案为:.
【点睛】此题主要考查了点的坐标.记住各象限内点的坐标的符号是解题的关键,四个象限的符号特点分别是:第一象限;第二象限;第三象限;第四象限.
10.(5,-4)
【分析】已知点A在第四象限内,那么横坐标大于0,纵坐标小于0,进而根据到坐标轴的距离判断具体坐标.
【详解】解:因为点A在第四象限,所以其横、纵坐标分别为正数、负数,
又因为点A到x轴的距离为4,到y轴的距离为5,
所以点A的坐标为(5,-4).
故答案为:(5,-4).
【点睛】本题考查了点的坐标,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
11.3
【分析】点到y的距离是|x|,进而得出答案.
【详解】解:∵P的坐标是,
∴点P到y轴的距离是3.
故答案为:3.
【点睛】本题考查平面直角坐标系中点到坐标轴的距离,准确地理解其知识点是解决问题的关键.
12.四
【分析】由两个非负数相加得0,那么这两个数均为0,得到,的值后,进而根据符号判断点所在象限.
【详解】解:,
,
解得,,
点在第四象限.
故答案为:四.
【点睛】本题主要考查了平面直角坐标系中第二象限的点的坐标的符号特点及非负数的性质.涉及的知识点为:四个象限的符号特点分别是:第一象限;第二象限;第三象限;第四象限.注意两个非负数相加得0,这两个非负数均为0.
13.(1011,-1).
【分析】由点的移动规律发现每移动8次构成一个循环,一个循环相当于向右平移4个单位,用2022÷8即可解决问题.
【详解】解:由题意知:A1 (0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,-1),A6(3,-1),A7(3,0),A8(4,0),
可以发现每移动8次构成一个循环,一个循环相当于向右平移4个单位,
∴2022÷8=252 6,
∴252×4=1008,
∴A2022 (1011,-1),
故答案为:(1011,-1).
【点睛】本题考查了平面直角坐标系中的点的规律探索问题,仔细观察图形,得出每移动8次构成一个循环,一个循环相当于向右平移4个单位结论是解题的关键.
14.(1011,1)
【分析】观察图形,找到点的坐标变化规律,每移动4个点为一个循环,利用规律求解即可.
【详解】解:观察发现:每移动4个点为一个循环,
2022÷4=505……2,
由图可知(1,1),(3,1),(5,1),......,
根据规律可知A的下标为2、6、10、......,
即第n个数可以用4n+1表示,
点的横坐标依次为1、3、5、......,
∴点列......的第n个点为,
当4n+2=2022时,n=505,
∴,
故答案为(1011,1).
【点睛】本题考查了规律型问题在点的坐标问题中的应用,数形结合并正确得出规律是解题的关键.
15.-3
【详解】点P(m+2,2m+1)向右平移1个单位长度后 ,正好落在y轴上,则
故答案为:-3
16.(1)(4,-2);(2)作图见解析,(3)6.
【分析】(1)根据点P的对应点为P1()确定出平移规律为向右6个单位,向下2个单位,,由此规律和C(-2,0)即可求出C1的坐标;(2)根据(1)中的平移规律确定点A、B、C平移后的对应点A1、B1、C1的位置,然后顺次连接即可;(3)利用△AOA1所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可得解.
【详解】(1)∵点P(a,b)的对应点为P1(a+6,b-2),
∴平移规律为向右6个单位,向下2个单位,
∴C(-2,0)的对应点C1的坐标为(4,-2);
(2)△A1B1C1如图所示;
(3)△AOA1的面积=6×3-×3×3-×3×1-×6×2=18---6=18-12=6.
考点:图形的平移变换.
17.(1)见解析;
(2),,;
(3).
【分析】(1)将点A,点B,点C按照向右平移4个单位,再向下平移3个单位的平移方式平移得到点A1,点B1,点C1,再连接各点即可;
(2)利用点A的坐标为,可求出点B,C的坐标,结合坐标点平移的特点求解即可;
(3)利用填补法求面积即可.
【详解】(1)解:三角形A1B1C1如图:
(2)解:∵,
∴,,
∵向右平移4个单位,向下平移3个单位,
∴,,,
故答案为:,,;
(3)解:如图:
利用填补法求面积:.
【点睛】本题考查平移作图,坐标点的平移特点,填补法求面积,解题的关键是掌握平移的特点:左减右加,上加下减.
18.(1)平移后的图形见解析;
(2)6
【分析】(1)利用平移变换的性质分别作出、、的对应点、、,将点、、顺次连接即可画出平移后的图形,根据图形写出点的坐标即可;
(2)以为底,根据图形,找到边对应的高,再根据三角形的面积公式求解即可.
【详解】(1)解:平移后的图形如图所示:
点的坐标为:
(2)解:∵以为底,底的长度为3个单位,高为4个单位
∴
【点睛】本题考查了作图:平移变换,三角形的面积等知识点,掌握平移变换是解答本题的关键.
19.(1)见解析
(2)点、、
【分析】(1)直接利用平移规律得出对应点位置进而得出答案;
(2)利用对应点位置得出点的坐标即可.
(1)
解:如图所示:即为所求;
(2)
解∶根据题意得∶A(2,-1),B(4,3),C(1,2),
∵把向左平移2个单位,再向下平移2个单位得到,
∴点、、.
【点睛】本题主要考查了考查了平移变换,正确得出对应点位置是解题关键.
20.(1)图见解析,,
(2)9
【分析】(1)根据平移方式确定C点和D点的位置即可求解;
(2)利用平行四边形面积公式或用长方形面积减去2个三角形面积求解.
(1)
解:将,分别向左平移2个单位,再向上平移3个单位,得到D、C,连接C、D即可得到线段CD,
如下图所示,,;
(2)
解:如下图所示,连接AD、BC.
四边形ABCD的面积或.
【点睛】本题考查平面直角坐标系和图形的平移,能够根据平移方式确定平移后对应点的位置是解题的关键.
