福建省厦门2022-2023学年九年级下学期期中诊断练习数学试题(无答案)
文档属性
| 名称 | 福建省厦门2022-2023学年九年级下学期期中诊断练习数学试题(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 342.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-29 00:00:00 | ||
图片预览


文档简介
福建省厦门2022-2023学年(下)4月阶段性诊断练习
初三年数学试卷
一、选择题(每小题4分,共40分)
1.7的相反数是( )
A.7 B.-7 C. D.
2.下列运算正确的是( )
A.2x-y=-xy B.x-2x=-x C. D.
3.北京时间2022年4月16日09时56分,神舟十三号载人飞船返回舱在东风着陆场成功着陆,神舟十三号载人飞行任务取得圆满成功.神舟十三号载人飞船飞行过程中距离地球最远约为360000米,这个数据用科学记数法表示为( )
A.米 B.米 C.米 D.米
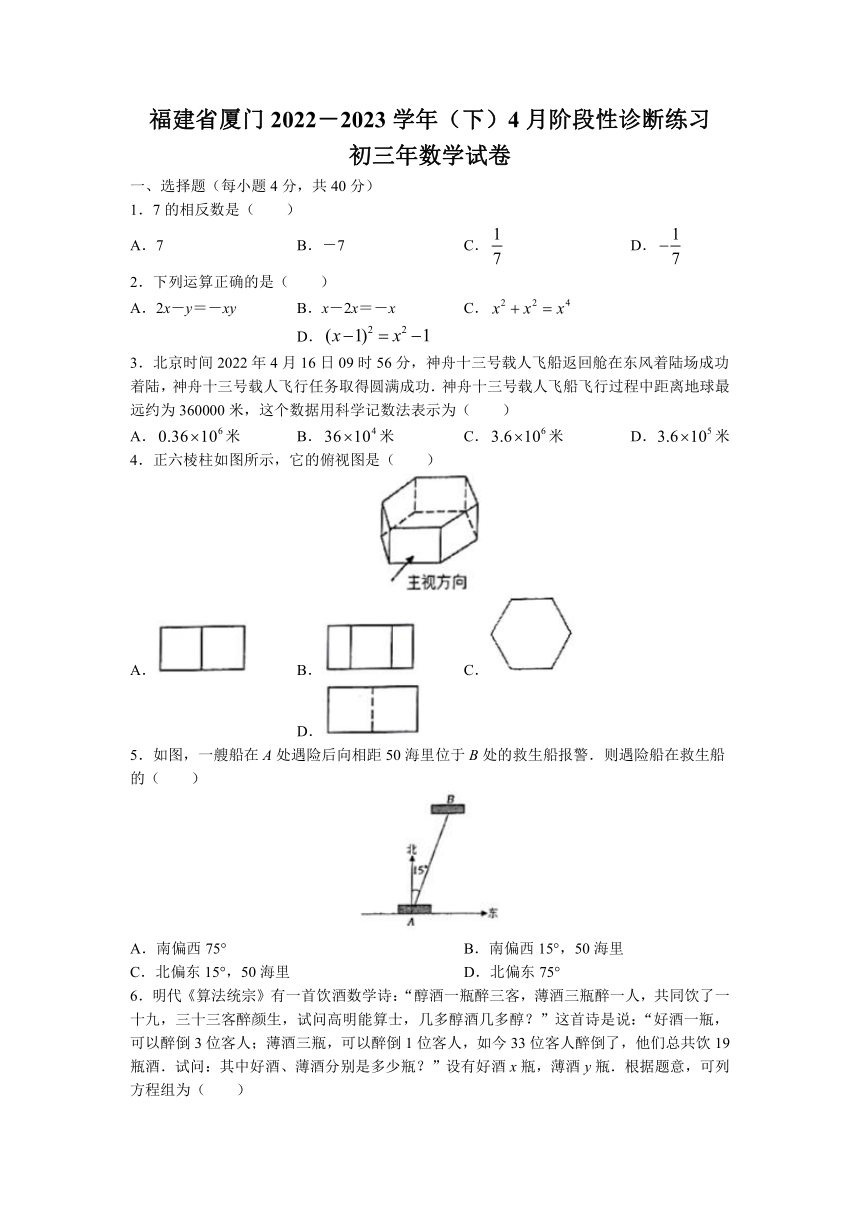
4.正六棱柱如图所示,它的俯视图是( )
A. B. C. D.
5.如图,一艘船在A处遇险后向相距50海里位于B处的救生船报警.则遇险船在救生船的( )
A.南偏西75° B.南偏西15°,50海里
C.北偏东15°,50海里 D.北偏东75°
6.明代《算法统宗》有一首饮酒数学诗:“醇酒一瓶醉三客,薄酒三瓶醉一人,共同饮了一十九,三十三客醉颜生,试问高明能算士,几多醇酒几多醇?”这首诗是说:“好酒一瓶,可以醉倒3位客人;薄酒三瓶,可以醉倒1位客人,如今33位客人醉倒了,他们总共饮19瓶酒.试问:其中好酒、薄酒分别是多少瓶?”设有好酒x瓶,薄酒y瓶.根据题意,可列方程组为( )
A. B. C. D.
7.估计的值应在( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
8.如图,在,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为( )
A.4 B.8 C.6 D.10
9.如图4,在中,∠ACB=90°,点P以每秒1cm的速度从点A出发,沿折线AC-CB运动,到点B停止.过点P作,垂足为D,PD的长y(cm)与点P的运动时间x(秒)的函数图象5如图所示.当点P运动5秒时,PD的长是( )
A.0.8cm B.1.2cm C.1.6cm D.2.4cm
10.已知点、、在二次函数的图象上,且C为抛物线的顶点.若,则m的取值范围是( )
A.m<-3 B.m>-3 C.m<-2 D.m>-2
二、填空题(每小题4分,共24分)
11.若式子在实数范围内有意义,则x的取值范围是______.
12.点到x轴的距离是______.
13.小明解分式方程的过程如下.
解:去分母,得3=2x-(3x+3).①
去括号,得3=2x-3x+3.②
移项、合并同类项,得-x=6.③
化系数为1,得x=-6.④
以上步骤中,开始出错的一步是______(填写对应序号).
14.经过某十字路口的汽车,可能直行,也可能向左转或向右转,如果这三种可能性大小相同,那么两辆汽车经过这个十字路口时,第一辆车向左转,第二辆车向右转的概率是______.
15.如图,四边形ABCD是的内接四边形,两组对边的延长线分别相交于点E、F,且∠E=40°,∠F=60°,则∠A=______.
16.如图,在平面直角坐标系xOy中,菱形ABCD的顶点,,点B,D在反比例函数的图象上,对角线BD交AC于点M,交x轴于点N,若,则k的值是______.
三、解答题(本大题共9题,共86分)
17.(8分)(1)计算:.
(2)解不等式组:,并写出该不等式组的非负整数解.
18.(8分)先化简,再求值:,其中.
19.(8分)如图,在中,AB=AC,D、E是BC边上的点,且BD=CE.求证:AD=AE.
20.(8分)王大伯承包了一个鱼塘,投放了2000条某种鱼苗,经过一段时间的精心喂养,存活率大致达到了90%.他近期想出售鱼塘里的这种鱼.为了估计鱼塘里这种鱼的总质量,王大伯随机捕捞了20条鱼,分别称得其质量后放回鱼塘.
现将这20条鱼的质量作为样本,统计结果如图所示:
(1)这20条鱼质量的中位数是______kg,众数是______kg.
(2)经了解,近期市场上这种鱼的售价为每千克10元,请利用这个样本的平均数,估计王大伯近期售完鱼塘里的这种鱼可收入多少元?
21.(8分)为了解决雨季时城市内涝的难题,我市决定对部分老街道的地下管网进行改造.在改造一段长3600米的街道地下管网时,每天的施工效率比原计划提高了20%,按这样的进度可以比原计划提前10天完成任务.
(1)求实际施工时,每天改造管网的长度;
(2)施工进行20天后,为了减少对交通的影响,施工单位决定再次加快施工进度,以确保总工期不超过40天,那么以后每天改造管网至少还要增加多少米?
22.(10分)如图,已知点M是的外心,在的外部找一点D,使得点D到射线AB和射线AC距离相等,且∠BDC+∠BAC=180°,
(1)请用尺规作图的方法确定点D的位置(不写作法,保留作图痕迹);
(2)若AB=6,AC=4,∠BAC=60°,求线段AD的长.
23.(12分)如图11,灌溉车沿着平行于绿化带底部边线l的方向行驶,为绿化带浇水.喷水口H离地竖直高度为h(单位:m).如图12,可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象;把绿化带横截面抽象为矩形DEFG,其水平宽度DE=3m,竖直高度为EF的长.下边缘抛物线是由上边缘抛物线向左平移得到,上边缘抛物线最高点A离喷水口的水平距离为2m,高出喷水口0.5m,灌溉车到l的距离OD为d(单位:m).
(1)若h=1.5,EF=0.5m.
①求上边缘抛物线的函数解析式.
②求下边缘抛物线与x轴的正半轴交点B的坐标.
③要使灌溉车行驶时喷出的水能浇灌到整个绿化带,求d的取值范围.
(2)若EF=1m,要使灌溉车行驶时喷出的水能浇灌到整个绿化带,请直接写出h的最小值.
24.(12分)我们不妨定义:一组对边平行且一组对角互余的四边形称为“求真四边形”.
(1)如图13,四边形ABCD是“求真四边形”,,若,请用含的代数式表示∠D;
(2)如图14,AB是半圆O的直径,点C、D、E在半圆上(点C、D、E按逆时针排列),AC,BE相交于点F.若∠DCA=∠CBE,求证:四边形DEFC是“求真四边形”;
(3)在(2)的条件下,连接DF,已知,若∠CDF为直角,求的值.
25.(12分)如图,抛物线交x轴于A、B两点(点A在点B的左侧),交y轴负半轴于C点,已知.
(1)求抛物线的解析式;
(2)在直线BC下方的抛物线上取一点P,连接AP交BC于E点,当时,求点P的坐标;
(3)点M、N均在抛物线上,设点M的横坐标为m,点N的横坐标为n,(0<n<m<3),连接MN,连接AM、AN分别与y轴交于点S、T,∠AMN=2∠BAM,请问3OS+ST是否为定值?若是,求出其值;若不是,说明理由.
初三年数学试卷
一、选择题(每小题4分,共40分)
1.7的相反数是( )
A.7 B.-7 C. D.
2.下列运算正确的是( )
A.2x-y=-xy B.x-2x=-x C. D.
3.北京时间2022年4月16日09时56分,神舟十三号载人飞船返回舱在东风着陆场成功着陆,神舟十三号载人飞行任务取得圆满成功.神舟十三号载人飞船飞行过程中距离地球最远约为360000米,这个数据用科学记数法表示为( )
A.米 B.米 C.米 D.米
4.正六棱柱如图所示,它的俯视图是( )
A. B. C. D.
5.如图,一艘船在A处遇险后向相距50海里位于B处的救生船报警.则遇险船在救生船的( )
A.南偏西75° B.南偏西15°,50海里
C.北偏东15°,50海里 D.北偏东75°
6.明代《算法统宗》有一首饮酒数学诗:“醇酒一瓶醉三客,薄酒三瓶醉一人,共同饮了一十九,三十三客醉颜生,试问高明能算士,几多醇酒几多醇?”这首诗是说:“好酒一瓶,可以醉倒3位客人;薄酒三瓶,可以醉倒1位客人,如今33位客人醉倒了,他们总共饮19瓶酒.试问:其中好酒、薄酒分别是多少瓶?”设有好酒x瓶,薄酒y瓶.根据题意,可列方程组为( )
A. B. C. D.
7.估计的值应在( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
8.如图,在,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为( )
A.4 B.8 C.6 D.10
9.如图4,在中,∠ACB=90°,点P以每秒1cm的速度从点A出发,沿折线AC-CB运动,到点B停止.过点P作,垂足为D,PD的长y(cm)与点P的运动时间x(秒)的函数图象5如图所示.当点P运动5秒时,PD的长是( )
A.0.8cm B.1.2cm C.1.6cm D.2.4cm
10.已知点、、在二次函数的图象上,且C为抛物线的顶点.若,则m的取值范围是( )
A.m<-3 B.m>-3 C.m<-2 D.m>-2
二、填空题(每小题4分,共24分)
11.若式子在实数范围内有意义,则x的取值范围是______.
12.点到x轴的距离是______.
13.小明解分式方程的过程如下.
解:去分母,得3=2x-(3x+3).①
去括号,得3=2x-3x+3.②
移项、合并同类项,得-x=6.③
化系数为1,得x=-6.④
以上步骤中,开始出错的一步是______(填写对应序号).
14.经过某十字路口的汽车,可能直行,也可能向左转或向右转,如果这三种可能性大小相同,那么两辆汽车经过这个十字路口时,第一辆车向左转,第二辆车向右转的概率是______.
15.如图,四边形ABCD是的内接四边形,两组对边的延长线分别相交于点E、F,且∠E=40°,∠F=60°,则∠A=______.
16.如图,在平面直角坐标系xOy中,菱形ABCD的顶点,,点B,D在反比例函数的图象上,对角线BD交AC于点M,交x轴于点N,若,则k的值是______.
三、解答题(本大题共9题,共86分)
17.(8分)(1)计算:.
(2)解不等式组:,并写出该不等式组的非负整数解.
18.(8分)先化简,再求值:,其中.
19.(8分)如图,在中,AB=AC,D、E是BC边上的点,且BD=CE.求证:AD=AE.
20.(8分)王大伯承包了一个鱼塘,投放了2000条某种鱼苗,经过一段时间的精心喂养,存活率大致达到了90%.他近期想出售鱼塘里的这种鱼.为了估计鱼塘里这种鱼的总质量,王大伯随机捕捞了20条鱼,分别称得其质量后放回鱼塘.
现将这20条鱼的质量作为样本,统计结果如图所示:
(1)这20条鱼质量的中位数是______kg,众数是______kg.
(2)经了解,近期市场上这种鱼的售价为每千克10元,请利用这个样本的平均数,估计王大伯近期售完鱼塘里的这种鱼可收入多少元?
21.(8分)为了解决雨季时城市内涝的难题,我市决定对部分老街道的地下管网进行改造.在改造一段长3600米的街道地下管网时,每天的施工效率比原计划提高了20%,按这样的进度可以比原计划提前10天完成任务.
(1)求实际施工时,每天改造管网的长度;
(2)施工进行20天后,为了减少对交通的影响,施工单位决定再次加快施工进度,以确保总工期不超过40天,那么以后每天改造管网至少还要增加多少米?
22.(10分)如图,已知点M是的外心,在的外部找一点D,使得点D到射线AB和射线AC距离相等,且∠BDC+∠BAC=180°,
(1)请用尺规作图的方法确定点D的位置(不写作法,保留作图痕迹);
(2)若AB=6,AC=4,∠BAC=60°,求线段AD的长.
23.(12分)如图11,灌溉车沿着平行于绿化带底部边线l的方向行驶,为绿化带浇水.喷水口H离地竖直高度为h(单位:m).如图12,可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象;把绿化带横截面抽象为矩形DEFG,其水平宽度DE=3m,竖直高度为EF的长.下边缘抛物线是由上边缘抛物线向左平移得到,上边缘抛物线最高点A离喷水口的水平距离为2m,高出喷水口0.5m,灌溉车到l的距离OD为d(单位:m).
(1)若h=1.5,EF=0.5m.
①求上边缘抛物线的函数解析式.
②求下边缘抛物线与x轴的正半轴交点B的坐标.
③要使灌溉车行驶时喷出的水能浇灌到整个绿化带,求d的取值范围.
(2)若EF=1m,要使灌溉车行驶时喷出的水能浇灌到整个绿化带,请直接写出h的最小值.
24.(12分)我们不妨定义:一组对边平行且一组对角互余的四边形称为“求真四边形”.
(1)如图13,四边形ABCD是“求真四边形”,,若,请用含的代数式表示∠D;
(2)如图14,AB是半圆O的直径,点C、D、E在半圆上(点C、D、E按逆时针排列),AC,BE相交于点F.若∠DCA=∠CBE,求证:四边形DEFC是“求真四边形”;
(3)在(2)的条件下,连接DF,已知,若∠CDF为直角,求的值.
25.(12分)如图,抛物线交x轴于A、B两点(点A在点B的左侧),交y轴负半轴于C点,已知.
(1)求抛物线的解析式;
(2)在直线BC下方的抛物线上取一点P,连接AP交BC于E点,当时,求点P的坐标;
(3)点M、N均在抛物线上,设点M的横坐标为m,点N的横坐标为n,(0<n<m<3),连接MN,连接AM、AN分别与y轴交于点S、T,∠AMN=2∠BAM,请问3OS+ST是否为定值?若是,求出其值;若不是,说明理由.
同课章节目录
