第十八章:平行四边形练习题(含解析)2021-2022学年新疆地区八年级下学期人教版数学期末试题选编
文档属性
| 名称 | 第十八章:平行四边形练习题(含解析)2021-2022学年新疆地区八年级下学期人教版数学期末试题选编 |  | |
| 格式 | zip | ||
| 文件大小 | 771.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-29 21:05:39 | ||
图片预览


文档简介
第十八章:平行四边形
一、单选题
1.(2022春·新疆克拉玛依·八年级统考期末)如图, ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )
A.10 B.14 C.20 D.22
2.(2022春·新疆塔城·八年级统考期末)如果四边形ABCD是平行四边形,AB=6,且AB的长是四边形ABCD周长的,那么BC的长是( )
A.6 B.8 C.10 D.16
3.(2022春·新疆克拉玛依·八年级统考期末)如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A., B.,
C., D.,
4.(2022春·新疆阿克苏·八年级统考期末)如图,将矩形ABCD沿对角线BD折叠,使点C落在F处,BF交AD于点E.若∠BDC=62°,则∠DEF的度数为( )
A.31° B.28° C.62° D.56°
5.(2022春·新疆塔城·八年级统考期末)如图,在中,,点F为AC中点,是的中位线,若,则BF=( )
A.6 B.4 C.3 D.5
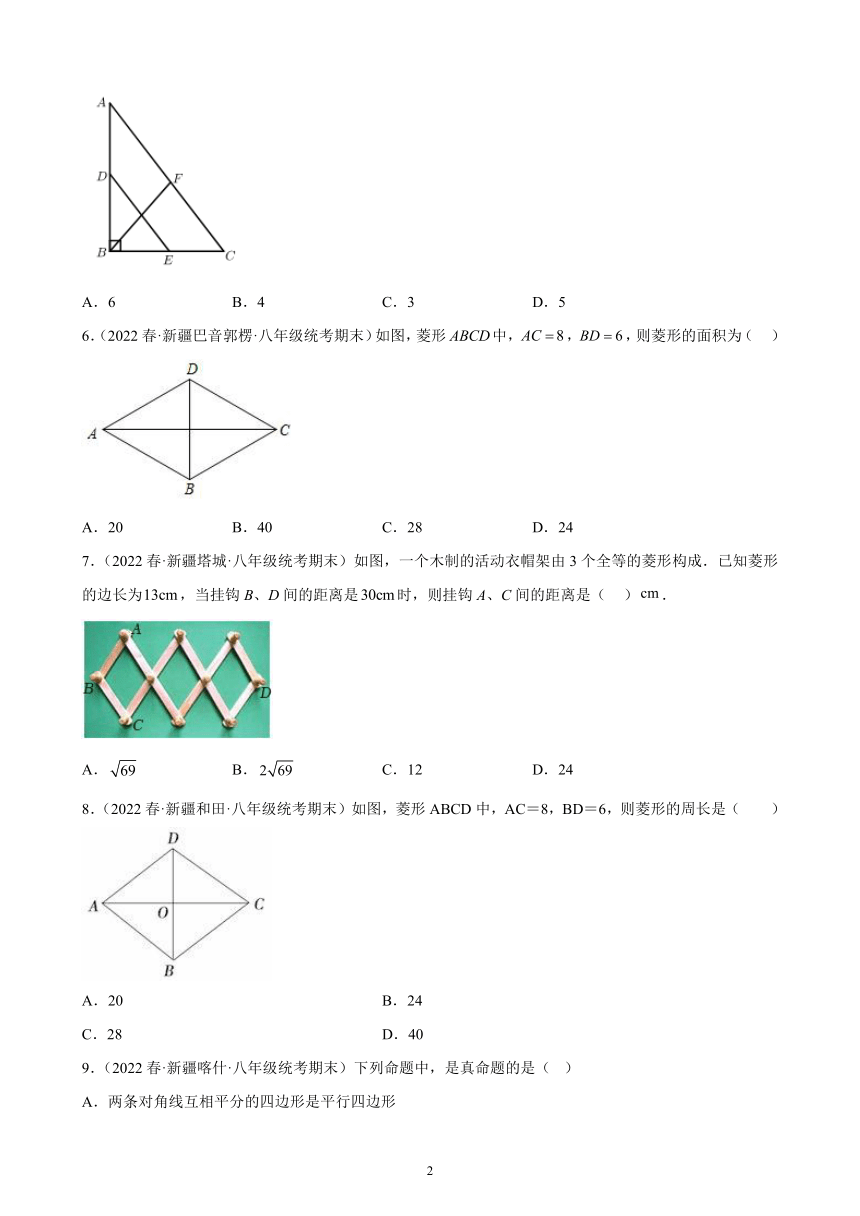
6.(2022春·新疆巴音郭楞·八年级统考期末)如图,菱形中,,,则菱形的面积为( )
A.20 B.40 C.28 D.24
7.(2022春·新疆塔城·八年级统考期末)如图,一个木制的活动衣帽架由3个全等的菱形构成.已知菱形的边长为,当挂钩B、D间的距离是时,则挂钩A、C间的距离是( ).
A. B. C.12 D.24
8.(2022春·新疆和田·八年级统考期末)如图,菱形ABCD中,AC=8,BD=6,则菱形的周长是( )
A.20 B.24
C.28 D.40
9.(2022春·新疆喀什·八年级统考期末)下列命题中,是真命题的是( )
A.两条对角线互相平分的四边形是平行四边形
B.两条对角线相等的四边形是矩形
C.两条对角线互相垂直的四边形是菱形
D.两条对角线互相垂直且相等的四边形是正方形
10.(2022春·新疆克拉玛依·八年级统考期末)如图,点E、F、G、H分别是四边形ABCD边AB、BC、CD、DA的中点.则下列说法:
①若AC=BD,则四边形EFGH为矩形;
②若AC⊥BD,则四边形EFGH为菱形;
③若四边形EFGH是平行四边形,则AC与BD互相平分;
④若四边形EFGH是正方形,则AC与BD互相垂直且相等.
其中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题
11.(2022春·新疆克拉玛依·八年级统考期末)已知平行四边形ABCD中,∠B+∠D=270°,则∠C=________.
12.(2022春·新疆塔城·八年级统考期末)如图,平行四边形ABCD的对角线AC与BD相交于点O,AB⊥AC.若AB=4,AC=6,则BD的长为_________.
13.(2022春·新疆巴音郭楞·八年级统考期末)如图,已知平面直角坐标系中的三点坐标分别为A(2,3),B(6,3),C(4,0).现要找到一点D,使得四个点构成的四边形是平行四边形,那么点D的坐标是________.
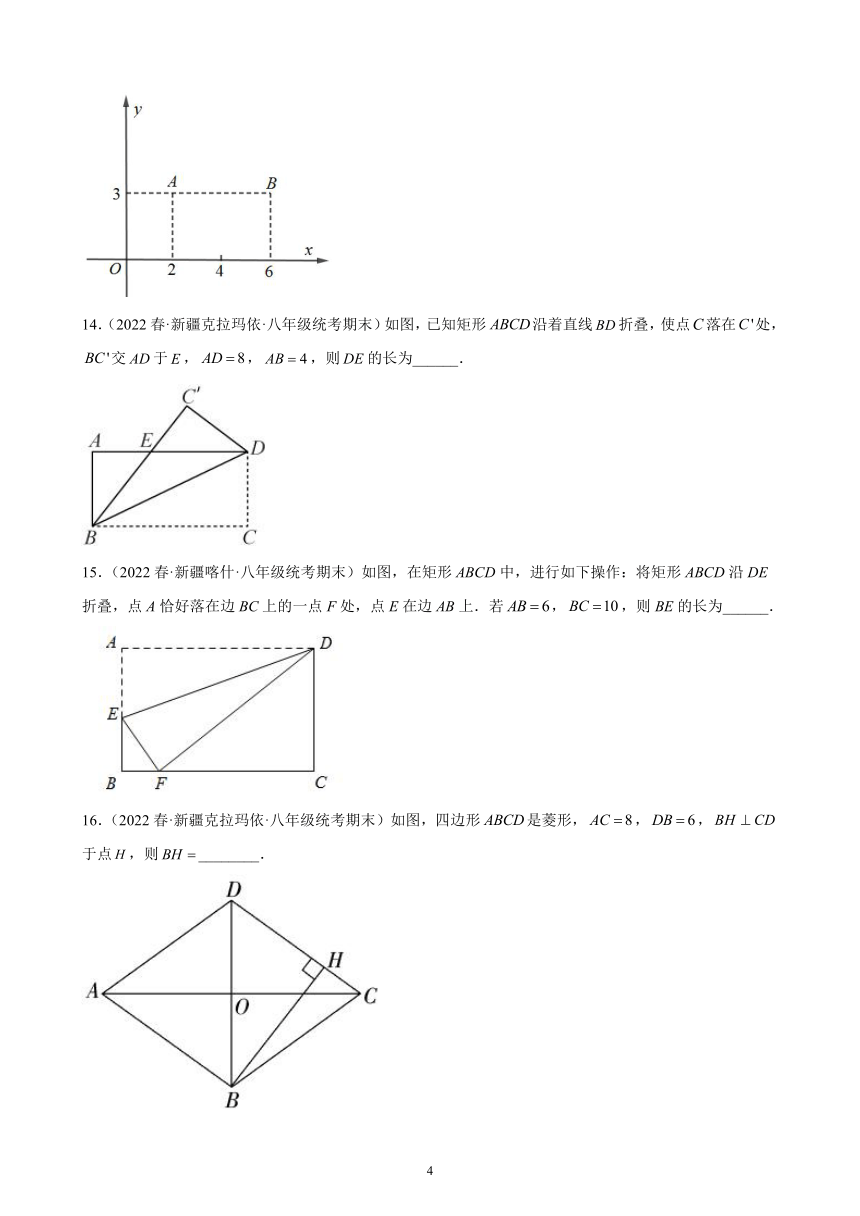
14.(2022春·新疆克拉玛依·八年级统考期末)如图,已知矩形沿着直线折叠,使点落在处,交于,,,则的长为______.
15.(2022春·新疆喀什·八年级统考期末)如图,在矩形ABCD中,进行如下操作:将矩形ABCD沿DE折叠,点A恰好落在边BC上的一点F处,点E在边AB上.若,,则BE的长为______.
16.(2022春·新疆克拉玛依·八年级统考期末)如图,四边形是菱形,,,于点,则________.
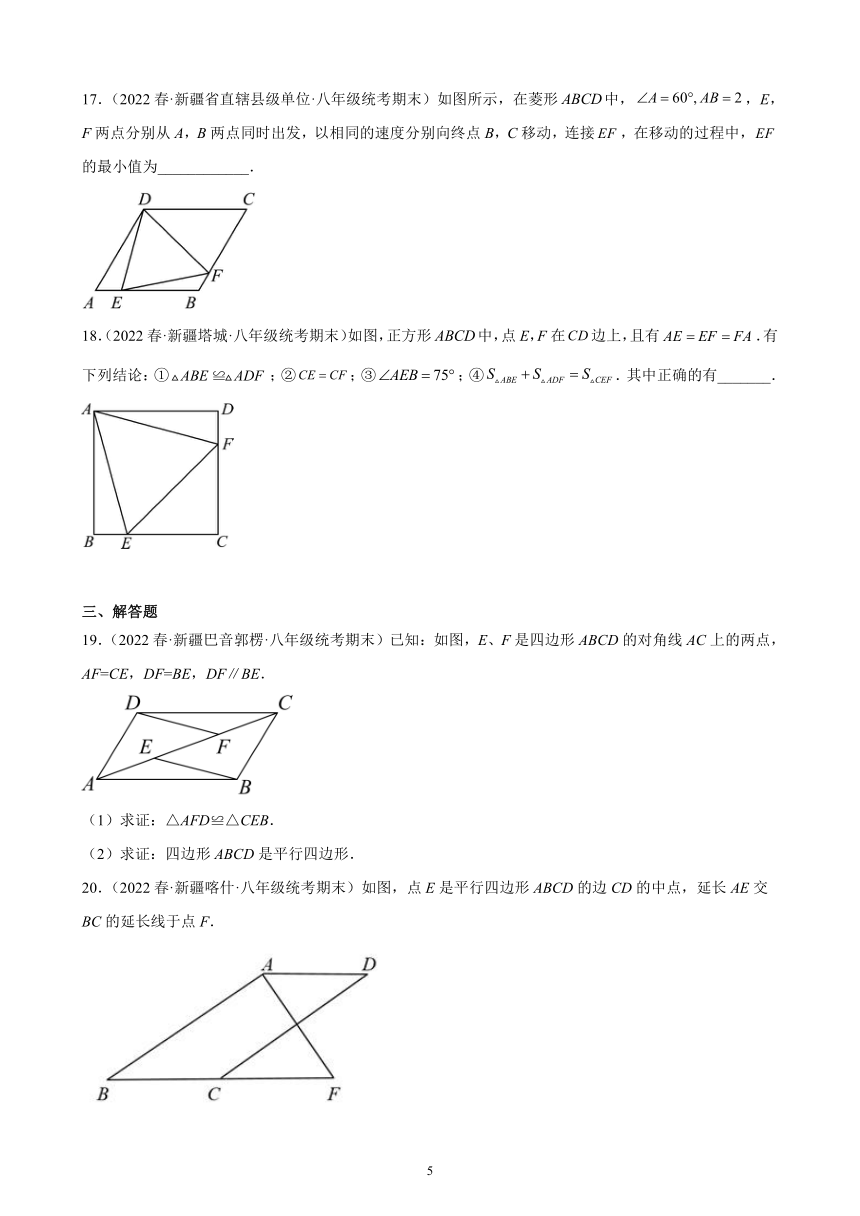
17.(2022春·新疆省直辖县级单位·八年级统考期末)如图所示,在菱形中,,E,F两点分别从A,B两点同时出发,以相同的速度分别向终点B,C移动,连接,在移动的过程中,的最小值为____________.
18.(2022春·新疆塔城·八年级统考期末)如图,正方形中,点E,F在边上,且有.有下列结论:①;②;③;④.其中正确的有_______.
三、解答题
19.(2022春·新疆巴音郭楞·八年级统考期末)已知:如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.
(1)求证:△AFD≌△CEB.
(2)求证:四边形ABCD是平行四边形.
20.(2022春·新疆喀什·八年级统考期末)如图,点E是平行四边形ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:;
(2)若,,,求CD的长.
21.(2022春·新疆巴音郭楞·八年级统考期末)如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
22.(2022春·新疆阿克苏·八年级统考期末)如图,在平行四边形中,过点D作于点E,点F在边上,,连接.
(1)求证:四边形是矩形;
(2)已知,是的平分线,若,求的长度.
23.(2022春·新疆喀什·八年级统考期末)如图,在中,,D是EC的中点,F是AD的中点,过点A作交EF的延长线于点B,连接BC.
(1)求证:;
(2)判断四边形ABCD的形状,并说明理由;
(3)若,,求四边形ABCD的面积.
24.(2022春·新疆克拉玛依·八年级统考期末)如图,菱形ABCD对角线交于点O,BE∥AC,AE∥BD,EO与AB交于点F.
(1)试判断四边形AEBO的形状,并说明你的理由;(2)求证:EO=DC.
25.(2022春·新疆乌鲁木齐·八年级统考期末)如图1,在 ABCD中,AB=14,AD=8,∠DAB=60°,对角线AC,BD交于点O.一动点P在边AB上由A向B运动(不与A,B重合),连接PO并延长,交CD于点Q.
(1)求证:OP=OQ;
(2)当AP=9时,求线段OP的长度;
(3)连接AQ,PC,如图2,随着点P的运动,四边形APCQ可能是菱形吗?如果可能,请求出此时线段AP的长度;如果不可能,请说明理由.
26.(2022春·新疆塔城·八年级统考期末)以四边形的边,为边分别向外侧作等边和等边,连接,,交点为G.
(1)当四边形为正方形时(如图1),直接说出和有什么数量关系.
(2)当四边形为矩形时(如图2),和具有怎样的数量关系?请加以证明;
(3)四边形由正方形到矩形到一般平行四边形的变化过程中,是否发生变化?如果改变,请说明理由;如果不变,请在图3中求出的度数.
27.(2022春·新疆克拉玛依·八年级统考期末)如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
(1)用含t的代数式表示:AP=________ cm;DP=________ cm;BQ=________ cm;CQ=________ cm.
(2)当t为何值时,四边形APQB是平行四边形?
(3)当t为何值时,四边形PDCQ是平行四边形?
参考答案:
1.B
【分析】直接利用平行四边形的性质得出AO=CO,BO=DO,DC=AB=6,再利用已知求出AO+BO的长,进而得出答案.
【详解】解:∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,DC=AB=6,
∵AC+BD=16,
∴AO+BO=8,
∴△ABO的周长是:14.
故选B.
【点睛】平行四边形的性质掌握要熟练,找到等值代换即可求解.
2.C
【详解】∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵AB=6,且AB的长是四边形ABCD周长的 ,
∴四边形ABCD周长为:6÷=32,
∴AB+BC=×32=16,
∴BC=10.
故选C.
3.B
【分析】根据平行四边形的判定方法,对每个选项进行筛选可得答案.
【详解】A、∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形,故A选项不符合题意;
B、AB=CD,AO=CO不能证明四边形ABCD是平行四边形,故本选项符合题意;
C、∵AD//BC,AD=BC,
∴四边形ABCD是平行四边形,故C选项不符合题意;
D、∵AB∥CD,
∴∠ABC+∠BCD=180°,∠BAD+∠ADC=180°,
又∵∠BAD=∠BCD,
∴∠ABC=∠ADC,
∵∠BAD=∠BCD,∠ABC=∠ADC,
∴四边形ABCD是平行四边形,故D选项不符合题意,
故选B.
【点睛】本题主要考查平行四边形的判定问题,熟练掌握平行四边形的性质,能够熟练判定一个四边形是否为平行四边形.
平行四边形的判定:①两组对边分别平行的四边形是平行四边形;②两组对边分别相等的四边形是平行四边形;③两组对角分别相等的四边形是平行四边形;④对角线互相平分的四边形是平行四边形;⑤一组对边平行且相等的四边形是平行四边形.
4.D
【分析】先利用互余计算出∠BDE=28°,再根据平行线的性质得∠CBD=∠BDE=28°,接着根据折叠的性质得∠FBD=∠CBD=28°,然后利用三角形外角性质计算∠DEF的度数,于是得到结论.
【详解】解:∵四边形ABCD为矩形,
∴AD∥BC,∠ADC=90°,
∵,
∵AD∥BC,
∴∠CBD=∠BDE=28°,
∵矩形ABCD沿对角线BD折叠,
∴∠FBD=∠CBD=28°,
∴∠DEF=∠FBD+∠BDE=28°+28°=56°.
故选:D.
【点睛】本题考查了矩形的性质,平行线和折叠的性质,综合运用以上性质是解题的关键.
5.A
【分析】由DE是的中位线,可得AC=12,在中,点F为AC中点,可得BF=即可.
【详解】解:∵DE是的中位线,
∴AC=2DE=2×6=12,
∵在中,,点F为AC中点,
∴BF=,
故选择A.
【点睛】本题考查三角形中位线与三角形中线性质,掌握三角形中位线与三角形中线性质是解题关键.
6.D
【分析】直接根据菱形的面积公式即可得出结论.
【详解】解:∵菱形ABCD中,AC=8,BD=6,
∴菱形的面积=AC BD=×8×6=24,故D正确.
故选:D.
【点睛】本题主要考查的是菱形的性质,熟知菱形面积等于对角线面积的一半是解答此题的关键.
7.D
【分析】连接AC、BD交于点O,根据题意可得BD=30cm,再由菱形的性质可得BO=5cm,AC⊥BD,然后根据勾股定理可得AO=12cm,即可求解.
【详解】解:如图,连接AC、BD交于点O,
∵BD间的距离是30cm,木制活动衣帽架是由三个全等的菱形构成,
∴BE=10cm,
∵四边形ABCE是菱形,
∴BO=EO,AO=CO,AC⊥BE,
∴BO=5cm,
∵菱形的边长AB=13cm,
在Rt△ABO中,
,
∴AC=24cm.
故选:D.
【点睛】本题主要考查了菱形的性质,勾股定理,熟练掌握菱形的性质,勾股定理是解题的关键.
8.A
【详解】设对角线的交点为O,∵四边形ABCD是菱形,AC=8,BD=6,∴∠AOD=90°,AO=4,DO=3,∴,∴周长为5×4=20,故选A.
9.A
【分析】根据特殊四边形的判定方法进行判断.
【详解】解:对角线互相平分的四边形是平行四边形,故选项A符合题意;
对角线相等的平行四边形是矩形,故选项B不符合题意;
对角线互相垂直的平行四边形是菱形,故选项C不符合题意;
对角线互相垂直且相等的平行四边形是正方形,故选项D不符合题意.
故选:A.
10.A
【分析】①由菱形的判定定理即可判断;②由矩形的判定定理,即可判断;③若四边形EFGH是平行四边形,与AC、BD是否互相平分无任何关系;④根据中位线性质解题.
【详解】解:由题意得:四边形EFGH平行四边形,
①若AC=BD,则四边形EFGH是菱形,故①错误;
②若AC⊥BD,则四边形EFGH是矩形,故②错误;
③若四边形EFGH是平行四边形,不能判定AC、BD是否互相平分,故③错误;
④点E、F、G、H分别是四边形ABCD边AB、BC、CD、DA的中点
若四边形EFGH是正方形,
AC与BD互相垂直且相等,故④正确.
故选:A.
【点睛】本题考查矩形、正方形、菱形等特殊四边形的判定与性质,是重要考点,难度较易,掌握相关知识是解题关键.
11.45°
【详解】试题解析:∵四边形ABCD为平行四边形,
∴AD∥BC,∠B=∠D,
且
故答案为
点睛:平行四边形的对角相等,邻角互补.
12.10
【详解】解:∵ABCD的对角线AC与BD相交于点O,AC=6,
∴BO=DO,AO=CO=3,
∵AB⊥AC,AB=4,
∴BO==5,
∴BD=2BO=10,
故答案为10.
13.(0,0)或(4,6)或(8,0)
【分析】分CD∥AB与AD∥BC两种情况讨论,利用平行四边形的性质结合坐标系特点即可完成.
【详解】由题意知AB=4.
当CD∥AB时,可求得D点坐标为(0,0)或(8,0).
当AD∥BC时,D点的坐标为(4,6)或(0,0).
综上得:点D的坐标为(0,0)或(4,6)或(8,0).
故答案为:(0,0)或(4,6)或(8,0).
【点睛】本题考查了坐标与图形,平行四边形的性质,注意分类讨论.
14.
【分析】首先根据矩形的性质可得出,即,然后根据折叠知,可得到,进而得出,设,则,利用勾股定理求出x的值,即可求出DE的长.
【详解】如图:
∵四边形ABCD是矩形,
∴,即,
由折叠知,,
∴,
∴,
设,则,
在中,,
∴,
解得:,
∴DE的长为5.
故答案为:5.
【点睛】本题主要考查折叠变换的知识点,解答本题的关键是掌握矩形的性质,勾股定理的利用以及折叠的知识,此题比较简单.
15.
【分析】先根据翻折变换的性质得出DF=AD=10,AE=FE,在Rt△CDF中利用勾股定理求出CF的长,进而求出BF的长, 在Rt△BEF中,利用勾股定理得出,即可求解.
【详解】解∶∵四边形ABCD是矩形,BC=10,AB=6,
∴AD=BC=10,CD=AB=6,∠B=90°,
∵将矩形ABCD沿DE折叠,点A恰好落在边BC上的一点F处,
∴AE=EF,DF=AD=10,
在Rt△CDF中,利用勾股定理得,
∴BF=BC-CF=2,
在Rt△BEF中, 由勾股定理得出,
∴,
∴.
故答案为∶.
【点睛】此题考查了折叠的性质、矩形的性质、勾股定理等知识.此题难度适中,注意掌握折叠前后图形的对应关系,注意数形结合思想的应用.
16.
【分析】首先根据菱形的性质,得出,的长,然后再根据勾股定理,得出的长,再利用菱形的面积,即可得出的长.
【详解】解:∵四边形是菱形,
∴,,
又∵,
∴,
∴,
∵,
∴,
解得:.
故答案为:
【点睛】本题主要考查了菱形的性质,勾股定理,解本题的关键在于能够熟练掌握菱形的性质.
17.
【分析】连接DB,作DH⊥AB于H,如图,利用菱形的性质得AD=AB=BC=CD,则可判断△ABD和△BCD都是等边三角形,再证明△ADE≌△BDF得到∠2=∠1,DE=DF,接着判定△DEF为等边三角形,所以EF=DE,然后根据垂线段最短判断DE的最小值即可.
【详解】解:连接DB,作DH⊥AB于H,如图,
∵四边形ABCD为菱形,
∴AD=AB=BC=CD,
而∠A=60°,
∴△ABD和△BCD都是等边三角形,
∴∠ADB=∠DBC=60°,AD=BD,
在Rt△ADH中,AH=1,AD=2,
∴DH==,
在△ADE和△BDF中,
∴△ADE≌△BDF,
∴∠2=∠1,DE=DF,
∴∠1+∠BDE=∠2+∠BDE=∠EDF=60°,
∴△DEF为等边三角形,
∴EF=DE,
而当E点运动到H点时,DE的值最小,其最小值为,
∴EF的最小值为,
故答案为:.
【点睛】本题考查了菱形的性质,等边三角形的判定与性质,全等三角形的判定和性质,添加恰当辅助线构造全等三角形是本题的关键.
18.①②③④
【分析】利用HL可证得,故①正确;再根据全等三角形的性质可得CE=CF,故②正确;然后根据△AEF是等边三角形,可得∠EAF=60°,,从而得到∠DAF=∠BAE=15°,故③正确;在AD上取点G是AG=GF,可得∠DGF=30°,设DF=x,则AG=FG=2x,可得,从而得到,,再求出和,可得④正确,即可求解.
【详解】解:在正方形中,∠B=∠D=∠C=∠BAD=90°,AB=AD=BC=CD,
∵AE=AF,
∴,故①正确;
∴BE=DF,
∴BC-BE=CD-DF,即CE=CF,故②正确;
∵,
∴△AEF是等边三角形,
∴∠EAF=60°,
∴∠BAE+∠DAF=30°,
∵,
∴∠BAE=∠DAF,
∴∠DAF=∠BAE=15°,
∴∠AEB=90°-∠BAE=75°,故③正确;
如图,在AD上取点G使AG=GF,
∴∠AFG=∠DAF=15°,
∴∠DGF=30°,
设DF=x,则AG=FG=2x,
∴,
∴,
∴,
∵,
∴,
∴,
,
∴,故④正确;
故答案为:①②③④
【点睛】本题主要考查了正方形的性质,全等三角形的判定和性质,勾股定理,直角三角形的性质,等边三角形的性质,熟练掌握正方形的性质,全等三角形的判定和性质,勾股定理,直角三角形的性质,等边三角形的性质是解题的关键.
19.证明见解析
【分析】(1)利用两边和它们的夹角对应相等的两三角形全等(SAS),这一判定定理容易证明△AFD≌△CEB.
(2)由△AFD≌△CEB,容易证明AD=BC且AD//BC,可根据一组对边平行且相等的四边形是平行四边形.
【详解】证明:(1)∵DF∥BE,
∴∠DFE=∠BEF.
又∵AF=CE,DF=BE,
∴△AFD≌△CEB(SAS).
(2)由(1)知△AFD≌△CEB,
∴∠DAC=∠BCA,AD=BC,
∴AD∥BC.
∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形).
【点睛】本题考查全等三角形的判定与性质及平行四边形的判定,熟练掌握判定定理是解题关键.
20.(1)见解析
(2)16
【分析】(1)要证明即可证明;
(2)根据(1)中的结论和勾股定理、平行四边形的性质可以求得的长.
【详解】(1)明:∵四边形ABCD是平行四边形,
∴,
∴ ,
∵E是CD的中点,
∴,
在和中
∴(ASA),
∴;
(2)解:∵四边形ABCD是平行四边形,
∴,,
∴,
∵,
∴,
∴是直角三角形,
∵,,,
∴,
∵,
在中,由勾股定理得,
∵,
∴,
∴.
【点睛】本题主要考查全等三角形的判定与性质,平行四边形性质、勾股定理,掌握定理以及性质是解题的关键.
21.(1)见解析;(2)6.5.(3)当点O在边AC上运动到AC中点时,四边形AECF是矩形.理由见详解;
【分析】(1)根据平行线的性质以及角平分线的性质得出∠1=∠2,∠3=∠4,进而得出答案.
(2)根据已知得出∠2+∠4=∠5+∠6=90°,进而利用勾股定理求出EF的长,即可根据直角三角形斜边上的中线性质得出CO的长.
(3)根据平行四边形的判定以及矩形的判定得出即可.
【详解】解:(1)证明:如图,∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,4=∠6.
∵MN∥BC,
∴∠1=∠5,3=∠6.
∴∠1=∠2,∠3=∠4.
∴EO=CO,FO=CO.
∴OE=OF.
(2)∵∠2=∠5,∠4=∠6,
∴∠2+∠4=∠5+∠6=90°.
∵CE=12,CF=5,
∴.
∴OC=EF=6.5.
(3)当点O在边AC上运动到AC中点时,四边形AECF是矩形.理由如下:
当O为AC的中点时,AO=CO,
∵EO=FO,
∴四边形AECF是平行四边形.
∵∠ECF=90°,
∴平行四边形AECF是矩形.
22.(1)证明见解析
(2)
【分析】(1)先由平行四边形的性质得到,再证明即可证明四边形是平行四边形,又,即可证明平行四边形是矩形;
(2)先根据含30度角的直角三角形的性质求出的长,再证明是等腰三角形,求出的长,由此即可得到答案.
【详解】(1)证明:∵四边形是平行四边形,
∴,
∵,
∴,
∴四边形是平行四边形,
又∵,
∴平行四边形是矩形;
(2)解:在中,,
∴,
∴,
∵,
∴,
∵是的平分线,
∴,
∴,
∴,
∴.
【点睛】本题主要考查了平行四边形的性质与判定,矩形的判定,含30度角的直角三角形的性质,灵活运用所学知识是解题的关键.
23.(1)见解析
(2)菱形,理由见解析
(3)24
【分析】(1)根据两直线平行,内错角相等及中点的定义得出,,即可证明三角形全等;
(2)由全等三角形的性质及中点定义,结合已知即可得出四边形ABCD是平行四边形,再根据直角三角形斜边中线等于斜边的一半,即可证明;
(3)先利用勾股定理求出,再根据直角三角形斜边中线等于斜边的一半求出,连接BD交AC于点O,利用菱形的性质和勾股定理即可求解.
(1)
∵,
∴.
∵F是AD的中点,
∴.
又∵,
∴.
(2)
四边形ABCD是菱形.
理由如下:∵,
∴.
∵D是EC的中点,
∴,
∴.
又∵,
∴四边形ABCD是平行四边形.
∵D是EC的中点,
∴AD是斜边上的中线,
∴,
∴平行四边形ABCD是菱形.
(3)
∵,,
∴在中,由勾股定理得:,
∵AD是直角斜边上的中线,
∴.
连接BD交AC于点O,
∴在菱形中,,,
∴在中,由勾股定理得,
∴,
∴.
【点睛】本题考查了平行线的性质,中点的定义,全等三角形的判定和性质,直角三角形斜边中线等于斜边的一半,菱形的判定和性质,勾股定理,熟练掌握知识点是解题的关键.
24.证明见解析
【分析】(1)由菱形的性质可证明∠BOA=90°,然后再证明四边形AEBO为平行四边形,从而可证明四边形AEBO是矩形;
(2)依据矩形的性质可得到EO=BA,然后依据菱形的性质可得到AB=CD.
【详解】(1)四边形AEBO是矩形.
证明:∵BE∥AC,AE∥BD,
∴四边形AEBO是平行四边形.
又∵菱形ABCD对角线交于点O,
∴AC⊥BD,即∠AOB=90°.
∴四边形AEBO是矩形.
(2)∵四边形AEBO是矩形,
∴EO=AB,
在菱形ABCD中,AB=DC.
∴EO=DC.
【点睛】本题主要考查的是菱形的性质判定、矩形的性质和判定,熟练掌握相关图形的性质是解题的关键.
25.(1)见解析;(2);(3)有可能,AP=.
【分析】(1)先根据平行四边形的性质证得△AOP≌△COQ,再运用全等三角形的性质即可证明;
(2)如图(2):过D作DE⊥AB,垂足为E,再根据直角三角形的性质求得AE=4,进而求得DE=,然后再说明OP为△DBE的中位线,最后根据中位线的性质即可解答;
(3)如图(3):过C作CF⊥AB交AB延长线于F,先说明四边形APCQ为平行四边形,当四边形APCQ为菱形时有AP=PC,然后在Rt△PCF中运用勾股定理解答即可.
【详解】(1)证明:∵平行四边形ABCD
∴CD//AB,OA=OC,OB=OD
∴∠DCA=∠BAC,∠CQP=∠APQ
∴△AOP≌△COQ(AAS)
∴OP=OQ;
(2)如图(2):过D作DE⊥AB,垂足为E
∵∠DAB=60°
∴AE=AD=4
∴DE=
∴BE=AB-AE=14-4=10,PE=AP-AE=9-4 =5,PB=AB-AP=5
∴PE=PB
∵OB=OD
∴OP为△DBE的中位线
∴OP=DE=;
(3)有可能,理由如下:
如图(3):过C作CF⊥AB交AB延长线于F
∵平行四边形ABCD
∴BC//AD,BC=AD
∴∠CBF=∠DAB=60°
∴BF=BC=4
∴CF=
∵OP=OQ,OA=OC
∴四边形APCQ为平行四边形
当四边形APCQ为菱形时,则需AP=CP
∵PF=AB+BF-AP=18-AP
∴在Rt△PCF中,PC2=FC2+PF2
∴AP2=()2+(18-AP)2,解得AP=.
【点睛】本题主要考查了平行四边形的性质、菱形的判定、全等三角形的判定与性质以及勾股定理等知识点,灵活应用相关性质、判定定理成为解答本题的关键.
26.(1)EB=FD
(2)EB=FD,证明见解析;
(3)∠EGD不发生变化,仍然是60°.
【分析】(1)根据等边三角形的性质可证,△AFD≌△ABE,则=;
(2)由(1)同理可证△AFD≌△ABE,从而得出EB=FD;
(3)由(2)同理得:△FAD≌△BAE,则∠AEB=∠ADF,再利用三角形内角和定理可得答案.
【详解】(1)解:EB=FD,理由如下:
∵△ADE、△ABF是等边三角形,
∴AE=AD,AB=AF,∠DAE=∠BAF,
∴∠BAE=∠DAF,
∴△AFD≌△ABE(SAS),
∴EB=FD,
(2)EB=FD,理由如下:
∵△AFB为等边三角形,
∴AF=AB,∠FAB=60,
∵△ADE为等边三角形,
∴AD=AE,∠EAD=60,
∴∠FAB+∠BAD=∠EAD+∠BAD,
即∠FAD=∠BAE,
∴△FAD≌△BAE(SAS),
∴EB=FD;
(3)不变,理由如下:
由(2)同理得:△FAD≌△BAE,
∴∠AEB=∠ADF,
设∠AEB为x,则∠ADF也为x,
于是有∠BED为(60-x),∠EDF为(60+x),
∴∠EGD=180-∠BED-∠EDF=180-(60-x)-(60+x)=60.
【点睛】本题是四边形综合题,主要考查了正方形的性质,等边三角形的性质,全等三角形的判定与性质等知识,证明△FAD≌△BAE是解题的关键.
27.(1)t,(12﹣t),(15﹣2t),2t;(2)当t=5为何值时,四边形APQB是平行四边形;(3)当t=4时,四边形PDCQ是平行四边形
【分析】(1)根据速度、路程以及时间的关系和线段之间的数量关系,即可求出AP,DP,BQ,CQ的长;
(2)当AP=BQ时,四边形APQB是平行四边形,建立关于t的一元一次方程方程,解方程求出符合题意的t值即可;
(3)当PD=CQ时,四边形PDCQ是平行四边形;建立关于t的一元一次方程方程,解方程求出符合题意的t值即可.
【详解】解:(1)t,(12﹣t),(15﹣2t),2t;
(2)根据题意有AP=t,CQ=2t,PD=12﹣t,BQ=15﹣2t.
∵AD∥BC,
∴当AP=BQ时,四边形APQB是平行四边形.
∴t=15﹣2t,
解得t=5.
∴t=5时四边形APQB是平行四边形;
(3)由AP=tcm,CQ=2tcm,
∵AD=12cm,BC=15cm,
∴PD=AD﹣AP=12﹣t,
如图1,∵AD∥BC,
∴当PD=QC时,四边形PDCQ是平行四边形.
即:12﹣t=2t,
解得t=4,
∴当t=4时,四边形PDCQ是平行四边形.
【点睛】本题考查了平行四边形的判定和性质的应用,题目是一道综合性比较强的题目,难度适中,解题的关键是把握“化动为静”的解题思想.
一、单选题
1.(2022春·新疆克拉玛依·八年级统考期末)如图, ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )
A.10 B.14 C.20 D.22
2.(2022春·新疆塔城·八年级统考期末)如果四边形ABCD是平行四边形,AB=6,且AB的长是四边形ABCD周长的,那么BC的长是( )
A.6 B.8 C.10 D.16
3.(2022春·新疆克拉玛依·八年级统考期末)如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A., B.,
C., D.,
4.(2022春·新疆阿克苏·八年级统考期末)如图,将矩形ABCD沿对角线BD折叠,使点C落在F处,BF交AD于点E.若∠BDC=62°,则∠DEF的度数为( )
A.31° B.28° C.62° D.56°
5.(2022春·新疆塔城·八年级统考期末)如图,在中,,点F为AC中点,是的中位线,若,则BF=( )
A.6 B.4 C.3 D.5
6.(2022春·新疆巴音郭楞·八年级统考期末)如图,菱形中,,,则菱形的面积为( )
A.20 B.40 C.28 D.24
7.(2022春·新疆塔城·八年级统考期末)如图,一个木制的活动衣帽架由3个全等的菱形构成.已知菱形的边长为,当挂钩B、D间的距离是时,则挂钩A、C间的距离是( ).
A. B. C.12 D.24
8.(2022春·新疆和田·八年级统考期末)如图,菱形ABCD中,AC=8,BD=6,则菱形的周长是( )
A.20 B.24
C.28 D.40
9.(2022春·新疆喀什·八年级统考期末)下列命题中,是真命题的是( )
A.两条对角线互相平分的四边形是平行四边形
B.两条对角线相等的四边形是矩形
C.两条对角线互相垂直的四边形是菱形
D.两条对角线互相垂直且相等的四边形是正方形
10.(2022春·新疆克拉玛依·八年级统考期末)如图,点E、F、G、H分别是四边形ABCD边AB、BC、CD、DA的中点.则下列说法:
①若AC=BD,则四边形EFGH为矩形;
②若AC⊥BD,则四边形EFGH为菱形;
③若四边形EFGH是平行四边形,则AC与BD互相平分;
④若四边形EFGH是正方形,则AC与BD互相垂直且相等.
其中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题
11.(2022春·新疆克拉玛依·八年级统考期末)已知平行四边形ABCD中,∠B+∠D=270°,则∠C=________.
12.(2022春·新疆塔城·八年级统考期末)如图,平行四边形ABCD的对角线AC与BD相交于点O,AB⊥AC.若AB=4,AC=6,则BD的长为_________.
13.(2022春·新疆巴音郭楞·八年级统考期末)如图,已知平面直角坐标系中的三点坐标分别为A(2,3),B(6,3),C(4,0).现要找到一点D,使得四个点构成的四边形是平行四边形,那么点D的坐标是________.
14.(2022春·新疆克拉玛依·八年级统考期末)如图,已知矩形沿着直线折叠,使点落在处,交于,,,则的长为______.
15.(2022春·新疆喀什·八年级统考期末)如图,在矩形ABCD中,进行如下操作:将矩形ABCD沿DE折叠,点A恰好落在边BC上的一点F处,点E在边AB上.若,,则BE的长为______.
16.(2022春·新疆克拉玛依·八年级统考期末)如图,四边形是菱形,,,于点,则________.
17.(2022春·新疆省直辖县级单位·八年级统考期末)如图所示,在菱形中,,E,F两点分别从A,B两点同时出发,以相同的速度分别向终点B,C移动,连接,在移动的过程中,的最小值为____________.
18.(2022春·新疆塔城·八年级统考期末)如图,正方形中,点E,F在边上,且有.有下列结论:①;②;③;④.其中正确的有_______.
三、解答题
19.(2022春·新疆巴音郭楞·八年级统考期末)已知:如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.
(1)求证:△AFD≌△CEB.
(2)求证:四边形ABCD是平行四边形.
20.(2022春·新疆喀什·八年级统考期末)如图,点E是平行四边形ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:;
(2)若,,,求CD的长.
21.(2022春·新疆巴音郭楞·八年级统考期末)如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
22.(2022春·新疆阿克苏·八年级统考期末)如图,在平行四边形中,过点D作于点E,点F在边上,,连接.
(1)求证:四边形是矩形;
(2)已知,是的平分线,若,求的长度.
23.(2022春·新疆喀什·八年级统考期末)如图,在中,,D是EC的中点,F是AD的中点,过点A作交EF的延长线于点B,连接BC.
(1)求证:;
(2)判断四边形ABCD的形状,并说明理由;
(3)若,,求四边形ABCD的面积.
24.(2022春·新疆克拉玛依·八年级统考期末)如图,菱形ABCD对角线交于点O,BE∥AC,AE∥BD,EO与AB交于点F.
(1)试判断四边形AEBO的形状,并说明你的理由;(2)求证:EO=DC.
25.(2022春·新疆乌鲁木齐·八年级统考期末)如图1,在 ABCD中,AB=14,AD=8,∠DAB=60°,对角线AC,BD交于点O.一动点P在边AB上由A向B运动(不与A,B重合),连接PO并延长,交CD于点Q.
(1)求证:OP=OQ;
(2)当AP=9时,求线段OP的长度;
(3)连接AQ,PC,如图2,随着点P的运动,四边形APCQ可能是菱形吗?如果可能,请求出此时线段AP的长度;如果不可能,请说明理由.
26.(2022春·新疆塔城·八年级统考期末)以四边形的边,为边分别向外侧作等边和等边,连接,,交点为G.
(1)当四边形为正方形时(如图1),直接说出和有什么数量关系.
(2)当四边形为矩形时(如图2),和具有怎样的数量关系?请加以证明;
(3)四边形由正方形到矩形到一般平行四边形的变化过程中,是否发生变化?如果改变,请说明理由;如果不变,请在图3中求出的度数.
27.(2022春·新疆克拉玛依·八年级统考期末)如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
(1)用含t的代数式表示:AP=________ cm;DP=________ cm;BQ=________ cm;CQ=________ cm.
(2)当t为何值时,四边形APQB是平行四边形?
(3)当t为何值时,四边形PDCQ是平行四边形?
参考答案:
1.B
【分析】直接利用平行四边形的性质得出AO=CO,BO=DO,DC=AB=6,再利用已知求出AO+BO的长,进而得出答案.
【详解】解:∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,DC=AB=6,
∵AC+BD=16,
∴AO+BO=8,
∴△ABO的周长是:14.
故选B.
【点睛】平行四边形的性质掌握要熟练,找到等值代换即可求解.
2.C
【详解】∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵AB=6,且AB的长是四边形ABCD周长的 ,
∴四边形ABCD周长为:6÷=32,
∴AB+BC=×32=16,
∴BC=10.
故选C.
3.B
【分析】根据平行四边形的判定方法,对每个选项进行筛选可得答案.
【详解】A、∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形,故A选项不符合题意;
B、AB=CD,AO=CO不能证明四边形ABCD是平行四边形,故本选项符合题意;
C、∵AD//BC,AD=BC,
∴四边形ABCD是平行四边形,故C选项不符合题意;
D、∵AB∥CD,
∴∠ABC+∠BCD=180°,∠BAD+∠ADC=180°,
又∵∠BAD=∠BCD,
∴∠ABC=∠ADC,
∵∠BAD=∠BCD,∠ABC=∠ADC,
∴四边形ABCD是平行四边形,故D选项不符合题意,
故选B.
【点睛】本题主要考查平行四边形的判定问题,熟练掌握平行四边形的性质,能够熟练判定一个四边形是否为平行四边形.
平行四边形的判定:①两组对边分别平行的四边形是平行四边形;②两组对边分别相等的四边形是平行四边形;③两组对角分别相等的四边形是平行四边形;④对角线互相平分的四边形是平行四边形;⑤一组对边平行且相等的四边形是平行四边形.
4.D
【分析】先利用互余计算出∠BDE=28°,再根据平行线的性质得∠CBD=∠BDE=28°,接着根据折叠的性质得∠FBD=∠CBD=28°,然后利用三角形外角性质计算∠DEF的度数,于是得到结论.
【详解】解:∵四边形ABCD为矩形,
∴AD∥BC,∠ADC=90°,
∵,
∵AD∥BC,
∴∠CBD=∠BDE=28°,
∵矩形ABCD沿对角线BD折叠,
∴∠FBD=∠CBD=28°,
∴∠DEF=∠FBD+∠BDE=28°+28°=56°.
故选:D.
【点睛】本题考查了矩形的性质,平行线和折叠的性质,综合运用以上性质是解题的关键.
5.A
【分析】由DE是的中位线,可得AC=12,在中,点F为AC中点,可得BF=即可.
【详解】解:∵DE是的中位线,
∴AC=2DE=2×6=12,
∵在中,,点F为AC中点,
∴BF=,
故选择A.
【点睛】本题考查三角形中位线与三角形中线性质,掌握三角形中位线与三角形中线性质是解题关键.
6.D
【分析】直接根据菱形的面积公式即可得出结论.
【详解】解:∵菱形ABCD中,AC=8,BD=6,
∴菱形的面积=AC BD=×8×6=24,故D正确.
故选:D.
【点睛】本题主要考查的是菱形的性质,熟知菱形面积等于对角线面积的一半是解答此题的关键.
7.D
【分析】连接AC、BD交于点O,根据题意可得BD=30cm,再由菱形的性质可得BO=5cm,AC⊥BD,然后根据勾股定理可得AO=12cm,即可求解.
【详解】解:如图,连接AC、BD交于点O,
∵BD间的距离是30cm,木制活动衣帽架是由三个全等的菱形构成,
∴BE=10cm,
∵四边形ABCE是菱形,
∴BO=EO,AO=CO,AC⊥BE,
∴BO=5cm,
∵菱形的边长AB=13cm,
在Rt△ABO中,
,
∴AC=24cm.
故选:D.
【点睛】本题主要考查了菱形的性质,勾股定理,熟练掌握菱形的性质,勾股定理是解题的关键.
8.A
【详解】设对角线的交点为O,∵四边形ABCD是菱形,AC=8,BD=6,∴∠AOD=90°,AO=4,DO=3,∴,∴周长为5×4=20,故选A.
9.A
【分析】根据特殊四边形的判定方法进行判断.
【详解】解:对角线互相平分的四边形是平行四边形,故选项A符合题意;
对角线相等的平行四边形是矩形,故选项B不符合题意;
对角线互相垂直的平行四边形是菱形,故选项C不符合题意;
对角线互相垂直且相等的平行四边形是正方形,故选项D不符合题意.
故选:A.
10.A
【分析】①由菱形的判定定理即可判断;②由矩形的判定定理,即可判断;③若四边形EFGH是平行四边形,与AC、BD是否互相平分无任何关系;④根据中位线性质解题.
【详解】解:由题意得:四边形EFGH平行四边形,
①若AC=BD,则四边形EFGH是菱形,故①错误;
②若AC⊥BD,则四边形EFGH是矩形,故②错误;
③若四边形EFGH是平行四边形,不能判定AC、BD是否互相平分,故③错误;
④点E、F、G、H分别是四边形ABCD边AB、BC、CD、DA的中点
若四边形EFGH是正方形,
AC与BD互相垂直且相等,故④正确.
故选:A.
【点睛】本题考查矩形、正方形、菱形等特殊四边形的判定与性质,是重要考点,难度较易,掌握相关知识是解题关键.
11.45°
【详解】试题解析:∵四边形ABCD为平行四边形,
∴AD∥BC,∠B=∠D,
且
故答案为
点睛:平行四边形的对角相等,邻角互补.
12.10
【详解】解:∵ABCD的对角线AC与BD相交于点O,AC=6,
∴BO=DO,AO=CO=3,
∵AB⊥AC,AB=4,
∴BO==5,
∴BD=2BO=10,
故答案为10.
13.(0,0)或(4,6)或(8,0)
【分析】分CD∥AB与AD∥BC两种情况讨论,利用平行四边形的性质结合坐标系特点即可完成.
【详解】由题意知AB=4.
当CD∥AB时,可求得D点坐标为(0,0)或(8,0).
当AD∥BC时,D点的坐标为(4,6)或(0,0).
综上得:点D的坐标为(0,0)或(4,6)或(8,0).
故答案为:(0,0)或(4,6)或(8,0).
【点睛】本题考查了坐标与图形,平行四边形的性质,注意分类讨论.
14.
【分析】首先根据矩形的性质可得出,即,然后根据折叠知,可得到,进而得出,设,则,利用勾股定理求出x的值,即可求出DE的长.
【详解】如图:
∵四边形ABCD是矩形,
∴,即,
由折叠知,,
∴,
∴,
设,则,
在中,,
∴,
解得:,
∴DE的长为5.
故答案为:5.
【点睛】本题主要考查折叠变换的知识点,解答本题的关键是掌握矩形的性质,勾股定理的利用以及折叠的知识,此题比较简单.
15.
【分析】先根据翻折变换的性质得出DF=AD=10,AE=FE,在Rt△CDF中利用勾股定理求出CF的长,进而求出BF的长, 在Rt△BEF中,利用勾股定理得出,即可求解.
【详解】解∶∵四边形ABCD是矩形,BC=10,AB=6,
∴AD=BC=10,CD=AB=6,∠B=90°,
∵将矩形ABCD沿DE折叠,点A恰好落在边BC上的一点F处,
∴AE=EF,DF=AD=10,
在Rt△CDF中,利用勾股定理得,
∴BF=BC-CF=2,
在Rt△BEF中, 由勾股定理得出,
∴,
∴.
故答案为∶.
【点睛】此题考查了折叠的性质、矩形的性质、勾股定理等知识.此题难度适中,注意掌握折叠前后图形的对应关系,注意数形结合思想的应用.
16.
【分析】首先根据菱形的性质,得出,的长,然后再根据勾股定理,得出的长,再利用菱形的面积,即可得出的长.
【详解】解:∵四边形是菱形,
∴,,
又∵,
∴,
∴,
∵,
∴,
解得:.
故答案为:
【点睛】本题主要考查了菱形的性质,勾股定理,解本题的关键在于能够熟练掌握菱形的性质.
17.
【分析】连接DB,作DH⊥AB于H,如图,利用菱形的性质得AD=AB=BC=CD,则可判断△ABD和△BCD都是等边三角形,再证明△ADE≌△BDF得到∠2=∠1,DE=DF,接着判定△DEF为等边三角形,所以EF=DE,然后根据垂线段最短判断DE的最小值即可.
【详解】解:连接DB,作DH⊥AB于H,如图,
∵四边形ABCD为菱形,
∴AD=AB=BC=CD,
而∠A=60°,
∴△ABD和△BCD都是等边三角形,
∴∠ADB=∠DBC=60°,AD=BD,
在Rt△ADH中,AH=1,AD=2,
∴DH==,
在△ADE和△BDF中,
∴△ADE≌△BDF,
∴∠2=∠1,DE=DF,
∴∠1+∠BDE=∠2+∠BDE=∠EDF=60°,
∴△DEF为等边三角形,
∴EF=DE,
而当E点运动到H点时,DE的值最小,其最小值为,
∴EF的最小值为,
故答案为:.
【点睛】本题考查了菱形的性质,等边三角形的判定与性质,全等三角形的判定和性质,添加恰当辅助线构造全等三角形是本题的关键.
18.①②③④
【分析】利用HL可证得,故①正确;再根据全等三角形的性质可得CE=CF,故②正确;然后根据△AEF是等边三角形,可得∠EAF=60°,,从而得到∠DAF=∠BAE=15°,故③正确;在AD上取点G是AG=GF,可得∠DGF=30°,设DF=x,则AG=FG=2x,可得,从而得到,,再求出和,可得④正确,即可求解.
【详解】解:在正方形中,∠B=∠D=∠C=∠BAD=90°,AB=AD=BC=CD,
∵AE=AF,
∴,故①正确;
∴BE=DF,
∴BC-BE=CD-DF,即CE=CF,故②正确;
∵,
∴△AEF是等边三角形,
∴∠EAF=60°,
∴∠BAE+∠DAF=30°,
∵,
∴∠BAE=∠DAF,
∴∠DAF=∠BAE=15°,
∴∠AEB=90°-∠BAE=75°,故③正确;
如图,在AD上取点G使AG=GF,
∴∠AFG=∠DAF=15°,
∴∠DGF=30°,
设DF=x,则AG=FG=2x,
∴,
∴,
∴,
∵,
∴,
∴,
,
∴,故④正确;
故答案为:①②③④
【点睛】本题主要考查了正方形的性质,全等三角形的判定和性质,勾股定理,直角三角形的性质,等边三角形的性质,熟练掌握正方形的性质,全等三角形的判定和性质,勾股定理,直角三角形的性质,等边三角形的性质是解题的关键.
19.证明见解析
【分析】(1)利用两边和它们的夹角对应相等的两三角形全等(SAS),这一判定定理容易证明△AFD≌△CEB.
(2)由△AFD≌△CEB,容易证明AD=BC且AD//BC,可根据一组对边平行且相等的四边形是平行四边形.
【详解】证明:(1)∵DF∥BE,
∴∠DFE=∠BEF.
又∵AF=CE,DF=BE,
∴△AFD≌△CEB(SAS).
(2)由(1)知△AFD≌△CEB,
∴∠DAC=∠BCA,AD=BC,
∴AD∥BC.
∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形).
【点睛】本题考查全等三角形的判定与性质及平行四边形的判定,熟练掌握判定定理是解题关键.
20.(1)见解析
(2)16
【分析】(1)要证明即可证明;
(2)根据(1)中的结论和勾股定理、平行四边形的性质可以求得的长.
【详解】(1)明:∵四边形ABCD是平行四边形,
∴,
∴ ,
∵E是CD的中点,
∴,
在和中
∴(ASA),
∴;
(2)解:∵四边形ABCD是平行四边形,
∴,,
∴,
∵,
∴,
∴是直角三角形,
∵,,,
∴,
∵,
在中,由勾股定理得,
∵,
∴,
∴.
【点睛】本题主要考查全等三角形的判定与性质,平行四边形性质、勾股定理,掌握定理以及性质是解题的关键.
21.(1)见解析;(2)6.5.(3)当点O在边AC上运动到AC中点时,四边形AECF是矩形.理由见详解;
【分析】(1)根据平行线的性质以及角平分线的性质得出∠1=∠2,∠3=∠4,进而得出答案.
(2)根据已知得出∠2+∠4=∠5+∠6=90°,进而利用勾股定理求出EF的长,即可根据直角三角形斜边上的中线性质得出CO的长.
(3)根据平行四边形的判定以及矩形的判定得出即可.
【详解】解:(1)证明:如图,∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,4=∠6.
∵MN∥BC,
∴∠1=∠5,3=∠6.
∴∠1=∠2,∠3=∠4.
∴EO=CO,FO=CO.
∴OE=OF.
(2)∵∠2=∠5,∠4=∠6,
∴∠2+∠4=∠5+∠6=90°.
∵CE=12,CF=5,
∴.
∴OC=EF=6.5.
(3)当点O在边AC上运动到AC中点时,四边形AECF是矩形.理由如下:
当O为AC的中点时,AO=CO,
∵EO=FO,
∴四边形AECF是平行四边形.
∵∠ECF=90°,
∴平行四边形AECF是矩形.
22.(1)证明见解析
(2)
【分析】(1)先由平行四边形的性质得到,再证明即可证明四边形是平行四边形,又,即可证明平行四边形是矩形;
(2)先根据含30度角的直角三角形的性质求出的长,再证明是等腰三角形,求出的长,由此即可得到答案.
【详解】(1)证明:∵四边形是平行四边形,
∴,
∵,
∴,
∴四边形是平行四边形,
又∵,
∴平行四边形是矩形;
(2)解:在中,,
∴,
∴,
∵,
∴,
∵是的平分线,
∴,
∴,
∴,
∴.
【点睛】本题主要考查了平行四边形的性质与判定,矩形的判定,含30度角的直角三角形的性质,灵活运用所学知识是解题的关键.
23.(1)见解析
(2)菱形,理由见解析
(3)24
【分析】(1)根据两直线平行,内错角相等及中点的定义得出,,即可证明三角形全等;
(2)由全等三角形的性质及中点定义,结合已知即可得出四边形ABCD是平行四边形,再根据直角三角形斜边中线等于斜边的一半,即可证明;
(3)先利用勾股定理求出,再根据直角三角形斜边中线等于斜边的一半求出,连接BD交AC于点O,利用菱形的性质和勾股定理即可求解.
(1)
∵,
∴.
∵F是AD的中点,
∴.
又∵,
∴.
(2)
四边形ABCD是菱形.
理由如下:∵,
∴.
∵D是EC的中点,
∴,
∴.
又∵,
∴四边形ABCD是平行四边形.
∵D是EC的中点,
∴AD是斜边上的中线,
∴,
∴平行四边形ABCD是菱形.
(3)
∵,,
∴在中,由勾股定理得:,
∵AD是直角斜边上的中线,
∴.
连接BD交AC于点O,
∴在菱形中,,,
∴在中,由勾股定理得,
∴,
∴.
【点睛】本题考查了平行线的性质,中点的定义,全等三角形的判定和性质,直角三角形斜边中线等于斜边的一半,菱形的判定和性质,勾股定理,熟练掌握知识点是解题的关键.
24.证明见解析
【分析】(1)由菱形的性质可证明∠BOA=90°,然后再证明四边形AEBO为平行四边形,从而可证明四边形AEBO是矩形;
(2)依据矩形的性质可得到EO=BA,然后依据菱形的性质可得到AB=CD.
【详解】(1)四边形AEBO是矩形.
证明:∵BE∥AC,AE∥BD,
∴四边形AEBO是平行四边形.
又∵菱形ABCD对角线交于点O,
∴AC⊥BD,即∠AOB=90°.
∴四边形AEBO是矩形.
(2)∵四边形AEBO是矩形,
∴EO=AB,
在菱形ABCD中,AB=DC.
∴EO=DC.
【点睛】本题主要考查的是菱形的性质判定、矩形的性质和判定,熟练掌握相关图形的性质是解题的关键.
25.(1)见解析;(2);(3)有可能,AP=.
【分析】(1)先根据平行四边形的性质证得△AOP≌△COQ,再运用全等三角形的性质即可证明;
(2)如图(2):过D作DE⊥AB,垂足为E,再根据直角三角形的性质求得AE=4,进而求得DE=,然后再说明OP为△DBE的中位线,最后根据中位线的性质即可解答;
(3)如图(3):过C作CF⊥AB交AB延长线于F,先说明四边形APCQ为平行四边形,当四边形APCQ为菱形时有AP=PC,然后在Rt△PCF中运用勾股定理解答即可.
【详解】(1)证明:∵平行四边形ABCD
∴CD//AB,OA=OC,OB=OD
∴∠DCA=∠BAC,∠CQP=∠APQ
∴△AOP≌△COQ(AAS)
∴OP=OQ;
(2)如图(2):过D作DE⊥AB,垂足为E
∵∠DAB=60°
∴AE=AD=4
∴DE=
∴BE=AB-AE=14-4=10,PE=AP-AE=9-4 =5,PB=AB-AP=5
∴PE=PB
∵OB=OD
∴OP为△DBE的中位线
∴OP=DE=;
(3)有可能,理由如下:
如图(3):过C作CF⊥AB交AB延长线于F
∵平行四边形ABCD
∴BC//AD,BC=AD
∴∠CBF=∠DAB=60°
∴BF=BC=4
∴CF=
∵OP=OQ,OA=OC
∴四边形APCQ为平行四边形
当四边形APCQ为菱形时,则需AP=CP
∵PF=AB+BF-AP=18-AP
∴在Rt△PCF中,PC2=FC2+PF2
∴AP2=()2+(18-AP)2,解得AP=.
【点睛】本题主要考查了平行四边形的性质、菱形的判定、全等三角形的判定与性质以及勾股定理等知识点,灵活应用相关性质、判定定理成为解答本题的关键.
26.(1)EB=FD
(2)EB=FD,证明见解析;
(3)∠EGD不发生变化,仍然是60°.
【分析】(1)根据等边三角形的性质可证,△AFD≌△ABE,则=;
(2)由(1)同理可证△AFD≌△ABE,从而得出EB=FD;
(3)由(2)同理得:△FAD≌△BAE,则∠AEB=∠ADF,再利用三角形内角和定理可得答案.
【详解】(1)解:EB=FD,理由如下:
∵△ADE、△ABF是等边三角形,
∴AE=AD,AB=AF,∠DAE=∠BAF,
∴∠BAE=∠DAF,
∴△AFD≌△ABE(SAS),
∴EB=FD,
(2)EB=FD,理由如下:
∵△AFB为等边三角形,
∴AF=AB,∠FAB=60,
∵△ADE为等边三角形,
∴AD=AE,∠EAD=60,
∴∠FAB+∠BAD=∠EAD+∠BAD,
即∠FAD=∠BAE,
∴△FAD≌△BAE(SAS),
∴EB=FD;
(3)不变,理由如下:
由(2)同理得:△FAD≌△BAE,
∴∠AEB=∠ADF,
设∠AEB为x,则∠ADF也为x,
于是有∠BED为(60-x),∠EDF为(60+x),
∴∠EGD=180-∠BED-∠EDF=180-(60-x)-(60+x)=60.
【点睛】本题是四边形综合题,主要考查了正方形的性质,等边三角形的性质,全等三角形的判定与性质等知识,证明△FAD≌△BAE是解题的关键.
27.(1)t,(12﹣t),(15﹣2t),2t;(2)当t=5为何值时,四边形APQB是平行四边形;(3)当t=4时,四边形PDCQ是平行四边形
【分析】(1)根据速度、路程以及时间的关系和线段之间的数量关系,即可求出AP,DP,BQ,CQ的长;
(2)当AP=BQ时,四边形APQB是平行四边形,建立关于t的一元一次方程方程,解方程求出符合题意的t值即可;
(3)当PD=CQ时,四边形PDCQ是平行四边形;建立关于t的一元一次方程方程,解方程求出符合题意的t值即可.
【详解】解:(1)t,(12﹣t),(15﹣2t),2t;
(2)根据题意有AP=t,CQ=2t,PD=12﹣t,BQ=15﹣2t.
∵AD∥BC,
∴当AP=BQ时,四边形APQB是平行四边形.
∴t=15﹣2t,
解得t=5.
∴t=5时四边形APQB是平行四边形;
(3)由AP=tcm,CQ=2tcm,
∵AD=12cm,BC=15cm,
∴PD=AD﹣AP=12﹣t,
如图1,∵AD∥BC,
∴当PD=QC时,四边形PDCQ是平行四边形.
即:12﹣t=2t,
解得t=4,
∴当t=4时,四边形PDCQ是平行四边形.
【点睛】本题考查了平行四边形的判定和性质的应用,题目是一道综合性比较强的题目,难度适中,解题的关键是把握“化动为静”的解题思想.
