第二十章:数据的分析练习题(含解析)2021-2022学年新疆地区八年级下学期人教版数学期末试题选编
文档属性
| 名称 | 第二十章:数据的分析练习题(含解析)2021-2022学年新疆地区八年级下学期人教版数学期末试题选编 |  | |
| 格式 | zip | ||
| 文件大小 | 791.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-29 21:07:52 | ||
图片预览


文档简介
第二十章:数据的分析
一、单选题
1.(2022春·新疆乌鲁木齐·八年级统考期末)某小区开展节约每一滴水活动,为了了解开展活动一个月以来节约用水的情况,从400户中随机选取20户统计了各自家庭一个月节约用水情况.表格如下:
节水量/立方米 2 2.5 3 4 0
家庭数/户 2 4 6 7 1
请你估计这400户的家庭一个月节约用水的总量大约是( )
A.2600立方米 B.1350立方米 C.1300立方米 D.1200立方米
2.(2022春·新疆阿克苏·八年级统考期末)在安全教育知识竞赛中,某校对学生成绩进行了抽样调查,被抽取的7名学生的成绩如下(单位:分):85,92,93,87,95,94,92,则这组数据的中位数和众数分别是( )
A.92,92 B.92,93 C.93,92 D.87,92
3.(2022春·新疆昌吉·八年级统考期末)冠豸中学在预防“新冠肺炎”期间,要求学生每日测量体温,八(10)班一名同学连续一周体温情况如下表所示:则该名同学这一周体温数据的众数和中位数分别是( )
36.2 36.2 36.5 36.3 36.2 36.4 36.3
A.36.3和36.2 B.36.2和36.3 C.36.2和36.2 D.36.2和36.1
4.(2022春·新疆喀什·八年级统考期末)我地区某中学组织的全校师生迎“五四”诗词大赛决赛中,25名参赛同学的得分情况如图所示.这些同学成绩的众数是( )
A.94分 B.96分 C.98分 D.100分
5.(2022春·新疆塔城·八年级统考期末)已知数据:2,1,4,6,9,8,6,1.则这组数据的中位数是( )
A.4 B.5 C.6 D.4和6
6.(2022春·新疆乌鲁木齐·八年级统考期末)甲、乙、丙、丁四名射击运动员进行射击测试,每人10次射击成绩的平均数(单位:环)及方差(单位:环)如下表所示:
甲 乙 丙 丁
9 8 9 9
1.6 0.8 3 0.8
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择( )
A.甲 B.乙 C.丙 D.丁
7.(2022春·新疆乌鲁木齐·八年级统考期末)计划从甲、乙、丙、丁四人中选出一人参加射击比赛,经过三轮的初赛,他们的平均成绩都是9环,方差分别是,,,,从成绩稳定上看,你认为谁会去最合适( )
A.甲 B.乙 C.丙 D.丁
8.(2022春·新疆乌鲁木齐·八年级统考期末)已知甲、乙两组数据的平均数都是15,甲组数据的方差s2=1,乙组数据的方差s2=8,下列结论中正确的是( )
A.甲组数据比乙组数据的波动大 B.乙组数据比甲组数据的波动大
C.甲组数据与乙组数据的波动一样大 D.甲组数据与乙组数据的波动不能比较
9.(2022春·新疆巴音郭楞·八年级统考期末)在某样本方差的计算公式s2=[(x1﹣8)2+(x2﹣8)2+…+(x10﹣8)2]中,数字10和8依次表示样本的( )
A.容量,方差 B.平均数,容量 C.容量,平均数 D.方差、平均数
二、填空题
10.(2022春·新疆喀什·八年级统考期末)九年级一班学生中,13岁的有5人,14岁的有30人,15岁的有5人,他们平均年龄是_______岁.
11.(2022春·新疆乌鲁木齐·八年级统考期末)某校规定学生的体育成绩由三部分组成:平时表现占15%,理论考试占30%,体育技能占55%,小明的上述三项成绩依次为86分、80分、88分,则小明学年总评成绩为_____.
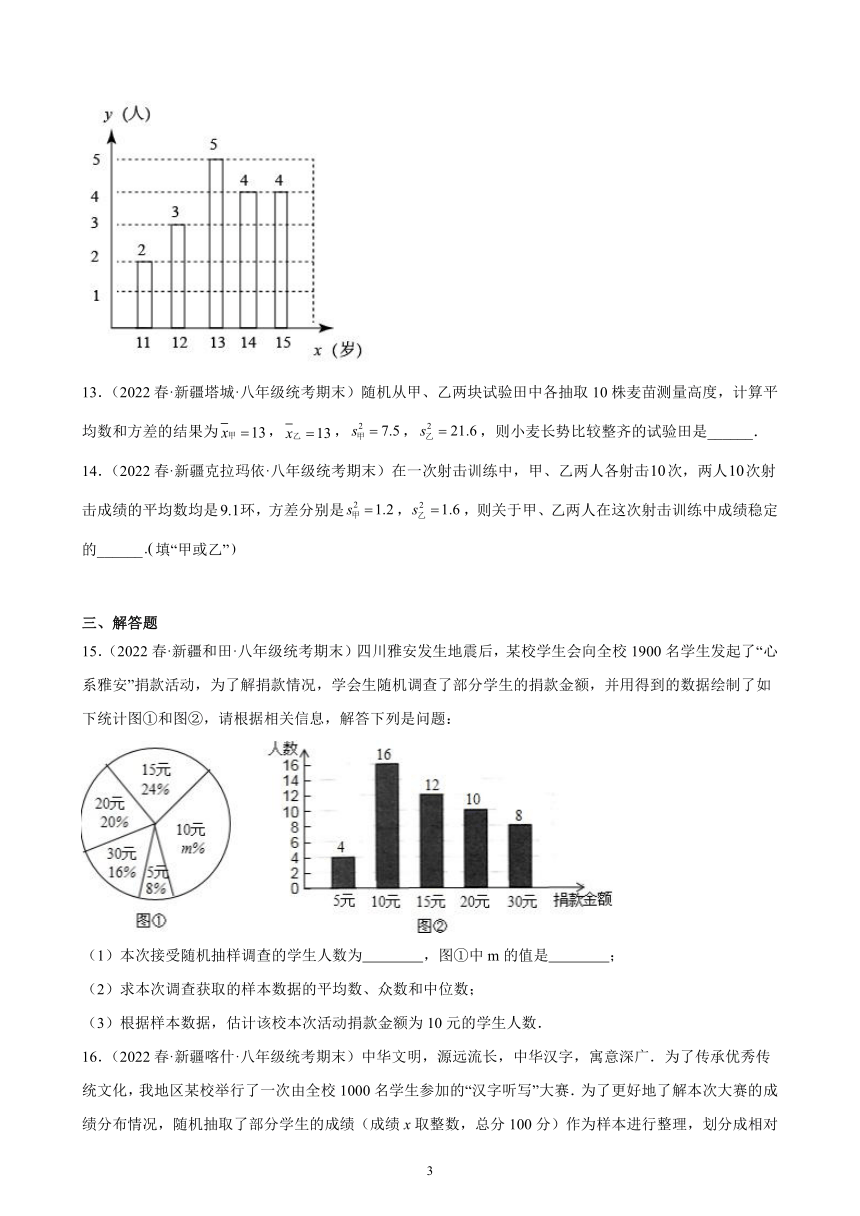
12.(2022春·新疆乌鲁木齐·八年级统考期末)如图所示是某校初中数学兴趣小组年龄结构条形统计图,该小组年龄最小为11岁,最大为15岁,根据统计图所提供的数据,该小组组员年龄的中位数为________岁.
13.(2022春·新疆塔城·八年级统考期末)随机从甲、乙两块试验田中各抽取10株麦苗测量高度,计算平均数和方差的结果为,,,,则小麦长势比较整齐的试验田是______.
14.(2022春·新疆克拉玛依·八年级统考期末)在一次射击训练中,甲、乙两人各射击次,两人次射击成绩的平均数均是环,方差分别是,,则关于甲、乙两人在这次射击训练中成绩稳定的______填“甲或乙”
三、解答题
15.(2022春·新疆和田·八年级统考期末)四川雅安发生地震后,某校学生会向全校1900名学生发起了“心系雅安”捐款活动,为了解捐款情况,学会生随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列是问题:
(1)本次接受随机抽样调查的学生人数为 ,图①中m的值是 ;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
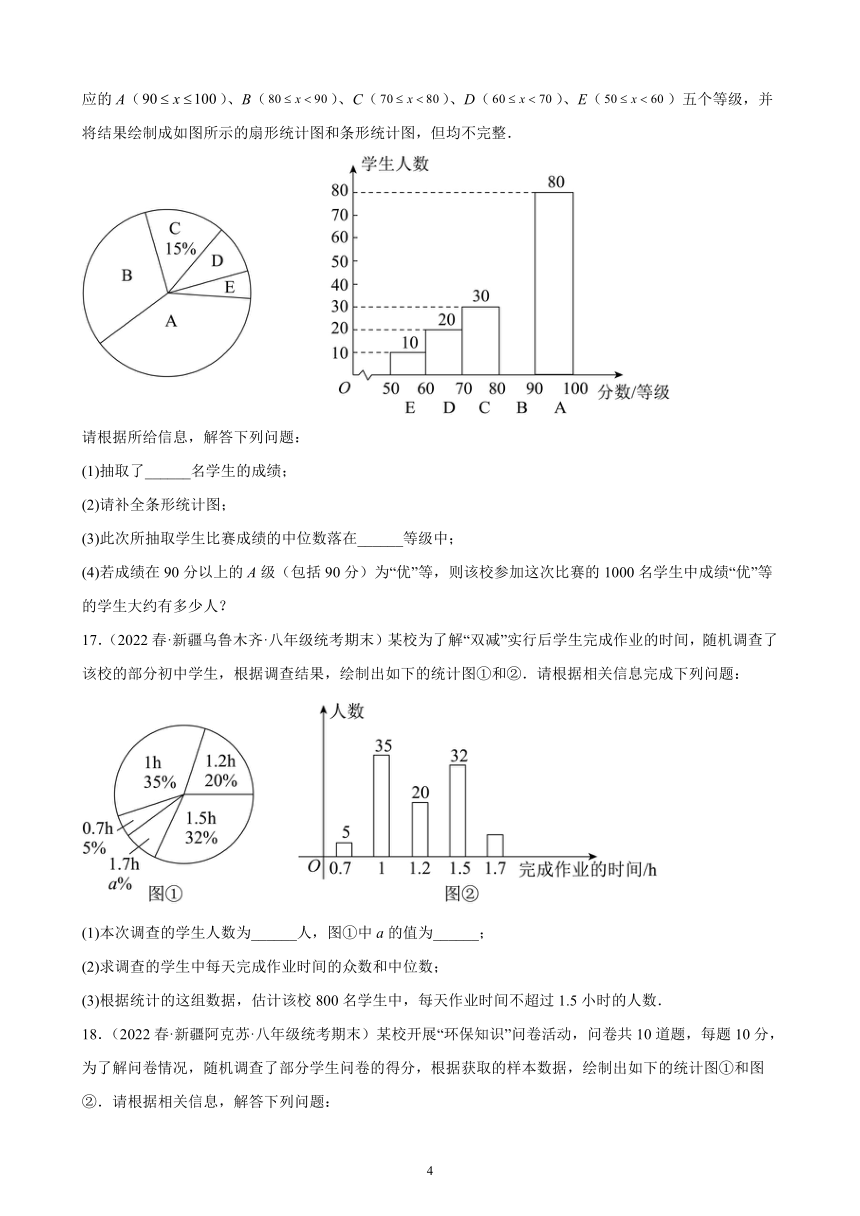
16.(2022春·新疆喀什·八年级统考期末)中华文明,源远流长,中华汉字,寓意深广.为了传承优秀传统文化,我地区某校举行了一次由全校1000名学生参加的“汉字听写”大赛.为了更好地了解本次大赛的成绩分布情况,随机抽取了部分学生的成绩(成绩x取整数,总分100分)作为样本进行整理,划分成相对应的A()、B()、C()、D()、E()五个等级,并将结果绘制成如图所示的扇形统计图和条形统计图,但均不完整.
请根据所给信息,解答下列问题:
(1)抽取了______名学生的成绩;
(2)请补全条形统计图;
(3)此次所抽取学生比赛成绩的中位数落在______等级中;
(4)若成绩在90分以上的A级(包括90分)为“优”等,则该校参加这次比赛的1000名学生中成绩“优”等的学生大约有多少人?
17.(2022春·新疆乌鲁木齐·八年级统考期末)某校为了解“双减”实行后学生完成作业的时间,随机调查了该校的部分初中学生,根据调查结果,绘制出如下的统计图①和②.请根据相关信息完成下列问题:
(1)本次调查的学生人数为______人,图①中a的值为______;
(2)求调查的学生中每天完成作业时间的众数和中位数;
(3)根据统计的这组数据,估计该校800名学生中,每天作业时间不超过1.5小时的人数.
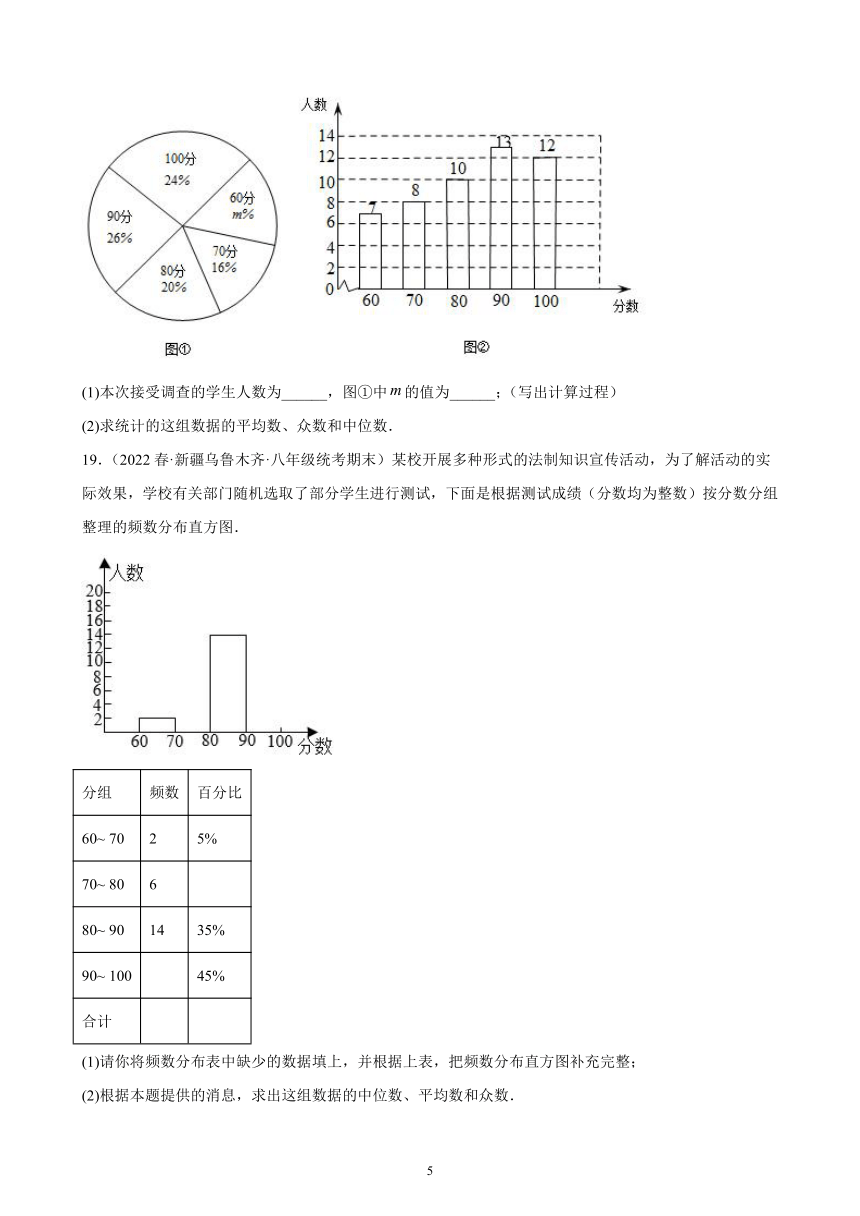
18.(2022春·新疆阿克苏·八年级统考期末)某校开展“环保知识”问卷活动,问卷共10道题,每题10分,为了解问卷情况,随机调查了部分学生问卷的得分,根据获取的样本数据,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
(1)本次接受调查的学生人数为______,图①中的值为______;(写出计算过程)
(2)求统计的这组数据的平均数、众数和中位数.
19.(2022春·新疆乌鲁木齐·八年级统考期末)某校开展多种形式的法制知识宣传活动,为了解活动的实际效果,学校有关部门随机选取了部分学生进行测试,下面是根据测试成绩(分数均为整数)按分数分组整理的频数分布直方图.
分组 频数 百分比
60~ 70 2 5%
70~ 80 6
80~ 90 14 35%
90~ 100 45%
合计
(1)请你将频数分布表中缺少的数据填上,并根据上表,把频数分布直方图补充完整;
(2)根据本题提供的消息,求出这组数据的中位数、平均数和众数.
20.(2022春·新疆巴音郭楞·八年级统考期末)某校学生会向全校名学生发起了爱心捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图1和图2,请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为 人,图中的值是 .
(2)补全图2的统计图.
(3)求本次调查获取的样本数据的平均数、众数和中位数;
(4)根据样本数据,估计该校本次活动捐款金额为元的学生人数.
21.(2022春·新疆克拉玛依·八年级统考期末)为迎接广州市青少年读书活动,某校倡议同学们利于课余时间多阅读为了解同学们的读书情况,在全校随机调查了部分同学在一周内的阅读时间,并用得到的数据绘制了统计图,根据图中信息解答下列问题:
被抽查学生阅读时间的中位数为多少小时,众数为多少小时,平均数为多少小时;
已知全校学生人数为1500人,请你估算该校学生一周内阅读时间不少于三小时的有多少人?
22.(2022春·新疆昌吉·八年级统考期末)某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分、80分、90分、100分,并根据统计数据绘制了如下不完整的统计图表:
乙校成绩统计表
分数/分 人数/人
70 7
80
90 1
100 8
(1)在图①中,“80分”所在扇形的圆心角度数为________;
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;
(4)经计算知S甲2=135,S乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
23.(2022春·新疆乌鲁木齐·八年级统考期末)某学校要调查学生关于“新冠肺炎”防治知识的了解情况,从七、八年级各随机抽取了10名学生进行测试(百分制),测试成绩整理、描述和分析如下:
(成绩得分用x表示,共分成四组:A.80≤x<85,B.85≤x<90,C.90≤x<95,D.95≤x≤100),七年级10名学生的成绩是:96,80,96,86,99,96,90,100,89,82.八年级10名学生的成绩在C组中的数据是:94,90,92.
七、八年级抽取的学生成绩统计表
年级 七年级 八年级
平均数 92 92
中位数 93 b
众数 c 100
方差 52 50.4
根据以上信息,解答下列问题:
(1)直接写出上述图表中a,b,c的值;
(2)根据以上数据,你认为该校七、八年级中哪个年级学生掌握“新冠肺炎”知识较好?请说明理由.
(3)该校七、八年级共1200人参加了此次调查活动,估计参加此次调查活动成绩优秀(x≥90)的学生人数是多少?
24.(2022春·新疆塔城·八年级统考期末)疫情期间,各地学校采取“离校不停课”,某县教科局开展“离校不停课,教师伴成长”征文活动.、两校分别推荐名教师参加了活动,其成绩(满分分)如图所示,根据图中数据解决下列问题:
校计算出了校选手的平均成绩为分,方差
请你完成:
(1)补全条形统计图;
(2)校选手成绩的众数是______分,平均成绩______分;
(3)根据(2)中计算结果,分析哪个学校的成绩较好.
参考答案:
1.D
【分析】计算20户的平均数,再乘以总户数400即可.
【详解】解:(立方米),
∴这400户的家庭一个月节约用水的总量大约是1200立方米,
故选:D.
【点睛】此题考查了平均数的计算,正确掌握平均数的计算公式是解题的关键.
2.A
【分析】首先把所给数据按从小到大排序,然后利用中位数和众数定义即可确定结果.
【详解】解:把已知数据按从小到大排序后为85,87,92,92,93, 94, 95,
处于中间位置的数是92,出现次数最多的是92,
∴中位数为92,众数为92,
故选择:A.
【点睛】本题考查了中位数和众数,熟练掌握相关定义以及求解方法是解题的关键.①给定n个数据,按从小到大排序,如果n为奇数,位于中间的那个数就是中位数;如果n为偶数,位于中间两个数的平均数就是中位数.任何一组数据,都一定存在中位数的,但中位数不一定是这组数据里的数.②给定一组数据,出现次数最多的那个数,称为这组数据的众数.
3.B
【分析】根据众数和中位数的定义求解即可.
【详解】将这组数据重新排列为:36.2、36.2、36.2、36.3、36.3、36.4、36.5,
这组数据中出现次数最多的是36.2,众数为36.2,
出现在最中间的数为36.3,中位数为36.3,
故选:B.
【点睛】本题考查众数和中位数的定义,一组数据中出现次数最多的数据叫众数;将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是中位数,如果数据的个数是偶数,则中间两个数据的平均数就是中位数,熟知定义是解题的关键.
4.C
【分析】利用众数的定义求解.
【详解】解:观察图形可知:98出现了9次,出现次数最多,所以数据的众数为98分.
故选:C.
【点睛】本题考查了众数:一组数据中出现次数最多的数据叫做众数.
5.B
【详解】解:将这组数据排序:1,1,2,4,6,6,8,9;
所以中位数是(4+6)÷2=5,
故选B.
6.D
【分析】结合表中数据,先找出平均数最大的运动员;再根据方差的意义,找出方差最小的运动员即可.
【详解】解:选择一名成绩好的运动员,从平均数最大的运动员中选取,
由表可知,甲,丙,丁的平均值最大,都是9,
∴从甲,丙,丁中选取,
∵甲的方差是1.6,丙的方差是3,丁的方差是0.8,
∴S 2丁<S 2甲<S 2乙,
∴发挥最稳定的运动员是丁,
∴从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择丁.
故选:D.
【点睛】本题重点考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
7.A
【分析】根据方差越小,成绩越稳定即可判断.
【详解】∵0.23<0.3<0.35<0.4,
∴,
∴甲成绩最稳定,
∴选甲去参赛更合适.
故选A.
【点睛】本题考查了方差,解题的关键是理解方差越小成绩越稳定.
8.B
【分析】根据方差的意义,方差越小,波动越小,越稳定进行判断即可得.
【详解】由题意得,甲组数据的方差<乙组数据的方差,
A、甲组数据没有乙组数据的波动大,故本选项错误;
B、乙组数据的比甲组数据的波动大,说法正确,故本选项正确;
C、甲组数据没有乙组数据的波动大,故本选项错误;
D、甲组数据没有乙组数据的波动大,故本选项错误,
故选B.
【点睛】本题考查了方差的意义,方差是反映一组数据的波动大小的一个量.方差越大,则它与其平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
9.C
【详解】试题分析:方差计算公式:S2=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2],n表示样本容量,为平均数,根据此公式即可得到答案.
解:由于s2=[(x1﹣8)2+(x2﹣8)2+…+(x10﹣8)2],所以样本容量是10,平均数是8.
故选C.
10.14
【分析】这里13岁的有5人,14岁的有30人,15岁的有5人,用他们的年龄和除以总人数即得.
【详解】解:∵5+30+5=40(人),
∴这班学生的平均年龄=(岁).
故答案为:14.
【点睛】本题考查了计算加权平均数,解题的关键是熟练掌握加权平均数的意义和计算方法.
11.85.3
【分析】根据加权平均数的计算公式进行计算.
【详解】解:小明学年总评成绩为:
.
故答案为:85.3.
【点睛】本题主要考查了求一组数据的加权平均数,熟练掌握加权平均数的计算公式,是解题的关键.
12.13
【分析】直接根据中位数定义求解即可.
【详解】解:根据题意排列得:11,11,12,12,12,13,13,
13,13,13,14,14,14,14,15,15,15,15,
个数为偶数,中间的两个数为:13,13,
∴中位数为13,
故答案为:13
【点睛】本题主要考查中位数的定义,将一组数据按照从小到大(或从大到小)的顺序排列,如果这组数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
13.甲
【分析】根据方差的意义判断即可,方差反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
【详解】解:∵,,,,
∴,,
∵甲块试验田的方差小,
∴甲试验田小麦长势比较整齐.
故答案为:甲.
【点睛】本题主要考查了方差的意义,解题的关键是熟练掌握方差的意义:它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
14.甲
【分析】根据方差的意义解答即可.
【详解】∵,,
∴,
则甲、乙两人在这次射击训练中成绩稳定的是甲.
故答案为:甲.
【点睛】本题考查了方差的意义,方差越小,越稳定.
15.(1)50; 32;(2)16;10;15;(3)608人.
【分析】(1)根据条形统计图即可得出样本容量:4+16+12+10+8=50(人);根据扇形统计图得出m的值:;
(2)利用平均数、中位数、众数的定义分别求出即可.
(3)根据样本中捐款10元的百分比,从而得出该校本次活动捐款金额为10元的学生人数.
【详解】解:(1)根据条形图4+16+12+10+8=50(人),
m=100-20-24-16-8=32;
故答案为:50; 32.
(2)∵,
∴这组数据的平均数为:16.
∵在这组样本数据中,10出现次数最多为16次,
∴这组数据的众数为:10.
∵将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是15,
∴这组数据的中位数为:,
(3)∵在50名学生中,捐款金额为10元的学生人数比例为32%,
∴由样本数据,估计该校1900名学生中捐款金额为10元的学生人数有1900×32%=608人.
∴该校本次活动捐款金额为10元的学生约有608人.
【点睛】此题主要考查了平均数、众数、中位数的统计意义以及利用样本估计总体等知识.找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数;众数是一组数据中出现次数最多的数据,注意众数可以不止一个;平均数是指在一组数据中所有数据之和再除以数据的个数.
16.(1)200
(2)见解析
(3)B
(4)400人
【分析】(1 )用C组的学生人数除以C组在扇形图中所占的百分比即可求解;
(2)根据(1) 的计算结果,用总人数减去E,D,C,A组的人数就是B组的人数,即可补全频数分布直方图;
(3)根据中位数的定义,将这组数据按照从小到大的顺序排列后,处于中间位置的数据(或中间两数据的平均数)即为中位数;
(4)利用总数1000乘以90分以上的A级的学生的所占的频率即可求出;
(1)
30÷15%=200(人)
所以抽取了200名学生的成绩,
故答案为:200;
(2)200-10-20-30-80=60(人)
补全频数分布直方图,如下:
(3)
一共有200个数据,按照从小到大的顺序排列后,第100个与第101个数据都落在第四个分数段,所以这次比赛成绩的中位数会落在80≤x<90分数段(B组).
故答案为:B;
(4)
1000× =400(人);
所以该校参加这次比赛的1000名学生中成绩“优”等的学生大约有400人.
【点睛】本题考查读扇形图和频数(率)分布直方图的能力,以及利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题,也考查了中位数和利用样本估计总体.
17.(1)100,8
(2)众数:1h,中位数:1.2h
(3)736人
【分析】(1)样本中“1h”的人数是35,占调查人数的35%,可求出调查人数,进而求出“1.7h”所占的百分比,确定a的值;
(2)根据中位数、众数的意义和计算方法,分别求出结果即可;
(3)用样本中不超过1.5小时的百分数来估计总体中的百分数,即可求出答案.
(1)
35÷35%=100(人),100%-(5%+35%+20%+32%)=8%,
故答案为:100,8;
(2)
这组完成作业时间出现次数最多的是1,因此众数是1h,
将这100个数据从小到大排列后,处在中间位置的两个数都是1.2,因此中位数是1.2h,
答:这组数据的众数是1h,中位数是1.2h.
(3)
(人)
答:每天作业不超过1.5小时的学生约有736人.
【点睛】本题考查条形统计图、扇形统计图的意义和制作方法,理解统计图中的数量关系是正确解题的关键.
18.(1)50;14;
(2)这组数据的平均数是83,中位数是85,众数是90.
【分析】(1)根据每个组的频数可以求得本次接受调查的学生人数,即可得m的值;
(2)根据条形统计图中的数据,可以得到这40个样本数据平均数、众数、中位数.
(1)
7+8+10+13+12=50(人),7÷50=14%,
故答案为:50;14;
(2)
观察条形统计图,
∵,
∴这组数据的平均数是83,
∵在这组数据中,90出现了13次,出现的次数最多,
∴这组数据的众数为90,
∵将这组数据按从小到大的顺序排列,其中处于中间的两个数是80,90,有=85,
∴这组数据的平均数是83,中位数是85,众数是90.
【点睛】本题考查条形统计图、扇形统计图,解答本题的关键是明确题意,利用数形结合的思想解答.
19.(1)图见解析;
(2)中位数:85;平均数:87;众数:95
【分析】(1)先求出补选取的总人数,再计算出频数分布表中缺少的数据,然后再把频数分布直方图补充完整即可;
(2)根据中位数、平均数和众数的定义求解即可.
(1)
被选取的人数为:(人),
70~ 80分所占百分比为:,
90~ 100分的人数有:(人)
填表为:
分组 频数 百分比
60~ 70 2 5%
70~ 80 6 15%
80~ 90 14 35%
90~ 100 18 45%
合计 40 1.00
补全条形统计图如下:
(2)
由组中值可得,60~70分的组中值为65分,70~80分的组中值为75分,80~90分的组中值为85分,90~100分的组中值为95分;
40个数据的中位数落在80~90分这一组,故中位位数为85分;
平均数为:(分);
落在90~100分的数据最多,故众数为:95分.
【点睛】本题主要考查了频数分布表和频数分布直方图,以及由组中值确定众数、中位数和平均数,计算组中值是解答本题的关键.
20.(1)、;(2)详见解析;(3)平均数:16;众数:10;中位数:15;(4)608.
【分析】(1)由元的人数及其所占百分比可得总人数,用元人数除以总人数可得m的值;
(2)总人数乘以元对应百分比可得其人数,据此可补全图形;
(3)根据统计图可以分别得到本次调查获取的样本数据的平均数、众数和中位数;
(4)根据统计图中的数据可以估计该校本次活动捐款金额为元的学生人数.
【详解】(1)本次接受随机抽样调查的学生人数为人.
∵
∴ .
故答案为、;
(2)元的人数为,补全图形如下:
(3)本次调查获取的样本数据的平均数是: (元),
本次调查获取的样本数据的最多的是10,众数是:元,
本次调查获取的样本数据的中位数是:元;
(4)估计该校本次活动捐款金额为元的学生人数为人.
【点睛】本题考查了条形统计图、扇形统计图、用样本估计总体、中位数、众数,解题的关键是明确题意,找出所求问题需要的条件.
21.2,2,;估算该校学生一周内阅读时间不少于三小时的有540人.
【分析】(1)根据统计图中的数据确定出学生劳动时间的众数、中位数和平均数即可;
(2)根据总人数 阅读时间不少于三小时的百分比可得结果.
【详解】,
被抽查学生阅读时间的中位数为:第25和第26个学生阅读时间的平均数,
众数为2,
平均数,
,
答:估算该校学生一周内阅读时间不少于三小时的有540人.
故答案为(1) 2, 2, 2.34;(2)估算该校学生一周内阅读时间不少于三小时的有540人.
【点睛】本题考查众数,条形统计图,平均数、中位数及用样本估计总体,解题的关键是弄清题中的数据.
22.(1)54°;(2)补图见解析;(3)85分;(4)甲校20名同学的成绩相对乙校较整齐.
【分析】(1)根据统计图可知甲班70分的有6人,从而可求得总人数,然后可求得成绩为80分的同学所占的百分比,最后根据圆心角的度数=360°×百分比即可求得答案;
(2)用总人数减去成绩为70分、80分、90分的人数即可求得成绩为100分的人数,从而可补全统计图;
(3)先求得乙班成绩为80分的人数,然后利用加权平均数公式计算平均数;
(4)根据方差的意义即可做出评价.
【详解】解:(1)6÷30%=20,
3÷20=15%,
360°×15%=54°;
(2)20-6-3-6=5,统计图补充如下:
(3)20-1-7-8=4,
=85;
(4)∵S甲2<S乙2,
∴甲班20同名同学的成绩比较整齐.
23.(1)a=40,b=93,c=96;(2)八年级掌握得更好,见解析;(3)780名
【分析】(1)先根据扇形统计图求解组的学生人数,结合组人数,求解组人数,可得的值,再根据八年级学生成绩的中位数落在组,可得的值,由七年级学生成绩中分有个,出现的次数最多,可得的值;
(2)因为两个年级的平均数与中位数相同,所以从众数与方差两个分面分析可得结论;
(3)分别统计出七年级、八年级成绩大于或等于分的人数,利用样本的百分率估计总体即可得到答案.
【详解】解:(1)因为八年级组有人,组有人,组有人,
所以组有人,所以: 即
因为八年级学生成绩的分布:组有人,组有人,组有人,组有人,且成绩是按照从小到大的顺序排列的,所以八年级学生成绩的中位数落在组,而C组中的数据是:94,90,92,
按从小到大排列为:
所以第个,第个数据为:
所以中位数为:分,
因为七年级学生成绩中分有个,出现的次数最多,所以众数分,
故答案为:a=40,b=93,c=96.
(2)八年级掌握得更好.因为七八年级的平均数、中位数相同,
而八年级的众数比七年级高,说明八年级高分的同学更多;
八年级方差比七年级小,说明八年级两极分化差距小.
(3)由题意得:七年级成绩大于或等于分的有人,八年级成绩大于或等于分的有人
(人)
答:参加此次调查活动成绩优秀的学生人数约为780人.
【点睛】本题考查的是扇形统计图,频数分布,平均数,众数,中位数,方差的含义及应用,同时考查了利用样本估计总体,掌握以上知识是解题的关键.
24.(1)详见解析;(2),;(3)详见解析
【分析】(1)根据A校选手的平均成绩可以算出总成绩,减去已知的4名选手成绩即可得到2号选手成绩,据此可以补全条形统计图;
(2)阅读条形统计图,再根据众数和平均数的意义,可以算得答案;
(3)可以分别从成绩稳定性和高分人数多少两个方面作出比较.
【详解】(1)∵
∴可以补全条形统计图如下:
(2)阅读条形统计图,发现B校5名选手成绩中,100分有两个,其他70、75、80各一个,所以B校选手成绩的众数是100分,B校选手的平均成绩=(70+75+80+100+100)÷5=85分.
故答案是;.
(3)解:∵
∴从稳定性方面考虑,两校平均成绩相等,但是A校方差较小,所以A校成绩比较稳定;
从高分人数方面考虑,B校众数为100分,A校众数为85分,100>80,所以B校高分众数多.
【点睛】本题考查数据分析指标的计算,根据公式正确计算各项指标,并作出合理分析是解题关键.
一、单选题
1.(2022春·新疆乌鲁木齐·八年级统考期末)某小区开展节约每一滴水活动,为了了解开展活动一个月以来节约用水的情况,从400户中随机选取20户统计了各自家庭一个月节约用水情况.表格如下:
节水量/立方米 2 2.5 3 4 0
家庭数/户 2 4 6 7 1
请你估计这400户的家庭一个月节约用水的总量大约是( )
A.2600立方米 B.1350立方米 C.1300立方米 D.1200立方米
2.(2022春·新疆阿克苏·八年级统考期末)在安全教育知识竞赛中,某校对学生成绩进行了抽样调查,被抽取的7名学生的成绩如下(单位:分):85,92,93,87,95,94,92,则这组数据的中位数和众数分别是( )
A.92,92 B.92,93 C.93,92 D.87,92
3.(2022春·新疆昌吉·八年级统考期末)冠豸中学在预防“新冠肺炎”期间,要求学生每日测量体温,八(10)班一名同学连续一周体温情况如下表所示:则该名同学这一周体温数据的众数和中位数分别是( )
36.2 36.2 36.5 36.3 36.2 36.4 36.3
A.36.3和36.2 B.36.2和36.3 C.36.2和36.2 D.36.2和36.1
4.(2022春·新疆喀什·八年级统考期末)我地区某中学组织的全校师生迎“五四”诗词大赛决赛中,25名参赛同学的得分情况如图所示.这些同学成绩的众数是( )
A.94分 B.96分 C.98分 D.100分
5.(2022春·新疆塔城·八年级统考期末)已知数据:2,1,4,6,9,8,6,1.则这组数据的中位数是( )
A.4 B.5 C.6 D.4和6
6.(2022春·新疆乌鲁木齐·八年级统考期末)甲、乙、丙、丁四名射击运动员进行射击测试,每人10次射击成绩的平均数(单位:环)及方差(单位:环)如下表所示:
甲 乙 丙 丁
9 8 9 9
1.6 0.8 3 0.8
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择( )
A.甲 B.乙 C.丙 D.丁
7.(2022春·新疆乌鲁木齐·八年级统考期末)计划从甲、乙、丙、丁四人中选出一人参加射击比赛,经过三轮的初赛,他们的平均成绩都是9环,方差分别是,,,,从成绩稳定上看,你认为谁会去最合适( )
A.甲 B.乙 C.丙 D.丁
8.(2022春·新疆乌鲁木齐·八年级统考期末)已知甲、乙两组数据的平均数都是15,甲组数据的方差s2=1,乙组数据的方差s2=8,下列结论中正确的是( )
A.甲组数据比乙组数据的波动大 B.乙组数据比甲组数据的波动大
C.甲组数据与乙组数据的波动一样大 D.甲组数据与乙组数据的波动不能比较
9.(2022春·新疆巴音郭楞·八年级统考期末)在某样本方差的计算公式s2=[(x1﹣8)2+(x2﹣8)2+…+(x10﹣8)2]中,数字10和8依次表示样本的( )
A.容量,方差 B.平均数,容量 C.容量,平均数 D.方差、平均数
二、填空题
10.(2022春·新疆喀什·八年级统考期末)九年级一班学生中,13岁的有5人,14岁的有30人,15岁的有5人,他们平均年龄是_______岁.
11.(2022春·新疆乌鲁木齐·八年级统考期末)某校规定学生的体育成绩由三部分组成:平时表现占15%,理论考试占30%,体育技能占55%,小明的上述三项成绩依次为86分、80分、88分,则小明学年总评成绩为_____.
12.(2022春·新疆乌鲁木齐·八年级统考期末)如图所示是某校初中数学兴趣小组年龄结构条形统计图,该小组年龄最小为11岁,最大为15岁,根据统计图所提供的数据,该小组组员年龄的中位数为________岁.
13.(2022春·新疆塔城·八年级统考期末)随机从甲、乙两块试验田中各抽取10株麦苗测量高度,计算平均数和方差的结果为,,,,则小麦长势比较整齐的试验田是______.
14.(2022春·新疆克拉玛依·八年级统考期末)在一次射击训练中,甲、乙两人各射击次,两人次射击成绩的平均数均是环,方差分别是,,则关于甲、乙两人在这次射击训练中成绩稳定的______填“甲或乙”
三、解答题
15.(2022春·新疆和田·八年级统考期末)四川雅安发生地震后,某校学生会向全校1900名学生发起了“心系雅安”捐款活动,为了解捐款情况,学会生随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列是问题:
(1)本次接受随机抽样调查的学生人数为 ,图①中m的值是 ;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
16.(2022春·新疆喀什·八年级统考期末)中华文明,源远流长,中华汉字,寓意深广.为了传承优秀传统文化,我地区某校举行了一次由全校1000名学生参加的“汉字听写”大赛.为了更好地了解本次大赛的成绩分布情况,随机抽取了部分学生的成绩(成绩x取整数,总分100分)作为样本进行整理,划分成相对应的A()、B()、C()、D()、E()五个等级,并将结果绘制成如图所示的扇形统计图和条形统计图,但均不完整.
请根据所给信息,解答下列问题:
(1)抽取了______名学生的成绩;
(2)请补全条形统计图;
(3)此次所抽取学生比赛成绩的中位数落在______等级中;
(4)若成绩在90分以上的A级(包括90分)为“优”等,则该校参加这次比赛的1000名学生中成绩“优”等的学生大约有多少人?
17.(2022春·新疆乌鲁木齐·八年级统考期末)某校为了解“双减”实行后学生完成作业的时间,随机调查了该校的部分初中学生,根据调查结果,绘制出如下的统计图①和②.请根据相关信息完成下列问题:
(1)本次调查的学生人数为______人,图①中a的值为______;
(2)求调查的学生中每天完成作业时间的众数和中位数;
(3)根据统计的这组数据,估计该校800名学生中,每天作业时间不超过1.5小时的人数.
18.(2022春·新疆阿克苏·八年级统考期末)某校开展“环保知识”问卷活动,问卷共10道题,每题10分,为了解问卷情况,随机调查了部分学生问卷的得分,根据获取的样本数据,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
(1)本次接受调查的学生人数为______,图①中的值为______;(写出计算过程)
(2)求统计的这组数据的平均数、众数和中位数.
19.(2022春·新疆乌鲁木齐·八年级统考期末)某校开展多种形式的法制知识宣传活动,为了解活动的实际效果,学校有关部门随机选取了部分学生进行测试,下面是根据测试成绩(分数均为整数)按分数分组整理的频数分布直方图.
分组 频数 百分比
60~ 70 2 5%
70~ 80 6
80~ 90 14 35%
90~ 100 45%
合计
(1)请你将频数分布表中缺少的数据填上,并根据上表,把频数分布直方图补充完整;
(2)根据本题提供的消息,求出这组数据的中位数、平均数和众数.
20.(2022春·新疆巴音郭楞·八年级统考期末)某校学生会向全校名学生发起了爱心捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图1和图2,请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为 人,图中的值是 .
(2)补全图2的统计图.
(3)求本次调查获取的样本数据的平均数、众数和中位数;
(4)根据样本数据,估计该校本次活动捐款金额为元的学生人数.
21.(2022春·新疆克拉玛依·八年级统考期末)为迎接广州市青少年读书活动,某校倡议同学们利于课余时间多阅读为了解同学们的读书情况,在全校随机调查了部分同学在一周内的阅读时间,并用得到的数据绘制了统计图,根据图中信息解答下列问题:
被抽查学生阅读时间的中位数为多少小时,众数为多少小时,平均数为多少小时;
已知全校学生人数为1500人,请你估算该校学生一周内阅读时间不少于三小时的有多少人?
22.(2022春·新疆昌吉·八年级统考期末)某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分、80分、90分、100分,并根据统计数据绘制了如下不完整的统计图表:
乙校成绩统计表
分数/分 人数/人
70 7
80
90 1
100 8
(1)在图①中,“80分”所在扇形的圆心角度数为________;
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;
(4)经计算知S甲2=135,S乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
23.(2022春·新疆乌鲁木齐·八年级统考期末)某学校要调查学生关于“新冠肺炎”防治知识的了解情况,从七、八年级各随机抽取了10名学生进行测试(百分制),测试成绩整理、描述和分析如下:
(成绩得分用x表示,共分成四组:A.80≤x<85,B.85≤x<90,C.90≤x<95,D.95≤x≤100),七年级10名学生的成绩是:96,80,96,86,99,96,90,100,89,82.八年级10名学生的成绩在C组中的数据是:94,90,92.
七、八年级抽取的学生成绩统计表
年级 七年级 八年级
平均数 92 92
中位数 93 b
众数 c 100
方差 52 50.4
根据以上信息,解答下列问题:
(1)直接写出上述图表中a,b,c的值;
(2)根据以上数据,你认为该校七、八年级中哪个年级学生掌握“新冠肺炎”知识较好?请说明理由.
(3)该校七、八年级共1200人参加了此次调查活动,估计参加此次调查活动成绩优秀(x≥90)的学生人数是多少?
24.(2022春·新疆塔城·八年级统考期末)疫情期间,各地学校采取“离校不停课”,某县教科局开展“离校不停课,教师伴成长”征文活动.、两校分别推荐名教师参加了活动,其成绩(满分分)如图所示,根据图中数据解决下列问题:
校计算出了校选手的平均成绩为分,方差
请你完成:
(1)补全条形统计图;
(2)校选手成绩的众数是______分,平均成绩______分;
(3)根据(2)中计算结果,分析哪个学校的成绩较好.
参考答案:
1.D
【分析】计算20户的平均数,再乘以总户数400即可.
【详解】解:(立方米),
∴这400户的家庭一个月节约用水的总量大约是1200立方米,
故选:D.
【点睛】此题考查了平均数的计算,正确掌握平均数的计算公式是解题的关键.
2.A
【分析】首先把所给数据按从小到大排序,然后利用中位数和众数定义即可确定结果.
【详解】解:把已知数据按从小到大排序后为85,87,92,92,93, 94, 95,
处于中间位置的数是92,出现次数最多的是92,
∴中位数为92,众数为92,
故选择:A.
【点睛】本题考查了中位数和众数,熟练掌握相关定义以及求解方法是解题的关键.①给定n个数据,按从小到大排序,如果n为奇数,位于中间的那个数就是中位数;如果n为偶数,位于中间两个数的平均数就是中位数.任何一组数据,都一定存在中位数的,但中位数不一定是这组数据里的数.②给定一组数据,出现次数最多的那个数,称为这组数据的众数.
3.B
【分析】根据众数和中位数的定义求解即可.
【详解】将这组数据重新排列为:36.2、36.2、36.2、36.3、36.3、36.4、36.5,
这组数据中出现次数最多的是36.2,众数为36.2,
出现在最中间的数为36.3,中位数为36.3,
故选:B.
【点睛】本题考查众数和中位数的定义,一组数据中出现次数最多的数据叫众数;将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是中位数,如果数据的个数是偶数,则中间两个数据的平均数就是中位数,熟知定义是解题的关键.
4.C
【分析】利用众数的定义求解.
【详解】解:观察图形可知:98出现了9次,出现次数最多,所以数据的众数为98分.
故选:C.
【点睛】本题考查了众数:一组数据中出现次数最多的数据叫做众数.
5.B
【详解】解:将这组数据排序:1,1,2,4,6,6,8,9;
所以中位数是(4+6)÷2=5,
故选B.
6.D
【分析】结合表中数据,先找出平均数最大的运动员;再根据方差的意义,找出方差最小的运动员即可.
【详解】解:选择一名成绩好的运动员,从平均数最大的运动员中选取,
由表可知,甲,丙,丁的平均值最大,都是9,
∴从甲,丙,丁中选取,
∵甲的方差是1.6,丙的方差是3,丁的方差是0.8,
∴S 2丁<S 2甲<S 2乙,
∴发挥最稳定的运动员是丁,
∴从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择丁.
故选:D.
【点睛】本题重点考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
7.A
【分析】根据方差越小,成绩越稳定即可判断.
【详解】∵0.23<0.3<0.35<0.4,
∴,
∴甲成绩最稳定,
∴选甲去参赛更合适.
故选A.
【点睛】本题考查了方差,解题的关键是理解方差越小成绩越稳定.
8.B
【分析】根据方差的意义,方差越小,波动越小,越稳定进行判断即可得.
【详解】由题意得,甲组数据的方差<乙组数据的方差,
A、甲组数据没有乙组数据的波动大,故本选项错误;
B、乙组数据的比甲组数据的波动大,说法正确,故本选项正确;
C、甲组数据没有乙组数据的波动大,故本选项错误;
D、甲组数据没有乙组数据的波动大,故本选项错误,
故选B.
【点睛】本题考查了方差的意义,方差是反映一组数据的波动大小的一个量.方差越大,则它与其平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
9.C
【详解】试题分析:方差计算公式:S2=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2],n表示样本容量,为平均数,根据此公式即可得到答案.
解:由于s2=[(x1﹣8)2+(x2﹣8)2+…+(x10﹣8)2],所以样本容量是10,平均数是8.
故选C.
10.14
【分析】这里13岁的有5人,14岁的有30人,15岁的有5人,用他们的年龄和除以总人数即得.
【详解】解:∵5+30+5=40(人),
∴这班学生的平均年龄=(岁).
故答案为:14.
【点睛】本题考查了计算加权平均数,解题的关键是熟练掌握加权平均数的意义和计算方法.
11.85.3
【分析】根据加权平均数的计算公式进行计算.
【详解】解:小明学年总评成绩为:
.
故答案为:85.3.
【点睛】本题主要考查了求一组数据的加权平均数,熟练掌握加权平均数的计算公式,是解题的关键.
12.13
【分析】直接根据中位数定义求解即可.
【详解】解:根据题意排列得:11,11,12,12,12,13,13,
13,13,13,14,14,14,14,15,15,15,15,
个数为偶数,中间的两个数为:13,13,
∴中位数为13,
故答案为:13
【点睛】本题主要考查中位数的定义,将一组数据按照从小到大(或从大到小)的顺序排列,如果这组数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
13.甲
【分析】根据方差的意义判断即可,方差反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
【详解】解:∵,,,,
∴,,
∵甲块试验田的方差小,
∴甲试验田小麦长势比较整齐.
故答案为:甲.
【点睛】本题主要考查了方差的意义,解题的关键是熟练掌握方差的意义:它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
14.甲
【分析】根据方差的意义解答即可.
【详解】∵,,
∴,
则甲、乙两人在这次射击训练中成绩稳定的是甲.
故答案为:甲.
【点睛】本题考查了方差的意义,方差越小,越稳定.
15.(1)50; 32;(2)16;10;15;(3)608人.
【分析】(1)根据条形统计图即可得出样本容量:4+16+12+10+8=50(人);根据扇形统计图得出m的值:;
(2)利用平均数、中位数、众数的定义分别求出即可.
(3)根据样本中捐款10元的百分比,从而得出该校本次活动捐款金额为10元的学生人数.
【详解】解:(1)根据条形图4+16+12+10+8=50(人),
m=100-20-24-16-8=32;
故答案为:50; 32.
(2)∵,
∴这组数据的平均数为:16.
∵在这组样本数据中,10出现次数最多为16次,
∴这组数据的众数为:10.
∵将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是15,
∴这组数据的中位数为:,
(3)∵在50名学生中,捐款金额为10元的学生人数比例为32%,
∴由样本数据,估计该校1900名学生中捐款金额为10元的学生人数有1900×32%=608人.
∴该校本次活动捐款金额为10元的学生约有608人.
【点睛】此题主要考查了平均数、众数、中位数的统计意义以及利用样本估计总体等知识.找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数;众数是一组数据中出现次数最多的数据,注意众数可以不止一个;平均数是指在一组数据中所有数据之和再除以数据的个数.
16.(1)200
(2)见解析
(3)B
(4)400人
【分析】(1 )用C组的学生人数除以C组在扇形图中所占的百分比即可求解;
(2)根据(1) 的计算结果,用总人数减去E,D,C,A组的人数就是B组的人数,即可补全频数分布直方图;
(3)根据中位数的定义,将这组数据按照从小到大的顺序排列后,处于中间位置的数据(或中间两数据的平均数)即为中位数;
(4)利用总数1000乘以90分以上的A级的学生的所占的频率即可求出;
(1)
30÷15%=200(人)
所以抽取了200名学生的成绩,
故答案为:200;
(2)200-10-20-30-80=60(人)
补全频数分布直方图,如下:
(3)
一共有200个数据,按照从小到大的顺序排列后,第100个与第101个数据都落在第四个分数段,所以这次比赛成绩的中位数会落在80≤x<90分数段(B组).
故答案为:B;
(4)
1000× =400(人);
所以该校参加这次比赛的1000名学生中成绩“优”等的学生大约有400人.
【点睛】本题考查读扇形图和频数(率)分布直方图的能力,以及利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题,也考查了中位数和利用样本估计总体.
17.(1)100,8
(2)众数:1h,中位数:1.2h
(3)736人
【分析】(1)样本中“1h”的人数是35,占调查人数的35%,可求出调查人数,进而求出“1.7h”所占的百分比,确定a的值;
(2)根据中位数、众数的意义和计算方法,分别求出结果即可;
(3)用样本中不超过1.5小时的百分数来估计总体中的百分数,即可求出答案.
(1)
35÷35%=100(人),100%-(5%+35%+20%+32%)=8%,
故答案为:100,8;
(2)
这组完成作业时间出现次数最多的是1,因此众数是1h,
将这100个数据从小到大排列后,处在中间位置的两个数都是1.2,因此中位数是1.2h,
答:这组数据的众数是1h,中位数是1.2h.
(3)
(人)
答:每天作业不超过1.5小时的学生约有736人.
【点睛】本题考查条形统计图、扇形统计图的意义和制作方法,理解统计图中的数量关系是正确解题的关键.
18.(1)50;14;
(2)这组数据的平均数是83,中位数是85,众数是90.
【分析】(1)根据每个组的频数可以求得本次接受调查的学生人数,即可得m的值;
(2)根据条形统计图中的数据,可以得到这40个样本数据平均数、众数、中位数.
(1)
7+8+10+13+12=50(人),7÷50=14%,
故答案为:50;14;
(2)
观察条形统计图,
∵,
∴这组数据的平均数是83,
∵在这组数据中,90出现了13次,出现的次数最多,
∴这组数据的众数为90,
∵将这组数据按从小到大的顺序排列,其中处于中间的两个数是80,90,有=85,
∴这组数据的平均数是83,中位数是85,众数是90.
【点睛】本题考查条形统计图、扇形统计图,解答本题的关键是明确题意,利用数形结合的思想解答.
19.(1)图见解析;
(2)中位数:85;平均数:87;众数:95
【分析】(1)先求出补选取的总人数,再计算出频数分布表中缺少的数据,然后再把频数分布直方图补充完整即可;
(2)根据中位数、平均数和众数的定义求解即可.
(1)
被选取的人数为:(人),
70~ 80分所占百分比为:,
90~ 100分的人数有:(人)
填表为:
分组 频数 百分比
60~ 70 2 5%
70~ 80 6 15%
80~ 90 14 35%
90~ 100 18 45%
合计 40 1.00
补全条形统计图如下:
(2)
由组中值可得,60~70分的组中值为65分,70~80分的组中值为75分,80~90分的组中值为85分,90~100分的组中值为95分;
40个数据的中位数落在80~90分这一组,故中位位数为85分;
平均数为:(分);
落在90~100分的数据最多,故众数为:95分.
【点睛】本题主要考查了频数分布表和频数分布直方图,以及由组中值确定众数、中位数和平均数,计算组中值是解答本题的关键.
20.(1)、;(2)详见解析;(3)平均数:16;众数:10;中位数:15;(4)608.
【分析】(1)由元的人数及其所占百分比可得总人数,用元人数除以总人数可得m的值;
(2)总人数乘以元对应百分比可得其人数,据此可补全图形;
(3)根据统计图可以分别得到本次调查获取的样本数据的平均数、众数和中位数;
(4)根据统计图中的数据可以估计该校本次活动捐款金额为元的学生人数.
【详解】(1)本次接受随机抽样调查的学生人数为人.
∵
∴ .
故答案为、;
(2)元的人数为,补全图形如下:
(3)本次调查获取的样本数据的平均数是: (元),
本次调查获取的样本数据的最多的是10,众数是:元,
本次调查获取的样本数据的中位数是:元;
(4)估计该校本次活动捐款金额为元的学生人数为人.
【点睛】本题考查了条形统计图、扇形统计图、用样本估计总体、中位数、众数,解题的关键是明确题意,找出所求问题需要的条件.
21.2,2,;估算该校学生一周内阅读时间不少于三小时的有540人.
【分析】(1)根据统计图中的数据确定出学生劳动时间的众数、中位数和平均数即可;
(2)根据总人数 阅读时间不少于三小时的百分比可得结果.
【详解】,
被抽查学生阅读时间的中位数为:第25和第26个学生阅读时间的平均数,
众数为2,
平均数,
,
答:估算该校学生一周内阅读时间不少于三小时的有540人.
故答案为(1) 2, 2, 2.34;(2)估算该校学生一周内阅读时间不少于三小时的有540人.
【点睛】本题考查众数,条形统计图,平均数、中位数及用样本估计总体,解题的关键是弄清题中的数据.
22.(1)54°;(2)补图见解析;(3)85分;(4)甲校20名同学的成绩相对乙校较整齐.
【分析】(1)根据统计图可知甲班70分的有6人,从而可求得总人数,然后可求得成绩为80分的同学所占的百分比,最后根据圆心角的度数=360°×百分比即可求得答案;
(2)用总人数减去成绩为70分、80分、90分的人数即可求得成绩为100分的人数,从而可补全统计图;
(3)先求得乙班成绩为80分的人数,然后利用加权平均数公式计算平均数;
(4)根据方差的意义即可做出评价.
【详解】解:(1)6÷30%=20,
3÷20=15%,
360°×15%=54°;
(2)20-6-3-6=5,统计图补充如下:
(3)20-1-7-8=4,
=85;
(4)∵S甲2<S乙2,
∴甲班20同名同学的成绩比较整齐.
23.(1)a=40,b=93,c=96;(2)八年级掌握得更好,见解析;(3)780名
【分析】(1)先根据扇形统计图求解组的学生人数,结合组人数,求解组人数,可得的值,再根据八年级学生成绩的中位数落在组,可得的值,由七年级学生成绩中分有个,出现的次数最多,可得的值;
(2)因为两个年级的平均数与中位数相同,所以从众数与方差两个分面分析可得结论;
(3)分别统计出七年级、八年级成绩大于或等于分的人数,利用样本的百分率估计总体即可得到答案.
【详解】解:(1)因为八年级组有人,组有人,组有人,
所以组有人,所以: 即
因为八年级学生成绩的分布:组有人,组有人,组有人,组有人,且成绩是按照从小到大的顺序排列的,所以八年级学生成绩的中位数落在组,而C组中的数据是:94,90,92,
按从小到大排列为:
所以第个,第个数据为:
所以中位数为:分,
因为七年级学生成绩中分有个,出现的次数最多,所以众数分,
故答案为:a=40,b=93,c=96.
(2)八年级掌握得更好.因为七八年级的平均数、中位数相同,
而八年级的众数比七年级高,说明八年级高分的同学更多;
八年级方差比七年级小,说明八年级两极分化差距小.
(3)由题意得:七年级成绩大于或等于分的有人,八年级成绩大于或等于分的有人
(人)
答:参加此次调查活动成绩优秀的学生人数约为780人.
【点睛】本题考查的是扇形统计图,频数分布,平均数,众数,中位数,方差的含义及应用,同时考查了利用样本估计总体,掌握以上知识是解题的关键.
24.(1)详见解析;(2),;(3)详见解析
【分析】(1)根据A校选手的平均成绩可以算出总成绩,减去已知的4名选手成绩即可得到2号选手成绩,据此可以补全条形统计图;
(2)阅读条形统计图,再根据众数和平均数的意义,可以算得答案;
(3)可以分别从成绩稳定性和高分人数多少两个方面作出比较.
【详解】(1)∵
∴可以补全条形统计图如下:
(2)阅读条形统计图,发现B校5名选手成绩中,100分有两个,其他70、75、80各一个,所以B校选手成绩的众数是100分,B校选手的平均成绩=(70+75+80+100+100)÷5=85分.
故答案是;.
(3)解:∵
∴从稳定性方面考虑,两校平均成绩相等,但是A校方差较小,所以A校成绩比较稳定;
从高分人数方面考虑,B校众数为100分,A校众数为85分,100>80,所以B校高分众数多.
【点睛】本题考查数据分析指标的计算,根据公式正确计算各项指标,并作出合理分析是解题关键.
