山东省文登市第二中学2022-2023学年六年级下学期期中复习模拟训练数学试卷(含答案)
文档属性
| 名称 | 山东省文登市第二中学2022-2023学年六年级下学期期中复习模拟训练数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 219.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-02 17:06:31 | ||
图片预览


文档简介
六年级数学下册
期中复习训练卷
一、选择题(共10小题,每小题3分,共30分)
1. 小辉同学画出了如下的四个图形,你认为是五边形的是( )
2. “道路尽可能修直一点”,这是因为( )
A.两点确定一条直线 B.直线最短 C.两点之间线段最短 D.直线是无限长的
3. 下列运算正确的是( )
A.(-4ab2)2=8a2b4 B.-a6÷a3=-a3 C.2a3·a2=2a6 D.a3+a3=2a6
4. 石墨烯是目前世上最薄、最坚硬的纳米材料,同时还是导电性最好的材料,其理论厚度仅0.000 000 000 34 m.横线上的数用科学记数法可以表示为( )
A.0.34×10-9 B.3.4×10-9 C.3.4×10-10 D.3.4×10-11
5. 用度、分、秒表示30.26°为( )
A.30°26′ B.30°15′ C.30°15′36″ D.30°26″
6. 如图,点M,N为线段AB的三等分点,点C为线段NB的中点,且CM=6 cm,则AB的长度为( )
A.12 cm B.10 cm C.8 cm D.7 cm
7. 在下列计算中,不能用平方差公式计算的是( )
A.(m-n)(-m+n) B.(x3-y3)(x3+y3)
C.(-a-b)(a-b) D.(c2-d2)(d2+c2)
8. 若x2+x-2=0,那么代数式(x-6)(x+3)-2x(x-1)的值为( )
A.40 B.4 C.-18 D.-20
9. 如图,OC是∠AOD的平分线,OE是∠BOD的平分线.∠AOC=30°,∠BOD=80°,∠COE的度数为( )
A.50° B.60° C.65° D.70°
10. 已知A=-4x2,B是多项式,在计算B+A时,小马虎同学把B+A看成了B·A,结果得32x5-16x4,则B+A的值为( )
A.-8x3+4x2 B.-8x3+8x2 C.-8x3 D.x2-3x+1
二.填空题(共8小题,每小题3分,共24分)
11.计算:2m5÷m2=________.
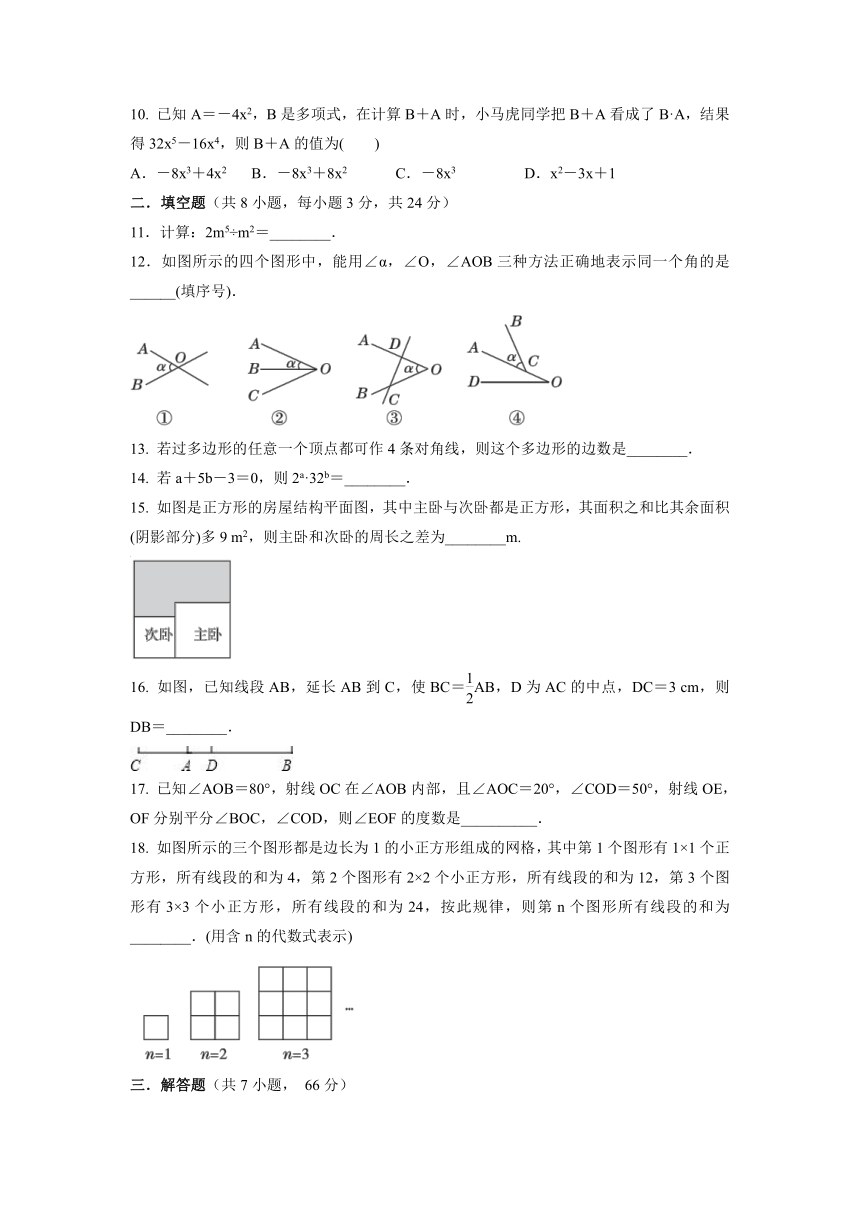
12.如图所示的四个图形中,能用∠α,∠O,∠AOB三种方法正确地表示同一个角的是______(填序号).
13. 若过多边形的任意一个顶点都可作4条对角线,则这个多边形的边数是________.
14. 若a+5b-3=0,则2a·32b=________.
15. 如图是正方形的房屋结构平面图,其中主卧与次卧都是正方形,其面积之和比其余面积(阴影部分)多9 m2,则主卧和次卧的周长之差为________m.
16. 如图,已知线段AB,延长AB到C,使BC=AB,D为AC的中点,DC=3 cm,则DB=________.
17. 已知∠AOB=80°,射线OC在∠AOB内部,且∠AOC=20°,∠COD=50°,射线OE,OF分别平分∠BOC,∠COD,则∠EOF的度数是__________.
18. 如图所示的三个图形都是边长为1的小正方形组成的网格,其中第1个图形有1×1个正方形,所有线段的和为4,第2个图形有2×2个小正方形,所有线段的和为12,第3个图形有3×3个小正方形,所有线段的和为24,按此规律,则第n个图形所有线段的和为________.(用含n的代数式表示)
三.解答题(共7小题, 66分)
19.(8分) 计算:
(1)-23+×(2 024+3)0-;
(2)(2x+3)(2x-3)-4x(x-1)+(x-2)2.
20.(8分) 已知∠A=24.1°+6°,∠B=56°-26°30′,∠C=18°12′+11.8°,试通过计算,比较∠A,∠B和∠C的大小.
21.(8分) 如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是射线OB的反向延长线.
(1)射线OC的方向是____________;
(2)若射线OE平分∠COD,求∠AOE的度数.
22.(8分) 先化简,再求值:
(1)[(a+b)2-(a-b)2]·a,其中a=-1,b=5;
(2)(x+5)(x-1)+(x-2)2,其中x=-2.
23.(10分) 如图,已知A,B,C三点在同一直线上,AB=24 cm,BC=AB,点E是AC的中点,点D是AB的中点,求DE的长.
24.(10分) 已知A=(4x4-x2)÷x2,B=(2x+5)(2x-5)+1.
(1)求A和B;
(2)若C-A=B,求C的代数式;
(3)在(2)的条件下,当C的代数式值为7时,求8x2+(8x2-C)2-30的值.
25.(14分) 如图,已知∠AOB=90°,三角形COD是含45°角的直角三角尺,OE平分∠BOC.
(1)如图①,当∠AOC=30°时,∠DOE=________°;
(2)如图②,当∠AOC=60°时,求∠DOE的度数;
(3)如图③,当∠AOC=α(90°<α<180°)时,求∠DOE的度数(用含α的式子表示);
(4)当0°<∠AOC<180°时,请直接写出∠AOC与∠DOE的数量关系.
参考答案
1-5ACBCC 6-10AADDC
11. 2m3
12. ③
13.7
14. 8
15.12
16. 1 cm
17. 5°或55°
18. 2n2+2n
19. 解 :(1)原式=-8+-9=-17+=-.
(2)原式=4x2-9-4x2+4x+x2-4x+4=x2-5.
20. 解:∠A=24.1°+6°=30.1°=30°6′,∠B=56°-26°30′=29°30′,∠C=18°12′+11.8°=18°12′+11°48′=29°60′=30°,因为30°6′>30°>29°30′,所以∠A>∠C>∠B.
21. 解:(1)北偏东70°
(2)因为∠AOC=∠AOB=55°,所以∠BOC=110°.因为射线OD是射线OB的反向延长线,所以∠BOD=180°,所以∠COD=180°-110°=70°.因为OE平分∠COD,所以∠COE=35°,所以∠AOE=∠COE+∠AOC=90°.
22. 解:(1)原式=[a2+2ab+b2-(a2-2ab+b2)]·a=(a2+2ab+b2-a2+2ab-b2)·a=4ab·a=4a2b.当a=-1,b=5时,原式=4a2b=4×(-1)2×5=20.
(2)原式=x2+4x-5+x2-4x+4=2x2-1,当x=-2时,原式=2x2-1=2×(-2)2-1=7.
23. 解:因为AB=24 cm,所以BC=AB=×24=9(cm).所以AC=AB+BC=24+9=33(cm).因为点E是AC的中点,所以AE=AC=×33=16.5(cm).因为点D是AB的中点,所以AD=AB=×24=12(cm).所以DE=AE-AD=16.5-12=4.5(cm).
24. 解:(1)A=(4x4-x2)÷x2=4x2-1,B=(2x+5)(2x-5)+1=4x2-25+1=4x2-24.
(2)由C-A=B,得到C=A+B=4x2-1+4x2-24=8x2-25.
(3)由题意知8x2-25=7,即x2=4.则原式=8×4+(8×4-7)2-30=32+625-30=627.
25. 解:(1)15
(2)因为∠AOB=90°,∠AOC=60°,所以∠BOC=∠AOB-∠AOC=30°.因为OE平分∠BOC,所以∠EOC=∠BOC=15°.因为∠COD=45°,所以∠DOE=∠COD-∠EOC=30°.
(3)因为∠AOB=90°,∠AOC=α(90°<α<180°),所以∠BOC=∠AOC-∠AOB=α-90°.因为OE平分∠BOC,所以∠EOC=∠BOC=α-45°.因为∠COD=45°,所以∠DOE=∠COD+∠EOC=α.
(4)∠AOC与∠DOE的数量关系为∠AOC=2∠DOE.
期中复习训练卷
一、选择题(共10小题,每小题3分,共30分)
1. 小辉同学画出了如下的四个图形,你认为是五边形的是( )
2. “道路尽可能修直一点”,这是因为( )
A.两点确定一条直线 B.直线最短 C.两点之间线段最短 D.直线是无限长的
3. 下列运算正确的是( )
A.(-4ab2)2=8a2b4 B.-a6÷a3=-a3 C.2a3·a2=2a6 D.a3+a3=2a6
4. 石墨烯是目前世上最薄、最坚硬的纳米材料,同时还是导电性最好的材料,其理论厚度仅0.000 000 000 34 m.横线上的数用科学记数法可以表示为( )
A.0.34×10-9 B.3.4×10-9 C.3.4×10-10 D.3.4×10-11
5. 用度、分、秒表示30.26°为( )
A.30°26′ B.30°15′ C.30°15′36″ D.30°26″
6. 如图,点M,N为线段AB的三等分点,点C为线段NB的中点,且CM=6 cm,则AB的长度为( )
A.12 cm B.10 cm C.8 cm D.7 cm
7. 在下列计算中,不能用平方差公式计算的是( )
A.(m-n)(-m+n) B.(x3-y3)(x3+y3)
C.(-a-b)(a-b) D.(c2-d2)(d2+c2)
8. 若x2+x-2=0,那么代数式(x-6)(x+3)-2x(x-1)的值为( )
A.40 B.4 C.-18 D.-20
9. 如图,OC是∠AOD的平分线,OE是∠BOD的平分线.∠AOC=30°,∠BOD=80°,∠COE的度数为( )
A.50° B.60° C.65° D.70°
10. 已知A=-4x2,B是多项式,在计算B+A时,小马虎同学把B+A看成了B·A,结果得32x5-16x4,则B+A的值为( )
A.-8x3+4x2 B.-8x3+8x2 C.-8x3 D.x2-3x+1
二.填空题(共8小题,每小题3分,共24分)
11.计算:2m5÷m2=________.
12.如图所示的四个图形中,能用∠α,∠O,∠AOB三种方法正确地表示同一个角的是______(填序号).
13. 若过多边形的任意一个顶点都可作4条对角线,则这个多边形的边数是________.
14. 若a+5b-3=0,则2a·32b=________.
15. 如图是正方形的房屋结构平面图,其中主卧与次卧都是正方形,其面积之和比其余面积(阴影部分)多9 m2,则主卧和次卧的周长之差为________m.
16. 如图,已知线段AB,延长AB到C,使BC=AB,D为AC的中点,DC=3 cm,则DB=________.
17. 已知∠AOB=80°,射线OC在∠AOB内部,且∠AOC=20°,∠COD=50°,射线OE,OF分别平分∠BOC,∠COD,则∠EOF的度数是__________.
18. 如图所示的三个图形都是边长为1的小正方形组成的网格,其中第1个图形有1×1个正方形,所有线段的和为4,第2个图形有2×2个小正方形,所有线段的和为12,第3个图形有3×3个小正方形,所有线段的和为24,按此规律,则第n个图形所有线段的和为________.(用含n的代数式表示)
三.解答题(共7小题, 66分)
19.(8分) 计算:
(1)-23+×(2 024+3)0-;
(2)(2x+3)(2x-3)-4x(x-1)+(x-2)2.
20.(8分) 已知∠A=24.1°+6°,∠B=56°-26°30′,∠C=18°12′+11.8°,试通过计算,比较∠A,∠B和∠C的大小.
21.(8分) 如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是射线OB的反向延长线.
(1)射线OC的方向是____________;
(2)若射线OE平分∠COD,求∠AOE的度数.
22.(8分) 先化简,再求值:
(1)[(a+b)2-(a-b)2]·a,其中a=-1,b=5;
(2)(x+5)(x-1)+(x-2)2,其中x=-2.
23.(10分) 如图,已知A,B,C三点在同一直线上,AB=24 cm,BC=AB,点E是AC的中点,点D是AB的中点,求DE的长.
24.(10分) 已知A=(4x4-x2)÷x2,B=(2x+5)(2x-5)+1.
(1)求A和B;
(2)若C-A=B,求C的代数式;
(3)在(2)的条件下,当C的代数式值为7时,求8x2+(8x2-C)2-30的值.
25.(14分) 如图,已知∠AOB=90°,三角形COD是含45°角的直角三角尺,OE平分∠BOC.
(1)如图①,当∠AOC=30°时,∠DOE=________°;
(2)如图②,当∠AOC=60°时,求∠DOE的度数;
(3)如图③,当∠AOC=α(90°<α<180°)时,求∠DOE的度数(用含α的式子表示);
(4)当0°<∠AOC<180°时,请直接写出∠AOC与∠DOE的数量关系.
参考答案
1-5ACBCC 6-10AADDC
11. 2m3
12. ③
13.7
14. 8
15.12
16. 1 cm
17. 5°或55°
18. 2n2+2n
19. 解 :(1)原式=-8+-9=-17+=-.
(2)原式=4x2-9-4x2+4x+x2-4x+4=x2-5.
20. 解:∠A=24.1°+6°=30.1°=30°6′,∠B=56°-26°30′=29°30′,∠C=18°12′+11.8°=18°12′+11°48′=29°60′=30°,因为30°6′>30°>29°30′,所以∠A>∠C>∠B.
21. 解:(1)北偏东70°
(2)因为∠AOC=∠AOB=55°,所以∠BOC=110°.因为射线OD是射线OB的反向延长线,所以∠BOD=180°,所以∠COD=180°-110°=70°.因为OE平分∠COD,所以∠COE=35°,所以∠AOE=∠COE+∠AOC=90°.
22. 解:(1)原式=[a2+2ab+b2-(a2-2ab+b2)]·a=(a2+2ab+b2-a2+2ab-b2)·a=4ab·a=4a2b.当a=-1,b=5时,原式=4a2b=4×(-1)2×5=20.
(2)原式=x2+4x-5+x2-4x+4=2x2-1,当x=-2时,原式=2x2-1=2×(-2)2-1=7.
23. 解:因为AB=24 cm,所以BC=AB=×24=9(cm).所以AC=AB+BC=24+9=33(cm).因为点E是AC的中点,所以AE=AC=×33=16.5(cm).因为点D是AB的中点,所以AD=AB=×24=12(cm).所以DE=AE-AD=16.5-12=4.5(cm).
24. 解:(1)A=(4x4-x2)÷x2=4x2-1,B=(2x+5)(2x-5)+1=4x2-25+1=4x2-24.
(2)由C-A=B,得到C=A+B=4x2-1+4x2-24=8x2-25.
(3)由题意知8x2-25=7,即x2=4.则原式=8×4+(8×4-7)2-30=32+625-30=627.
25. 解:(1)15
(2)因为∠AOB=90°,∠AOC=60°,所以∠BOC=∠AOB-∠AOC=30°.因为OE平分∠BOC,所以∠EOC=∠BOC=15°.因为∠COD=45°,所以∠DOE=∠COD-∠EOC=30°.
(3)因为∠AOB=90°,∠AOC=α(90°<α<180°),所以∠BOC=∠AOC-∠AOB=α-90°.因为OE平分∠BOC,所以∠EOC=∠BOC=α-45°.因为∠COD=45°,所以∠DOE=∠COD+∠EOC=α.
(4)∠AOC与∠DOE的数量关系为∠AOC=2∠DOE.
同课章节目录
