添括号[上学期]

课件18张PPT。制作： 周大兴添括号热身运动(预习）
各显身手（尝试）
更上一层楼（练习）
智力大冲浪（变式）
我们的收获…
热身运动1、复习提问：
（1）去括号法则是（2）填空：
①　a-（-b-c）=__________ ， ②　x2-y2- 4（2x2-3y2）= _________
③　a+（b-c）=___________
④　a-（b-c）=_____________a+b+cX2-y2-8x2+12y2
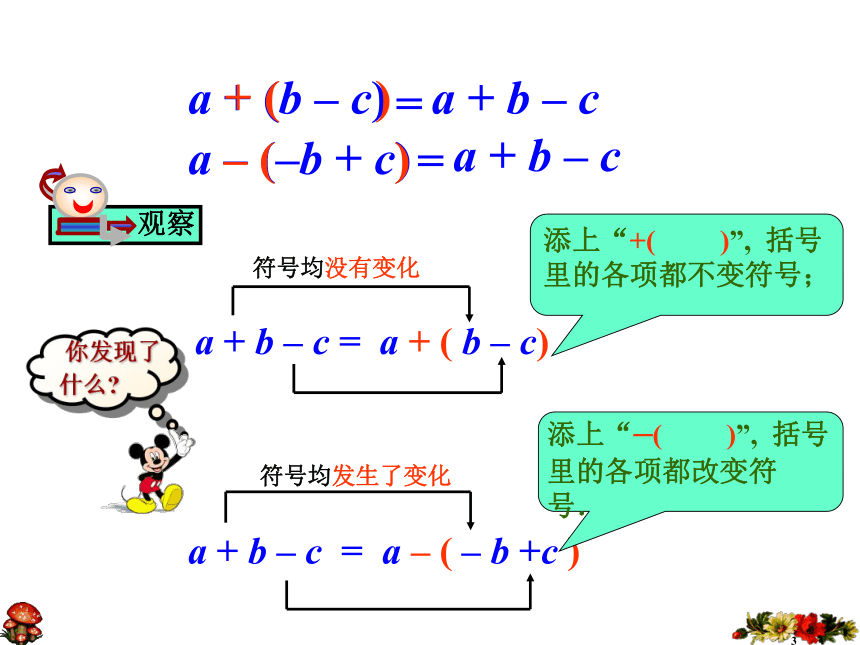
a+b-ca-b+c 热身运动 a + (b + c)a – (b +c )１．当a=6，b=2, c=3时，上面的式子成立吗？２．你还能结合实际给上面的等式作出具体的解释吗 ？3a + (b – c)a – (–b + c)a + b – c = a + ( b – c)符号均没有变化 a + b – c = a – ( – b +c )符号均发生了变化+ ( )– ( )==a + b – ca + b – c
你能根据上面的分析总结出去括号的法则吗?所添的括号前面是“+”号，括到括号里的各项都不变号；
所添的括号前面是“－”号，括到括号里的各项都要变号。 怎样检验呢？检验方法：用去括号法则来检验添括号
是否正确各显身手做一做：
1.在括号内填入适当的项：
(1) x 2–x+1 = x 2 –( )；
(2) 2 x 2–3 x–1= 2 x 2 +( )；
(3)(a–b)–(c–d)= a –( ). x–1–3x–1b + c – d2.判断下面的添括号对不对：
(1) a2+2ab+b2=a2+(2ab+b2) ( )
(2) a2 – 2ab+b2=a2 – (2ab+b2) ( )
(3) a – b – c+d=(a+d) –(b – c) ( )
(4) (a – b+c)(– a+b+c)
=[+(a – b)+c][–(a – b)+c] ( )
=[c –(– a + b)][c+(– a + b)] ( ) 各显身手√ × × √ √ 1. 用简便方法计算：
(1)214a＋47a＋53a；(2)214a – 39a – 61a．7解:(1) 214a＋47a＋53a= 214a＋(47a＋53a)= 214a＋100a= 314a(2) 214a – 39a – 61a=214a – (39a ＋ 61a)=214a – 100a=114a2. 化简求值：2x2y –3xy2 + 4x2y–5 xy2其中x＝1，y＝－1．解:2x2y –3xy2 + 4x2y–5 xy2=(2x2y + 4x2y) –(3xy2 + 5 xy2)=6x2y–8xy2当x＝1，y＝－1时原式=6×12×(–1)–8×1×( –1 )2= –6–8= –14更上一层楼1.??用简便方法计算：
(1) 117x + 138x – 38x ;
(2) 125x – 64x – 36x ;
????(3) 136x – 87x + 57x .(1) 3x2 y2 – 2 x3 + y3
(2) – a3 + 2a2 – a +1
(3) 3x2 – 2xy2 + 2y22. 给下列多项式添括号，使它们的最高次项系数为正数.如: – x2 + x = –(x2 – x); x2 – x = + (x2 – x)= +( )= –( )= –( )= –( )93x2 y2 – 2 x3 + y3a3 – 2a2 + a – 1– 3x2 + 2xy2 – 2y22xy2– 3x2 – 2y2你一定行智力大冲浪3. 填空: 2xy2 – x3 – y3 + 3x2y
=+( )
= –( )
= 2xy2 – ( )+ 3x2y
= 2xy2 + ( )+ 3x2y
= 2xy2 – ( ) – x3 2xy2 – x3 – y3 + 3x2y– 2xy2 + x3 + y3 – 3x2yx3 + y3– x3 – y3y3 – 3x2y我们的收获……结合本堂课内容，请用下列句式造句。我学会了……
我明白了……
我认为……
我会用……
我想……探索题 (1) 把多项式１０ｘ３－７ｘ２ｙ＋４ｘｙ２＋２ｙ３－５写成两个多项式的差，使被减数不含字母ｙ。1）（ 10x3-5）-（7x2y-4xy2-2y3）探索题 (2) 已知ｓ＋ｔ＝２１，３ｍ－２ｎ＝－１１求（２ｓ＋９ｍ）＋［－（６ｎ－２ｔ）］的值 原式=2s+9m-6n+2t
=2（s+t）+3（3m-2n）
=2×21+3×（-11）=9