广西钦州市2022-2023学年九年级下学期期中考试数学试卷(含答案)
文档属性
| 名称 | 广西钦州市2022-2023学年九年级下学期期中考试数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 160.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-03 10:13:46 | ||
图片预览


文档简介
广西钦州市2022-2023学年九年级下学期期中考试数学试卷
一、选择题(本大题共12小题,共60分。在每小题列出的选项中,选出符合题目的一项)
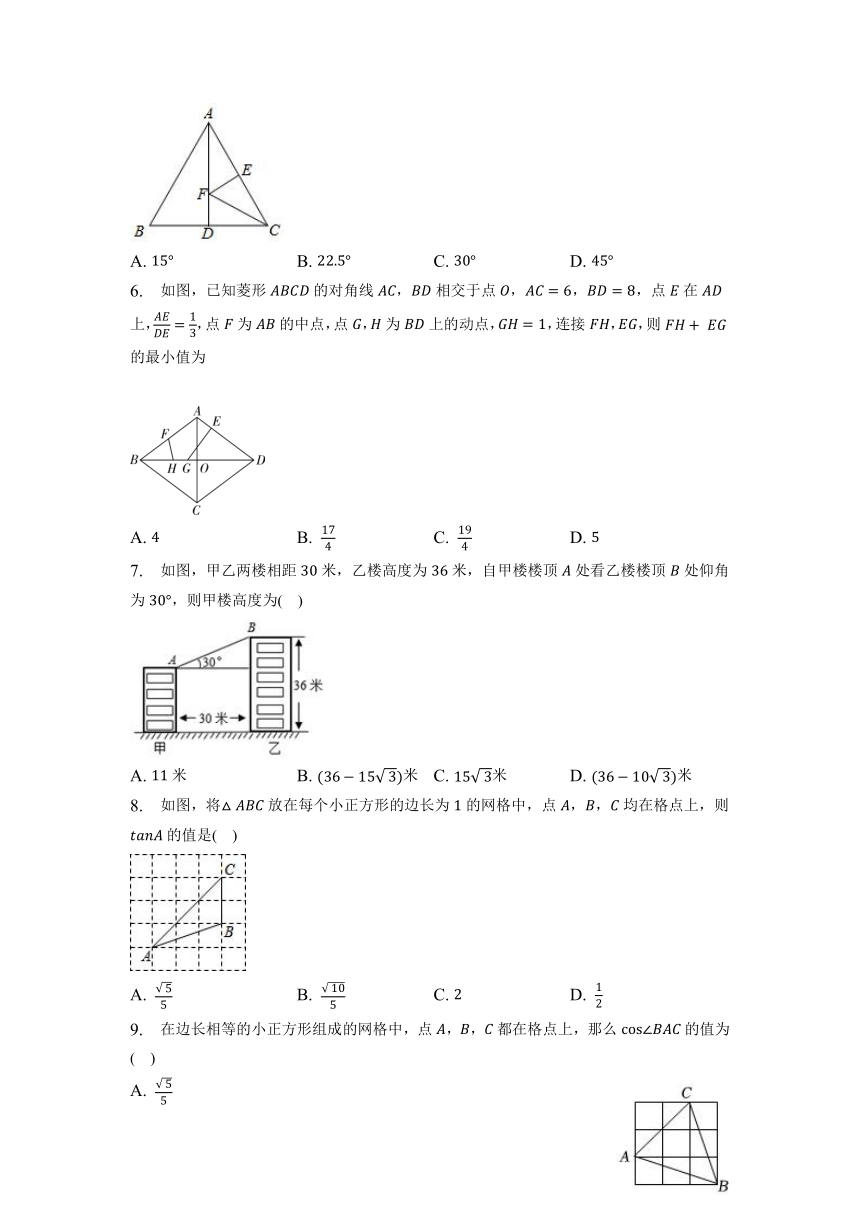
1. 如图,一块四边形绿化园地,四角都做有半径为的圆形喷水池,则这四个喷水池占去的绿化园地的面积为( )
A.
B.
C.
D.
2. 如图,矩形中,点在双曲线上,点,在轴上,延长至点,使,连接交轴于点,连接,则的面积为( )
A.
B.
C.
D.
3. 下列图形是中心对称图形,也是轴对称的是( )
A. B. C. D.
4. 如图,在一块长、宽的长方形场地上,有一条弯曲的道路,其余的部分为绿化区,道路的左边线向右平移就是它的右边线,则绿化区的面积是( )
A. B. C. D.
5. 如图,等边的边长为,是边上的中线,是边上的动点,是边上一点,若,当取得最小值时,则的度数为( )
A. B. C. D.
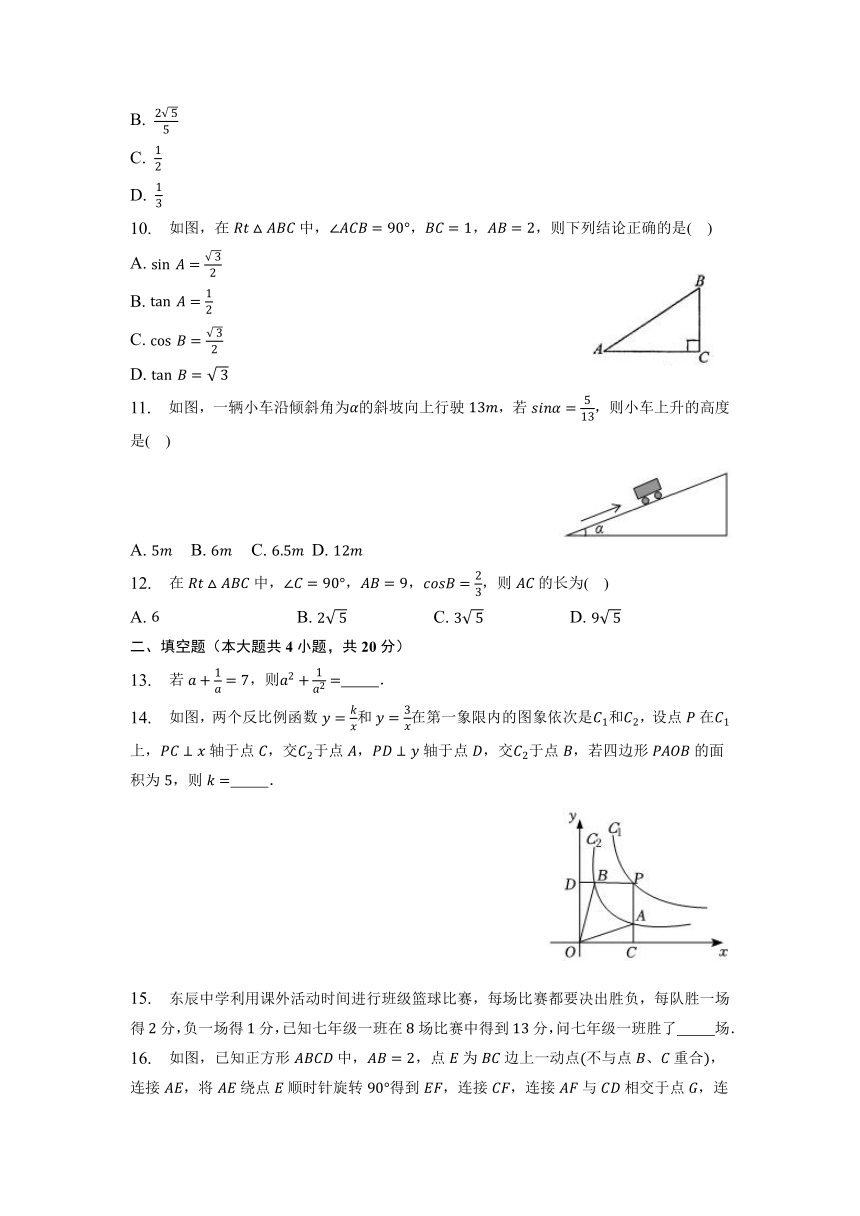
6. 如图,已知菱形的对角线,相交于点,,,点在上,,点为的中点,点,为上的动点,,连接,,则的最小值为
A. B. C. D.
7. 如图,甲乙两楼相距米,乙楼高度为米,自甲楼楼顶处看乙楼楼顶处仰角为,则甲楼高度为( )
A. 米 B. 米 C. 米 D. 米
8. 如图,将放在每个小正方形的边长为的网格中,点,,均在格点上,则的值是( )
A. B. C. D.
9. 在边长相等的小正方形组成的网格中,点,,都在格点上,那么的值为( )
A.
B.
C.
D.
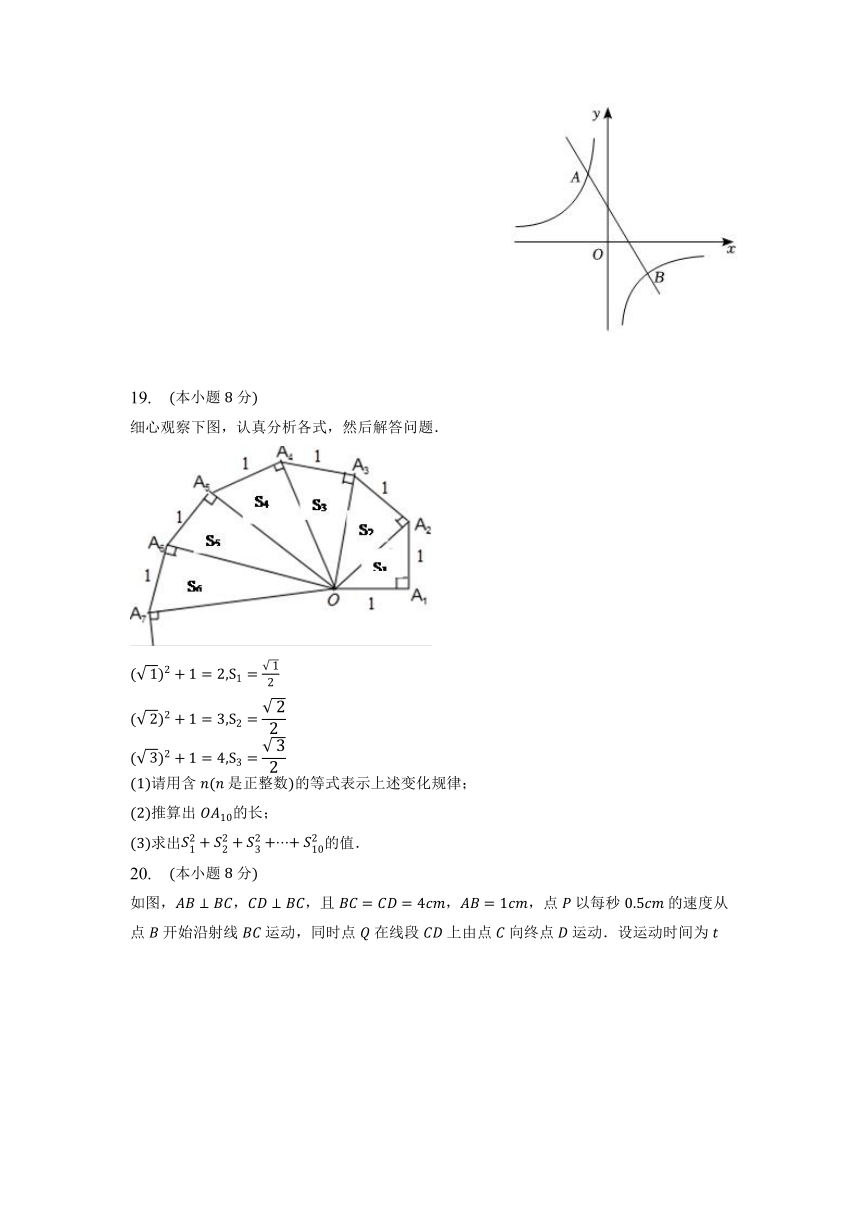
10. 如图,在中,,,,则下列结论正确的是( )
A.
B.
C.
D.
11. 如图,一辆小车沿倾斜角为的斜坡向上行驶,若,则小车上升的高度是( )
A. B. C. D.
12. 在中,,,,则的长为( )
A. B. C. D.
二、填空题(本大题共4小题,共20分)
13. 若,则 .
14. 如图,两个反比例函数和在第一象限内的图象依次是和,设点在上,轴于点,交于点,轴于点,交于点,若四边形的面积为,则 .
15. 东辰中学利用课外活动时间进行班级篮球比赛,每场比赛都要决出胜负,每队胜一场得分,负一场得分,已知七年级一班在场比赛中得到分,问七年级一班胜了 场.
16. 如图,已知正方形中,,点为边上一动点不与点、重合,连接,将绕点顺时针旋转得到,连接,连接与相交于点,连接,当最小时,四边形的面积是 .
三、解答题(本大题共5小题,共40分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
如图,和都是等腰直角三角形,,,的顶点在的斜边上,连接.
证明:≌;
当点在线段上运动时,猜想、和之间的关系,并证明.
在的运动过程中,当,时,求的面积.
18. 本小题分
如图,一次函数为常数的图象与反比例函数为常数,且的图象交于,两点,且点的坐标为.
分别求出反比例函数及一次函数的表达式;
点在轴上,当时,求点的坐标.
19. 本小题分
细心观察下图,认真分析各式,然后解答问题.
请用含是正整数的等式表示上述变化规律;
推算出的长;
求出的值.
20. 本小题分
如图,,,且,,点以每秒的速度从点开始沿射线运动,同时点在线段上由点向终点运动.设运动时间为秒.
当时,_____,_____.
如图,当点与点经过几秒时,使得与全等?此时,点的速度是多少?写出求解过程
如图,是否存在点,使得是等腰三角形?若存在,请直接写出的值, 若不存在,请说明理由.
21. 本小题分
如图所示,直线与轴交于点,与轴交于点,抛物线经过点,.
求抛物线的解析式
点在抛物线的对称轴上,求的最小值;
如图所示,是线段的上一个动点,过点垂直于轴的直线与直线和抛物线分别交于点、.
若以,,为顶点的三角形与相似,则的面积为______;
若点恰好是线段的中点,点是直线上一个动点,在坐标平面内是否存在点,使以点,,,为顶点的四边形是菱形?若存在,请直接写出点的坐标;若不存在,请说明理由.
注:二次函数的顶点坐标为
参考答案
1. 2. 3. 4. 5. 6. 7.
8. 9. 10. 11. 12.
13. 14. 15. 16.
17.证明:和都是等腰直角三角形,
,
,即
在和中,
,
≌;
.
证明:作交于点,
,
故设,设,则,,
是等腰直角三角形,
,
,
是直角三角形,
由勾股定理可得:,
,,,
;
解:作交于点,
,,是等腰直角三角形,
,
,
,
,
,
在中,,
即,
,
作交于点,
,,
,
,
,
故设,则,
,
,解得:,
.
18.解:两函数图象相交于点,
,,
解得,,
反比例函数的表达式为,
一次函数的表达式为;
联立,
解得舍去,,
所以,点的坐标为,
设,则有,
或,
或.
19.解:, 是正整数;
,
;
.
20.解:,;
若使与全等,需分两种情况:
当且时,,
解得,此时,
点的速度为,
当且时,,
解得,此时,
点的速度为,
综上所述,若使得与全等,点和点经过秒,此时点的速度为;或点和点经过秒,此时点的速度为;
或或或.
21.解:将代入,
,
将和代入,
,
抛物线解析式为;
作点关于抛物线的对称轴直线的对称点,连,交直线于点.
连,此时的值最小.
抛物线对称轴为直线,
,
由勾股定理,
的最小值为;
或;
存在.
设坐标为,
则为,
则点坐标为,
把点坐标代入,解得舍去,,
当时,点在垂直平分线上,则,
当时,由菱形性质点坐标为,
当时,、关于直线对称,点坐标为.
一、选择题(本大题共12小题,共60分。在每小题列出的选项中,选出符合题目的一项)
1. 如图,一块四边形绿化园地,四角都做有半径为的圆形喷水池,则这四个喷水池占去的绿化园地的面积为( )
A.
B.
C.
D.
2. 如图,矩形中,点在双曲线上,点,在轴上,延长至点,使,连接交轴于点,连接,则的面积为( )
A.
B.
C.
D.
3. 下列图形是中心对称图形,也是轴对称的是( )
A. B. C. D.
4. 如图,在一块长、宽的长方形场地上,有一条弯曲的道路,其余的部分为绿化区,道路的左边线向右平移就是它的右边线,则绿化区的面积是( )
A. B. C. D.
5. 如图,等边的边长为,是边上的中线,是边上的动点,是边上一点,若,当取得最小值时,则的度数为( )
A. B. C. D.
6. 如图,已知菱形的对角线,相交于点,,,点在上,,点为的中点,点,为上的动点,,连接,,则的最小值为
A. B. C. D.
7. 如图,甲乙两楼相距米,乙楼高度为米,自甲楼楼顶处看乙楼楼顶处仰角为,则甲楼高度为( )
A. 米 B. 米 C. 米 D. 米
8. 如图,将放在每个小正方形的边长为的网格中,点,,均在格点上,则的值是( )
A. B. C. D.
9. 在边长相等的小正方形组成的网格中,点,,都在格点上,那么的值为( )
A.
B.
C.
D.
10. 如图,在中,,,,则下列结论正确的是( )
A.
B.
C.
D.
11. 如图,一辆小车沿倾斜角为的斜坡向上行驶,若,则小车上升的高度是( )
A. B. C. D.
12. 在中,,,,则的长为( )
A. B. C. D.
二、填空题(本大题共4小题,共20分)
13. 若,则 .
14. 如图,两个反比例函数和在第一象限内的图象依次是和,设点在上,轴于点,交于点,轴于点,交于点,若四边形的面积为,则 .
15. 东辰中学利用课外活动时间进行班级篮球比赛,每场比赛都要决出胜负,每队胜一场得分,负一场得分,已知七年级一班在场比赛中得到分,问七年级一班胜了 场.
16. 如图,已知正方形中,,点为边上一动点不与点、重合,连接,将绕点顺时针旋转得到,连接,连接与相交于点,连接,当最小时,四边形的面积是 .
三、解答题(本大题共5小题,共40分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
如图,和都是等腰直角三角形,,,的顶点在的斜边上,连接.
证明:≌;
当点在线段上运动时,猜想、和之间的关系,并证明.
在的运动过程中,当,时,求的面积.
18. 本小题分
如图,一次函数为常数的图象与反比例函数为常数,且的图象交于,两点,且点的坐标为.
分别求出反比例函数及一次函数的表达式;
点在轴上,当时,求点的坐标.
19. 本小题分
细心观察下图,认真分析各式,然后解答问题.
请用含是正整数的等式表示上述变化规律;
推算出的长;
求出的值.
20. 本小题分
如图,,,且,,点以每秒的速度从点开始沿射线运动,同时点在线段上由点向终点运动.设运动时间为秒.
当时,_____,_____.
如图,当点与点经过几秒时,使得与全等?此时,点的速度是多少?写出求解过程
如图,是否存在点,使得是等腰三角形?若存在,请直接写出的值, 若不存在,请说明理由.
21. 本小题分
如图所示,直线与轴交于点,与轴交于点,抛物线经过点,.
求抛物线的解析式
点在抛物线的对称轴上,求的最小值;
如图所示,是线段的上一个动点,过点垂直于轴的直线与直线和抛物线分别交于点、.
若以,,为顶点的三角形与相似,则的面积为______;
若点恰好是线段的中点,点是直线上一个动点,在坐标平面内是否存在点,使以点,,,为顶点的四边形是菱形?若存在,请直接写出点的坐标;若不存在,请说明理由.
注:二次函数的顶点坐标为
参考答案
1. 2. 3. 4. 5. 6. 7.
8. 9. 10. 11. 12.
13. 14. 15. 16.
17.证明:和都是等腰直角三角形,
,
,即
在和中,
,
≌;
.
证明:作交于点,
,
故设,设,则,,
是等腰直角三角形,
,
,
是直角三角形,
由勾股定理可得:,
,,,
;
解:作交于点,
,,是等腰直角三角形,
,
,
,
,
,
在中,,
即,
,
作交于点,
,,
,
,
,
故设,则,
,
,解得:,
.
18.解:两函数图象相交于点,
,,
解得,,
反比例函数的表达式为,
一次函数的表达式为;
联立,
解得舍去,,
所以,点的坐标为,
设,则有,
或,
或.
19.解:, 是正整数;
,
;
.
20.解:,;
若使与全等,需分两种情况:
当且时,,
解得,此时,
点的速度为,
当且时,,
解得,此时,
点的速度为,
综上所述,若使得与全等,点和点经过秒,此时点的速度为;或点和点经过秒,此时点的速度为;
或或或.
21.解:将代入,
,
将和代入,
,
抛物线解析式为;
作点关于抛物线的对称轴直线的对称点,连,交直线于点.
连,此时的值最小.
抛物线对称轴为直线,
,
由勾股定理,
的最小值为;
或;
存在.
设坐标为,
则为,
则点坐标为,
把点坐标代入,解得舍去,,
当时,点在垂直平分线上,则,
当时,由菱形性质点坐标为,
当时,、关于直线对称,点坐标为.
同课章节目录
