8.4.2空间点、直线、平面之间的位置关系+教案-2022-2023学年高一下学期数学人教A版(2019)必修第二册
文档属性
| 名称 | 8.4.2空间点、直线、平面之间的位置关系+教案-2022-2023学年高一下学期数学人教A版(2019)必修第二册 |  | |
| 格式 | docx | ||
| 文件大小 | 307.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-01 18:57:09 | ||
图片预览

文档简介
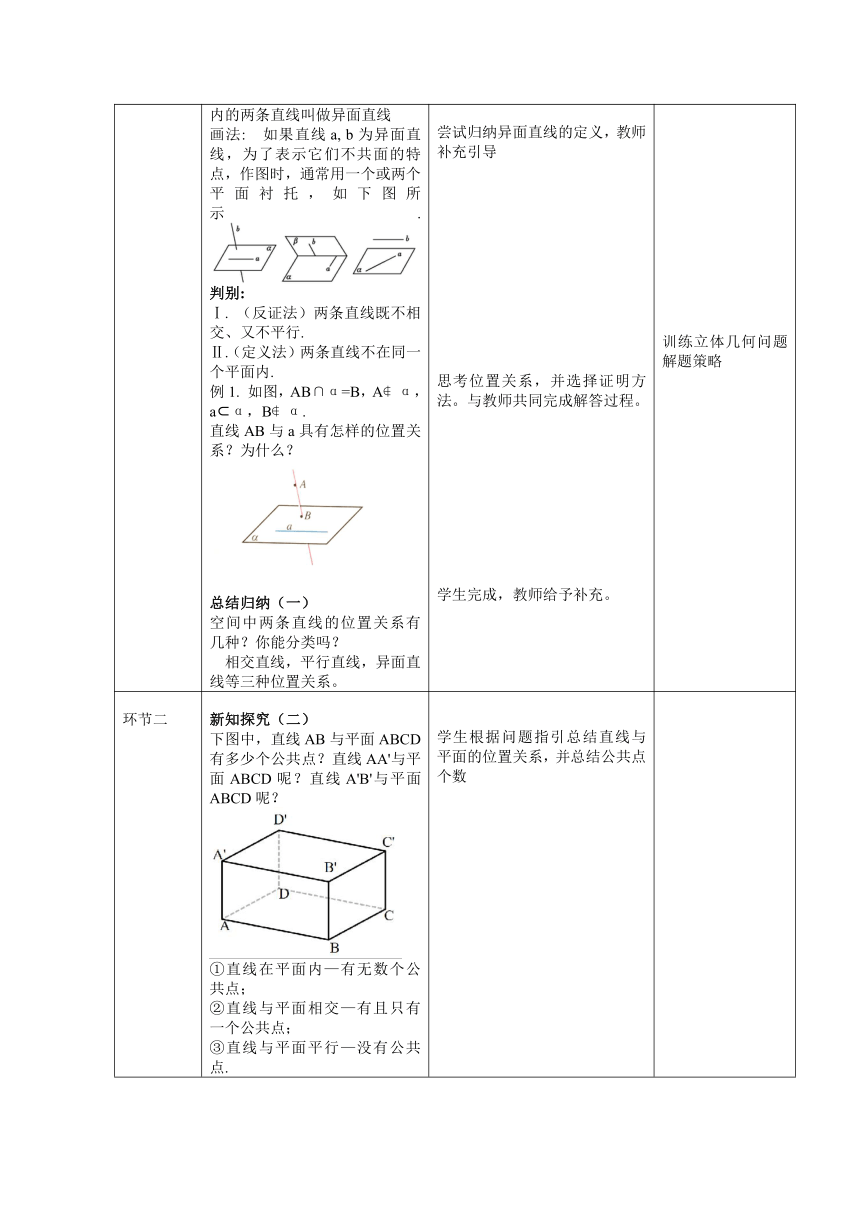
学科:数学 授课年级:高一 教学题目:空间点,直线,平面之间的位置关系
学时 一课时
课标要求 借助长方体,从构成立体图形的基本元素----点.线.面入手,研究他们的性质以及他们之间的相互关系,特别是对直线与平面的平行和垂直的关系展开研究。
内容与学情分析 内容分析 1. 空间中直线与直线的位置关系 2. 空间中直线与平面的位置关系 3. 空间中平面与平面的位置关系
学习重点
学习难点
学情分析 提示:学生学习本节课时的心理状态、已有的知识储备和学习准备情况。以此作为解决教学重点、难点和选择教学策略、设计教学过程的依据。
学习目标 1.了解直线与直线之间、直线与平面、平面与平面之间的位置关系; 2.会用图形语言和符号语言表示空间点、直线、平面之间的位置关系; 3.掌握异面直线的含义,并会判断其位置关系。
学生课前需要做的准备工作 提示:包括需要预习的内容,思考的问题,调查收集的资料等。
学习策略 提示:学习模式、学习方法
学习 环节 学习任务设计与教师活动 学生活动设计 设计意图 落实目标
导入新课 复习导入:1.回顾8.4.1我们讲过的内容,回答下面问题。 2.前面我们认识了空间中点、线、面之间的一些位置关系,如点在平面内,直线在平面内,两个平面相较,等等。空间中点、直线、平面之间还有其他位置关系吗?长方体是我们熟悉的空间几何体,下面我们借助长方体进一步研究空间中点、直线、平面之间的位置关系。 回顾旧知,引出新知。
环节一 学习任务与学习目标相对应 新知探究(一) 直线与直线的位置关系如何? ①平面中直线与直线的位置关系有几种? ②空间中直线与直线的位置关系有几种?观察长方体,思考长方体的棱与棱之间有没有平行与相交的位置关系?你能找出例子进行说明吗?你还能在长方体中找到其它类型的位置关系吗? 异面直线 定义:我们把不同在任何一平面内的两条直线叫做异面直线 画法: 如果直线a, b为异面直线,为了表示它们不共面的特点,作图时,通常用一个或两个平面衬托,如下图所示. 判别: Ⅰ. (反证法)两条直线既不相交、又不平行. Ⅱ.(定义法)两条直线不在同一个平面内. 例1. 如图,AB∩α=B,A α,a α,B α. 直线AB与a具有怎样的位置关系?为什么? 总结归纳(一) 空间中两条直线的位置关系有几种?你能分类吗? 相交直线,平行直线,异面直线等三种位置关系。 观察长方体回答问题 尝试归纳异面直线的定义,教师补充引导 思考位置关系,并选择证明方法。与教师共同完成解答过程。 学生完成,教师给予补充。 加强空间想象能力与探究能力; 加强总结归纳能力 训练立体几何问题解题策略
环节二 (
a
l
A
B
) 新知探究(二) 下图中,直线AB与平面ABCD有多少个公共点?直线AA'与平面ABCD呢?直线A'B'与平面ABCD呢? ①直线在平面内—有无数个公共点; ②直线与平面相交—有且只有一个公共点; ③直线与平面平行—没有公共点. 直线在平面内 (
A
α
a
) 直线与平面相交 直线与平面平行 例2 用符号表示下列图形中点、直线、平面之间的位置关系. 总结归纳(二) 2. 空间中直线与平面的位置关系 学生根据问题指引总结直线与平面的位置关系,并总结公共点个数
(
B
D
C
A'
B'
C'
D'
A
)环节三 学习任务与学习目标相对应 新知探究(三) 下图中,平面ABCD与平面A'B'C'D'有多少个公共点?平面ABCD与平面BCC'B'呢? ①两个平面平行——没有公共点; ②两个平面相交——有一条公共直线. 注意:画两个平面平行时,通常画两个对应边互相平行的平行四边形. 总结归纳(三) 3. 空间中平面与平面的位置关系
达标 检测 作业 (
1. 判断下列命题是否正确,正确的在括号内画“√”,错误的画“×”.
(1) 若直线l上有无数个点不在平面α内,则l // α.( )
(2) 若直线l与平面α平行,则l与平面α内的任意一条直线都平行.( )
(3) 如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行.( )
(4)若直线l与平面α平行,则l与平面α内的任意一条直线都没有公共点.( )
P131-1.(1)若两条直线a与b没有公共点,那么a与b( )
A.共面 B.平行
C.是异面直线
D.可能平行,也可能是异面直线
P131-1.(2)设直线a与b分别是长方体相邻两个面的对角线所在的直线,则a与b( )
A.平行 B.相交
C.是异面直线
D.可能相交,也可能是异面直线
P132-3.判断正误:
直线a α,b β,则a,b是异面直线.( )
直线a α,b β,α//β,则a //b.( )
) 梳理总结 1. 空间中直线与直线的位置关系 相交直线:在同一平面内,有且只有一个公共点; 共面直线 异面直线:在同一平面内,没有公共点; 异面直线:不同在任何一个平面内,没有公共点. 2. 空间中直线与平面的位置关系 ①直线在平面内—有无数个公共点; ②直线与平面相交—有且只有一个公共点; ③直线与平面平行—没有公共点. 空间中平面与平面的位置关系 ①两个平面平行——没有公共点; ②两个平面相交——有一条公共直线.
板书 设计 要求:重点突出,内容完整,逻辑性强,符合视觉心理,便于学生学习。
学时 一课时
课标要求 借助长方体,从构成立体图形的基本元素----点.线.面入手,研究他们的性质以及他们之间的相互关系,特别是对直线与平面的平行和垂直的关系展开研究。
内容与学情分析 内容分析 1. 空间中直线与直线的位置关系 2. 空间中直线与平面的位置关系 3. 空间中平面与平面的位置关系
学习重点
学习难点
学情分析 提示:学生学习本节课时的心理状态、已有的知识储备和学习准备情况。以此作为解决教学重点、难点和选择教学策略、设计教学过程的依据。
学习目标 1.了解直线与直线之间、直线与平面、平面与平面之间的位置关系; 2.会用图形语言和符号语言表示空间点、直线、平面之间的位置关系; 3.掌握异面直线的含义,并会判断其位置关系。
学生课前需要做的准备工作 提示:包括需要预习的内容,思考的问题,调查收集的资料等。
学习策略 提示:学习模式、学习方法
学习 环节 学习任务设计与教师活动 学生活动设计 设计意图 落实目标
导入新课 复习导入:1.回顾8.4.1我们讲过的内容,回答下面问题。 2.前面我们认识了空间中点、线、面之间的一些位置关系,如点在平面内,直线在平面内,两个平面相较,等等。空间中点、直线、平面之间还有其他位置关系吗?长方体是我们熟悉的空间几何体,下面我们借助长方体进一步研究空间中点、直线、平面之间的位置关系。 回顾旧知,引出新知。
环节一 学习任务与学习目标相对应 新知探究(一) 直线与直线的位置关系如何? ①平面中直线与直线的位置关系有几种? ②空间中直线与直线的位置关系有几种?观察长方体,思考长方体的棱与棱之间有没有平行与相交的位置关系?你能找出例子进行说明吗?你还能在长方体中找到其它类型的位置关系吗? 异面直线 定义:我们把不同在任何一平面内的两条直线叫做异面直线 画法: 如果直线a, b为异面直线,为了表示它们不共面的特点,作图时,通常用一个或两个平面衬托,如下图所示. 判别: Ⅰ. (反证法)两条直线既不相交、又不平行. Ⅱ.(定义法)两条直线不在同一个平面内. 例1. 如图,AB∩α=B,A α,a α,B α. 直线AB与a具有怎样的位置关系?为什么? 总结归纳(一) 空间中两条直线的位置关系有几种?你能分类吗? 相交直线,平行直线,异面直线等三种位置关系。 观察长方体回答问题 尝试归纳异面直线的定义,教师补充引导 思考位置关系,并选择证明方法。与教师共同完成解答过程。 学生完成,教师给予补充。 加强空间想象能力与探究能力; 加强总结归纳能力 训练立体几何问题解题策略
环节二 (
a
l
A
B
) 新知探究(二) 下图中,直线AB与平面ABCD有多少个公共点?直线AA'与平面ABCD呢?直线A'B'与平面ABCD呢? ①直线在平面内—有无数个公共点; ②直线与平面相交—有且只有一个公共点; ③直线与平面平行—没有公共点. 直线在平面内 (
A
α
a
) 直线与平面相交 直线与平面平行 例2 用符号表示下列图形中点、直线、平面之间的位置关系. 总结归纳(二) 2. 空间中直线与平面的位置关系 学生根据问题指引总结直线与平面的位置关系,并总结公共点个数
(
B
D
C
A'
B'
C'
D'
A
)环节三 学习任务与学习目标相对应 新知探究(三) 下图中,平面ABCD与平面A'B'C'D'有多少个公共点?平面ABCD与平面BCC'B'呢? ①两个平面平行——没有公共点; ②两个平面相交——有一条公共直线. 注意:画两个平面平行时,通常画两个对应边互相平行的平行四边形. 总结归纳(三) 3. 空间中平面与平面的位置关系
达标 检测 作业 (
1. 判断下列命题是否正确,正确的在括号内画“√”,错误的画“×”.
(1) 若直线l上有无数个点不在平面α内,则l // α.( )
(2) 若直线l与平面α平行,则l与平面α内的任意一条直线都平行.( )
(3) 如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行.( )
(4)若直线l与平面α平行,则l与平面α内的任意一条直线都没有公共点.( )
P131-1.(1)若两条直线a与b没有公共点,那么a与b( )
A.共面 B.平行
C.是异面直线
D.可能平行,也可能是异面直线
P131-1.(2)设直线a与b分别是长方体相邻两个面的对角线所在的直线,则a与b( )
A.平行 B.相交
C.是异面直线
D.可能相交,也可能是异面直线
P132-3.判断正误:
直线a α,b β,则a,b是异面直线.( )
直线a α,b β,α//β,则a //b.( )
) 梳理总结 1. 空间中直线与直线的位置关系 相交直线:在同一平面内,有且只有一个公共点; 共面直线 异面直线:在同一平面内,没有公共点; 异面直线:不同在任何一个平面内,没有公共点. 2. 空间中直线与平面的位置关系 ①直线在平面内—有无数个公共点; ②直线与平面相交—有且只有一个公共点; ③直线与平面平行—没有公共点. 空间中平面与平面的位置关系 ①两个平面平行——没有公共点; ②两个平面相交——有一条公共直线.
板书 设计 要求:重点突出,内容完整,逻辑性强,符合视觉心理,便于学生学习。
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
