河北省邯郸市魏县第五中学2022-2023学年高一下学期数学五一作业(立体几何初步)(含答案)
文档属性
| 名称 | 河北省邯郸市魏县第五中学2022-2023学年高一下学期数学五一作业(立体几何初步)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-01 19:08:16 | ||
图片预览



文档简介
魏县第五中学2022-2023学年高一下学期五一作业
立体几何初步
一、单选题
1.在四面体中,,,,,则该四面体外接球的表面积是
A. B. C. D.
2.棱长为的正方体中,是面的中心,则到平面的距离是( )
A. B. C. D.
3.扇子,作为中华民族文化的代表产物,在我国已经有四、五千年的历史了.折扇出现铰晚,因可折叠,方便随身携带,流传最广,经研究发现采用黄金分割方式设计的折扇(将一个圆面按黄金分割比例进行分割后得到的较小扇形)最为美观和实用,已知一把黄金分割扇的半径为,则以此扇面围成的圆锥的体积为( )
A. B. C. D.
4.一个封闭的圆柱形容器,内部装有高度为三分之一的水(图一),将容器歪倒放在水平放置的的桌面上,设水面截底面得到的弦所对的圆心角为,则( )
A. B. C. D.
5.已知是边长为3的等边三角形,三棱锥全部顶点都在表面积为的球O的球面上,则三棱锥的体积的最大值为( ).
A. B. C. D.
6.三棱柱中,棱、、两两垂直,,且三棱柱的侧面积为.若该三棱柱的顶点都在同一个球的表面上,则球表面积的最小值为( )
A. B. C. D.
7.如图,在直三棱柱中,、分别为、的中点,将此三棱柱沿、、截出一个棱锥,则棱锥的体积与剩下几何体体积的比值是( )
A. B. C. D.
8.某同学制作了一个对面图案均相同的正方形礼品盒,如图所示,则这个正方体礼品盒的表面展开图应该为(对面是相同的图案)( )
A. B. C. D.
二、多选题
9.已知m,n是空间中两条不同的直线,,为空间中两个互相垂直的平面,则下列命题不正确的是( )
A.若,则 B.若,,则
C.若,,则 D.若,,则
10.已知的三边长分别是,,.则下列说法正确的是( )
A.以所在直线为旋转轴,将此三角形旋转一周,所得旋转体的侧面积为
B.以所在直线为旋转轴,将此三角形旋转一周,所得旋转体的体积为
C.以所在直线为旋转轴,将此三角形旋转一周,所得旋转体的全面积为
D.以所在直线为旋转轴,将此三角形旋转一周,所得旋转体的体积为
11.在三棱锥中,已知,,,平面平面ABC,且,则( ).
A.
B.平面平面ABC
C.三棱锥的体积为
D.三棱锥的外接球的表面积为
12.如图,在棱长为2的正方体中为上的动点,则( )
A.三棱锥的体积为
B.对任意点平面
C.线段长度的最小值为2
D.设与平面所成角的大小为,则
三、填空题
13.如图所示为一个半圆柱,已知为半圆弧上一点,若,,直线与所成角的正切值为,则点到平面的距离是______.
14.半球的表面积与其内最大正方体的表面积之比为______.
15.在正方体中,则异面直线与的夹角为_________.
16.已知一个球的体积为,则它的俯视图的面积为______.
四、解答题
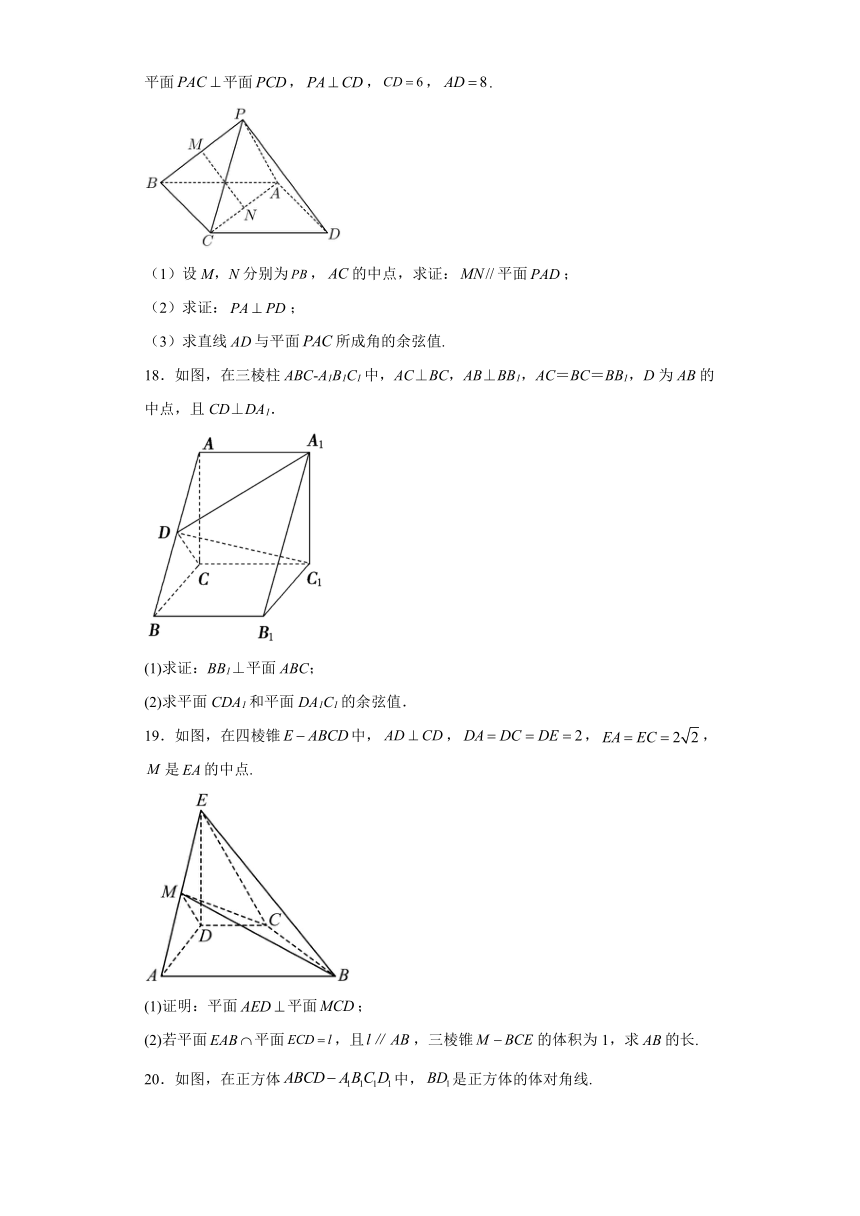
17.如图,在四棱锥中,底面为平行四边形,为等边三角形,平面平面,,,.
(1)设M,N分别为,的中点,求证:平面;
(2)求证:;
(3)求直线与平面所成角的余弦值.
18.如图,在三棱柱ABC A1B1C1中,AC⊥BC,AB⊥BB1,AC=BC=BB1,D为AB的中点,且CD⊥DA1.
(1)求证:BB1⊥平面ABC;
(2)求平面CDA1和平面DA1C1的余弦值.
19.如图,在四棱锥中,,,,是的中点.
(1)证明:平面平面;
(2)若平面平面,且,三棱锥的体积为1,求的长.
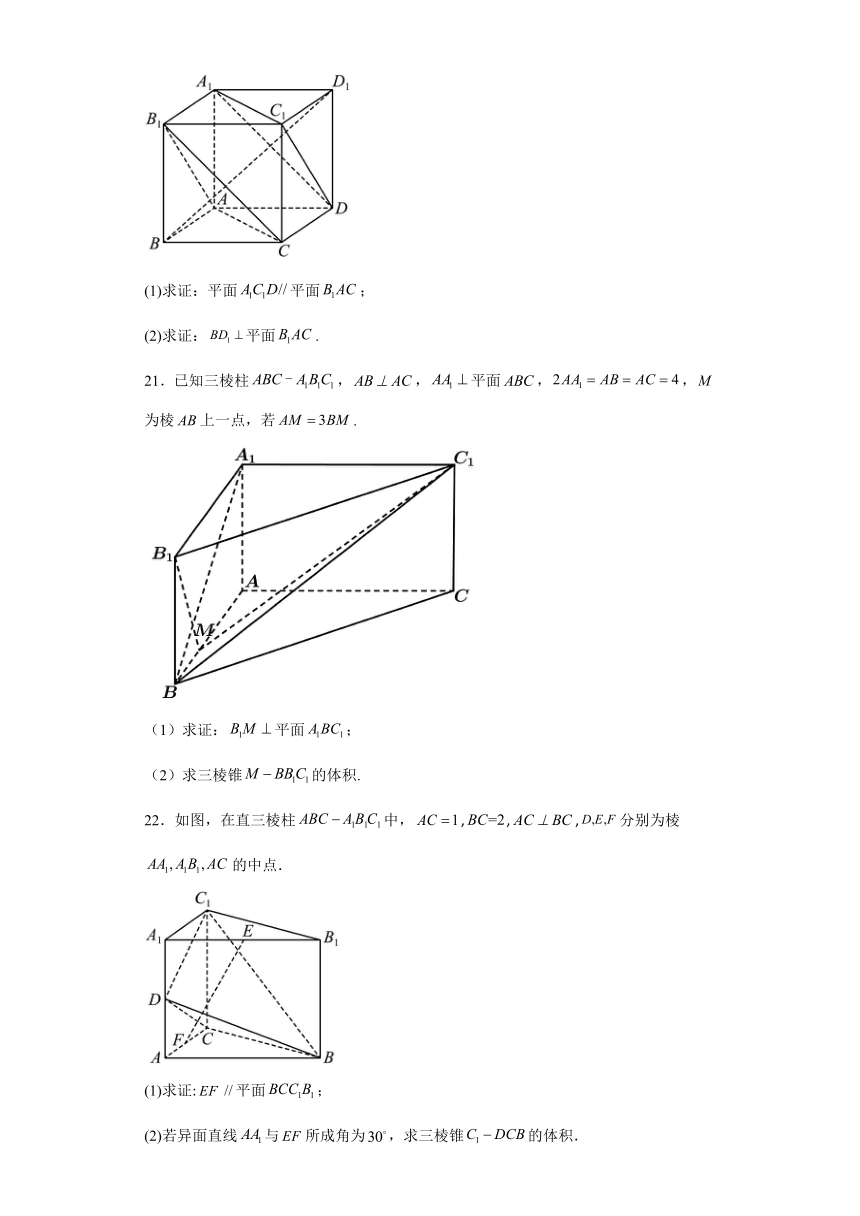
20.如图,在正方体中,是正方体的体对角线.
(1)求证:平面平面;
(2)求证:平面.
21.已知三棱柱,,平面,,为棱上一点,若.
(1)求证:平面;
(2)求三棱锥的体积.
22.如图,在直三棱柱中,,,,分别为棱的中点.
(1)求证:平面;
(2)若异面直线与所成角为,求三棱锥的体积.
参考答案:
1.D 2.B 3.B 4.D 5.C 6.C 7.C 8.A
9.ABD 10.ABD 11.ABC 12.ABD
13.
14.
15.
16..
17.(1)连接,易知,,又,故,
又因为平面,平面,所以平面.
(2)取棱的中点H,连换,又为等边三角形,所以,又因为平面平面,平面平面,所以平面,
又平面,所以,又已知,,
所以平面,又平面,所以,
(3)连接,由(2)中平面,
可得为直线与平面所成的角.
因为为等边三角形,,且H为的中点,所以,
又,
故在中,,,
又,所以直线与平面所成角的余弦值为.
18.(1)证明:由是中点,得,又,,平面,
所以平面,而平面,所以,
因为,,平面,所以平面;
(2)解:由已知及(1)可得CB,CC1,CA两两互相垂直,所以以C为坐标原点,以CB所在直线为x轴,CC1所在直线为y轴,CA所在直线为z轴建立如图所示空间直角坐标系,设CC1=2,则C(0,0,0),C1(0,2,0),A1(0,2,2),D(1,0,1),所以=(1,0,1),=(0,2,2),=(1,-2,1),=(0,0,2).
设平面DCA1的法向量=(x1,y1,z1),则即令z1=-1,则x1=1,y1=1,=(1,1,-1).
设平面DC1A1的法向量=(x2,y2,z2),则即得z2=0,x2-2y2=0,令y2=1,则x2=2,=(2,1,0).
所以cos〈,〉===.
故平面CDA1和平面DA1C1所成角余弦值为.
19.(1)∵,,∴,
又∵,∴为等边三角形,
又∵,是的中点,
∴,,,
又∵,,平面,∴平面,
平面,平面平面;
(2)因为平面平面,所以平面,
又,平面
所以平面,又平面,平面平面,
所以,
∵平面,∴,
又∵,,平面,
∴平面,又∵平面,
∴,∵,∴,
又∵,,,平面,∴平面,
∵,∴点到平面的距离等于点到平面的距离,
∴,
又∵,
解得.
20.(1)证明:在正方体中,且,且,
所以四边形、为平行四边,
所以,,
因为平面,平面,所以平面,
因为平面,平面,所以平面,
又,平面,平面,
所以平面平面.
(2)证明:连接、,在正方体中,,
平面,
因为平面,
所以,
又,平面,所以平面,
又平面,所以,
同理可证平面,又平面,所以,
又,平面,
所以平面,
又平面平面,所以平面.
21.(1)平面,平面,
所以,又,
所以平面,
平面,所以,
所以,
在和有:,
可得,
所以 ,,
所以平面,得证;
(2)
.
22.(1)取的中点,连接,
因为分别为棱的中点,所以,,
平面平面,
平面,同理可证平面,
且,平面,
所以平面平面,
又平面,所以平面;
(2)由(1)知为异面直线与所成角,所以,
因为三棱柱为直三棱柱,所以平面,
因为,所以平面,又平面,
,又,在中,,
,
,,平面,
平面,
所以
立体几何初步
一、单选题
1.在四面体中,,,,,则该四面体外接球的表面积是
A. B. C. D.
2.棱长为的正方体中,是面的中心,则到平面的距离是( )
A. B. C. D.
3.扇子,作为中华民族文化的代表产物,在我国已经有四、五千年的历史了.折扇出现铰晚,因可折叠,方便随身携带,流传最广,经研究发现采用黄金分割方式设计的折扇(将一个圆面按黄金分割比例进行分割后得到的较小扇形)最为美观和实用,已知一把黄金分割扇的半径为,则以此扇面围成的圆锥的体积为( )
A. B. C. D.
4.一个封闭的圆柱形容器,内部装有高度为三分之一的水(图一),将容器歪倒放在水平放置的的桌面上,设水面截底面得到的弦所对的圆心角为,则( )
A. B. C. D.
5.已知是边长为3的等边三角形,三棱锥全部顶点都在表面积为的球O的球面上,则三棱锥的体积的最大值为( ).
A. B. C. D.
6.三棱柱中,棱、、两两垂直,,且三棱柱的侧面积为.若该三棱柱的顶点都在同一个球的表面上,则球表面积的最小值为( )
A. B. C. D.
7.如图,在直三棱柱中,、分别为、的中点,将此三棱柱沿、、截出一个棱锥,则棱锥的体积与剩下几何体体积的比值是( )
A. B. C. D.
8.某同学制作了一个对面图案均相同的正方形礼品盒,如图所示,则这个正方体礼品盒的表面展开图应该为(对面是相同的图案)( )
A. B. C. D.
二、多选题
9.已知m,n是空间中两条不同的直线,,为空间中两个互相垂直的平面,则下列命题不正确的是( )
A.若,则 B.若,,则
C.若,,则 D.若,,则
10.已知的三边长分别是,,.则下列说法正确的是( )
A.以所在直线为旋转轴,将此三角形旋转一周,所得旋转体的侧面积为
B.以所在直线为旋转轴,将此三角形旋转一周,所得旋转体的体积为
C.以所在直线为旋转轴,将此三角形旋转一周,所得旋转体的全面积为
D.以所在直线为旋转轴,将此三角形旋转一周,所得旋转体的体积为
11.在三棱锥中,已知,,,平面平面ABC,且,则( ).
A.
B.平面平面ABC
C.三棱锥的体积为
D.三棱锥的外接球的表面积为
12.如图,在棱长为2的正方体中为上的动点,则( )
A.三棱锥的体积为
B.对任意点平面
C.线段长度的最小值为2
D.设与平面所成角的大小为,则
三、填空题
13.如图所示为一个半圆柱,已知为半圆弧上一点,若,,直线与所成角的正切值为,则点到平面的距离是______.
14.半球的表面积与其内最大正方体的表面积之比为______.
15.在正方体中,则异面直线与的夹角为_________.
16.已知一个球的体积为,则它的俯视图的面积为______.
四、解答题
17.如图,在四棱锥中,底面为平行四边形,为等边三角形,平面平面,,,.
(1)设M,N分别为,的中点,求证:平面;
(2)求证:;
(3)求直线与平面所成角的余弦值.
18.如图,在三棱柱ABC A1B1C1中,AC⊥BC,AB⊥BB1,AC=BC=BB1,D为AB的中点,且CD⊥DA1.
(1)求证:BB1⊥平面ABC;
(2)求平面CDA1和平面DA1C1的余弦值.
19.如图,在四棱锥中,,,,是的中点.
(1)证明:平面平面;
(2)若平面平面,且,三棱锥的体积为1,求的长.
20.如图,在正方体中,是正方体的体对角线.
(1)求证:平面平面;
(2)求证:平面.
21.已知三棱柱,,平面,,为棱上一点,若.
(1)求证:平面;
(2)求三棱锥的体积.
22.如图,在直三棱柱中,,,,分别为棱的中点.
(1)求证:平面;
(2)若异面直线与所成角为,求三棱锥的体积.
参考答案:
1.D 2.B 3.B 4.D 5.C 6.C 7.C 8.A
9.ABD 10.ABD 11.ABC 12.ABD
13.
14.
15.
16..
17.(1)连接,易知,,又,故,
又因为平面,平面,所以平面.
(2)取棱的中点H,连换,又为等边三角形,所以,又因为平面平面,平面平面,所以平面,
又平面,所以,又已知,,
所以平面,又平面,所以,
(3)连接,由(2)中平面,
可得为直线与平面所成的角.
因为为等边三角形,,且H为的中点,所以,
又,
故在中,,,
又,所以直线与平面所成角的余弦值为.
18.(1)证明:由是中点,得,又,,平面,
所以平面,而平面,所以,
因为,,平面,所以平面;
(2)解:由已知及(1)可得CB,CC1,CA两两互相垂直,所以以C为坐标原点,以CB所在直线为x轴,CC1所在直线为y轴,CA所在直线为z轴建立如图所示空间直角坐标系,设CC1=2,则C(0,0,0),C1(0,2,0),A1(0,2,2),D(1,0,1),所以=(1,0,1),=(0,2,2),=(1,-2,1),=(0,0,2).
设平面DCA1的法向量=(x1,y1,z1),则即令z1=-1,则x1=1,y1=1,=(1,1,-1).
设平面DC1A1的法向量=(x2,y2,z2),则即得z2=0,x2-2y2=0,令y2=1,则x2=2,=(2,1,0).
所以cos〈,〉===.
故平面CDA1和平面DA1C1所成角余弦值为.
19.(1)∵,,∴,
又∵,∴为等边三角形,
又∵,是的中点,
∴,,,
又∵,,平面,∴平面,
平面,平面平面;
(2)因为平面平面,所以平面,
又,平面
所以平面,又平面,平面平面,
所以,
∵平面,∴,
又∵,,平面,
∴平面,又∵平面,
∴,∵,∴,
又∵,,,平面,∴平面,
∵,∴点到平面的距离等于点到平面的距离,
∴,
又∵,
解得.
20.(1)证明:在正方体中,且,且,
所以四边形、为平行四边,
所以,,
因为平面,平面,所以平面,
因为平面,平面,所以平面,
又,平面,平面,
所以平面平面.
(2)证明:连接、,在正方体中,,
平面,
因为平面,
所以,
又,平面,所以平面,
又平面,所以,
同理可证平面,又平面,所以,
又,平面,
所以平面,
又平面平面,所以平面.
21.(1)平面,平面,
所以,又,
所以平面,
平面,所以,
所以,
在和有:,
可得,
所以 ,,
所以平面,得证;
(2)
.
22.(1)取的中点,连接,
因为分别为棱的中点,所以,,
平面平面,
平面,同理可证平面,
且,平面,
所以平面平面,
又平面,所以平面;
(2)由(1)知为异面直线与所成角,所以,
因为三棱柱为直三棱柱,所以平面,
因为,所以平面,又平面,
,又,在中,,
,
,,平面,
平面,
所以
同课章节目录
