合并同类项[上学期]

课件17张PPT。合并同类项初一数学组温故知新1、什么叫同类项？举例说明。2、用字母表示乘法分配律。3、下列各题能利用乘法分配律计算吗？
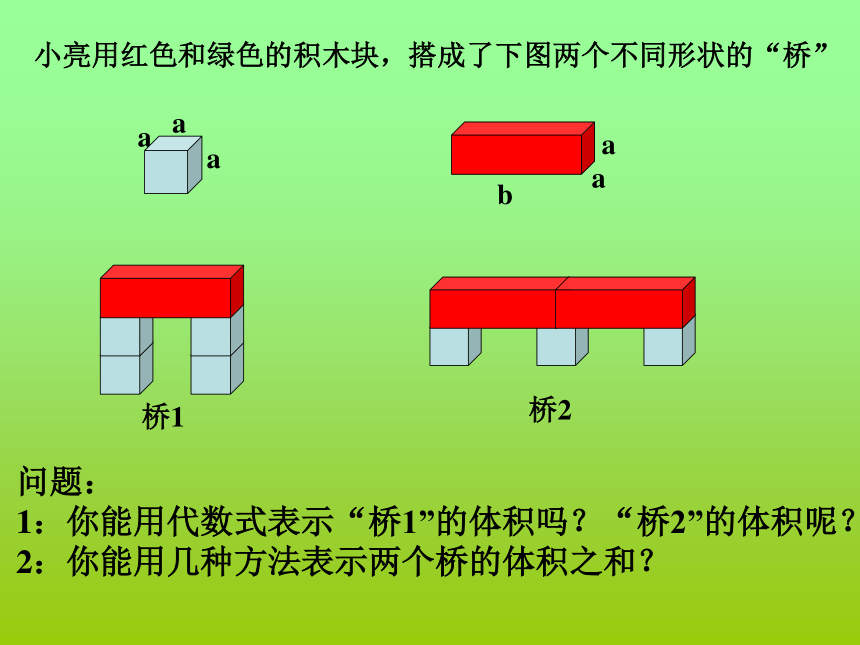
（1）（2）小亮用红色和绿色的积木块，搭成了下图两个不同形状的“桥”a桥1桥2问题：
1：你能用代数式表示“桥1”的体积吗？“桥2”的体积呢？
2：你能用几种方法表示两个桥的体积之和？4a3+a2b+3a3+2a2b=7a3+3a2b观察那些项合到一起了?4a3+3a3=7a3 a2b+2a2b=3a2b概括：
把多项式中的同类项合并成一项,叫做合并同类项。
探究大家谈谈：
1：在多项式中，某两项具有什么特点时可以合并成一项？
合并前后的系数有什么关系？
字母和它的指数有无变化？
2：把具有以上特点的两项合并成一项时，我们实际上用了
什么运算律？合并同类项法则:
把同类项的系数相加,所得的结果作为系数,字母和字母的指数保持不变。
填空：
1、2x+5x=———；
2、mn-0.5mn=———— ；
3、a+2a+3a=———；
4、-10p2q+10qp2=——；7x0.5mn6a0试一试： 化简多项式3x2y - 4xy2- 3 + 5x2y + 2xy2 +5﹏﹏=3x2y+5x2y-4xy2+2xy2-3+5=（3x2y+5x2y）+（-4xy2+2xy2 ）+（3+5）=（3+5）x2y+（-4+2）xy2+（-3+5）=8x2y-2xy2+2合并下列各题中的同类项：（2）、a3-a2b+ab2+a2b-ab2+b3大显身手合并下列各题中的同类项2、6a2-5b2+2ab+5b2-6a2例2 求多项式3x2+4x-2x2-x+x2-3x-1的值 , 其中x=-3. 解法( 一)
解:3x2+4x-2x2-x+x2-3x-1 :
=(3-2+1)x2+(4-1-3)x-1
=2x2-1
当 x=-3 时
原式 =2x(-3)2-1=17
解法(二)
当x=-3时
=3×(-3)2+4×(-3)-2×(-3)2-(-3)+(-3)2-3×(-3)-1
=3×9+(-12)-2×9+3+9+9-1
=27-12-18+3+9+9-1
=17
3x2+4x-2x2-x+x2-3x-1 求多项式
2x2-3xy+y2-xy-2x2+5xy+1的值,
其中x=2, y=-1
模拟练兵小结:合并同类项具体做法;
1.准确找出同类项,用不同记号标出来。
2.逆用分配律,把同类项的系数加在一起(用小括号,括号之间用“+”号连接,字母和字母的指数不变).
3.写出合并后的结果.
口诀同类项,须判断; 两相同,是条件;
合并时,须计算; 系数加,两不变。更上一层楼 一.判断：
1. 3a+2b=5ab,
2. 5y2-2y2=3
3. 2a3+5a2=7a5
4. 3x+2=5xy
5. 3a2b-2ba2=a2b 二.选择:1.合并同类项就是( )
A.把相同的项合并. B.把系数相加.
C.把各项合并成一项. D.把同类项合并成一项.
2.若多项式-4x3-2mx2+2x2-6中不含x2项,则m满足( )
A. m=-1 B. m≠-1 c. m=1 D. m≠1
3.将(x +y)+2(x+y)-4(x+y)合并同类项等于( )
A.X+Y, B.-(X+Y), C.-X+Y, D.X-Y.
4.长方形的长是 3a+2b,宽是 4a+b,则周长是( )
A.14a+6b, B.7a+3b, c.10a+10b, D.12a+8bDCBA思维拓展有这样一道题:
求多项式 a3b3-0.5ab2+b2-2a3b3+0.5ab2+b2+a3b3-2b2-3
的值,其中a=2.3, b=-0.25.
有一个同学指出:题目中的条件 a=2.3, b=-0.25是多余的,他的说法有无道理,用你所学的知识加以说明。