人教版八年级下册 19.2.2 一次函数 同步练习(含答案)
文档属性
| 名称 | 人教版八年级下册 19.2.2 一次函数 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 456.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-03 11:42:34 | ||
图片预览


文档简介
19.2.2 一次函数 同步练习
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1.下列一次函数中,y随x的增大而减小的是( )
A.y=x﹣3 B.y=1﹣x C.y=2x D.y=3x+2
2.一次函数的图象经过点P(a,b)和Q(c,d),则a(c-d)-b(c-d)的值为( )
A.9 B.16 C.25 D.36
3.若,则函数的图象可能是( )
A. B. C. D.
4.对于正比例函数,当自变量的值每增加时,的值就减少,则的值为( )
A. B. C. D.
5.已知关于的一次函数的图象经过第二、三、四象限,则的取值范围为( )
A. B. C. D.
6.在平面直角坐标系中,将直线平移后得到直线,则下列平移方法正确的是( )
A.将向上平移4个单位长度 B.将向下平移6个单位长度
C.将向左平移3个单位长度 D.将向右平移3个单位长度
7.若直线y=kx+k﹣1经过点(m,n+3)和(m+1,2n﹣1),且0<k<2,则n的取值范围是( )
A.0<n<2 B.0<n<4 C.2<n<6 D.4<n<6
8.如图所示,直线y=x+2分别与x轴、y轴交于点A、B,以线段AB为边,在第二象限内作等腰直角△ABC,∠BAC=90°,则过B、C两点直线的解析式为( )
A. B. C. D.y=﹣2x+2
9.如图,一束光线从点出发,经y轴上的点C反射后经过点,则点C的坐标是( )
A. B. C. D.
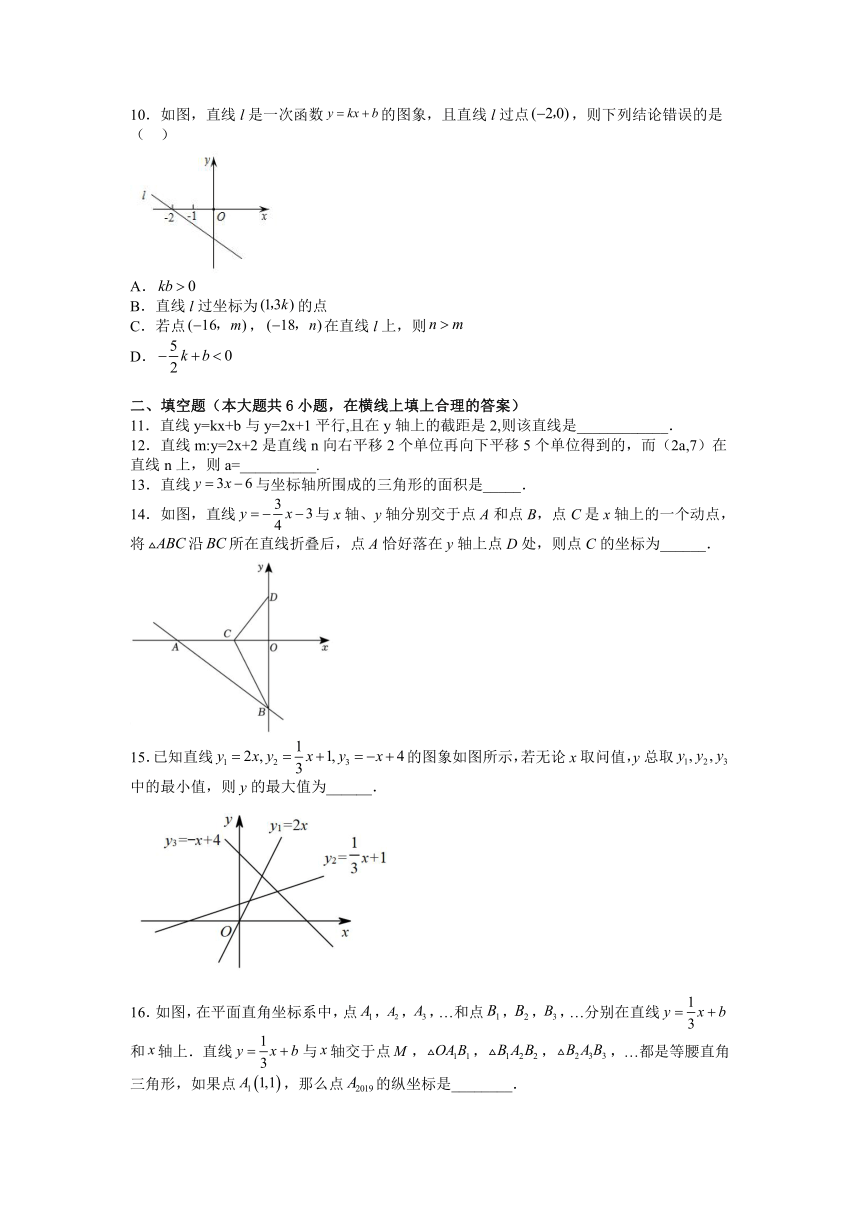
10.如图,直线l是一次函数的图象,且直线l过点,则下列结论错误的是( )
A.
B.直线l过坐标为的点
C.若点,在直线l上,则
D.
二、填空题(本大题共6小题,在横线上填上合理的答案)
11.直线y=kx+b与y=2x+1平行,且在y轴上的截距是2,则该直线是____________.
12.直线m:y=2x+2是直线n向右平移2个单位再向下平移5个单位得到的,而(2a,7)在直线n上,则a=__________.
13.直线与坐标轴所围成的三角形的面积是_____.
14.如图,直线与x轴、y轴分别交于点A和点B,点C是x轴上的一个动点,将沿所在直线折叠后,点A恰好落在y轴上点D处,则点C的坐标为______.
15.已知直线的图象如图所示,若无论x取问值,y总取中的最小值,则y的最大值为______.
16.如图,在平面直角坐标系中,点,,,…和点,,,…分别在直线和轴上.直线与轴交于点,,,,…都是等腰直角三角形,如果点,那么点的纵坐标是________.
三、解答题(本大题共5小题,解答应写出文字说明,证明过程或演算步骤)
17.在平面直角坐标系中,已知点C(m+2,3m﹣1),直线l经过点A(2,2),B(1,3).
(1)求直线l的解析式;
(2)若A,B,C三点共线,求m的值;
(3)若将直线l先沿y轴向上平移2个单位,再沿x轴向右平移3个单位后经过点C,求点C的坐标.
18.八年级(1)班张山同学利用所学函数知识,对函数进行了如下研究:
列表如下:
x … 0 1 2 3 …
y … 7 5 3 m 1 n 1 1 1 …
描点并连线(如下图)
(1)自变量x的取值范围是________;
(2)表格中:________,________;
(3)在给出的坐标系中画出函数的图象;
(4)一次函数的图象与函数的图象交点的坐标为_______.
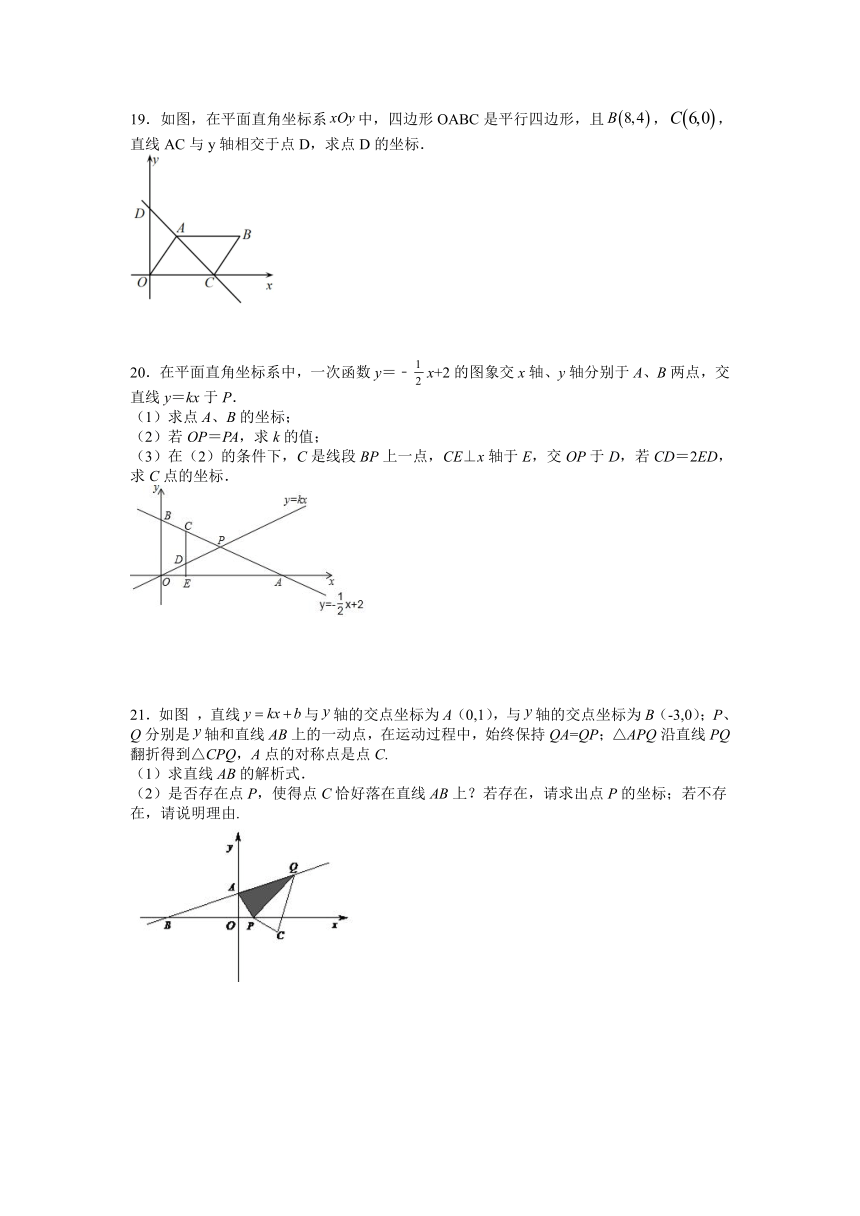
19.如图,在平面直角坐标系中,四边形OABC是平行四边形,且,,直线AC与y轴相交于点D,求点D的坐标.
20.在平面直角坐标系中,一次函数y=﹣x+2的图象交x轴、y轴分别于A、B两点,交直线y=kx于P.
(1)求点A、B的坐标;
(2)若OP=PA,求k的值;
(3)在(2)的条件下,C是线段BP上一点,CE⊥x轴于E,交OP于D,若CD=2ED,求C点的坐标.
21.如图 ,直线与轴的交点坐标为A(0,1),与轴的交点坐标为B(-3,0);P、Q分别是轴和直线AB上的一动点,在运动过程中,始终保持QA=QP;△APQ沿直线PQ翻折得到△CPQ,A点的对称点是点C.
(1)求直线AB的解析式.
(2)是否存在点P,使得点C恰好落在直线AB上?若存在,请求出点P的坐标;若不存在,请说明理由.
答案:
1.B 2.C 3.D 4.D 5.C 6.C 7.D 8.B 9.D 10.D
11.y=2x+2 12.-1 13.6 14. 15. 16.
17.(1)解:设直线解析式为:,
由题意可得:,
解得:,
直线的解析式为;
(2)解:,,三点共线,
,
解得;
(3)解:由直线l先沿y轴向上平移2个单位,再沿x轴向右平移3个单位后可得函数解析式为:,
∴把点C(m+2,3m﹣1)代入得:,
解得:,
∴点C的坐标为.
18.解:(1)∵函数y=|x+2|-x-1
∴自变量x的取值范围为全体实数
故答案为全体实数;
(2)当x=-2时,m=|-2+2|+2-1=1,
当x=0时,n=|0+2|-0-1=1,
∴
故答案为1,1;
(3)如下图
(4)在(3)中坐标系中作出直线y=-x+3,如下:
由图象得:一次函数y=-x+3的图象与函数y=|x+2|-x-1的图象交点的坐标为:(-6,9)和(2,1)
故答案为(-6,9)和(2,1).
19.解:∵四边形OABC是平行四边形,
∴AB∥OC,AB=OC,
∵B(8,4),C(6,0),
∴A(2,4),
设直线AC的解析式为y=kx+b,
∴,
解得:,
∴直线AC的解析式为y=﹣x+6,
当x=0时,y=6
∴点D的坐标为(0,6)
20.(1)对于
当时,,则点B的坐标为
当时,,解得,则点A的坐标为;
(2)∵
∴是等腰三角形
点P的横坐标为
当时,
∴点P的坐标为
∵点P在直线上
∴
解得;
(3)设点C的坐标为,则点D的坐标为,点E的坐标为
∴,
∵
∴
解得
则
故点C的坐标为.
21.(1)设直线AB的解析式为,则
解得,
即
(2)分三种情况考虑下
第一种情况(如图甲):
设P的坐标为(t,0)
∵△APQ与△CPQ关于直线PQ对称,并且点A,Q,C共线,
∴∠AQP=∠CQP=90°,
∵QA=QP,
∴QA=QP=QC
即△AQP, △CQP都是等腰直角三角形,
∴△APC是以P为顶角的等腰直角三角形.
根据AAS可以得到△AOP≌△PHC,
∴CH=OP=t,PH=OA=1,
∴点C的坐标为(t+1,t).
∵点C落在直线AB上,
∴,解得.即P的坐标为(2,0).
第二种情况(如图乙):设P的坐标为(t,0)
∵△APQ与△CPQ关于直线PQ对称,并且点A,Q,C共线,
∴∠AQP=∠CQP=90°,
∵QA=QP,∴QA=QP=QC,
即△AQP, △CQP都是等腰直角三角形,
∴△APC是以P为顶角的等腰直角三角形.
根据AAS可以得到△AOP≌△PHC,
∴CH=OP=-t,PH=OA=1,
∴点C的坐标为(t-1,-t).
∵点C落在直线AB上,∴,解得.
即P的坐标为(,0).
第三种情况(如图丙):
当点P与点B重合时,Q恰好是线段AB的中点,此时点A关于直线PQ的对称点C与点A重合,但A,P,Q三点共线,不能构成三角形,故不符合题意.
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1.下列一次函数中,y随x的增大而减小的是( )
A.y=x﹣3 B.y=1﹣x C.y=2x D.y=3x+2
2.一次函数的图象经过点P(a,b)和Q(c,d),则a(c-d)-b(c-d)的值为( )
A.9 B.16 C.25 D.36
3.若,则函数的图象可能是( )
A. B. C. D.
4.对于正比例函数,当自变量的值每增加时,的值就减少,则的值为( )
A. B. C. D.
5.已知关于的一次函数的图象经过第二、三、四象限,则的取值范围为( )
A. B. C. D.
6.在平面直角坐标系中,将直线平移后得到直线,则下列平移方法正确的是( )
A.将向上平移4个单位长度 B.将向下平移6个单位长度
C.将向左平移3个单位长度 D.将向右平移3个单位长度
7.若直线y=kx+k﹣1经过点(m,n+3)和(m+1,2n﹣1),且0<k<2,则n的取值范围是( )
A.0<n<2 B.0<n<4 C.2<n<6 D.4<n<6
8.如图所示,直线y=x+2分别与x轴、y轴交于点A、B,以线段AB为边,在第二象限内作等腰直角△ABC,∠BAC=90°,则过B、C两点直线的解析式为( )
A. B. C. D.y=﹣2x+2
9.如图,一束光线从点出发,经y轴上的点C反射后经过点,则点C的坐标是( )
A. B. C. D.
10.如图,直线l是一次函数的图象,且直线l过点,则下列结论错误的是( )
A.
B.直线l过坐标为的点
C.若点,在直线l上,则
D.
二、填空题(本大题共6小题,在横线上填上合理的答案)
11.直线y=kx+b与y=2x+1平行,且在y轴上的截距是2,则该直线是____________.
12.直线m:y=2x+2是直线n向右平移2个单位再向下平移5个单位得到的,而(2a,7)在直线n上,则a=__________.
13.直线与坐标轴所围成的三角形的面积是_____.
14.如图,直线与x轴、y轴分别交于点A和点B,点C是x轴上的一个动点,将沿所在直线折叠后,点A恰好落在y轴上点D处,则点C的坐标为______.
15.已知直线的图象如图所示,若无论x取问值,y总取中的最小值,则y的最大值为______.
16.如图,在平面直角坐标系中,点,,,…和点,,,…分别在直线和轴上.直线与轴交于点,,,,…都是等腰直角三角形,如果点,那么点的纵坐标是________.
三、解答题(本大题共5小题,解答应写出文字说明,证明过程或演算步骤)
17.在平面直角坐标系中,已知点C(m+2,3m﹣1),直线l经过点A(2,2),B(1,3).
(1)求直线l的解析式;
(2)若A,B,C三点共线,求m的值;
(3)若将直线l先沿y轴向上平移2个单位,再沿x轴向右平移3个单位后经过点C,求点C的坐标.
18.八年级(1)班张山同学利用所学函数知识,对函数进行了如下研究:
列表如下:
x … 0 1 2 3 …
y … 7 5 3 m 1 n 1 1 1 …
描点并连线(如下图)
(1)自变量x的取值范围是________;
(2)表格中:________,________;
(3)在给出的坐标系中画出函数的图象;
(4)一次函数的图象与函数的图象交点的坐标为_______.
19.如图,在平面直角坐标系中,四边形OABC是平行四边形,且,,直线AC与y轴相交于点D,求点D的坐标.
20.在平面直角坐标系中,一次函数y=﹣x+2的图象交x轴、y轴分别于A、B两点,交直线y=kx于P.
(1)求点A、B的坐标;
(2)若OP=PA,求k的值;
(3)在(2)的条件下,C是线段BP上一点,CE⊥x轴于E,交OP于D,若CD=2ED,求C点的坐标.
21.如图 ,直线与轴的交点坐标为A(0,1),与轴的交点坐标为B(-3,0);P、Q分别是轴和直线AB上的一动点,在运动过程中,始终保持QA=QP;△APQ沿直线PQ翻折得到△CPQ,A点的对称点是点C.
(1)求直线AB的解析式.
(2)是否存在点P,使得点C恰好落在直线AB上?若存在,请求出点P的坐标;若不存在,请说明理由.
答案:
1.B 2.C 3.D 4.D 5.C 6.C 7.D 8.B 9.D 10.D
11.y=2x+2 12.-1 13.6 14. 15. 16.
17.(1)解:设直线解析式为:,
由题意可得:,
解得:,
直线的解析式为;
(2)解:,,三点共线,
,
解得;
(3)解:由直线l先沿y轴向上平移2个单位,再沿x轴向右平移3个单位后可得函数解析式为:,
∴把点C(m+2,3m﹣1)代入得:,
解得:,
∴点C的坐标为.
18.解:(1)∵函数y=|x+2|-x-1
∴自变量x的取值范围为全体实数
故答案为全体实数;
(2)当x=-2时,m=|-2+2|+2-1=1,
当x=0时,n=|0+2|-0-1=1,
∴
故答案为1,1;
(3)如下图
(4)在(3)中坐标系中作出直线y=-x+3,如下:
由图象得:一次函数y=-x+3的图象与函数y=|x+2|-x-1的图象交点的坐标为:(-6,9)和(2,1)
故答案为(-6,9)和(2,1).
19.解:∵四边形OABC是平行四边形,
∴AB∥OC,AB=OC,
∵B(8,4),C(6,0),
∴A(2,4),
设直线AC的解析式为y=kx+b,
∴,
解得:,
∴直线AC的解析式为y=﹣x+6,
当x=0时,y=6
∴点D的坐标为(0,6)
20.(1)对于
当时,,则点B的坐标为
当时,,解得,则点A的坐标为;
(2)∵
∴是等腰三角形
点P的横坐标为
当时,
∴点P的坐标为
∵点P在直线上
∴
解得;
(3)设点C的坐标为,则点D的坐标为,点E的坐标为
∴,
∵
∴
解得
则
故点C的坐标为.
21.(1)设直线AB的解析式为,则
解得,
即
(2)分三种情况考虑下
第一种情况(如图甲):
设P的坐标为(t,0)
∵△APQ与△CPQ关于直线PQ对称,并且点A,Q,C共线,
∴∠AQP=∠CQP=90°,
∵QA=QP,
∴QA=QP=QC
即△AQP, △CQP都是等腰直角三角形,
∴△APC是以P为顶角的等腰直角三角形.
根据AAS可以得到△AOP≌△PHC,
∴CH=OP=t,PH=OA=1,
∴点C的坐标为(t+1,t).
∵点C落在直线AB上,
∴,解得.即P的坐标为(2,0).
第二种情况(如图乙):设P的坐标为(t,0)
∵△APQ与△CPQ关于直线PQ对称,并且点A,Q,C共线,
∴∠AQP=∠CQP=90°,
∵QA=QP,∴QA=QP=QC,
即△AQP, △CQP都是等腰直角三角形,
∴△APC是以P为顶角的等腰直角三角形.
根据AAS可以得到△AOP≌△PHC,
∴CH=OP=-t,PH=OA=1,
∴点C的坐标为(t-1,-t).
∵点C落在直线AB上,∴,解得.
即P的坐标为(,0).
第三种情况(如图丙):
当点P与点B重合时,Q恰好是线段AB的中点,此时点A关于直线PQ的对称点C与点A重合,但A,P,Q三点共线,不能构成三角形,故不符合题意.
