中位线

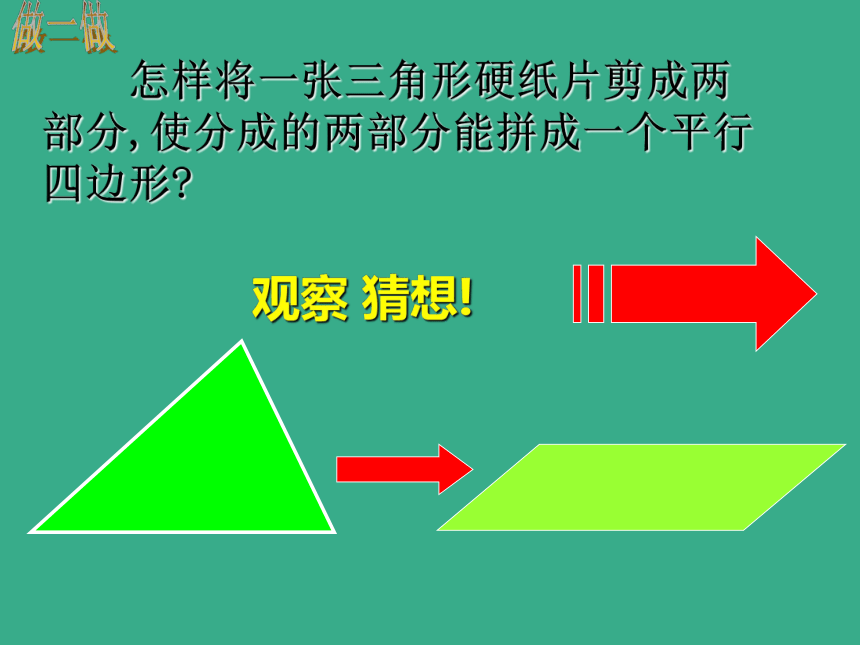
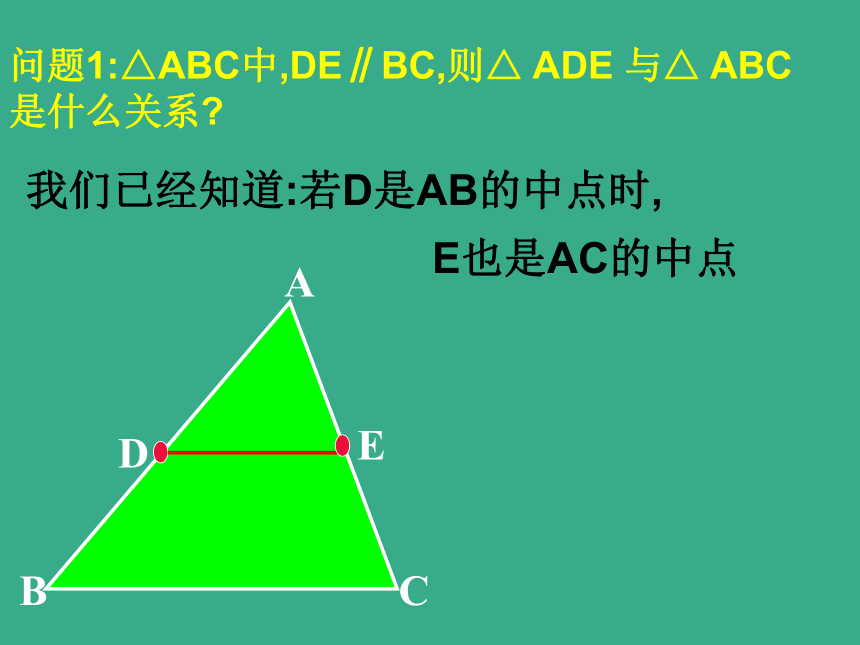
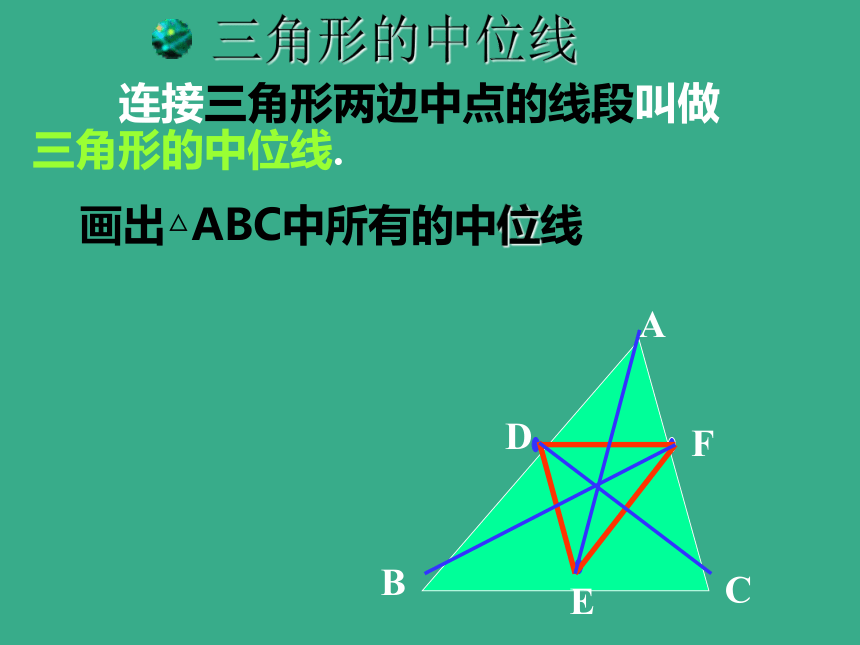
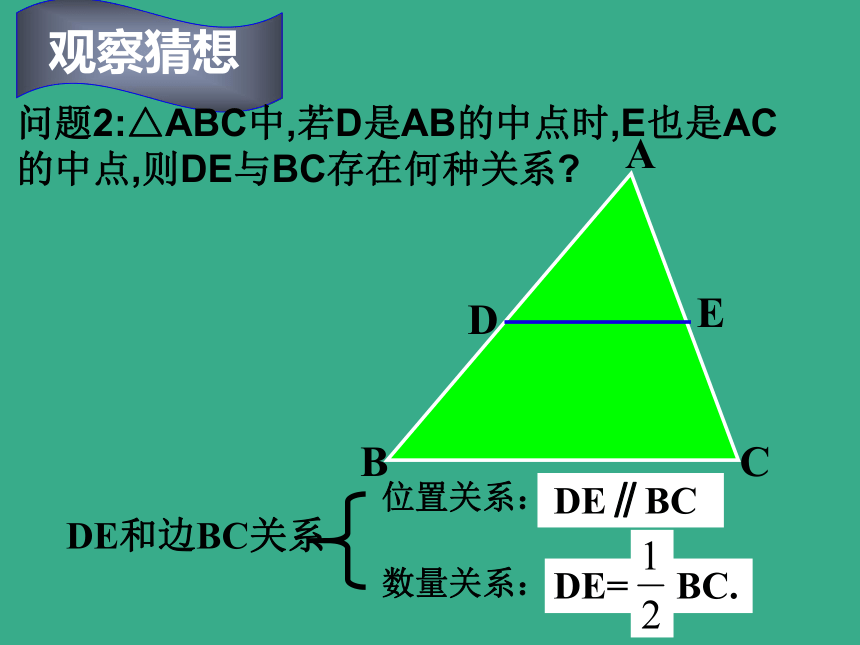
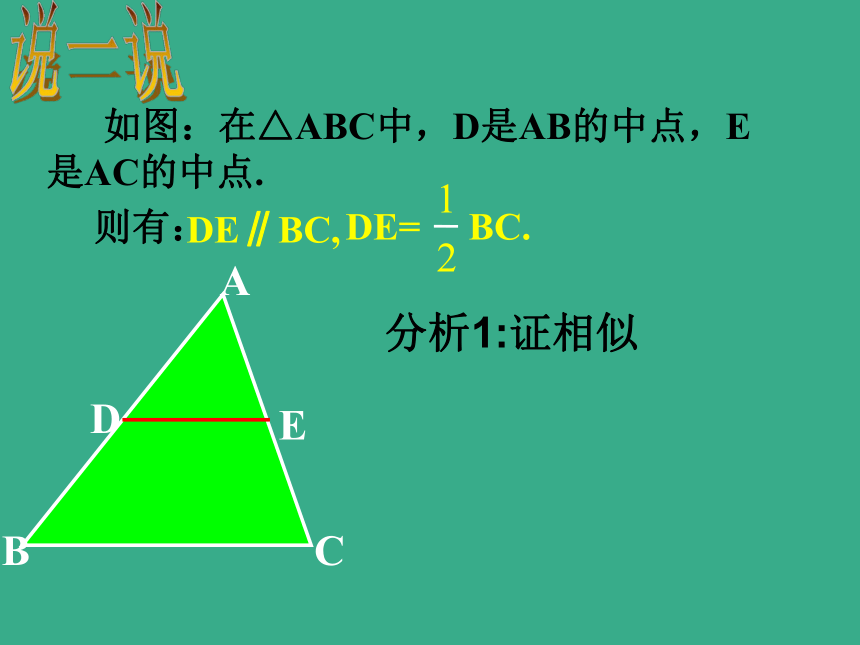
课件13张PPT。做一做24.4三角形中位线问题1:△ABC中,DE∥BC,则△ ADE 与△ ABC是什么关系?我们已经知道:若D是AB的中点时,E也是AC的中点三角形的中位线 连接三角形两边中点的线段叫做三角形的中位线.DEFDE和边BC关系数量关系：位置关系：DE= BC.问题2:△ABC中,若D是AB的中点时,E也是AC的中点,则DE与BC存在何种关系?
分析1:证相似
说一说分析2:
延长DE到F,使EF=DE , 连接CF
易证△ADE≌△CFE，
得CF=AD , CF//AB
又可得CF=BD,CF//BD
所以四边形BCFE是平行四边形
则有DE//BC,DE= DF= BC
三角形的中位线的性质 三角形的中位线平行于第三边，并且等于它的一半例1 求证三角形的一条中位线与第三边上
的中线互相平分.已知：△ABC中,AD=DB，BE=EC，AF=FC.
求证：AE与DF互相平分.证明:连接DE、EF例2证明:连接DE已知：△ABC中,CE、AD是它的中线，且相交于G.
求证：拓展取AC的中点F,假设BF与AD交于G′,
你能得出什么结论?所以G与G′重合三角形三条边上的中线交于一点,这个点成为三角形的
重心,重心与一边中点的连线的长是对应中线长的练习小结1.三角形的中位线定义.2.三角形的中位线定理.3.三角形的重心及其性质.