2022-2023学年重庆市南岸区珊瑚初级中学九年级(下)期中数学试卷(含解析)
文档属性
| 名称 | 2022-2023学年重庆市南岸区珊瑚初级中学九年级(下)期中数学试卷(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 598.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-03 11:34:04 | ||
图片预览




文档简介
2022-2023学年重庆市南岸区珊瑚初级中学九年级(下)期中数学试卷
第I卷(选择题)
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1. 下列各数中是有理数的是( )
A. B. C. D.
2. 如图图案中是中心对称图形,但不是轴对称图形的是( )
A. B. C. D.
3. 下列运算正确的是( )
A. B.
C. D.
4. 下列命题是真命题的是( )
A. 立方根等于它本身的数是,, B. 三角形的任意两边之和小于第三边
C. 采用抽样调查的方式检查飞机零部件 D. 五边形的内角和是
5. 如图,在外任取一点,连接、、,并分别取它们的中点、、,顺次连接、、得到,则下列说法错误的是( )
A. 与是位似图形 B. 与是相似图形
C. 与的周长比是: D. 与的面积比是:
6. 估算的结果最接近的整数是( )
A. B. C. D.
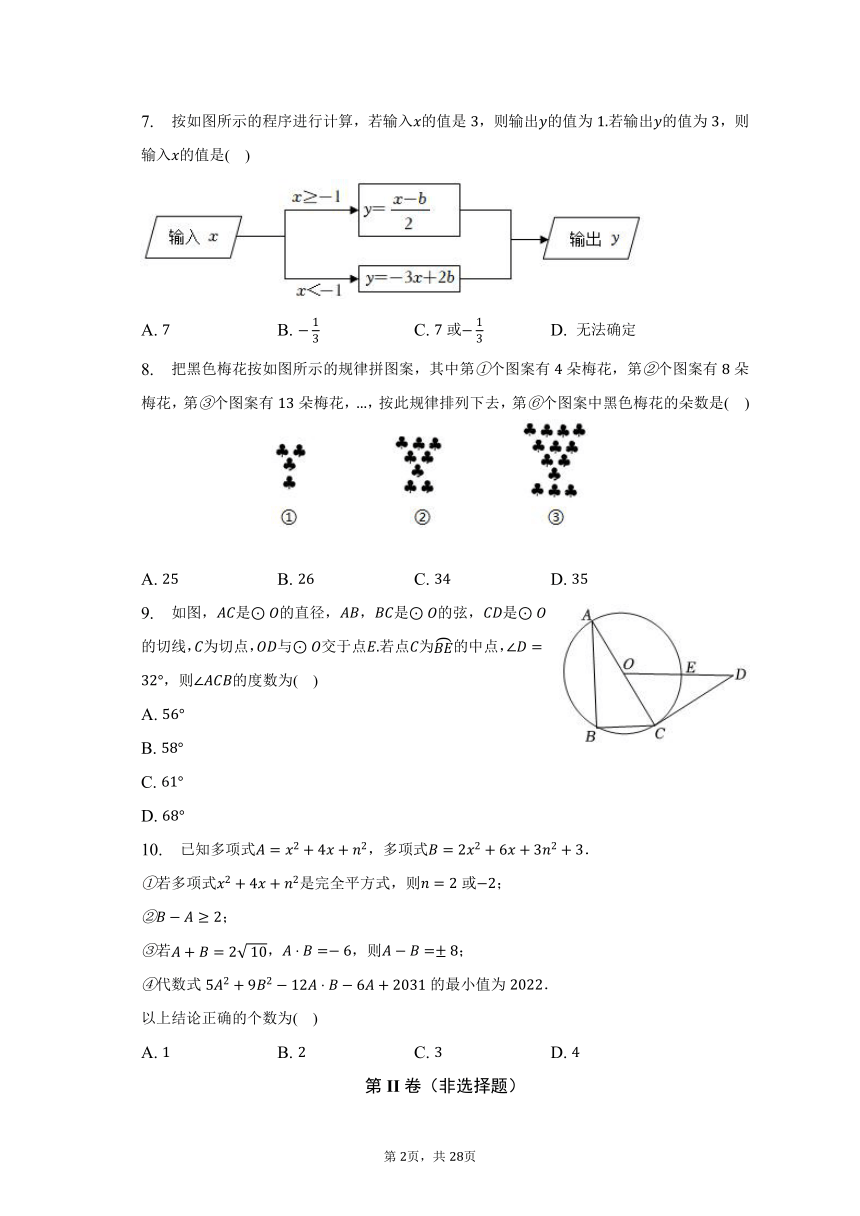
7. 按如图所示的程序进行计算,若输入的值是,则输出的值为若输出的值为,则输入的值是( )
A. B. C. 或 D. 无法确定
8. 把黑色梅花按如图所示的规律拼图案,其中第个图案有朵梅花,第个图案有朵梅花,第个图案有朵梅花,,按此规律排列下去,第个图案中黑色梅花的朵数是( )
A. B. C. D.
9. 如图,是的直径,,是的弦,是的切线,为切点,与交于点若点为的中点,,则的度数为( )
A.
B.
C.
D.
10. 已知多项式,多项式.
若多项式是完全平方式,则或;
;
若,,则;
代数式的最小值为.
以上结论正确的个数为( )
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共8小题,共32.0分)
11. 计算 ______ .
12. 人体最小的细胞是血小板,个血小板紧密排成一直线,数据用科学记数法表示是______ .
13. 函数的自变量的取值范围是______ .
14. 在一个不透明的口袋里装有除标号外完全一样的三个小球,小球上分别标有,,这三个数字,从袋中随机摸出一个小球,记标号为,然后放回摇匀后再随机摸出一个小球,记标号为,则满足的概率是______ .
15. 如图,在边长为的等边中,以为圆心、为半径画弧,再以为直径画半圆,则阴影部分的面积为______ .
16. 若整数的不等式组有解,且最多有个整数解,且使关于的分式方程的解为整数,则符合条件的所有整数的和为______ .
17. 如图,矩形中,,,点为的中点,点为上一点,连接、交于点,连接,当时,线段的长度是______ .
18. 若一个四位数正整数,其千位数字的倍与后三位组成的数的和得到的数称为的“笃学数”,记为,“笃学数”百位数字的倍与后两位组成的数的和得到的数称为的“图新数”,记为,例如:的“笃学数”为,的“图新数”,则 ______ ;若一个千位为,十位为的四位数的“笃学数”与“图新数”之和能被整除,则的最大值为______ .
三、解答题(本大题共8小题,共78.0分。解答应写出文字说明,证明过程或演算步骤)
19. 本小题分
化简:
;
.
20. 本小题分
在数学课上老师提出了如下问题:
如图,,当与满足什么关系时,?
小明认为时,他解答这个问题的思路和步骤如下,请根据小明的思路完成下面的作图与填空:
解:用直尺和圆规,在的右侧找一点,使只保留作图痕迹.
,
,
,
,
,
,
,
.
所以满足的关系为:当时,.
21. 本小题分
垃圾的分类回收不仅能够减少环境污染,美化家园,甚至能够变废为宝,节约能源,为增强学生垃圾分类意识,推动垃圾分类进校园,某中学组织全校学生参加了“垃圾分类知识竞赛”该校数学兴趣小组为了解全校学生竞赛分数情况,现从该校七年级、八年级中各随机抽攻了名学生的竞赛分数分及以上为“优秀”,分及以上为“及格”,学生竞赛分数记为分进行整理、描述和分析,下面给出了部分信息.
七年级名学生的竞赛成绩:,,,,,,,,,,,,,,,,,,,.
八年级名学生的竞赛成绩条形统计图如图::;:;:;:::组的数据为:,,,,,,,.
七、八年级抽取的学生的测试成绩的平均数、众数、中位数、优秀率如表所示:
年级 平均数 中位数 众数 优秀率
七年级
八年级
直接写出上述表中的,,的值;
根据以上数据,你认为该校七、八年级中哪个年级学生掌握垃圾分类知识较好?请说明理由写出一条理由即可;
该校七、八年级共名学生参加了此次测试活动,估计参加此次竞赛活动成绩优秀的学生人数是多少?
22. 本小题分
月日,重庆市长生桥垃圾镇埋场生态修复工程全面竣工验收,全国最大垃圾镇埋场摇身变为环境优美、空气宜人的生态绿地,实现了城市土地的循环再利用修复之初,一期工程共有吨垃圾要运走,计划由甲、乙两个工程队运走垃圾已知甲、乙两个工程队,原计划甲平均每天运走的垃圾比乙平均每天运走的垃圾多,这样甲运走吨垃圾的时间比乙运走剩下垃圾的时间少两天.
求原计划甲平均每天运垃圾多少吨?
实际施工时,甲平均每天运走的垃圾比原计划增加了吨,乙平均每天运走的垃圾比原计划增加了,甲、乙合作天后,甲临时有其他任务,剩下的垃圾由乙再单独工作天完成若运走每吨垃圾的运输费用为元,请求出甲工程队的运输费用.
23. 本小题分
如图,我国某海域里,渔船正在小岛的正西方向的处停留一艘渔政船在处巡逻,这时测得在处的渔船在它的北偏东方向上,渔政船的航行速度为每小时海里,它沿东北方向航行小时后到达处,测得渔船在它的西北方向.
求当渔政船到达处时,渔政船与渔船的距离;
若该渔政船在处测得小岛在它的北偏东方向上,这时渔船以每小时海里速度从处向小岛航行,同时渔政船以原速度也向小岛航行,则哪艘船先到达小岛参考数据:,,,,,
24. 本小题分
如图,在矩形中,,,动点,同时从点出发,点沿着方向运动,点沿着方向运动,有一点到达终点,另一点停止运动,已知点的速度是每秒个单位长度,点的速度是每秒个单位长度,若运动时间为秒,将的长度记为,的面积记为.
直接写出,与之间的函数表达式,并注明自变量的取值范围;
在平面直角坐标系中画出,的图象并写出的一条性质;
若函数与有两个交点,求的取值范围.
25. 本小题分
如图,在平面直角坐标系中,抛物线与直线交于点,.
求抛物线的函数解析式;
点是直线下方抛物线上一点,过点作轴的平行线,交于点,过点作的垂线,垂足为点,求周长的最大值及此时点的坐标;
在中取得最大值的条件下,将该抛物线沿水平方向向左平移个单位,点为点的对应点,点为原抛物线对称轴上一点在平移后抛物线上确定一点,使得以点,,,为顶点的四边形是平行四边形,写出所有符合条件的点的坐标,并写出求解点的坐标的其中一种情况的过程.
26. 本小题分
如图,在中,,,点在直线上运动,连接,以为斜边在直线的右侧作,其中,.
如图,点运动到点的左侧时,与相交于点,当平分时,若,求的长;
如图,点沿射线方向运动过程中,当时,连接,过点作交的延长线于点,取的中点,连接求证:;
如图,点沿射线方向运动过程中,连接,将线段绕点顺时针方向旋转,得到线段,连接、若,当取得最小值时,请直接写出的面积.
答案和解析
1.【答案】
【解析】解:、是无理数,不符合题意;
B、是有理数,符合题意;
C、是无理数,不符合题意;
D、是无理数,不符合题意.
故选:.
根据有理数和无理数的定义即可判断.
本题考查了实数的分类,有理数是有限小数或无限循环小数,无理数是无限不循环小数.
2.【答案】
【解析】解:、不是轴对称图形,不是中心对称图形,故此选项不符合题意;
B、是中心对称图形,但不是轴对称图形,故此选项符合题意;
C、是轴对称图形,也是中心对称图形,故此选项不符合题意;
D、既不是轴对称图形,也不是中心对称图形,故此选项不符合题意.
故选:.
根据轴对称图形与中心对称图形的概念求解.
此题主要考查了中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转度后两部分重合.
3.【答案】
【解析】解:根据合并同类项法则,,那么A错误,故A不符合题意.
B.根据完全平方公式,,那么B错误,故B不符合题意.
C.根据积的乘方与幂的乘方,,那么C正确,故C符合题意.
D.根据同底数幂的除法,,那么D错误,故D不符合题意.
故选:.
根据合并同类项法则、完全平方公式、积的乘方与幂的乘方法法则、同底数幂的除法法则解决此题.
本题主要考查合并同类项、完全平方公式、积的乘方与幂的乘方、同底数幂的除法,熟练掌握合并同类项法则、完全平方公式、积的乘方与幂的乘方、同底数幂的除法法则是解决本题的关键.
4.【答案】
【解析】解:、立方根等于它本身的数是,,,是真命题,符合题意;
B、三角形的任意两边之和大于第三边,故本选项说法是假命题,不符合题意;
C、采用全面调查的方式检查飞机零部件,故本选项说法是假命题,不符合题意;
D、五边形的内角和是,故本选项说法是假命题,不符合题意;
故选:.
根据立方根的概念、三角形的三边关系、抽样调查和全面调查、多边形的内角和定理判断即可.
本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
5.【答案】
【解析】解:、、的中点分别为、、,
,,,,,,
∽,
与是位似图形,位似中心为点,
与是相似图形,
与的周长比是:,与的面积比是:,
选项说法错误,
故选:.
根据三角形中位线定理得到,,,,,,进而证明∽,根据位似图形的概念、相似三角形的性质判断即可.
本题考查的是位似变换的概念和性质、相似三角形的性质、三角形中位线定理,掌握位似图形的概念、相似三角形的周长比等于相似比、面积比等于相似比的平方是解题的关键.
6.【答案】
【解析】解:
结果最接近的整数是.
故选:.
先化简计算,再作出估算.
本题考查了估算无理数的大小,关键是确定的近似值.
7.【答案】
【解析】解:输入的值是,且输出的值为,
,
解得,
当时,,
当时,,
若输出的值为,
设,则,
解得,
而,
此时输入的是;
设,则,
解得,
,
不符合题意,
综上所述,,
故选:.
根据输入的值是,则输出的值为求出的值,再分论讨论输出的值为时输入的值.
本题考查代数式的值,解题的关键是分类讨论思想的应用.
8.【答案】
【解析】解:第个图形有朵梅花,
第个图形有朵梅花,
第个图形有朵梅花,
第个图形中共有梅花的朵数是,
则第个图形中共有梅花的朵数是.
故选:.
观察图形变化,找到图形变化的规律,利用规律求解即可.
此题考查图形的变化规律,找出图形之间的运算规律,利用规律解决问题.
9.【答案】
【解析】解:是的切线,
,
,
,
,
点为的中点,
,
,
是的直径,
,
,
故选:.
根据切线的性质得到,根据直角三角形的性质求出,根据圆周角定理求出,计算即可.
本题考查的是切线的性质、圆周角定理以及弧、弦、圆心角之间的关系,掌握圆的切线垂直于过切点的半径是解题的关键.
10.【答案】
【解析】解:根据题意得,
,
解得或,
故正确;
,
,,
,
,
故正确;
,,
,
由可知,,
,
故错误;
,
又,,
,
最小值为,
故错误.
故选:.
利用完全平方公式的形式求解;
利用整式的加减运算和配方法求解;
利用完全平方和和完全平方差公式求解;
利用完全平方公式和配方法求解.
本题主要考查了完全平方公式和配方法的应用,同时也利用非负数的性质求最值,题目比较难.
11.【答案】
【解析】解:原式
.
故答案为:.
直接利用零指数幂的性质化简,进而得出答案.
此题主要考查了实数的运算,正确化简各数是解题关键.
12.【答案】
【解析】解:.
故答案为:.
科学记数法的表示形式为的形式,其中,为整数.确定的值时,要看把原数变成时,小数点移动了多少位,的绝对值与小数点移动的位数相同.当原数绝对值时,是正整数;当原数的绝对值时,是负整数.
此题考查科学记数法的表示方法.科学记数法的表示形式为的形式,其中,为整数,表示时关键要正确确定的值以及的值.
13.【答案】且
【解析】解:由题可得,,
解得:且.
故答案为:且.
当表达式的分母中含有自变量时,自变量取值要使分母不为零.当函数的表达式是偶次根式时,自变量的取值范围必须使被开方数不小于零.据此可得自变量的取值范围.
本题主要考查了函数自变量的取值范围,自变量的取值范围必须使含有自变量的表达式都有意义.
14.【答案】
【解析】解:画树状图如下:
共有种等可能的结果,满足的结果有种,
满足的概率为,
故答案为:.
画树状图,共有种等可能的结果,满足的结果有种,再由概率公式求解即可.
此题考查的是用树状图法求概率.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件.用到的知识点为:概率所求情况数与总情况数之比.
15.【答案】
【解析】解:设以为直径画半圆交、于点、,
等边中,且以为直径画半圆,
,,
,,,都是等边三角形,
.
故答案为:.
根据阴影部分的面积,利用扇形的面积公式以及三角形的面积公式求解即可.
本题考查了扇形的面积计算,解答本题的关键是仔细观察图形,利用差值法求不规则图形的面积.
16.【答案】
【解析】解:解不等式组得:,
不等式组有解,且最多有个整数解,
,
解得:,
分式方程,
去分母得:,
解得:,
分式方程的解为整数,
为整数,且,
符合条件的所有整数的值为,,,
符合条件的所有整数的和为.
故答案为:.
解不等式组,根据题意确定的范围,再解出分式方程,根据题意确定的范围,再根据题意计算即可.
本题考查的是分式方程的解法、一元一次不等式组的解法,掌握解分式方程、一元一次不等式组的一般步骤是解题的关键.
17.【答案】
【解析】解:在矩形中,,,点为的中点,
,,,
,,
,
,
,
,
,
∽,
,
,
,
,
,,
∽,
,
,
,
故答案为:.
根据矩形的性质得到,,,根据勾股定理得到,根据相似三角形的判定和性质定理即可得到结论.
本题考查了矩形的性质,相似三角形的判定和性质,勾股定理,熟练掌握相似三角形的判定和性质定理是解题的关键.
18.【答案】
【解析】解:,
;
设四位数的百位数字为,个位数字为为整数,
则,
,即,
,
,
能被整除,且,,,为整数,
当时,即能被整除,值无解;
当时,即能被整除,值无解;
当时,即能被整除,值无解;
当时,即能被整除,值无解;
当时,即能被整除,符合题意;
当时,即能被整除,符合题意;
当时,即能被整除,符合题意;
当时,即能被整除,值无解;
当时,即能被整除,值无解;
当时,即能被整除,值无解.
综上,符合条件的四位数有:,,,其中的最大值为.
故答案为:,.
根据“笃学数”“图新数”的定义即可求得;设四位数的百位数字为,个位数字为为整数,根据“笃学数”“图新数”的定义可求得,,则,再根据“笃学数”与“图新数”之和能被整除,分类讨论即可.
本题主要考查新定义运算、整式的加减、数的整除,解题关键在于理解“笃学数”“图新数”的定义.
19.【答案】解:原式
;
原式
.
【解析】先展开.去括号,再合并同类项即可;
先通分算括号内的,把除化为乘,再约分即可.
本题考查整式运算及分式的运算,解题的根据是掌握整式运算、分式运算的相关法则及运算顺序.
20.【答案】
【解析】解:图形如图所示:
,
,
,
,
,
,
,
.
所以满足的关系为:当时,.
故答案为:,,,.
根据要求作出图形,利用平行线的判定和性质证明即可.
本题考查作图复杂作图,平行线的判定和性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
21.【答案】解:八年级学生成绩的中位数为:,
七年级名学生成绩的出现次数最多的是分,出现次,因此众数,
八年级优秀的人数是,所以优秀率,
答:,,;
七年级学生掌握垃圾分类知识较好,
理由:虽然两个年级的平均分相等,但七年级的众数、中位数和优秀率均高于八年级,
七年级学生掌握垃圾分类知识较好;
人,
答:参加此次竞赛活动成绩优秀的学生人数是人.
【解析】根据中位数、众数的意义,分别计算即可;
根据表格中的数据可得结论;
根据两个年级参加活动的人数和优秀率可得答案.
本题考查中位数、众数、平均数的意义和计算方法,理解各个概念的内涵和计算方法,是解题的关键.
22.【答案】解:设原计划乙平均每天运垃圾吨,则甲平均每天运垃圾吨,
根据题意得:,
解得:,
经检验,是原方程的解,且符合题意,
,
答:原计划甲平均每天运走垃圾吨;
根据题意得:,
解得:,
甲工程队运输费用为:元,
答:甲工程队的运输费用为元.
【解析】设原计划乙平均每天运垃圾吨,则甲平均每天运垃圾吨,由题意:甲运走吨垃圾的时间比乙运走剩下垃圾的时间少两天.即可列出关于的分式方程,解分式方程,即可解决问题;
由题意:甲、乙合作天后,甲临时有其他任务,剩下的垃圾由乙再单独工作天完成.即可列出关于的一元一次方程,解方程,即可得出结论.
本题考查了分式方程的应用以及一元一次方程的应用,解题的关键是:找准等量关系,正确列出分式方程;找准等量关系,正确列出一元一次方程.
23.【答案】解:由题意知,,,,,海里,
,,
在中,
海里,
答:渔政船与渔船的距离为海里.
过点作的垂线,垂足为点,
,
由题意知,
在中,,
海里,
海里,
在中,,
,
海里,
渔船的到达小岛的时间:小时或者,
渔政船到达小岛的时间:小时或者,
,
,
即渔政船先到达小岛.
【解析】,,在中,运用正切函数即可得;
过点作的垂线,垂足为点,可得,由题意知,在中,,运用三角函数得,,在中,,运用三角函数得,,即可得渔船的到达小岛的时间:小时,渔政船到达小岛的时间:,可得,即可得.
本题考查了解直角三角形的应用,解题的关键是理解题意,掌握锐角三角函数,添加辅助线构造直角三角形.
24.【答案】解:当时,点在上运动,
则,
当时,点在上运动,
同理可得:,
即,
则;
对于,
当时,,当时,,当时,,
对于,
当时,,当时,,
通过对上述点描点、连线、绘制图象如下:
从图象看,当时,随的增大而减小,当,随的增大而增大答案不唯一;
从图象看,当函数过点和时,两条直线恰好有个交点,
将代入得:,则,
将代入得:,则,
的取值范围为:.
【解析】当时,点在上运动,则,当时,点在上运动,同理可解;由,即可求解;
通过取点、描点、连线、绘制图象即可求解;
从图象看,当函数过点和时,两条直线恰好有个交点,进而求解.
本题考查了一次函数综合运用,涉及到矩形性质,一次函数的基本性质,主要考查学生分析问题和解决问题的能力,题目比较典型,但是有一定的难度.
25.【答案】解:分别把点,,
代入得:,
解得:,
所以抛物线的解析式为;
,
,,,
直线的解析式为:,
设:,,
,
当时,最大为,
轴,,
,,
∽,
,
,
所以当最大为时,的周长最大为,
此时;
,将该抛物线沿水平方向向左平移个单位,
则平移后的解析式为,,
设,,,
当为对角线时,由平行四边形对角线中点坐标相同可得:,
可得,则,即:;
当为对角线时,由平行四边形对角线中点坐标相同可得:,
可得,则,即:;
当为对角线时,由平行四边形对角线中点坐标相同可得:,
可得,则,即:;
综上,符合条件的点的坐标为:,,.
【解析】利用待定系数法求解即可;
先求得直线的解析式为:,设,,可得,当时,最大为,再证∽,可得,进而可知,可知当最大为时,的周长最大为,得此时的坐标为;
先求出平移后的抛物线解析式为,,设,,,然后分当为对角线时,当为对角线时,当为对角线时,三种情况利用平行四边形对角线中点坐标相同列出方程求解即可.
本题主要考查了二次函数综合,一次函数与几何综合,二次函数图象的平移,平行四边形的性质,待定系数法求二次函数解析式等等,利用分类讨论的思想求解是解题的关键.
26.【答案】解:如图中,过点作于,
在中,,,
,,
是的角平分线,,
,
,
,
,
.
证明:如图中,取的中点,连接,,.
,
,
,
,
,
,
,
,
≌,
,,
在和中,,,
点为的中点,
,,,
为的中点,
,
,
,
,
,且,
≌,
,
,
是底角为的等腰三角形,
,
.
解:如图中,当点在射线上时,点在射线上运动,此时,
则线段绕点顺时针旋转得到线段,则点在上运动,在点的左侧作射线,使得,过点作于,
当点,,三点共线时,最短,此时点也在线段上,则,,
,
,
过点作于,则,
.
【解析】如图中,过点作于,证明是等腰直角三角形即可解决问题.
如图中,取的中点,连接,,证明是底角为的等腰三角形,即可解决问题.
如图中,当点在射线上时,点在射线上运动,此时,当点,,三点共线时,最短,此时点也在线段上,由此即可解决问题.
本题属于几何变换综合题,考查了等腰直角三角形的判定和性质,全等三角形的判定和性质,解直角三角形,垂线段最短,直角三角形斜边中线的性质等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,学会利用垂线段最短解决最值问题,属于中考压轴题.
第1页,共1页
第I卷(选择题)
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1. 下列各数中是有理数的是( )
A. B. C. D.
2. 如图图案中是中心对称图形,但不是轴对称图形的是( )
A. B. C. D.
3. 下列运算正确的是( )
A. B.
C. D.
4. 下列命题是真命题的是( )
A. 立方根等于它本身的数是,, B. 三角形的任意两边之和小于第三边
C. 采用抽样调查的方式检查飞机零部件 D. 五边形的内角和是
5. 如图,在外任取一点,连接、、,并分别取它们的中点、、,顺次连接、、得到,则下列说法错误的是( )
A. 与是位似图形 B. 与是相似图形
C. 与的周长比是: D. 与的面积比是:
6. 估算的结果最接近的整数是( )
A. B. C. D.
7. 按如图所示的程序进行计算,若输入的值是,则输出的值为若输出的值为,则输入的值是( )
A. B. C. 或 D. 无法确定
8. 把黑色梅花按如图所示的规律拼图案,其中第个图案有朵梅花,第个图案有朵梅花,第个图案有朵梅花,,按此规律排列下去,第个图案中黑色梅花的朵数是( )
A. B. C. D.
9. 如图,是的直径,,是的弦,是的切线,为切点,与交于点若点为的中点,,则的度数为( )
A.
B.
C.
D.
10. 已知多项式,多项式.
若多项式是完全平方式,则或;
;
若,,则;
代数式的最小值为.
以上结论正确的个数为( )
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共8小题,共32.0分)
11. 计算 ______ .
12. 人体最小的细胞是血小板,个血小板紧密排成一直线,数据用科学记数法表示是______ .
13. 函数的自变量的取值范围是______ .
14. 在一个不透明的口袋里装有除标号外完全一样的三个小球,小球上分别标有,,这三个数字,从袋中随机摸出一个小球,记标号为,然后放回摇匀后再随机摸出一个小球,记标号为,则满足的概率是______ .
15. 如图,在边长为的等边中,以为圆心、为半径画弧,再以为直径画半圆,则阴影部分的面积为______ .
16. 若整数的不等式组有解,且最多有个整数解,且使关于的分式方程的解为整数,则符合条件的所有整数的和为______ .
17. 如图,矩形中,,,点为的中点,点为上一点,连接、交于点,连接,当时,线段的长度是______ .
18. 若一个四位数正整数,其千位数字的倍与后三位组成的数的和得到的数称为的“笃学数”,记为,“笃学数”百位数字的倍与后两位组成的数的和得到的数称为的“图新数”,记为,例如:的“笃学数”为,的“图新数”,则 ______ ;若一个千位为,十位为的四位数的“笃学数”与“图新数”之和能被整除,则的最大值为______ .
三、解答题(本大题共8小题,共78.0分。解答应写出文字说明,证明过程或演算步骤)
19. 本小题分
化简:
;
.
20. 本小题分
在数学课上老师提出了如下问题:
如图,,当与满足什么关系时,?
小明认为时,他解答这个问题的思路和步骤如下,请根据小明的思路完成下面的作图与填空:
解:用直尺和圆规,在的右侧找一点,使只保留作图痕迹.
,
,
,
,
,
,
,
.
所以满足的关系为:当时,.
21. 本小题分
垃圾的分类回收不仅能够减少环境污染,美化家园,甚至能够变废为宝,节约能源,为增强学生垃圾分类意识,推动垃圾分类进校园,某中学组织全校学生参加了“垃圾分类知识竞赛”该校数学兴趣小组为了解全校学生竞赛分数情况,现从该校七年级、八年级中各随机抽攻了名学生的竞赛分数分及以上为“优秀”,分及以上为“及格”,学生竞赛分数记为分进行整理、描述和分析,下面给出了部分信息.
七年级名学生的竞赛成绩:,,,,,,,,,,,,,,,,,,,.
八年级名学生的竞赛成绩条形统计图如图::;:;:;:::组的数据为:,,,,,,,.
七、八年级抽取的学生的测试成绩的平均数、众数、中位数、优秀率如表所示:
年级 平均数 中位数 众数 优秀率
七年级
八年级
直接写出上述表中的,,的值;
根据以上数据,你认为该校七、八年级中哪个年级学生掌握垃圾分类知识较好?请说明理由写出一条理由即可;
该校七、八年级共名学生参加了此次测试活动,估计参加此次竞赛活动成绩优秀的学生人数是多少?
22. 本小题分
月日,重庆市长生桥垃圾镇埋场生态修复工程全面竣工验收,全国最大垃圾镇埋场摇身变为环境优美、空气宜人的生态绿地,实现了城市土地的循环再利用修复之初,一期工程共有吨垃圾要运走,计划由甲、乙两个工程队运走垃圾已知甲、乙两个工程队,原计划甲平均每天运走的垃圾比乙平均每天运走的垃圾多,这样甲运走吨垃圾的时间比乙运走剩下垃圾的时间少两天.
求原计划甲平均每天运垃圾多少吨?
实际施工时,甲平均每天运走的垃圾比原计划增加了吨,乙平均每天运走的垃圾比原计划增加了,甲、乙合作天后,甲临时有其他任务,剩下的垃圾由乙再单独工作天完成若运走每吨垃圾的运输费用为元,请求出甲工程队的运输费用.
23. 本小题分
如图,我国某海域里,渔船正在小岛的正西方向的处停留一艘渔政船在处巡逻,这时测得在处的渔船在它的北偏东方向上,渔政船的航行速度为每小时海里,它沿东北方向航行小时后到达处,测得渔船在它的西北方向.
求当渔政船到达处时,渔政船与渔船的距离;
若该渔政船在处测得小岛在它的北偏东方向上,这时渔船以每小时海里速度从处向小岛航行,同时渔政船以原速度也向小岛航行,则哪艘船先到达小岛参考数据:,,,,,
24. 本小题分
如图,在矩形中,,,动点,同时从点出发,点沿着方向运动,点沿着方向运动,有一点到达终点,另一点停止运动,已知点的速度是每秒个单位长度,点的速度是每秒个单位长度,若运动时间为秒,将的长度记为,的面积记为.
直接写出,与之间的函数表达式,并注明自变量的取值范围;
在平面直角坐标系中画出,的图象并写出的一条性质;
若函数与有两个交点,求的取值范围.
25. 本小题分
如图,在平面直角坐标系中,抛物线与直线交于点,.
求抛物线的函数解析式;
点是直线下方抛物线上一点,过点作轴的平行线,交于点,过点作的垂线,垂足为点,求周长的最大值及此时点的坐标;
在中取得最大值的条件下,将该抛物线沿水平方向向左平移个单位,点为点的对应点,点为原抛物线对称轴上一点在平移后抛物线上确定一点,使得以点,,,为顶点的四边形是平行四边形,写出所有符合条件的点的坐标,并写出求解点的坐标的其中一种情况的过程.
26. 本小题分
如图,在中,,,点在直线上运动,连接,以为斜边在直线的右侧作,其中,.
如图,点运动到点的左侧时,与相交于点,当平分时,若,求的长;
如图,点沿射线方向运动过程中,当时,连接,过点作交的延长线于点,取的中点,连接求证:;
如图,点沿射线方向运动过程中,连接,将线段绕点顺时针方向旋转,得到线段,连接、若,当取得最小值时,请直接写出的面积.
答案和解析
1.【答案】
【解析】解:、是无理数,不符合题意;
B、是有理数,符合题意;
C、是无理数,不符合题意;
D、是无理数,不符合题意.
故选:.
根据有理数和无理数的定义即可判断.
本题考查了实数的分类,有理数是有限小数或无限循环小数,无理数是无限不循环小数.
2.【答案】
【解析】解:、不是轴对称图形,不是中心对称图形,故此选项不符合题意;
B、是中心对称图形,但不是轴对称图形,故此选项符合题意;
C、是轴对称图形,也是中心对称图形,故此选项不符合题意;
D、既不是轴对称图形,也不是中心对称图形,故此选项不符合题意.
故选:.
根据轴对称图形与中心对称图形的概念求解.
此题主要考查了中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转度后两部分重合.
3.【答案】
【解析】解:根据合并同类项法则,,那么A错误,故A不符合题意.
B.根据完全平方公式,,那么B错误,故B不符合题意.
C.根据积的乘方与幂的乘方,,那么C正确,故C符合题意.
D.根据同底数幂的除法,,那么D错误,故D不符合题意.
故选:.
根据合并同类项法则、完全平方公式、积的乘方与幂的乘方法法则、同底数幂的除法法则解决此题.
本题主要考查合并同类项、完全平方公式、积的乘方与幂的乘方、同底数幂的除法,熟练掌握合并同类项法则、完全平方公式、积的乘方与幂的乘方、同底数幂的除法法则是解决本题的关键.
4.【答案】
【解析】解:、立方根等于它本身的数是,,,是真命题,符合题意;
B、三角形的任意两边之和大于第三边,故本选项说法是假命题,不符合题意;
C、采用全面调查的方式检查飞机零部件,故本选项说法是假命题,不符合题意;
D、五边形的内角和是,故本选项说法是假命题,不符合题意;
故选:.
根据立方根的概念、三角形的三边关系、抽样调查和全面调查、多边形的内角和定理判断即可.
本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
5.【答案】
【解析】解:、、的中点分别为、、,
,,,,,,
∽,
与是位似图形,位似中心为点,
与是相似图形,
与的周长比是:,与的面积比是:,
选项说法错误,
故选:.
根据三角形中位线定理得到,,,,,,进而证明∽,根据位似图形的概念、相似三角形的性质判断即可.
本题考查的是位似变换的概念和性质、相似三角形的性质、三角形中位线定理,掌握位似图形的概念、相似三角形的周长比等于相似比、面积比等于相似比的平方是解题的关键.
6.【答案】
【解析】解:
结果最接近的整数是.
故选:.
先化简计算,再作出估算.
本题考查了估算无理数的大小,关键是确定的近似值.
7.【答案】
【解析】解:输入的值是,且输出的值为,
,
解得,
当时,,
当时,,
若输出的值为,
设,则,
解得,
而,
此时输入的是;
设,则,
解得,
,
不符合题意,
综上所述,,
故选:.
根据输入的值是,则输出的值为求出的值,再分论讨论输出的值为时输入的值.
本题考查代数式的值,解题的关键是分类讨论思想的应用.
8.【答案】
【解析】解:第个图形有朵梅花,
第个图形有朵梅花,
第个图形有朵梅花,
第个图形中共有梅花的朵数是,
则第个图形中共有梅花的朵数是.
故选:.
观察图形变化,找到图形变化的规律,利用规律求解即可.
此题考查图形的变化规律,找出图形之间的运算规律,利用规律解决问题.
9.【答案】
【解析】解:是的切线,
,
,
,
,
点为的中点,
,
,
是的直径,
,
,
故选:.
根据切线的性质得到,根据直角三角形的性质求出,根据圆周角定理求出,计算即可.
本题考查的是切线的性质、圆周角定理以及弧、弦、圆心角之间的关系,掌握圆的切线垂直于过切点的半径是解题的关键.
10.【答案】
【解析】解:根据题意得,
,
解得或,
故正确;
,
,,
,
,
故正确;
,,
,
由可知,,
,
故错误;
,
又,,
,
最小值为,
故错误.
故选:.
利用完全平方公式的形式求解;
利用整式的加减运算和配方法求解;
利用完全平方和和完全平方差公式求解;
利用完全平方公式和配方法求解.
本题主要考查了完全平方公式和配方法的应用,同时也利用非负数的性质求最值,题目比较难.
11.【答案】
【解析】解:原式
.
故答案为:.
直接利用零指数幂的性质化简,进而得出答案.
此题主要考查了实数的运算,正确化简各数是解题关键.
12.【答案】
【解析】解:.
故答案为:.
科学记数法的表示形式为的形式,其中,为整数.确定的值时,要看把原数变成时,小数点移动了多少位,的绝对值与小数点移动的位数相同.当原数绝对值时,是正整数;当原数的绝对值时,是负整数.
此题考查科学记数法的表示方法.科学记数法的表示形式为的形式,其中,为整数,表示时关键要正确确定的值以及的值.
13.【答案】且
【解析】解:由题可得,,
解得:且.
故答案为:且.
当表达式的分母中含有自变量时,自变量取值要使分母不为零.当函数的表达式是偶次根式时,自变量的取值范围必须使被开方数不小于零.据此可得自变量的取值范围.
本题主要考查了函数自变量的取值范围,自变量的取值范围必须使含有自变量的表达式都有意义.
14.【答案】
【解析】解:画树状图如下:
共有种等可能的结果,满足的结果有种,
满足的概率为,
故答案为:.
画树状图,共有种等可能的结果,满足的结果有种,再由概率公式求解即可.
此题考查的是用树状图法求概率.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件.用到的知识点为:概率所求情况数与总情况数之比.
15.【答案】
【解析】解:设以为直径画半圆交、于点、,
等边中,且以为直径画半圆,
,,
,,,都是等边三角形,
.
故答案为:.
根据阴影部分的面积,利用扇形的面积公式以及三角形的面积公式求解即可.
本题考查了扇形的面积计算,解答本题的关键是仔细观察图形,利用差值法求不规则图形的面积.
16.【答案】
【解析】解:解不等式组得:,
不等式组有解,且最多有个整数解,
,
解得:,
分式方程,
去分母得:,
解得:,
分式方程的解为整数,
为整数,且,
符合条件的所有整数的值为,,,
符合条件的所有整数的和为.
故答案为:.
解不等式组,根据题意确定的范围,再解出分式方程,根据题意确定的范围,再根据题意计算即可.
本题考查的是分式方程的解法、一元一次不等式组的解法,掌握解分式方程、一元一次不等式组的一般步骤是解题的关键.
17.【答案】
【解析】解:在矩形中,,,点为的中点,
,,,
,,
,
,
,
,
,
∽,
,
,
,
,
,,
∽,
,
,
,
故答案为:.
根据矩形的性质得到,,,根据勾股定理得到,根据相似三角形的判定和性质定理即可得到结论.
本题考查了矩形的性质,相似三角形的判定和性质,勾股定理,熟练掌握相似三角形的判定和性质定理是解题的关键.
18.【答案】
【解析】解:,
;
设四位数的百位数字为,个位数字为为整数,
则,
,即,
,
,
能被整除,且,,,为整数,
当时,即能被整除,值无解;
当时,即能被整除,值无解;
当时,即能被整除,值无解;
当时,即能被整除,值无解;
当时,即能被整除,符合题意;
当时,即能被整除,符合题意;
当时,即能被整除,符合题意;
当时,即能被整除,值无解;
当时,即能被整除,值无解;
当时,即能被整除,值无解.
综上,符合条件的四位数有:,,,其中的最大值为.
故答案为:,.
根据“笃学数”“图新数”的定义即可求得;设四位数的百位数字为,个位数字为为整数,根据“笃学数”“图新数”的定义可求得,,则,再根据“笃学数”与“图新数”之和能被整除,分类讨论即可.
本题主要考查新定义运算、整式的加减、数的整除,解题关键在于理解“笃学数”“图新数”的定义.
19.【答案】解:原式
;
原式
.
【解析】先展开.去括号,再合并同类项即可;
先通分算括号内的,把除化为乘,再约分即可.
本题考查整式运算及分式的运算,解题的根据是掌握整式运算、分式运算的相关法则及运算顺序.
20.【答案】
【解析】解:图形如图所示:
,
,
,
,
,
,
,
.
所以满足的关系为:当时,.
故答案为:,,,.
根据要求作出图形,利用平行线的判定和性质证明即可.
本题考查作图复杂作图,平行线的判定和性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
21.【答案】解:八年级学生成绩的中位数为:,
七年级名学生成绩的出现次数最多的是分,出现次,因此众数,
八年级优秀的人数是,所以优秀率,
答:,,;
七年级学生掌握垃圾分类知识较好,
理由:虽然两个年级的平均分相等,但七年级的众数、中位数和优秀率均高于八年级,
七年级学生掌握垃圾分类知识较好;
人,
答:参加此次竞赛活动成绩优秀的学生人数是人.
【解析】根据中位数、众数的意义,分别计算即可;
根据表格中的数据可得结论;
根据两个年级参加活动的人数和优秀率可得答案.
本题考查中位数、众数、平均数的意义和计算方法,理解各个概念的内涵和计算方法,是解题的关键.
22.【答案】解:设原计划乙平均每天运垃圾吨,则甲平均每天运垃圾吨,
根据题意得:,
解得:,
经检验,是原方程的解,且符合题意,
,
答:原计划甲平均每天运走垃圾吨;
根据题意得:,
解得:,
甲工程队运输费用为:元,
答:甲工程队的运输费用为元.
【解析】设原计划乙平均每天运垃圾吨,则甲平均每天运垃圾吨,由题意:甲运走吨垃圾的时间比乙运走剩下垃圾的时间少两天.即可列出关于的分式方程,解分式方程,即可解决问题;
由题意:甲、乙合作天后,甲临时有其他任务,剩下的垃圾由乙再单独工作天完成.即可列出关于的一元一次方程,解方程,即可得出结论.
本题考查了分式方程的应用以及一元一次方程的应用,解题的关键是:找准等量关系,正确列出分式方程;找准等量关系,正确列出一元一次方程.
23.【答案】解:由题意知,,,,,海里,
,,
在中,
海里,
答:渔政船与渔船的距离为海里.
过点作的垂线,垂足为点,
,
由题意知,
在中,,
海里,
海里,
在中,,
,
海里,
渔船的到达小岛的时间:小时或者,
渔政船到达小岛的时间:小时或者,
,
,
即渔政船先到达小岛.
【解析】,,在中,运用正切函数即可得;
过点作的垂线,垂足为点,可得,由题意知,在中,,运用三角函数得,,在中,,运用三角函数得,,即可得渔船的到达小岛的时间:小时,渔政船到达小岛的时间:,可得,即可得.
本题考查了解直角三角形的应用,解题的关键是理解题意,掌握锐角三角函数,添加辅助线构造直角三角形.
24.【答案】解:当时,点在上运动,
则,
当时,点在上运动,
同理可得:,
即,
则;
对于,
当时,,当时,,当时,,
对于,
当时,,当时,,
通过对上述点描点、连线、绘制图象如下:
从图象看,当时,随的增大而减小,当,随的增大而增大答案不唯一;
从图象看,当函数过点和时,两条直线恰好有个交点,
将代入得:,则,
将代入得:,则,
的取值范围为:.
【解析】当时,点在上运动,则,当时,点在上运动,同理可解;由,即可求解;
通过取点、描点、连线、绘制图象即可求解;
从图象看,当函数过点和时,两条直线恰好有个交点,进而求解.
本题考查了一次函数综合运用,涉及到矩形性质,一次函数的基本性质,主要考查学生分析问题和解决问题的能力,题目比较典型,但是有一定的难度.
25.【答案】解:分别把点,,
代入得:,
解得:,
所以抛物线的解析式为;
,
,,,
直线的解析式为:,
设:,,
,
当时,最大为,
轴,,
,,
∽,
,
,
所以当最大为时,的周长最大为,
此时;
,将该抛物线沿水平方向向左平移个单位,
则平移后的解析式为,,
设,,,
当为对角线时,由平行四边形对角线中点坐标相同可得:,
可得,则,即:;
当为对角线时,由平行四边形对角线中点坐标相同可得:,
可得,则,即:;
当为对角线时,由平行四边形对角线中点坐标相同可得:,
可得,则,即:;
综上,符合条件的点的坐标为:,,.
【解析】利用待定系数法求解即可;
先求得直线的解析式为:,设,,可得,当时,最大为,再证∽,可得,进而可知,可知当最大为时,的周长最大为,得此时的坐标为;
先求出平移后的抛物线解析式为,,设,,,然后分当为对角线时,当为对角线时,当为对角线时,三种情况利用平行四边形对角线中点坐标相同列出方程求解即可.
本题主要考查了二次函数综合,一次函数与几何综合,二次函数图象的平移,平行四边形的性质,待定系数法求二次函数解析式等等,利用分类讨论的思想求解是解题的关键.
26.【答案】解:如图中,过点作于,
在中,,,
,,
是的角平分线,,
,
,
,
,
.
证明:如图中,取的中点,连接,,.
,
,
,
,
,
,
,
,
≌,
,,
在和中,,,
点为的中点,
,,,
为的中点,
,
,
,
,
,且,
≌,
,
,
是底角为的等腰三角形,
,
.
解:如图中,当点在射线上时,点在射线上运动,此时,
则线段绕点顺时针旋转得到线段,则点在上运动,在点的左侧作射线,使得,过点作于,
当点,,三点共线时,最短,此时点也在线段上,则,,
,
,
过点作于,则,
.
【解析】如图中,过点作于,证明是等腰直角三角形即可解决问题.
如图中,取的中点,连接,,证明是底角为的等腰三角形,即可解决问题.
如图中,当点在射线上时,点在射线上运动,此时,当点,,三点共线时,最短,此时点也在线段上,由此即可解决问题.
本题属于几何变换综合题,考查了等腰直角三角形的判定和性质,全等三角形的判定和性质,解直角三角形,垂线段最短,直角三角形斜边中线的性质等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,学会利用垂线段最短解决最值问题,属于中考压轴题.
第1页,共1页
同课章节目录
