3.2.1双曲线的定义及基本方程 课件(共28张PPT)
文档属性
| 名称 | 3.2.1双曲线的定义及基本方程 课件(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 17.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-02 14:45:06 | ||
图片预览







文档简介
(共28张PPT)
3.2.1双曲线
及其标准方程
04
02
回顾旧知
01
巩固练习
03
新知导入
课堂小结
目 录
作业布置
05
01
回顾旧知
椭圆的定义是什么?
平面内与两个定点F1、F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆。
椭圆的基本方程是什么?
|MF1|+|MF2|=2a( 2a>2c>0) ,
点M的轨迹是椭圆;
若2a=2c ,
点M的轨迹是线段F1F2;
若2a<2c ,
点M的轨迹不存在。
三角形的两边之和大于第三边;两边之差小于第三边
02
新知导入
平面内与两个定点F1、F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆。
平面内与两个定点F1、F2的距离的差为非零常数的点的轨迹叫什么呢?
02
新知导入
小组实验探究:
材料:拉链,木板,纸,笔,图钉
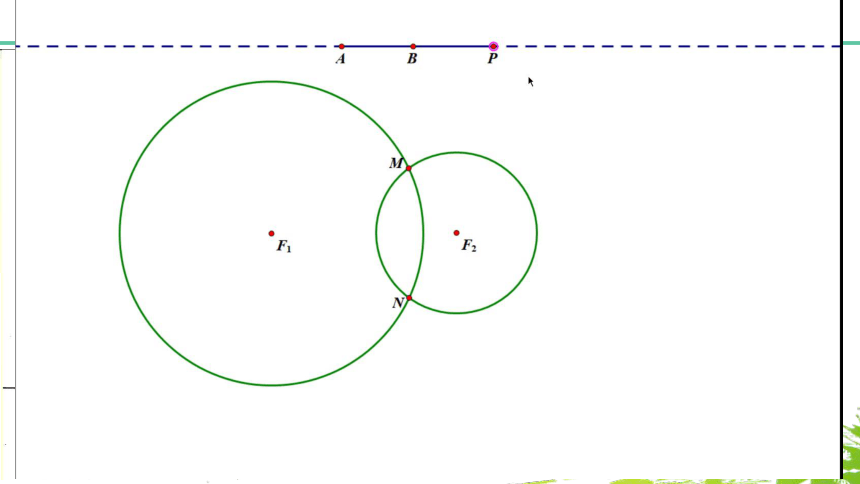
实验过程:取一条拉链,拉开它的一部分,在拉开的两边上各选择一点,分别固定在点F1、F2上,把笔尖放在拉链处,也就是点M处,拉开闭拢拉链,笔尖经过的点是不是可画出点的轨迹?
1. |MF1|-|MF2|=2a
2. |MF2|-|MF1|=2a
小组实验探究:
平面内与两个定点F1、F2的距离之差的绝对值等于非零常数的点的轨迹就叫做双曲线。
双曲线的定义
绝对值
1. |MF1|-|MF2|=2a
2. |MF2|-|MF1|=2a
||MF1|-|MF2||=2a
非零常数
|MF1|+|MF2|=2a( 2a>2c>0) ,
三角形的两边之和大于第三边;两边之差小于第三边
||MF1|-|MF2||=2a<|F1F2|
平面内与两个定点F1、F2的距离之差的绝对值等于非零常数(小于|F1F2|)的点的轨迹就叫做双曲线。
1.若||MF1|-|MF2||=2a=|F1F2|,则轨迹是什么
两条射线
不表示任何轨迹
线段F1F2的垂直平分线
2.若||MF1|-|MF2||=2a>|F1F2|,则轨迹是什么
若||MF1|-|MF2||=2a=0,则轨迹是什么
这两个定点F1、F2叫做双曲线的焦点,
两焦点间的距离叫做双曲线的焦距。
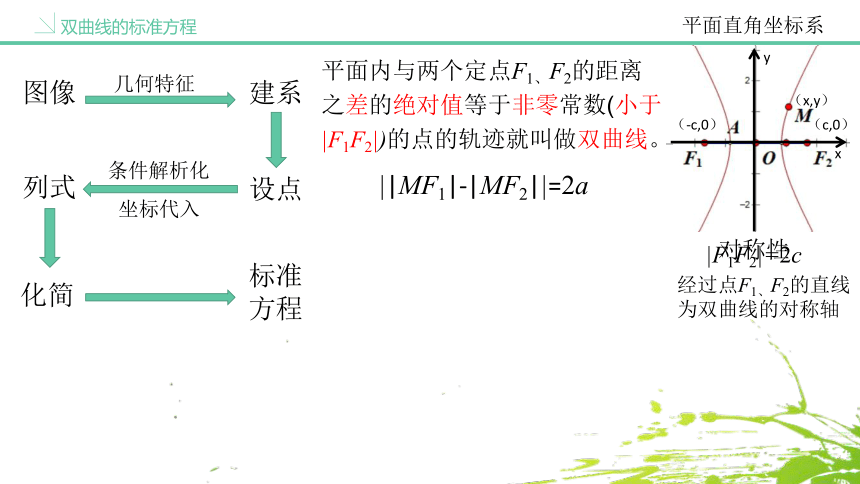
双曲线的标准方程
图像
建系
化简
标准方程
几何特征
设点
列式
条件解析化
坐标代入
x
y
对称性
经过点F1、F2的直线为双曲线的对称轴
平面直角坐标系
(x,y)
|F1F2|=2c
(-c,0)
(c,0)
||MF1|-|MF2||=2a
平面内与两个定点F1、F2的距离之差的绝对值等于非零常数(小于|F1F2|)的点的轨迹就叫做双曲线。
双曲线的标准方程
图像
建系
化简
标准方程
几何特征
设点
列式
条件解析化
坐标代入
x
y
平面直角坐标系
(x,y)
|F1F2|=2c
(-c,0)
(c,0)
||MF1|-|MF2||=2a
|MF1|=
|MF2|=
平面内与两个定点F1、F2的距离之差的绝对值等于非零常数(小于|F1F2|)的点的轨迹就叫做双曲线。
双曲线的标准方程
图像
建系
化简
标准方程
几何特征
设点
列式
条件解析化
坐标代入
x
y
平面直角坐标系
(x,y)
|F1F2|=2c
(-c,0)
(c,0)
||MF1|-|MF2||=2a
|MF1|=
|MF2|=
|-|=2a
平面内与两个定点F1、F2的距离之差的绝对值等于非零常数(小于|F1F2|)的点的轨迹就叫做双曲线。
双曲线的标准方程
图像
建系
化简
标准方程
几何特征
设点
列式
条件解析化
坐标代入
|-|=2a
双曲线的标准方程
图像
建系
化简
标准方程
几何特征
设点
列式
条件解析化
坐标代入
-=2a
双曲线的标准方程
图像
建系
化简
标准方程
几何特征
设点
列式
条件解析化
坐标代入
-=2a
=2a+
平方
双曲线的标准方程
图像
建系
化简
标准方程
几何特征
设点
列式
条件解析化
坐标代入
-=2a
=2a+
平方
=a
平方
双曲线的标准方程
图像
建系
化简
标准方程
几何特征
设点
列式
条件解析化
坐标代入
-=2a
=2a+
平方
=a
平方
=
求椭圆
标准方程
双曲线的标准方程
图像
建系
化简
标准方程
几何特征
设点
列式
条件解析化
坐标代入
-=2a
=2a+
平方
=a
平方
=
令
求椭圆
标准方程
双曲线的标准方程
图像
建系
化简
标准方程
几何特征
设点
列式
条件解析化
坐标代入
-=2a
=2a+
平方
=a
平方
=
令
求椭圆
标准方程
令
?
||MF1|-|MF2||=2a<|F1F2|
2a<2c
|F1F2|=2c
双曲线的标准方程
图像
建系
化简
标准方程
几何特征
设点
列式
条件解析化
坐标代入
-=2a
=2a+
平方
=a
平方
=
令
求椭圆
标准方程
令
?
||MF1|-|MF2||=2a<|F1F2|
2a<2c
|F1F2|=2c
双曲线的标准方程
图像
建系
化简
标准方程
几何特征
设点
列式
条件解析化
坐标代入
-=2a
=2a+
平方
=a
平方
=
令
令
焦点在y轴上的双曲线标准方程又长什么样子呢?
双曲线的标准方程
双曲线的标准方程
思考:双曲线的焦点位置和方程形式有什么关系?
双曲线的标准方程
思考:双曲线的焦点位置和方程形式有什么关系?
看前的系数,哪一个为正,焦点就在哪根轴上。
双曲线与椭圆之间的区别与联系
03
巩固练习
04
课堂小结
平面内与两个定点F1、F2的距离之差的绝对值等于非零常数(小于|F1F2|)的点的轨迹就叫做双曲线。
1.双曲线的定义:
2.双曲线的基本方程:
类比
坐标法
04
课堂小结
平面内与两个定点F1、F2的距离之差的绝对值等于非零常数(小于|F1F2|)的点的轨迹就叫做双曲线。
1.双曲线的定义:
2.双曲线的基本方程:
坐标法
类比
05
作业布置
P121的四道练习题T1,2,3,4;
作业本上相应的章节。
PUBLIC CLASS TEACHER
click on add related title wordsclick on add related title wordsclick on add related title words
thank you
3.2.1双曲线
及其标准方程
04
02
回顾旧知
01
巩固练习
03
新知导入
课堂小结
目 录
作业布置
05
01
回顾旧知
椭圆的定义是什么?
平面内与两个定点F1、F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆。
椭圆的基本方程是什么?
|MF1|+|MF2|=2a( 2a>2c>0) ,
点M的轨迹是椭圆;
若2a=2c ,
点M的轨迹是线段F1F2;
若2a<2c ,
点M的轨迹不存在。
三角形的两边之和大于第三边;两边之差小于第三边
02
新知导入
平面内与两个定点F1、F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆。
平面内与两个定点F1、F2的距离的差为非零常数的点的轨迹叫什么呢?
02
新知导入
小组实验探究:
材料:拉链,木板,纸,笔,图钉
实验过程:取一条拉链,拉开它的一部分,在拉开的两边上各选择一点,分别固定在点F1、F2上,把笔尖放在拉链处,也就是点M处,拉开闭拢拉链,笔尖经过的点是不是可画出点的轨迹?
1. |MF1|-|MF2|=2a
2. |MF2|-|MF1|=2a
小组实验探究:
平面内与两个定点F1、F2的距离之差的绝对值等于非零常数的点的轨迹就叫做双曲线。
双曲线的定义
绝对值
1. |MF1|-|MF2|=2a
2. |MF2|-|MF1|=2a
||MF1|-|MF2||=2a
非零常数
|MF1|+|MF2|=2a( 2a>2c>0) ,
三角形的两边之和大于第三边;两边之差小于第三边
||MF1|-|MF2||=2a<|F1F2|
平面内与两个定点F1、F2的距离之差的绝对值等于非零常数(小于|F1F2|)的点的轨迹就叫做双曲线。
1.若||MF1|-|MF2||=2a=|F1F2|,则轨迹是什么
两条射线
不表示任何轨迹
线段F1F2的垂直平分线
2.若||MF1|-|MF2||=2a>|F1F2|,则轨迹是什么
若||MF1|-|MF2||=2a=0,则轨迹是什么
这两个定点F1、F2叫做双曲线的焦点,
两焦点间的距离叫做双曲线的焦距。
双曲线的标准方程
图像
建系
化简
标准方程
几何特征
设点
列式
条件解析化
坐标代入
x
y
对称性
经过点F1、F2的直线为双曲线的对称轴
平面直角坐标系
(x,y)
|F1F2|=2c
(-c,0)
(c,0)
||MF1|-|MF2||=2a
平面内与两个定点F1、F2的距离之差的绝对值等于非零常数(小于|F1F2|)的点的轨迹就叫做双曲线。
双曲线的标准方程
图像
建系
化简
标准方程
几何特征
设点
列式
条件解析化
坐标代入
x
y
平面直角坐标系
(x,y)
|F1F2|=2c
(-c,0)
(c,0)
||MF1|-|MF2||=2a
|MF1|=
|MF2|=
平面内与两个定点F1、F2的距离之差的绝对值等于非零常数(小于|F1F2|)的点的轨迹就叫做双曲线。
双曲线的标准方程
图像
建系
化简
标准方程
几何特征
设点
列式
条件解析化
坐标代入
x
y
平面直角坐标系
(x,y)
|F1F2|=2c
(-c,0)
(c,0)
||MF1|-|MF2||=2a
|MF1|=
|MF2|=
|-|=2a
平面内与两个定点F1、F2的距离之差的绝对值等于非零常数(小于|F1F2|)的点的轨迹就叫做双曲线。
双曲线的标准方程
图像
建系
化简
标准方程
几何特征
设点
列式
条件解析化
坐标代入
|-|=2a
双曲线的标准方程
图像
建系
化简
标准方程
几何特征
设点
列式
条件解析化
坐标代入
-=2a
双曲线的标准方程
图像
建系
化简
标准方程
几何特征
设点
列式
条件解析化
坐标代入
-=2a
=2a+
平方
双曲线的标准方程
图像
建系
化简
标准方程
几何特征
设点
列式
条件解析化
坐标代入
-=2a
=2a+
平方
=a
平方
双曲线的标准方程
图像
建系
化简
标准方程
几何特征
设点
列式
条件解析化
坐标代入
-=2a
=2a+
平方
=a
平方
=
求椭圆
标准方程
双曲线的标准方程
图像
建系
化简
标准方程
几何特征
设点
列式
条件解析化
坐标代入
-=2a
=2a+
平方
=a
平方
=
令
求椭圆
标准方程
双曲线的标准方程
图像
建系
化简
标准方程
几何特征
设点
列式
条件解析化
坐标代入
-=2a
=2a+
平方
=a
平方
=
令
求椭圆
标准方程
令
?
||MF1|-|MF2||=2a<|F1F2|
2a<2c
|F1F2|=2c
双曲线的标准方程
图像
建系
化简
标准方程
几何特征
设点
列式
条件解析化
坐标代入
-=2a
=2a+
平方
=a
平方
=
令
求椭圆
标准方程
令
?
||MF1|-|MF2||=2a<|F1F2|
2a<2c
|F1F2|=2c
双曲线的标准方程
图像
建系
化简
标准方程
几何特征
设点
列式
条件解析化
坐标代入
-=2a
=2a+
平方
=a
平方
=
令
令
焦点在y轴上的双曲线标准方程又长什么样子呢?
双曲线的标准方程
双曲线的标准方程
思考:双曲线的焦点位置和方程形式有什么关系?
双曲线的标准方程
思考:双曲线的焦点位置和方程形式有什么关系?
看前的系数,哪一个为正,焦点就在哪根轴上。
双曲线与椭圆之间的区别与联系
03
巩固练习
04
课堂小结
平面内与两个定点F1、F2的距离之差的绝对值等于非零常数(小于|F1F2|)的点的轨迹就叫做双曲线。
1.双曲线的定义:
2.双曲线的基本方程:
类比
坐标法
04
课堂小结
平面内与两个定点F1、F2的距离之差的绝对值等于非零常数(小于|F1F2|)的点的轨迹就叫做双曲线。
1.双曲线的定义:
2.双曲线的基本方程:
坐标法
类比
05
作业布置
P121的四道练习题T1,2,3,4;
作业本上相应的章节。
PUBLIC CLASS TEACHER
click on add related title wordsclick on add related title wordsclick on add related title words
thank you
