2023年人教版数学七年级下册期末复习 第七章《平面直角坐标系》单元复习(含答案)
文档属性
| 名称 | 2023年人教版数学七年级下册期末复习 第七章《平面直角坐标系》单元复习(含答案) | 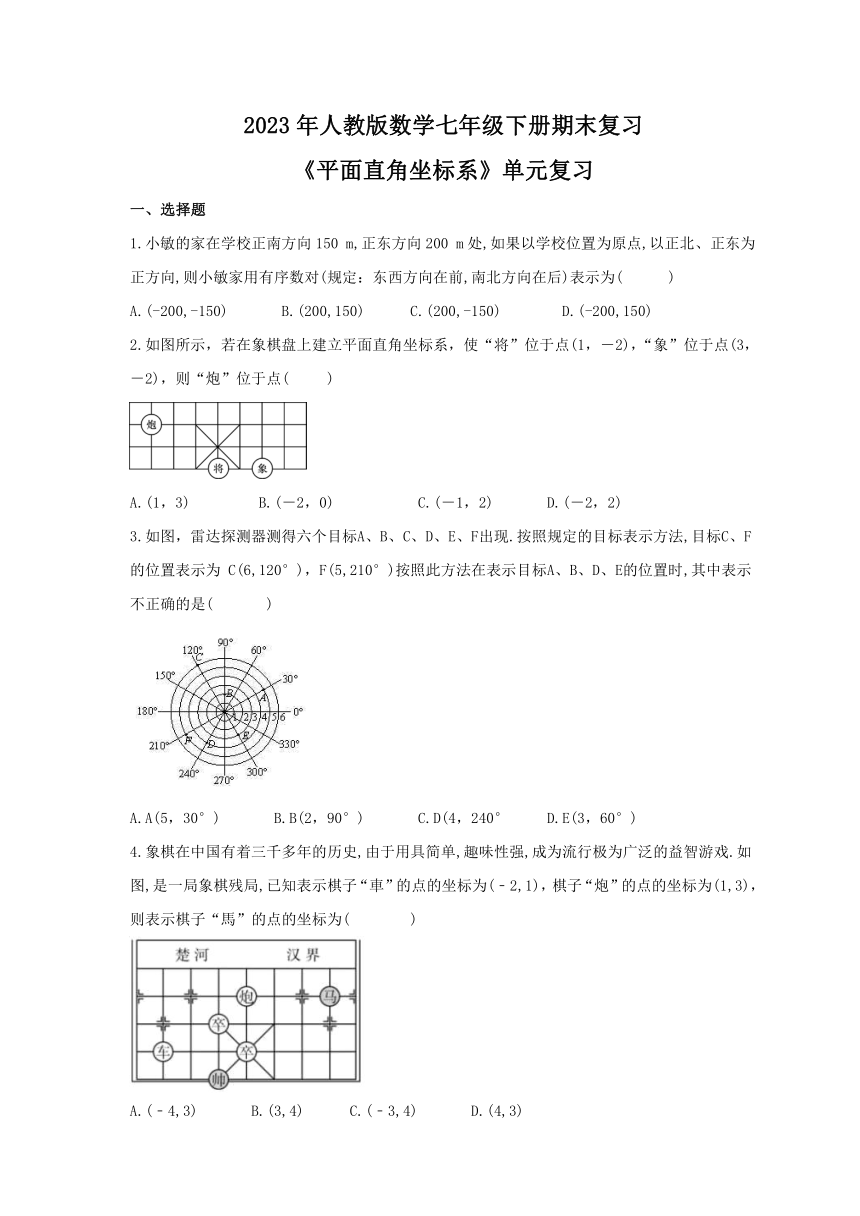 | |
| 格式 | docx | ||
| 文件大小 | 229.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-03 15:01:02 | ||
图片预览



文档简介
2023年人教版数学七年级下册期末复面直角坐标系》单元复习
一 、选择题
1.小敏的家在学校正南方向150 m,正东方向200 m处,如果以学校位置为原点,以正北、正东为正方向,则小敏家用有序数对(规定:东西方向在前,南北方向在后)表示为( )
A.(-200,-150) B.(200,150) C.(200,-150) D.(-200,150)
2.如图所示,若在象棋盘上建立平面直角坐标系,使“将”位于点(1,-2),“象”位于点(3,-2),则“炮”位于点( )
A.(1,3) B.(-2,0) C.(-1,2) D.(-2,2)
3.如图,雷达探测器测得六个目标A、B、C、D、E、F出现.按照规定的目标表示方法,目标C、F的位置表示为 C(6,120°),F(5,210°)按照此方法在表示目标A、B、D、E的位置时,其中表示不正确的是( )
A.A(5,30°) B.B(2,90°) C.D(4,240° D.E(3,60°)
4.象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“車”的点的坐标为(﹣2,1),棋子“炮”的点的坐标为(1,3),则表示棋子“馬”的点的坐标为( )
A.(﹣4,3) B.(3,4) C.(﹣3,4) D.(4,3)
5.若有点A和点B,坐标分别为A(3,2),B(2,3),则( )
A.A,B为同一个点 B.A,B为重合的两点
C.A,B为不重合的两点 D.无法确定
6.若m是任意实数,则点P (m-4,m+1) 一定不在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.若点P(a,b)在第三象限,则M(-ab,-a)应在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.已知点A(-4,-6),将点A先向右平移4个单位长度,再向上平移6个单位长度,得到A′,
则A′的坐标为( )
A.(0,0) B.(1,1) C.(2,2) D.(5,5)
9.如图,如果将三角形ABC向左平移2格得到三角形A′B′C′,则顶点A′的位置用数对表示为( )
A.(5,1) B.(1,1) C.(7,1) D.(3,3)
10.线段CD是由线段AB平移得到的,点A(﹣1,5)的对应点为C(4,8),则点B(﹣4,﹣2)的对应点D的坐标为( )
A.(﹣9,﹣5) B.(﹣9,1) C.(1,﹣5) D.(1,1)
11.已知三角形ABC平移后得到三角形A1B1C1 ,且A(-2,3),B(-4,-1),C1(m,n),C(m+5,n+3),则A1,B1两点的坐标为( )
A.(3,6),(1,2) B.(-7,0),(-9,-4)
C.(1,8),(-1,4) D.(-7,-2),(0,-9)
12.对点(x,y)的一次操作变换记为P1(x,y),定义其变换法则如下:P1(x,y)=(x+y,x﹣y);且规定Pn(x,y)=P1(Pn﹣1(x,y))(n为大于1的整数).如P1(1,2)=(3,﹣1),P2(1,2)=P1(P1(1,2))=P1(3,﹣1)=(2,4),P3(1,2)=P1(P2(1,2))=P1(2,4)=(6,﹣2).则P2027(1,﹣1)=( )
A.(0,21013) B.(0,﹣21013) C.(0,﹣21014) D.(0,21014)
二 、填空题
13.如图,在直角坐标系中,右边的蝴蝶是由左边的蝴蝶飞过去以后得到的,左图案中左右翅尖的坐标分别是(-4,2)、(-2,2),右图案中左翅尖的坐标是(3,4),则右图案中右翅尖的坐标是________.
14.如图,小刚在小明的北偏东60°方向的500 m处,则小明在小刚的 方向的 m.(请用方向和距离描述小明相对于小刚的位置)
15.若第二象限内的点P(x,y)满足|x|=3,y2=25,则点P的坐标是 .
16.已知点P(x,y)在第三象限,且|x|=,|y﹣2|=3,则点P的坐标为 .
17.在平面直角坐标系中,三角形ABC的三个顶点的横坐标保持不变,纵坐标都减去2个单位长度,则得到的新三角形与原三角形相比向 平移了 个单位长度.
18.如图,动点P从(0,3)出发,沿所示方向运动,每当碰到长方形的边时反弹,第一次碰到长方形的边时的位置为P1(3,0),当点P第2024次碰到长方形的边时,点P的坐标为 .
三 、解答题
19.如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度请回答下列问题:
(1)平移后的三个顶点坐标分别为:A1______,B1______,C1______;
(2)画出平移后三角形A1B1C1;
(3)求三角形ABC的面积.
20.如图,三角形ABC在平面直角坐标系中,将三角形ABC向左平移1个单位长度,再向上平移3个单位长度得到△A1B1C1,;
(1)请画出三角形A1B1C1,并写出三角形A1B1C1各顶点的坐标.
(2)求出三角形A1B1C1的面积.
21.已知点P(2m+4,m﹣1).试分别根据下列条件,求出点P的坐标.
(1)点P的纵坐标比横坐标大3;
(2)点P在过A(2,﹣3)点,且与x轴平行的直线上.
22.如图,三角形DEF是三角形ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点P(a+3b,4a-b)与点Q(2a-9,2b-9)也是通过上述变换得到的对应点,求a,b的值.
23.如图所示,△A′B′C′是△ABC经过平移得到的,A(﹣4,﹣1),B(﹣5,﹣4),C(﹣1,﹣3),△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).
(1)请写出三角形ABC平移的过程;
(2)分别写出点A′,B′,C′的坐标;
(3)求△A′B′C′的面积.
答案
1.C
2.B
3.D
4.D
5.C
6.D
7.B
8.A
9.B
10.D
11.B
12.D
13.答案为:(5,4).
14.答案为:南偏西60°方,500m.
15.答案为:(-3,5).
16.答案为:(﹣,﹣1).
17.答案为:下,2.
18.答案为:(7,4).
19.解:(1)A1(3,5),B1(0,0),C1(5,2);
(2)略;
(3)9.5;
20.解:(1)如图所示.
由图可知,A1(﹣2,2),B1(3,5),C1(0,6);
(2)S△A1B1C1=4×5﹣×5×3﹣×1×3﹣×2×4=20﹣﹣﹣4=7.
21.解:(1)∵点P(2m+4,m﹣1),点P的纵坐标比横坐标大3,
∴m﹣1﹣(2m+4)=3,解得:m=﹣8,
∴2m+4=﹣12,m﹣1=﹣9,
∴点P的坐标为:(﹣12,﹣9);
(2)∵点P在过A(2,﹣3)点,且与x轴平行的直线上,
∴m﹣1=﹣3,解得:m=﹣2,
∴2m+4=0,
∴P点坐标为:(0,﹣3).
22.解:(1)点A的坐标为(2,3),点D的坐标为(-2,-3),点B的坐标为(1,2),
点E的坐标为(-1,-2),点C的坐标为(3,1),点F的坐标为(-3,-1),
对应点的横、纵坐标分别互为相反数;
(2)由(1)得,a+3b+2a-9=0,4a-b+2b-9=0,解得,a=2,b=1,
答:a=2,b=1.
23.解:(1)∵△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4),
∴平移后对应点的横坐标加6,纵坐标加4,
∴△ABC先向右平移6个单位,再向上平移4个单位得到△A′B′C′
或△ABC先向上平移4个单位,再向右平移6个单位得到△A′B′C′;
(2)由(1)可知,A′(2,3),B′(1,0),C′(5,1);
(3)如图所示,S△A′B′C′=3×4﹣×1×3﹣×1×4﹣×2×3=5.5.
一 、选择题
1.小敏的家在学校正南方向150 m,正东方向200 m处,如果以学校位置为原点,以正北、正东为正方向,则小敏家用有序数对(规定:东西方向在前,南北方向在后)表示为( )
A.(-200,-150) B.(200,150) C.(200,-150) D.(-200,150)
2.如图所示,若在象棋盘上建立平面直角坐标系,使“将”位于点(1,-2),“象”位于点(3,-2),则“炮”位于点( )
A.(1,3) B.(-2,0) C.(-1,2) D.(-2,2)
3.如图,雷达探测器测得六个目标A、B、C、D、E、F出现.按照规定的目标表示方法,目标C、F的位置表示为 C(6,120°),F(5,210°)按照此方法在表示目标A、B、D、E的位置时,其中表示不正确的是( )
A.A(5,30°) B.B(2,90°) C.D(4,240° D.E(3,60°)
4.象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“車”的点的坐标为(﹣2,1),棋子“炮”的点的坐标为(1,3),则表示棋子“馬”的点的坐标为( )
A.(﹣4,3) B.(3,4) C.(﹣3,4) D.(4,3)
5.若有点A和点B,坐标分别为A(3,2),B(2,3),则( )
A.A,B为同一个点 B.A,B为重合的两点
C.A,B为不重合的两点 D.无法确定
6.若m是任意实数,则点P (m-4,m+1) 一定不在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.若点P(a,b)在第三象限,则M(-ab,-a)应在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.已知点A(-4,-6),将点A先向右平移4个单位长度,再向上平移6个单位长度,得到A′,
则A′的坐标为( )
A.(0,0) B.(1,1) C.(2,2) D.(5,5)
9.如图,如果将三角形ABC向左平移2格得到三角形A′B′C′,则顶点A′的位置用数对表示为( )
A.(5,1) B.(1,1) C.(7,1) D.(3,3)
10.线段CD是由线段AB平移得到的,点A(﹣1,5)的对应点为C(4,8),则点B(﹣4,﹣2)的对应点D的坐标为( )
A.(﹣9,﹣5) B.(﹣9,1) C.(1,﹣5) D.(1,1)
11.已知三角形ABC平移后得到三角形A1B1C1 ,且A(-2,3),B(-4,-1),C1(m,n),C(m+5,n+3),则A1,B1两点的坐标为( )
A.(3,6),(1,2) B.(-7,0),(-9,-4)
C.(1,8),(-1,4) D.(-7,-2),(0,-9)
12.对点(x,y)的一次操作变换记为P1(x,y),定义其变换法则如下:P1(x,y)=(x+y,x﹣y);且规定Pn(x,y)=P1(Pn﹣1(x,y))(n为大于1的整数).如P1(1,2)=(3,﹣1),P2(1,2)=P1(P1(1,2))=P1(3,﹣1)=(2,4),P3(1,2)=P1(P2(1,2))=P1(2,4)=(6,﹣2).则P2027(1,﹣1)=( )
A.(0,21013) B.(0,﹣21013) C.(0,﹣21014) D.(0,21014)
二 、填空题
13.如图,在直角坐标系中,右边的蝴蝶是由左边的蝴蝶飞过去以后得到的,左图案中左右翅尖的坐标分别是(-4,2)、(-2,2),右图案中左翅尖的坐标是(3,4),则右图案中右翅尖的坐标是________.
14.如图,小刚在小明的北偏东60°方向的500 m处,则小明在小刚的 方向的 m.(请用方向和距离描述小明相对于小刚的位置)
15.若第二象限内的点P(x,y)满足|x|=3,y2=25,则点P的坐标是 .
16.已知点P(x,y)在第三象限,且|x|=,|y﹣2|=3,则点P的坐标为 .
17.在平面直角坐标系中,三角形ABC的三个顶点的横坐标保持不变,纵坐标都减去2个单位长度,则得到的新三角形与原三角形相比向 平移了 个单位长度.
18.如图,动点P从(0,3)出发,沿所示方向运动,每当碰到长方形的边时反弹,第一次碰到长方形的边时的位置为P1(3,0),当点P第2024次碰到长方形的边时,点P的坐标为 .
三 、解答题
19.如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度请回答下列问题:
(1)平移后的三个顶点坐标分别为:A1______,B1______,C1______;
(2)画出平移后三角形A1B1C1;
(3)求三角形ABC的面积.
20.如图,三角形ABC在平面直角坐标系中,将三角形ABC向左平移1个单位长度,再向上平移3个单位长度得到△A1B1C1,;
(1)请画出三角形A1B1C1,并写出三角形A1B1C1各顶点的坐标.
(2)求出三角形A1B1C1的面积.
21.已知点P(2m+4,m﹣1).试分别根据下列条件,求出点P的坐标.
(1)点P的纵坐标比横坐标大3;
(2)点P在过A(2,﹣3)点,且与x轴平行的直线上.
22.如图,三角形DEF是三角形ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点P(a+3b,4a-b)与点Q(2a-9,2b-9)也是通过上述变换得到的对应点,求a,b的值.
23.如图所示,△A′B′C′是△ABC经过平移得到的,A(﹣4,﹣1),B(﹣5,﹣4),C(﹣1,﹣3),△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).
(1)请写出三角形ABC平移的过程;
(2)分别写出点A′,B′,C′的坐标;
(3)求△A′B′C′的面积.
答案
1.C
2.B
3.D
4.D
5.C
6.D
7.B
8.A
9.B
10.D
11.B
12.D
13.答案为:(5,4).
14.答案为:南偏西60°方,500m.
15.答案为:(-3,5).
16.答案为:(﹣,﹣1).
17.答案为:下,2.
18.答案为:(7,4).
19.解:(1)A1(3,5),B1(0,0),C1(5,2);
(2)略;
(3)9.5;
20.解:(1)如图所示.
由图可知,A1(﹣2,2),B1(3,5),C1(0,6);
(2)S△A1B1C1=4×5﹣×5×3﹣×1×3﹣×2×4=20﹣﹣﹣4=7.
21.解:(1)∵点P(2m+4,m﹣1),点P的纵坐标比横坐标大3,
∴m﹣1﹣(2m+4)=3,解得:m=﹣8,
∴2m+4=﹣12,m﹣1=﹣9,
∴点P的坐标为:(﹣12,﹣9);
(2)∵点P在过A(2,﹣3)点,且与x轴平行的直线上,
∴m﹣1=﹣3,解得:m=﹣2,
∴2m+4=0,
∴P点坐标为:(0,﹣3).
22.解:(1)点A的坐标为(2,3),点D的坐标为(-2,-3),点B的坐标为(1,2),
点E的坐标为(-1,-2),点C的坐标为(3,1),点F的坐标为(-3,-1),
对应点的横、纵坐标分别互为相反数;
(2)由(1)得,a+3b+2a-9=0,4a-b+2b-9=0,解得,a=2,b=1,
答:a=2,b=1.
23.解:(1)∵△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4),
∴平移后对应点的横坐标加6,纵坐标加4,
∴△ABC先向右平移6个单位,再向上平移4个单位得到△A′B′C′
或△ABC先向上平移4个单位,再向右平移6个单位得到△A′B′C′;
(2)由(1)可知,A′(2,3),B′(1,0),C′(5,1);
(3)如图所示,S△A′B′C′=3×4﹣×1×3﹣×1×4﹣×2×3=5.5.
