人教版(2019)新教材高中物理选择性必修1 2.4 单摆(2)课件(共39张PPT)
文档属性
| 名称 | 人教版(2019)新教材高中物理选择性必修1 2.4 单摆(2)课件(共39张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 7.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-05-02 00:00:00 | ||
图片预览








文档简介
(共39张PPT)
单摆
日常生活中的摆
日常生活中的摆
日常生活中的摆
实验室中的摆
【问题1】小球的摆动是否为简谐运动呢?
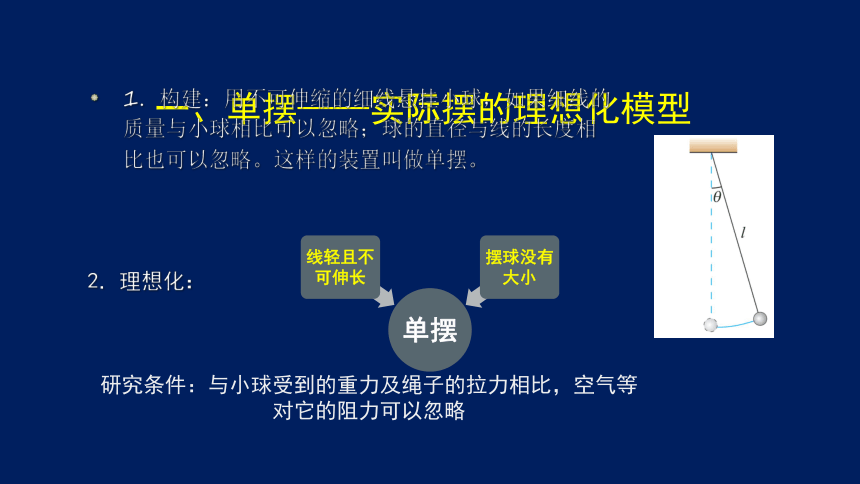
一、单摆——实际摆的理想化模型
1.构建:用不可伸缩的细线悬挂小球,如果细线的质量与小球相比可以忽略;球的直径与线的长度相比也可以忽略。这样的装置叫做单摆。
2.理想化:
研究条件:与小球受到的重力及绳子的拉力相比,空气等对它的阻力可以忽略
【问题2】用什么方法探究单摆的振动是否为简谐运动?
方案一:尝试画出沙摆振动的图像
方案一:尝试画出单摆振动的图像
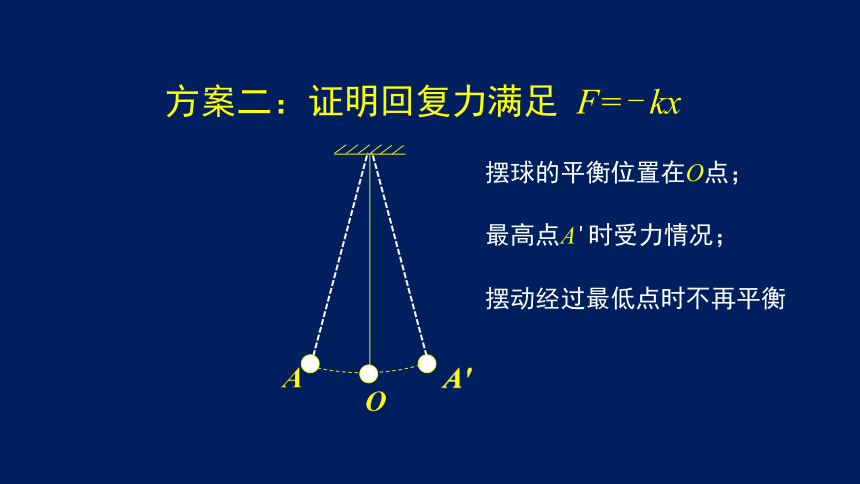
方案二:证明回复力满足 F=- kx
O
A'
A
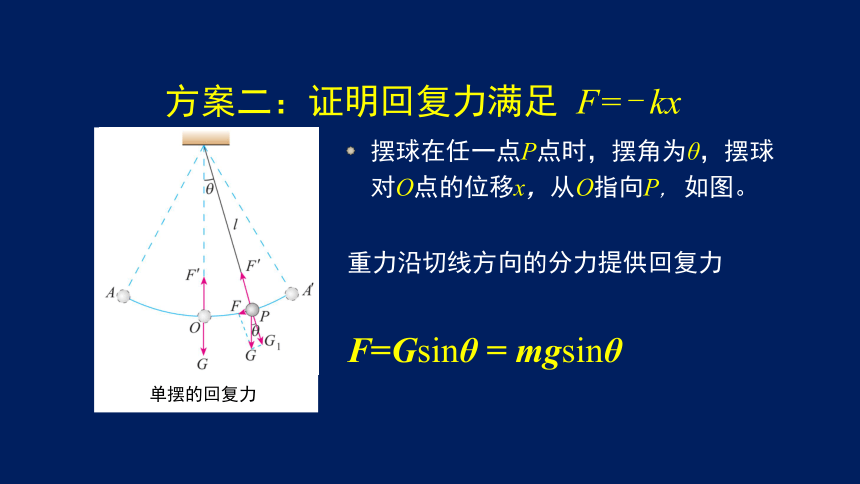
方案二:证明回复力满足 F=- kx
摆球在任一点P点时,摆角为θ,摆球对O点的位移x,从O指向P, 如图。
F=Gsinθ = mgsinθ
重力沿切线方向的分力提供回复力
单摆的回复力
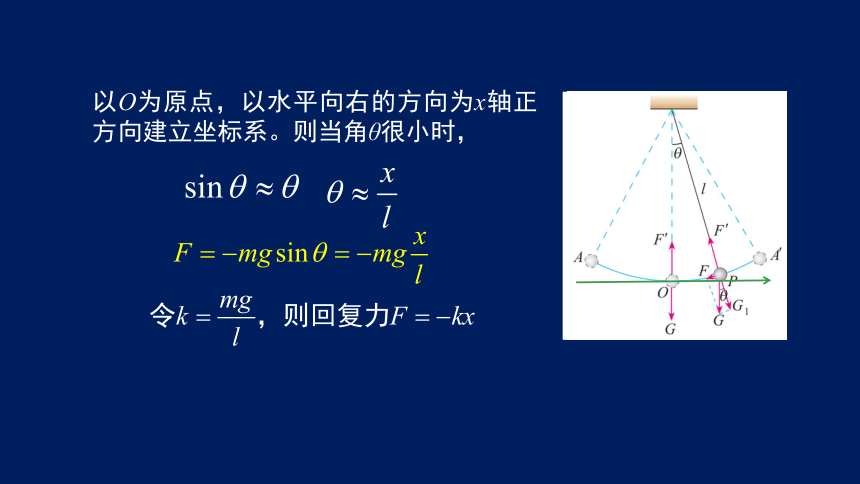
以O为原点,以水平向右的方向为x轴正方向建立坐标系。则当角θ很小时,
结 论
问题3:单摆做简谐运动时,其周期与哪些因素有关系呢
猜想
振幅、质量、摆长
问题3:单摆做简谐运动时,其周期与哪些因素有关系呢
猜想
振幅、质量、摆长
设计方案
控制变量思想
实验设计
用游标卡尺测钢球的外径
摆长的测量方法
用米尺测量摆线从悬点到钢球的距离,注意测量时保持竖直,同时摆线保持张紧,因为这样测量的数据才更接近在摆动时的摆线长。
摆长=摆线长+钢球半径
猜想
振幅、质量、摆长
设计方案
控制变量思想
实施探究
数据记录与处理
问题3:单摆做简谐运动时,其周期与哪些因素有关系呢
探究一:探究周期与振幅的关系
次数 1 2 3 4 5 6
20次全振动时间/s 37.72 37.78 37.82 37.65 37.83 37.84
周期/s 1.886 1.889 1.891 1.883 1.892 1.892
实验表明:单摆周期与振幅无关,这是摆的等时性。
伽利略:吊灯摆动的启示
探究二:探究周期与摆球质量的关系
实验思想:相同摆长,相同尺寸、不同质量的摆球。
实验表明:单摆周期与摆球质量无关
问题4:单摆做简谐运动时,其周期与摆长有怎样的关系呢?
问题4:单摆做简谐运动时,其周期与摆长有怎样的关系呢?
探究三:探究周期与摆长的关系
探究三:探究周期与摆长的关系
实验次数 线长cm 半径cm 摆长cm 周期T(s) 20次周期(s)
1 30.00 0.95 30.95 1.12 22.32
5 48.95 0.95 49.90 1.42 28.34
9 76.00 0.95 76.95 1.76 35.15
10 81.80 0.95 82.75 1.82 36.44
13 93.00 0.95 93.95 1.95 38.98
16 108.50 0.95 109.45 2.10 41.98
19 135.00 0.95 135.95 2.34 46.78
探究三:探究周期与摆长的关系
y轴:周期T
x轴:摆长l
探究三:探究周期与摆长的关系
y轴:周期T
x轴:摆长的平方l2
探究三:探究周期与摆长的关系
y轴:周期的平方T2
x轴:摆长l
单摆的周期
该式是个近似公式,由它算出的周期与精确值之间的差别随着偏角的增加而增加。当偏角为5 两者相差0.01%
第一座摆钟
从日晷到原子钟
回顾人类计时工具的发展,从日晷、水钟、沙漏等人造计时装置,到钟摆的出现,再到石英晶体钟和原子钟。到目前为止,地面上精度最高的冷原子喷泉钟已经达到每 3 亿年只有1 s 的误差,更高精度的冷原子光钟也在快速发展中。
我国制造的空间冷原子钟,这是原子钟发展史上又一个重大突破。
单摆周期的应用
(1)计时器:利用等时性
惠更斯在1656年首先利用摆的等时性发明了带摆的计时器(1657年获得专利权)
(2)测定当地的重力加速度
小 结
案例一、理解单摆运动中的动力学原理
1.关于单摆,下列说法中正确的是( )
A.摆球运动的回复力是摆线张力和重力的合力
B.摆球在运动过程中经过轨迹上的同一点时,加速度相等
C.摆球在运动过程中,加速度的方向始终指向平衡位置
D.摆球经过平衡位置时,加速度为零
B
建模→两个分析:受力分析、运动分析
A'
A
案例二、认识秒摆及其拓展应用
2.周期是 2 s 的单摆叫秒摆,秒摆的摆长是多少?把一个地球上的秒摆拿到月球上去,已知月球上的自由落体加速度为 1.6 m/s2 ,它在月球上做 50 次全振动要用多少时间?
分析与解答
由周期公式
,推导出摆长表达式
代入数据得摆长约为1m。
依题可得,这个摆在月球上
所在在月球上做50次全振动要用250s
思考:在山脚下走时准确的钟摆,拿到一个较高的山顶上后,振动周期如何变化呢?
3.一条细线下面挂着一个小球,让它自由摆动,画出它的振动图像如图所示。
(1) 请根据图中的数据计算出它的摆长。
(2) 请根据图中的数据估算出它摆动的最大偏角。
图像→图景
分析与解答
(2)其摆角最大时,摆球处于振幅位置。
由图可知,摆球振幅为0.04cm,
远小于摆长,因此,
最大偏角的正弦值为
角θ的弧度值约为0.04
单摆
日常生活中的摆
日常生活中的摆
日常生活中的摆
实验室中的摆
【问题1】小球的摆动是否为简谐运动呢?
一、单摆——实际摆的理想化模型
1.构建:用不可伸缩的细线悬挂小球,如果细线的质量与小球相比可以忽略;球的直径与线的长度相比也可以忽略。这样的装置叫做单摆。
2.理想化:
研究条件:与小球受到的重力及绳子的拉力相比,空气等对它的阻力可以忽略
【问题2】用什么方法探究单摆的振动是否为简谐运动?
方案一:尝试画出沙摆振动的图像
方案一:尝试画出单摆振动的图像
方案二:证明回复力满足 F=- kx
O
A'
A
方案二:证明回复力满足 F=- kx
摆球在任一点P点时,摆角为θ,摆球对O点的位移x,从O指向P, 如图。
F=Gsinθ = mgsinθ
重力沿切线方向的分力提供回复力
单摆的回复力
以O为原点,以水平向右的方向为x轴正方向建立坐标系。则当角θ很小时,
结 论
问题3:单摆做简谐运动时,其周期与哪些因素有关系呢
猜想
振幅、质量、摆长
问题3:单摆做简谐运动时,其周期与哪些因素有关系呢
猜想
振幅、质量、摆长
设计方案
控制变量思想
实验设计
用游标卡尺测钢球的外径
摆长的测量方法
用米尺测量摆线从悬点到钢球的距离,注意测量时保持竖直,同时摆线保持张紧,因为这样测量的数据才更接近在摆动时的摆线长。
摆长=摆线长+钢球半径
猜想
振幅、质量、摆长
设计方案
控制变量思想
实施探究
数据记录与处理
问题3:单摆做简谐运动时,其周期与哪些因素有关系呢
探究一:探究周期与振幅的关系
次数 1 2 3 4 5 6
20次全振动时间/s 37.72 37.78 37.82 37.65 37.83 37.84
周期/s 1.886 1.889 1.891 1.883 1.892 1.892
实验表明:单摆周期与振幅无关,这是摆的等时性。
伽利略:吊灯摆动的启示
探究二:探究周期与摆球质量的关系
实验思想:相同摆长,相同尺寸、不同质量的摆球。
实验表明:单摆周期与摆球质量无关
问题4:单摆做简谐运动时,其周期与摆长有怎样的关系呢?
问题4:单摆做简谐运动时,其周期与摆长有怎样的关系呢?
探究三:探究周期与摆长的关系
探究三:探究周期与摆长的关系
实验次数 线长cm 半径cm 摆长cm 周期T(s) 20次周期(s)
1 30.00 0.95 30.95 1.12 22.32
5 48.95 0.95 49.90 1.42 28.34
9 76.00 0.95 76.95 1.76 35.15
10 81.80 0.95 82.75 1.82 36.44
13 93.00 0.95 93.95 1.95 38.98
16 108.50 0.95 109.45 2.10 41.98
19 135.00 0.95 135.95 2.34 46.78
探究三:探究周期与摆长的关系
y轴:周期T
x轴:摆长l
探究三:探究周期与摆长的关系
y轴:周期T
x轴:摆长的平方l2
探究三:探究周期与摆长的关系
y轴:周期的平方T2
x轴:摆长l
单摆的周期
该式是个近似公式,由它算出的周期与精确值之间的差别随着偏角的增加而增加。当偏角为5 两者相差0.01%
第一座摆钟
从日晷到原子钟
回顾人类计时工具的发展,从日晷、水钟、沙漏等人造计时装置,到钟摆的出现,再到石英晶体钟和原子钟。到目前为止,地面上精度最高的冷原子喷泉钟已经达到每 3 亿年只有1 s 的误差,更高精度的冷原子光钟也在快速发展中。
我国制造的空间冷原子钟,这是原子钟发展史上又一个重大突破。
单摆周期的应用
(1)计时器:利用等时性
惠更斯在1656年首先利用摆的等时性发明了带摆的计时器(1657年获得专利权)
(2)测定当地的重力加速度
小 结
案例一、理解单摆运动中的动力学原理
1.关于单摆,下列说法中正确的是( )
A.摆球运动的回复力是摆线张力和重力的合力
B.摆球在运动过程中经过轨迹上的同一点时,加速度相等
C.摆球在运动过程中,加速度的方向始终指向平衡位置
D.摆球经过平衡位置时,加速度为零
B
建模→两个分析:受力分析、运动分析
A'
A
案例二、认识秒摆及其拓展应用
2.周期是 2 s 的单摆叫秒摆,秒摆的摆长是多少?把一个地球上的秒摆拿到月球上去,已知月球上的自由落体加速度为 1.6 m/s2 ,它在月球上做 50 次全振动要用多少时间?
分析与解答
由周期公式
,推导出摆长表达式
代入数据得摆长约为1m。
依题可得,这个摆在月球上
所在在月球上做50次全振动要用250s
思考:在山脚下走时准确的钟摆,拿到一个较高的山顶上后,振动周期如何变化呢?
3.一条细线下面挂着一个小球,让它自由摆动,画出它的振动图像如图所示。
(1) 请根据图中的数据计算出它的摆长。
(2) 请根据图中的数据估算出它摆动的最大偏角。
图像→图景
分析与解答
(2)其摆角最大时,摆球处于振幅位置。
由图可知,摆球振幅为0.04cm,
远小于摆长,因此,
最大偏角的正弦值为
角θ的弧度值约为0.04
