相似三角形[下学期]
图片预览


文档简介
课件14张PPT。2019/3/1512019/3/152复习:1、相似多边形的特征;对应边成比例,对应角相等。2、识别两个多边形相似的方法: 对应边成比例,对应角相等
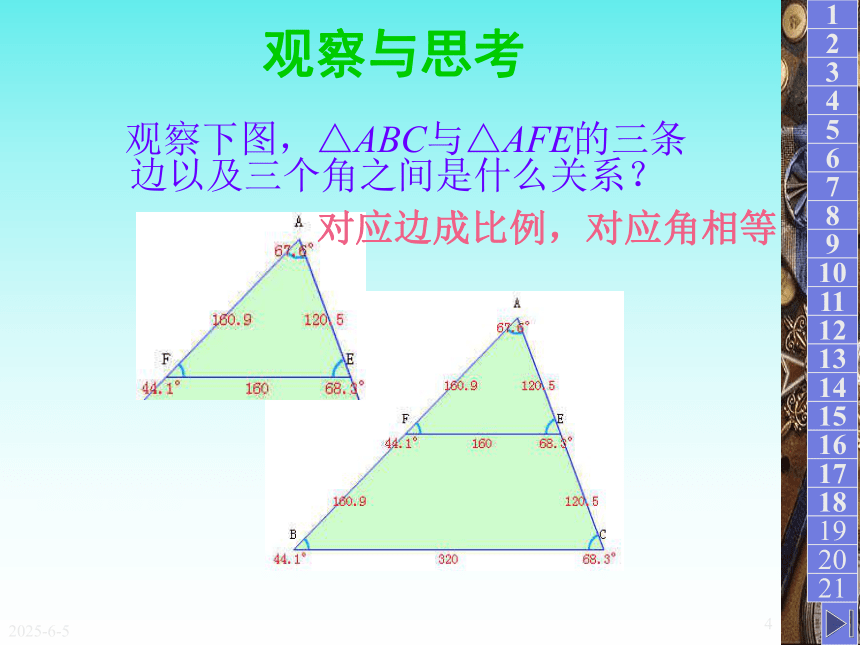
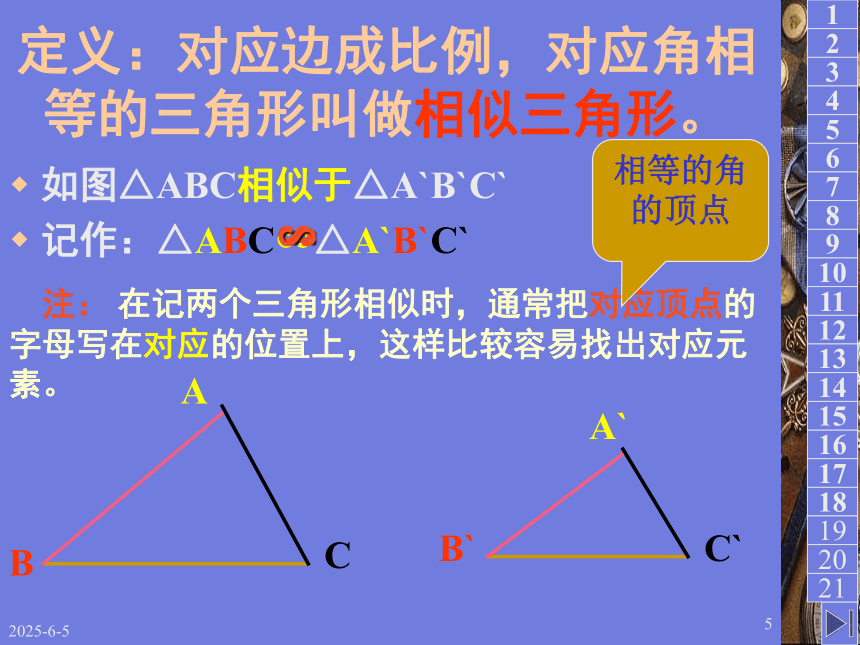
的两个多边形相似。2019/3/153问题 1985年著名建筑大师贝聿铭在设计巴黎卢浮宫前玻璃金字塔时需要先设计一个小模型,模型侧面三角形与实际建筑侧面三角形形状相同,但大小不等 . 这两个三角形是什么关系?2019/3/154观察与思考 观察下图,△ABC与△AFE的三条边以及三个角之间是什么关系? 对应边成比例,对应角相等2019/3/155定义:对应边成比例,对应角相等的三角形叫做相似三角形。如图△ABC相似于△A`B`C`
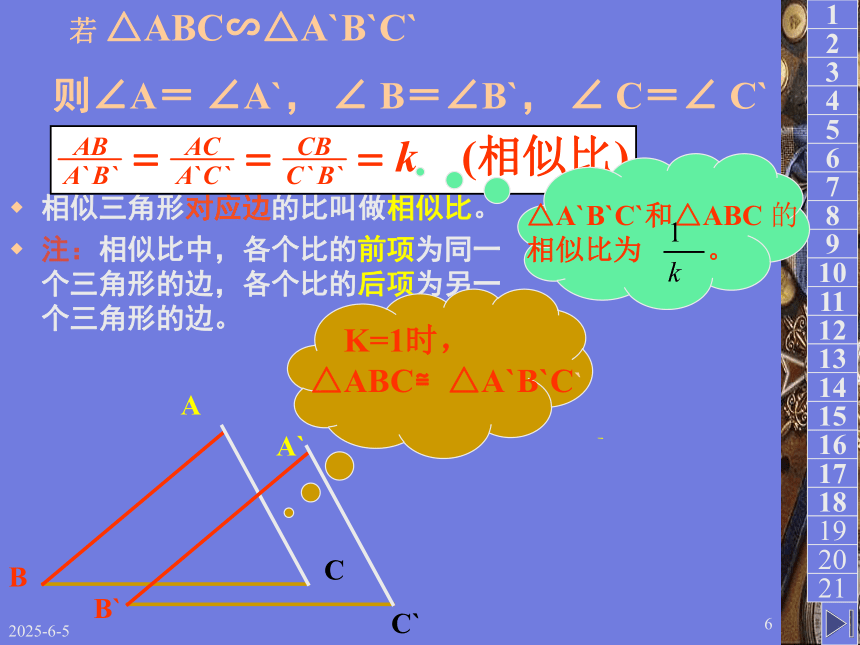
记作:△ABC∽△A`B`C` 注: 在记两个三角形相似时,通常把对应顶点的字母写在对应的位置上,这样比较容易找出对应元素。相等的角的顶点∽∽∽∽2019/3/156则∠A= ∠A`, ∠ B=∠B`, ∠ C=∠ C` 相似三角形对应边的比叫做相似比。
注:相似比中,各个比的前项为同一个三角形的边,各个比的后项为另一个三角形的边。 若 △ABC∽△A`B`C` △A`B`C`和△ABC 的
相似比为 。 K=1时,
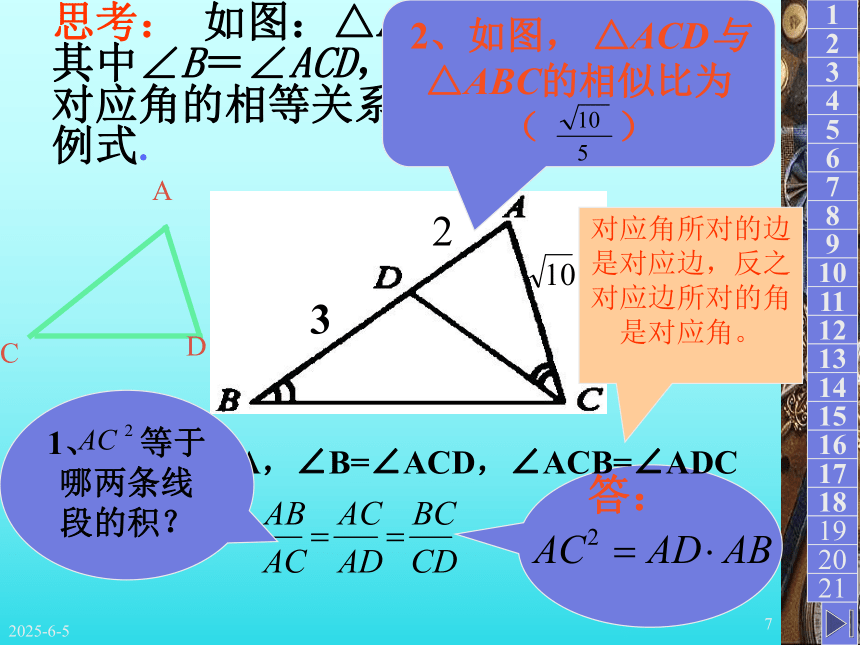
△ABC≌△A`B`C`A`B`C`2019/3/157 思考: 如图:△ABC∽ △ACD,其中∠B=∠ACD,请写出它们的对应角的相等关系及对应边的比例式. 解:∠A=∠A,∠B=∠ACD,∠ACB=∠ADC对应角所对的边是对应边,反之对应边所对的角是对应角。ACD23答:2、如图, △ACD与 △ABC的相似比为( )1、 等于哪两条线段的积?2019/3/158判断1.若△ABC∽△A`B`C`,则
AB:BC:AC=A`B`:B`C`:A`C`
2.若△ABC∽△A`B`C`,且B`C`=3, BC=5,则相似比为3:5。
3.全等三角形一定相似。
4.所有的等腰三角形都相似。
5.所有的等边三角形都相似。
6.所有的直角三角形都相似。√×√√××正确答案: 5:32019/3/159相似比为填空:1.△ABC中,AB=6,BC=4,CA=9,且△ABC∽△A`B`C`,△A`B`C`的最短边的长为8,则最长边的长为( )
2、 △ABC∽△A`B`C`,∠A=400,∠B=1100,则∠C`=( )0。
3、 △ABC∽△A`B`C` ,△ABC的三边长分别是 3、4、5,且 △A`B`C`的最大边长为15,则△A`B`C`的周长为( ), △ABC与△A`B`C`的周长的比为( )。
183036注意 “对应”∠C=相似比为2019/3/1510解:∠A=∠A,
∠ADE=∠B,
∠AED=∠C。
解:∠DAE=∠BAC,
∠D=∠B,
∠E=∠C。关解答ADE2019/3/1511解:∠A=∠A,
∠AED=∠B,
∠ADE=∠C。AED2019/3/1512A选择2019/3/1513B2019/3/15141.相似三角形的定义:对应角相等,对应边成比例的三角形叫做相似三角形。
2.相似三角形对应边的比叫做相似比。
3、相似比为1的两个三角形为全等三角形。
4、能正确识别相似三角形的对应边和对应角,并能灵活解决相关问题。
注:相似比中,各个比的前项为同一个三角形的边,各个比的后项为另一个三角形的边。作业P73、1、2、3,
练习册P28,
预习P73-75。小结
的两个多边形相似。2019/3/153问题 1985年著名建筑大师贝聿铭在设计巴黎卢浮宫前玻璃金字塔时需要先设计一个小模型,模型侧面三角形与实际建筑侧面三角形形状相同,但大小不等 . 这两个三角形是什么关系?2019/3/154观察与思考 观察下图,△ABC与△AFE的三条边以及三个角之间是什么关系? 对应边成比例,对应角相等2019/3/155定义:对应边成比例,对应角相等的三角形叫做相似三角形。如图△ABC相似于△A`B`C`
记作:△ABC∽△A`B`C` 注: 在记两个三角形相似时,通常把对应顶点的字母写在对应的位置上,这样比较容易找出对应元素。相等的角的顶点∽∽∽∽2019/3/156则∠A= ∠A`, ∠ B=∠B`, ∠ C=∠ C` 相似三角形对应边的比叫做相似比。
注:相似比中,各个比的前项为同一个三角形的边,各个比的后项为另一个三角形的边。 若 △ABC∽△A`B`C` △A`B`C`和△ABC 的
相似比为 。 K=1时,
△ABC≌△A`B`C`A`B`C`2019/3/157 思考: 如图:△ABC∽ △ACD,其中∠B=∠ACD,请写出它们的对应角的相等关系及对应边的比例式. 解:∠A=∠A,∠B=∠ACD,∠ACB=∠ADC对应角所对的边是对应边,反之对应边所对的角是对应角。ACD23答:2、如图, △ACD与 △ABC的相似比为( )1、 等于哪两条线段的积?2019/3/158判断1.若△ABC∽△A`B`C`,则
AB:BC:AC=A`B`:B`C`:A`C`
2.若△ABC∽△A`B`C`,且B`C`=3, BC=5,则相似比为3:5。
3.全等三角形一定相似。
4.所有的等腰三角形都相似。
5.所有的等边三角形都相似。
6.所有的直角三角形都相似。√×√√××正确答案: 5:32019/3/159相似比为填空:1.△ABC中,AB=6,BC=4,CA=9,且△ABC∽△A`B`C`,△A`B`C`的最短边的长为8,则最长边的长为( )
2、 △ABC∽△A`B`C`,∠A=400,∠B=1100,则∠C`=( )0。
3、 △ABC∽△A`B`C` ,△ABC的三边长分别是 3、4、5,且 △A`B`C`的最大边长为15,则△A`B`C`的周长为( ), △ABC与△A`B`C`的周长的比为( )。
183036注意 “对应”∠C=相似比为2019/3/1510解:∠A=∠A,
∠ADE=∠B,
∠AED=∠C。
解:∠DAE=∠BAC,
∠D=∠B,
∠E=∠C。关解答ADE2019/3/1511解:∠A=∠A,
∠AED=∠B,
∠ADE=∠C。AED2019/3/1512A选择2019/3/1513B2019/3/15141.相似三角形的定义:对应角相等,对应边成比例的三角形叫做相似三角形。
2.相似三角形对应边的比叫做相似比。
3、相似比为1的两个三角形为全等三角形。
4、能正确识别相似三角形的对应边和对应角,并能灵活解决相关问题。
注:相似比中,各个比的前项为同一个三角形的边,各个比的后项为另一个三角形的边。作业P73、1、2、3,
练习册P28,
预习P73-75。小结
