2023秋学期八年级数学第一学期期中学情评估试题(含答案)
文档属性
| 名称 | 2023秋学期八年级数学第一学期期中学情评估试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 149.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-04 11:07:57 | ||
图片预览




文档简介
2023秋学期八年级数学第一学期期中学情评估试题
一、选择题(本大题共10小题,每小题4分,满分40分)
1.若点P(m,1)在第二象限内,则点Q(-m,0)在( )
A.x轴正半轴上 B.x轴负半轴上
C.y轴正半轴上 D.y轴负半轴上
2.下列函数:(1)y=πx;(2)y=-2x+1;(3)y=;(4)y=2-1-3x;(5)y=x2-1中,一次函数有( )
A.1个 B.2个 C.3个 D.4个
3.已知一次函数y=(k-2)x+5,若y的值随x的值的增大而减小,则k的取值范围是( )
A.k>2 B.k<2
C.0<k<2 D.k<0
4.下列命题中是假命题的是( )
A.一个锐角的补角大于这个角
B.凡能被2整除的数,末位数字必是偶数
C.两条直线被第三条直线所截,同旁内角互补
D.相反数等于它本身的数是0
5.如图,一次函数y=kx+b(k≠0)的图象经过A(2,0),B(0,-2)两点,则关于x的不等式kx+b<0的解集是( )
A.x>2 B.x<2
C.-2<x<2 D.-2≤x≤2
INCLUDEPICTURE"JZ-1.tif" INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-1.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-1.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-1.tif" \* MERGEFORMATINET (第5题) INCLUDEPICTURE"JZ-2.tif" INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-2.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-2.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-2.tif" \* MERGEFORMATINET (第7题)
6.已知在△ABC中,∠A=100°-∠B,则△ABC是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.前三种都有可能
7.如图,△ABC的面积为8,AD为BC边上的中线,E为AD上任意一点,连接BE,CE,图中阴影部分的面积为( )
A.2 B.3 C.4 D.5
8.等腰三角形的周长是18 cm,其中一边长为4 cm,其他两边长分别为( )
A.4 cm,10 cm B.7 cm,7 cm
C.4 cm,10 cm或7 cm,7 cm D.无法确定
9.小明把两个直角三角尺按如图所示的方式摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于( )
A.180° B.210°
C.360° D.270°
INCLUDEPICTURE"JZ-3.tif" INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-3.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-3.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-3.tif" \* MERGEFORMATINET (第9题) INCLUDEPICTURE"JZ-4.tif" INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-4.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-4.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-4.tif" \* MERGEFORMATINET (第10题)
10.甲、乙两车从A地出发,匀速驶向B地.甲车以80 km/h的速度行驶1 h后,乙车才沿相同路线行驶.乙车先到达B地并停留1 h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶的时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度是120 km/h;②m=160;③点H的坐标是(7,80);④n=7.5.其中说法正确的有( )
A.4个 B.3个 C.2个 D.1个
二、填空题(本大题共4小题,每小题5分,满分20分)
11.函数y=中自变量x的取值范围是___________________________________________________.
12.在△ABC中,∠A=∠B=∠C,则∠B=________度.
13.已知y-2与x成正比例,且当x=-1时y=5,则y与x的函数关系式是____________.
14.已知点P(3m-6,m+1).
(1)若点P在y轴上,则点P的坐标为________;
(2)若点P的横坐标比纵坐标小5,则点P在第______象限.
三、(本大题共2小题,每小题8分,满分16分)
15.如图是某单位的部分平面示意图,已知大门的坐标为(-3,0),花坛的坐标为(0,-1).
(1)根据上述条件建立平面直角坐标系;
(2)建筑物A的坐标为(3,1),请在图中标出点A的位置.
INCLUDEPICTURE"F25.tif" INCLUDEPICTURE "D:\\课件\\八数HK安徽\\F25.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\F25.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\F25.tif" \* MERGEFORMATINET
(第15题)
16.已知等腰三角形的周长是20 cm,设腰长为x cm,底边长为y cm.
(1)求y关于x的函数表达式,并求出自变量x的取值范围;
(2)在如图所示的平面直角坐标系中画出函数图象.
INCLUDEPICTURE"TJ8.tif" INCLUDEPICTURE "D:\\课件\\八数HK安徽\\TJ8.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\TJ8.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\TJ8.tif" \* MERGEFORMATINET
(第16题)
四、(本大题共2小题,每小题8分,满分16分)
17.已知一次函数y=(m+3)x+m-4.
(1)m为何值时,该一次函数的图象经过原点?
(2)将该一次函数的图象向下平移3个单位后得到的函数图象经过点(2,5),求平移后的图象对应的函数表达式.
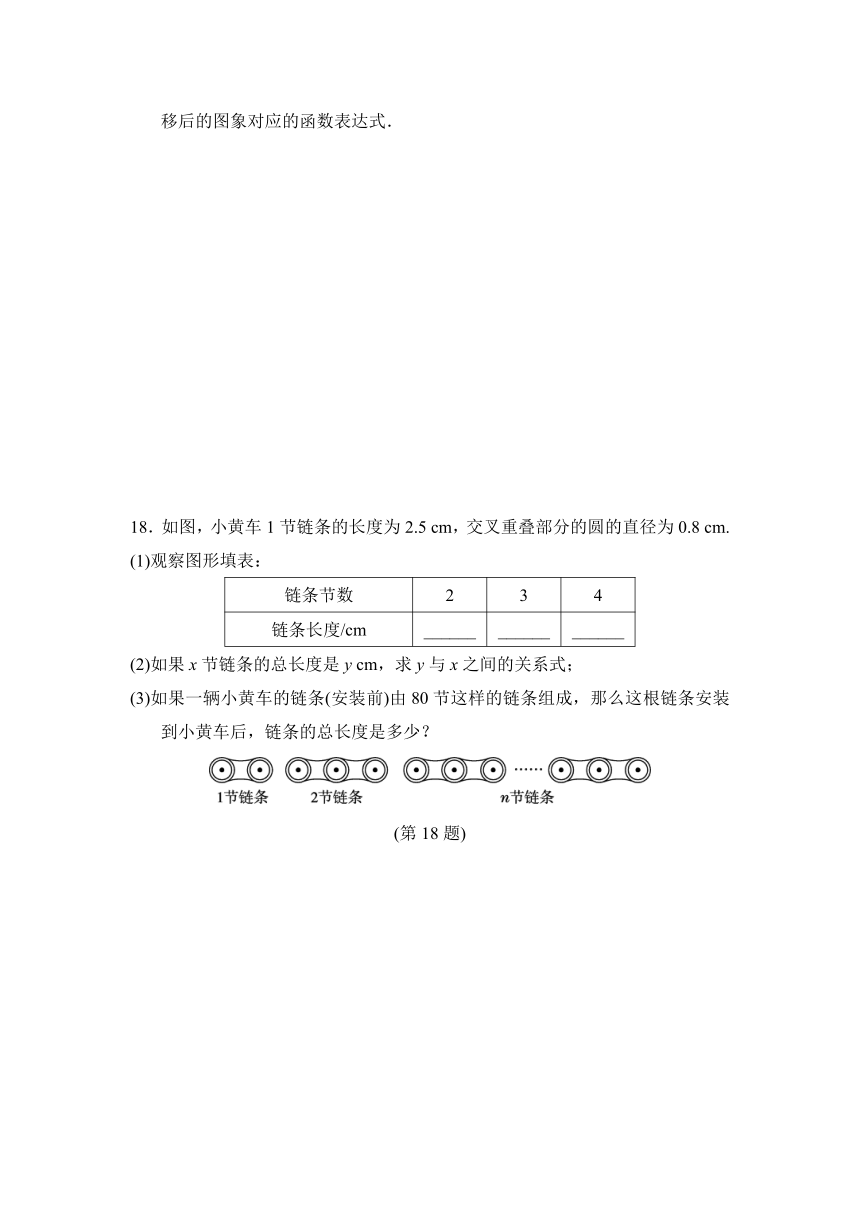
18.如图,小黄车1节链条的长度为2.5 cm,交叉重叠部分的圆的直径为0.8 cm.
(1)观察图形填表:
链条节数 2 3 4
链条长度/cm ______ ______ ______
(2)如果x节链条的总长度是y cm,求y与x之间的关系式;
(3)如果一辆小黄车的链条(安装前)由80节这样的链条组成,那么这根链条安装到小黄车后,链条的总长度是多少?
INCLUDEPICTURE"JZ-5.tif" INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-5.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-5.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-5.tif" \* MERGEFORMATINET
(第18题)
五、(本大题共2小题,每小题10分,满分20分)
19.(1) 完成下面的推理说明:
已知: 如图,BE∥CF,BE,CF分别平分∠ABC和∠BCD.
求证:AB∥CD.
证明:∵BE,CF分别平分∠ABC和∠BCD(已知) ,
∴∠1=∠______,∠2=∠______(____________).
INCLUDEPICTURE"JZ-6.tif" INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-6.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-6.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-6.tif" \* MERGEFORMATINET
(第19题)
∵BE∥CF(____________),
∴∠1=∠2(______________________).
∴∠ABC=∠BCD(____________),
∴∠ABC=∠BCD(等式的性质),
∴AB∥CD(______________________).
(2) 说出 (1) 的推理中运用了哪两个互逆的真命题.
20.如图,已知在△ABC中,∠A∶∠B∶∠ACB=2∶3∶4,CD是∠ACB的平分线,求∠A和∠CDB的度数.
INCLUDEPICTURE"JZ-7.tif" INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-7.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-7.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-7.tif" \* MERGEFORMATINET
(第20题)
六、(本题满分12分)
21.新春佳节来临,某公司组织10辆汽车装运苹果、芦柑、香梨三种水果共60 t去外地销售,要求10辆汽车全部装满,每辆汽车只能装运同一种水果,且装运每种水果的车辆都不少于2辆,根据下表提供的信息,解答以下问题:
苹果 芦柑 香梨
每辆汽车载货量/t 7 6 5
每辆汽车水果获利/元 2 500 3 000 2 000
(1)设装运苹果的车辆为x辆,装运芦柑的车辆为y辆,求y与x之间的函数关系式,并直接写出x的取值范围.
(2)设销售获得的利润为w元,那么怎样安排车辆能使此次销售获利最大?并求出w的最大值.
七、(本题满分12分)
22.如图,已知直线AB:y=kx+b经过点B(1,4),且与直线y=-x-11平行,与直线y=2x-4交于点C.
(1)求直线AB的表达式并求出点C的坐标;
(2)直接写出关于x的不等式0<2x-4<kx+b的解集;
(3)现有一点P在直线AB上,过点P作PQ∥y轴交直线y=2x-4于点Q,若点C到线段PQ的距离为1,求点P的坐标并直接写出线段PQ的长.
INCLUDEPICTURE"JZ-8.tif" INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-8.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-8.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-8.tif" \* MERGEFORMATINET
(第22题)
八、(本题满分14分)
23.一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地,两车同时出发,设行驶的时间为x h,两车之间的距离为y km,图中的折线表示y与x之间的函数关系.根据图象解决以下问题:
(1)求慢车和快车的速度;
(2)解释图中点C的实际意义并求出点C的坐标;
(3)求当x为多少时,两车之间的距离为500 km.
INCLUDEPICTURE"S-31.tif" INCLUDEPICTURE "D:\\课件\\八数HK安徽\\S-31.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\S-31.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\S-31.tif" \* MERGEFORMATINET
(第23题)
答案
一、1.A 2.C 3.B 4.C 5.B 6.D 7.C 8.B
9.B 10.B
二、11.x≥-2且x≠1 12.60 13.y=-3x+2
14.(1)(0,3) (2)二
点拨:(1)利用y轴上点的坐标特征得到3m-6=0,然后解方程求出m即可得到点P的坐标;
(2)利用点P的横坐标比纵坐标小5,得到3m-6+5=m+1,然后解方程求出m即可得到点P的坐标,从而可判断点P所在的象限.
三、15.解:(1)建立的平面直角坐标系如图所示.
INCLUDEPICTURE"F66.tif" INCLUDEPICTURE "D:\\课件\\八数HK安徽\\F66.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\F66.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\F66.tif" \* MERGEFORMATINET (第15题)
(2)点A的位置如图所示.
16.解:(1)根据题意,得2x+y=20,所以y=20-2x.
由x+x>20-2x,得x>5,由20-2x>0,得x<10,故自变量x的取值范围为5<x<10.
(2)如图.
INCLUDEPICTURE"TJ14.tif" INCLUDEPICTURE "D:\\课件\\八数HK安徽\\TJ14.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\TJ14.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\TJ14.tif" \* MERGEFORMATINET (第16题)
四、17.解:(1)因为一次函数y=(m+3)x+m-4的图象经过原点,所以m-4=0,m+3≠0,解得m=4.
(2)一次函数y=(m+3)x+m-4的图象向下平移3个单位后得到的图象对应的函数表达式为
y=(m+3)x+m-7,
因为该图象经过点(2,5),所以5=2(m+3)+m-7,
解得m=2,所以平移后的图象对应的函数表达式为
y=5x-5.
18.解:(1)4.2;5.9;7.6
(2)y=2.5x-0.8(x-1)=1.7x+0.8.
(3)因为小黄车上的链条为环形,在展直的基础上还要缩短0.8 cm,故链条的总长度为1.7×80=136(cm).
五、19.解: (1)ABC;BCD;角平分线的定义;已知;两直线平行, 内错角相等;等量代换;内错角相等, 两直线平行
(2) 两个互逆的真命题为两直线平行, 内错角相等和内错角相等, 两直线平行 .
20.解:∵在△ABC中,∠A∶∠B∶∠ACB=2∶3∶4 ,
∠A+∠ACB+∠B=180°,
∴∠A=×180°=40°,∠ACB=×180°=80°.
∵CD是∠ACB的平分线,
∴∠ACD=∠ACB=40°,
∴∠CDB=∠A+∠ACD=40°+40°=80°.
六、21.解:(1)由题意得7x+6y+5(10-x-y)=60,
所以y=-2x+10(2≤x≤4,且x为正整数).
(2)w=2 500x+3 000(-2x+10)+2 000[10-x-(-2x+10)],即w=-1 500x+30 000,
当x=2时,w有最大值27 000,此时-2×2+10=6(辆),10-2-6=2(辆).
所以安排装运苹果的车辆为2辆,装运芦柑的车辆为6辆,装运香梨的车辆为2辆时,能使此次销售获利最大,w的最大值为27 000.
七、22.解:(1)∵直线AB:y=kx+b与直线y=-x-11平行,
∴k=-1.
∵直线AB经过点B(1,4),
∴-1+b=4,解得b=5,
∴直线AB的表达式为y=-x+5.
由直线AB与直线y=2x-4交于点C,
得解得
∴点C的坐标为(3,2).
(2)解集是2<x<3.
(3)∵点C(3,2)到线段PQ的距离为1,PQ∥y轴,
∴点P的横坐标为2或4.
∵点P在直线AB上,
∴x=2时,y=-2+5=3;x=4时,y=-4+5=1,
∴点P的坐标为(2,3)或(4,1).
线段PQ的长为3.
八、23.解:(1)设慢车的速度为a km/h,快车的速度为b km/h,
根据题意,得解得
即慢车的速度为80 km/h,快车的速度为120 km/h.
(2)点C的实际意义是快车到达乙地.
因为快车走完全程所需时间为720÷120=6(h),
所以点C的横坐标为6,纵坐标为(80+120)×(6-3.6)=480,即点C的坐标为(6,480).
(3)由题意可知两车行驶的过程中有两次两车之间的距离为500 km.
相遇前:(80+120)x=720-500,解得x=1.1.
相遇后:因为点C(6,480),
所以慢车再行驶20 km后两车之间的距离为500 km.
因为慢车行驶20 km需要的时间是=0.25(h),
所以x=6+0.25=6.25.
故当x=1.1或x=6.25时,两车之间的距离为500 km.
一、选择题(本大题共10小题,每小题4分,满分40分)
1.若点P(m,1)在第二象限内,则点Q(-m,0)在( )
A.x轴正半轴上 B.x轴负半轴上
C.y轴正半轴上 D.y轴负半轴上
2.下列函数:(1)y=πx;(2)y=-2x+1;(3)y=;(4)y=2-1-3x;(5)y=x2-1中,一次函数有( )
A.1个 B.2个 C.3个 D.4个
3.已知一次函数y=(k-2)x+5,若y的值随x的值的增大而减小,则k的取值范围是( )
A.k>2 B.k<2
C.0<k<2 D.k<0
4.下列命题中是假命题的是( )
A.一个锐角的补角大于这个角
B.凡能被2整除的数,末位数字必是偶数
C.两条直线被第三条直线所截,同旁内角互补
D.相反数等于它本身的数是0
5.如图,一次函数y=kx+b(k≠0)的图象经过A(2,0),B(0,-2)两点,则关于x的不等式kx+b<0的解集是( )
A.x>2 B.x<2
C.-2<x<2 D.-2≤x≤2
INCLUDEPICTURE"JZ-1.tif" INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-1.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-1.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-1.tif" \* MERGEFORMATINET (第5题) INCLUDEPICTURE"JZ-2.tif" INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-2.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-2.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-2.tif" \* MERGEFORMATINET (第7题)
6.已知在△ABC中,∠A=100°-∠B,则△ABC是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.前三种都有可能
7.如图,△ABC的面积为8,AD为BC边上的中线,E为AD上任意一点,连接BE,CE,图中阴影部分的面积为( )
A.2 B.3 C.4 D.5
8.等腰三角形的周长是18 cm,其中一边长为4 cm,其他两边长分别为( )
A.4 cm,10 cm B.7 cm,7 cm
C.4 cm,10 cm或7 cm,7 cm D.无法确定
9.小明把两个直角三角尺按如图所示的方式摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于( )
A.180° B.210°
C.360° D.270°
INCLUDEPICTURE"JZ-3.tif" INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-3.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-3.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-3.tif" \* MERGEFORMATINET (第9题) INCLUDEPICTURE"JZ-4.tif" INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-4.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-4.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-4.tif" \* MERGEFORMATINET (第10题)
10.甲、乙两车从A地出发,匀速驶向B地.甲车以80 km/h的速度行驶1 h后,乙车才沿相同路线行驶.乙车先到达B地并停留1 h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶的时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度是120 km/h;②m=160;③点H的坐标是(7,80);④n=7.5.其中说法正确的有( )
A.4个 B.3个 C.2个 D.1个
二、填空题(本大题共4小题,每小题5分,满分20分)
11.函数y=中自变量x的取值范围是___________________________________________________.
12.在△ABC中,∠A=∠B=∠C,则∠B=________度.
13.已知y-2与x成正比例,且当x=-1时y=5,则y与x的函数关系式是____________.
14.已知点P(3m-6,m+1).
(1)若点P在y轴上,则点P的坐标为________;
(2)若点P的横坐标比纵坐标小5,则点P在第______象限.
三、(本大题共2小题,每小题8分,满分16分)
15.如图是某单位的部分平面示意图,已知大门的坐标为(-3,0),花坛的坐标为(0,-1).
(1)根据上述条件建立平面直角坐标系;
(2)建筑物A的坐标为(3,1),请在图中标出点A的位置.
INCLUDEPICTURE"F25.tif" INCLUDEPICTURE "D:\\课件\\八数HK安徽\\F25.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\F25.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\F25.tif" \* MERGEFORMATINET
(第15题)
16.已知等腰三角形的周长是20 cm,设腰长为x cm,底边长为y cm.
(1)求y关于x的函数表达式,并求出自变量x的取值范围;
(2)在如图所示的平面直角坐标系中画出函数图象.
INCLUDEPICTURE"TJ8.tif" INCLUDEPICTURE "D:\\课件\\八数HK安徽\\TJ8.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\TJ8.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\TJ8.tif" \* MERGEFORMATINET
(第16题)
四、(本大题共2小题,每小题8分,满分16分)
17.已知一次函数y=(m+3)x+m-4.
(1)m为何值时,该一次函数的图象经过原点?
(2)将该一次函数的图象向下平移3个单位后得到的函数图象经过点(2,5),求平移后的图象对应的函数表达式.
18.如图,小黄车1节链条的长度为2.5 cm,交叉重叠部分的圆的直径为0.8 cm.
(1)观察图形填表:
链条节数 2 3 4
链条长度/cm ______ ______ ______
(2)如果x节链条的总长度是y cm,求y与x之间的关系式;
(3)如果一辆小黄车的链条(安装前)由80节这样的链条组成,那么这根链条安装到小黄车后,链条的总长度是多少?
INCLUDEPICTURE"JZ-5.tif" INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-5.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-5.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-5.tif" \* MERGEFORMATINET
(第18题)
五、(本大题共2小题,每小题10分,满分20分)
19.(1) 完成下面的推理说明:
已知: 如图,BE∥CF,BE,CF分别平分∠ABC和∠BCD.
求证:AB∥CD.
证明:∵BE,CF分别平分∠ABC和∠BCD(已知) ,
∴∠1=∠______,∠2=∠______(____________).
INCLUDEPICTURE"JZ-6.tif" INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-6.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-6.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-6.tif" \* MERGEFORMATINET
(第19题)
∵BE∥CF(____________),
∴∠1=∠2(______________________).
∴∠ABC=∠BCD(____________),
∴∠ABC=∠BCD(等式的性质),
∴AB∥CD(______________________).
(2) 说出 (1) 的推理中运用了哪两个互逆的真命题.
20.如图,已知在△ABC中,∠A∶∠B∶∠ACB=2∶3∶4,CD是∠ACB的平分线,求∠A和∠CDB的度数.
INCLUDEPICTURE"JZ-7.tif" INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-7.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-7.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-7.tif" \* MERGEFORMATINET
(第20题)
六、(本题满分12分)
21.新春佳节来临,某公司组织10辆汽车装运苹果、芦柑、香梨三种水果共60 t去外地销售,要求10辆汽车全部装满,每辆汽车只能装运同一种水果,且装运每种水果的车辆都不少于2辆,根据下表提供的信息,解答以下问题:
苹果 芦柑 香梨
每辆汽车载货量/t 7 6 5
每辆汽车水果获利/元 2 500 3 000 2 000
(1)设装运苹果的车辆为x辆,装运芦柑的车辆为y辆,求y与x之间的函数关系式,并直接写出x的取值范围.
(2)设销售获得的利润为w元,那么怎样安排车辆能使此次销售获利最大?并求出w的最大值.
七、(本题满分12分)
22.如图,已知直线AB:y=kx+b经过点B(1,4),且与直线y=-x-11平行,与直线y=2x-4交于点C.
(1)求直线AB的表达式并求出点C的坐标;
(2)直接写出关于x的不等式0<2x-4<kx+b的解集;
(3)现有一点P在直线AB上,过点P作PQ∥y轴交直线y=2x-4于点Q,若点C到线段PQ的距离为1,求点P的坐标并直接写出线段PQ的长.
INCLUDEPICTURE"JZ-8.tif" INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-8.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-8.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\JZ-8.tif" \* MERGEFORMATINET
(第22题)
八、(本题满分14分)
23.一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地,两车同时出发,设行驶的时间为x h,两车之间的距离为y km,图中的折线表示y与x之间的函数关系.根据图象解决以下问题:
(1)求慢车和快车的速度;
(2)解释图中点C的实际意义并求出点C的坐标;
(3)求当x为多少时,两车之间的距离为500 km.
INCLUDEPICTURE"S-31.tif" INCLUDEPICTURE "D:\\课件\\八数HK安徽\\S-31.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\S-31.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\S-31.tif" \* MERGEFORMATINET
(第23题)
答案
一、1.A 2.C 3.B 4.C 5.B 6.D 7.C 8.B
9.B 10.B
二、11.x≥-2且x≠1 12.60 13.y=-3x+2
14.(1)(0,3) (2)二
点拨:(1)利用y轴上点的坐标特征得到3m-6=0,然后解方程求出m即可得到点P的坐标;
(2)利用点P的横坐标比纵坐标小5,得到3m-6+5=m+1,然后解方程求出m即可得到点P的坐标,从而可判断点P所在的象限.
三、15.解:(1)建立的平面直角坐标系如图所示.
INCLUDEPICTURE"F66.tif" INCLUDEPICTURE "D:\\课件\\八数HK安徽\\F66.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\F66.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\F66.tif" \* MERGEFORMATINET (第15题)
(2)点A的位置如图所示.
16.解:(1)根据题意,得2x+y=20,所以y=20-2x.
由x+x>20-2x,得x>5,由20-2x>0,得x<10,故自变量x的取值范围为5<x<10.
(2)如图.
INCLUDEPICTURE"TJ14.tif" INCLUDEPICTURE "D:\\课件\\八数HK安徽\\TJ14.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\TJ14.tif" \* MERGEFORMATINET INCLUDEPICTURE "D:\\课件\\八数HK安徽\\TJ14.tif" \* MERGEFORMATINET (第16题)
四、17.解:(1)因为一次函数y=(m+3)x+m-4的图象经过原点,所以m-4=0,m+3≠0,解得m=4.
(2)一次函数y=(m+3)x+m-4的图象向下平移3个单位后得到的图象对应的函数表达式为
y=(m+3)x+m-7,
因为该图象经过点(2,5),所以5=2(m+3)+m-7,
解得m=2,所以平移后的图象对应的函数表达式为
y=5x-5.
18.解:(1)4.2;5.9;7.6
(2)y=2.5x-0.8(x-1)=1.7x+0.8.
(3)因为小黄车上的链条为环形,在展直的基础上还要缩短0.8 cm,故链条的总长度为1.7×80=136(cm).
五、19.解: (1)ABC;BCD;角平分线的定义;已知;两直线平行, 内错角相等;等量代换;内错角相等, 两直线平行
(2) 两个互逆的真命题为两直线平行, 内错角相等和内错角相等, 两直线平行 .
20.解:∵在△ABC中,∠A∶∠B∶∠ACB=2∶3∶4 ,
∠A+∠ACB+∠B=180°,
∴∠A=×180°=40°,∠ACB=×180°=80°.
∵CD是∠ACB的平分线,
∴∠ACD=∠ACB=40°,
∴∠CDB=∠A+∠ACD=40°+40°=80°.
六、21.解:(1)由题意得7x+6y+5(10-x-y)=60,
所以y=-2x+10(2≤x≤4,且x为正整数).
(2)w=2 500x+3 000(-2x+10)+2 000[10-x-(-2x+10)],即w=-1 500x+30 000,
当x=2时,w有最大值27 000,此时-2×2+10=6(辆),10-2-6=2(辆).
所以安排装运苹果的车辆为2辆,装运芦柑的车辆为6辆,装运香梨的车辆为2辆时,能使此次销售获利最大,w的最大值为27 000.
七、22.解:(1)∵直线AB:y=kx+b与直线y=-x-11平行,
∴k=-1.
∵直线AB经过点B(1,4),
∴-1+b=4,解得b=5,
∴直线AB的表达式为y=-x+5.
由直线AB与直线y=2x-4交于点C,
得解得
∴点C的坐标为(3,2).
(2)解集是2<x<3.
(3)∵点C(3,2)到线段PQ的距离为1,PQ∥y轴,
∴点P的横坐标为2或4.
∵点P在直线AB上,
∴x=2时,y=-2+5=3;x=4时,y=-4+5=1,
∴点P的坐标为(2,3)或(4,1).
线段PQ的长为3.
八、23.解:(1)设慢车的速度为a km/h,快车的速度为b km/h,
根据题意,得解得
即慢车的速度为80 km/h,快车的速度为120 km/h.
(2)点C的实际意义是快车到达乙地.
因为快车走完全程所需时间为720÷120=6(h),
所以点C的横坐标为6,纵坐标为(80+120)×(6-3.6)=480,即点C的坐标为(6,480).
(3)由题意可知两车行驶的过程中有两次两车之间的距离为500 km.
相遇前:(80+120)x=720-500,解得x=1.1.
相遇后:因为点C(6,480),
所以慢车再行驶20 km后两车之间的距离为500 km.
因为慢车行驶20 km需要的时间是=0.25(h),
所以x=6+0.25=6.25.
故当x=1.1或x=6.25时,两车之间的距离为500 km.
同课章节目录
