相似三角形性质的应用[下学期]
图片预览








文档简介
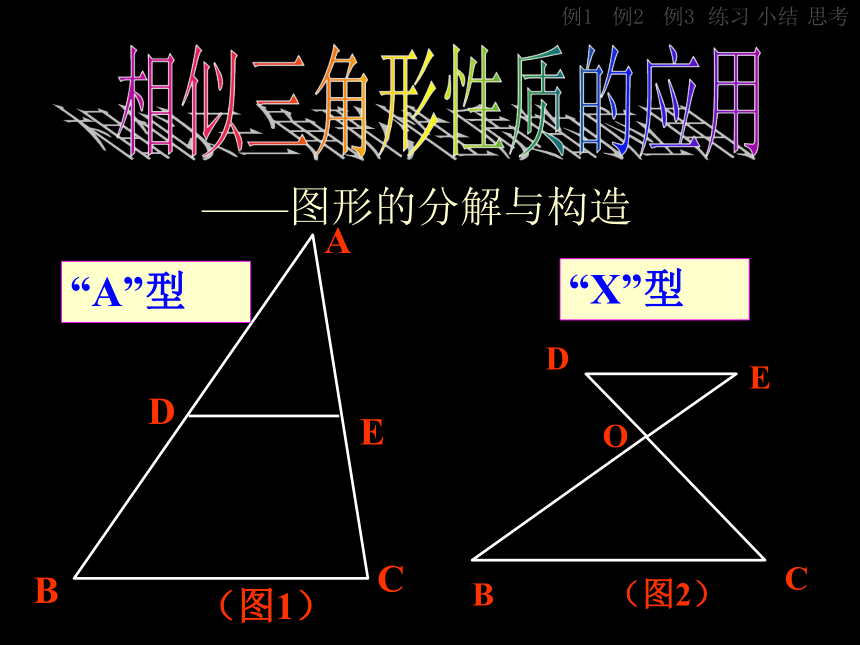
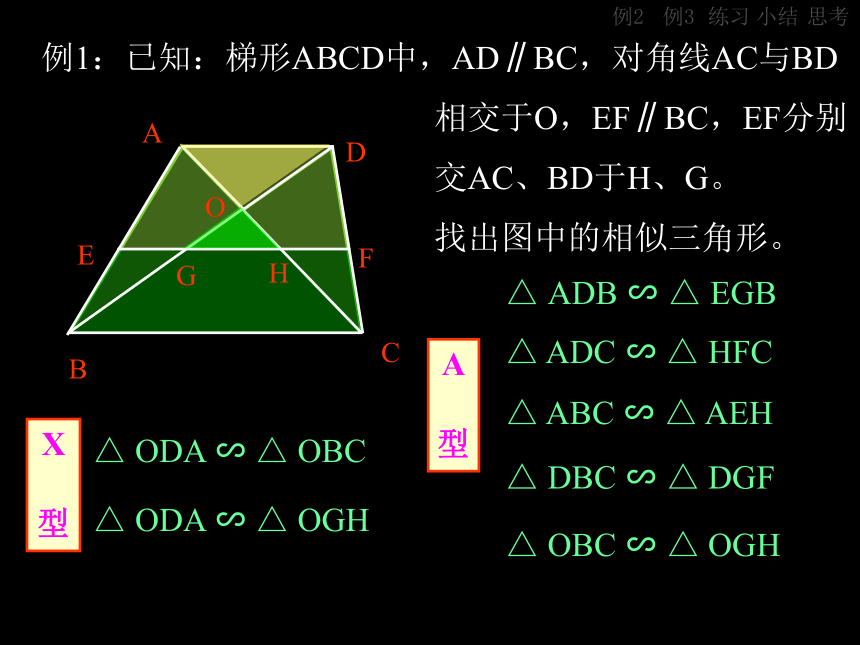
课件37张PPT。相似三角形性质的应用——图形的分解与构造“A”型 “X”型 小结例1例2例3练习思考 例1:已知:梯形ABCD中,AD∥BC,对角线AC与BD
相交于O,EF∥BC,EF分别
交AC、BD于H、G。
找出图中的相似三角形。小结例2例3练习思考 例1:已知:梯形ABCD中,AD∥BC,对角线AC与BD
相交于O,EF∥BC,EF分别
交AC、BD于H、G。
找出图中的相似三角形。△ ADB ∽ △ EGB小结例2例3练习思考 例1:已知:梯形ABCD中,AD∥BC,对角线AC与BD
相交于O,EF∥BC,EF分别
交AC、BD于H、G。
找出图中的相似三角形。△ ADC ∽ △ HFC小结例2例3练习思考 例1:已知:梯形ABCD中,AD∥BC,对角线AC与BD
相交于O,EF∥BC,EF分别
交AC、BD于H、G。
找出图中的相似三角形。△ ABC ∽ △ AEH小结例2例3练习思考 例1:已知:梯形ABCD中,AD∥BC,对角线AC与BD
相交于O,EF∥BC,EF分别
交AC、BD于H、G。
找出图中的相似三角形。△ DBC ∽ △ DGF小结例2例3练习思考 例1:已知:梯形ABCD中,AD∥BC,对角线AC与BD
相交于O,EF∥BC,EF分别
交AC、BD于H、G。
找出图中的相似三角形。△ OBC ∽ △ OGH小结例2例3练习思考 例1:已知:梯形ABCD中,AD∥BC,对角线AC与BD
相交于O,EF∥BC,EF分别
交AC、BD于H、G。
找出图中的相似三角形。△ ODA ∽ △ OBC小结例2例3练习思考 例1:已知:梯形ABCD中,AD∥BC,对角线AC与BD
相交于O,EF∥BC,EF分别
交AC、BD于H、G。
找出图中的相似三角形。△ ODA ∽ △ OGH小结例2例3练习思考△ ADB ∽ △ EGB△ ADC ∽ △ HFC△ ABC ∽ △ AEH△ DBC ∽ △ DGF△ OBC ∽ △ OGH△ ODA ∽ △ OBC△ ODA ∽ △ OGHA
型X
型 例1:已知:梯形ABCD中,AD∥BC,对角线AC与BD
相交于O,EF∥BC,EF分别
交AC、BD于H、G。
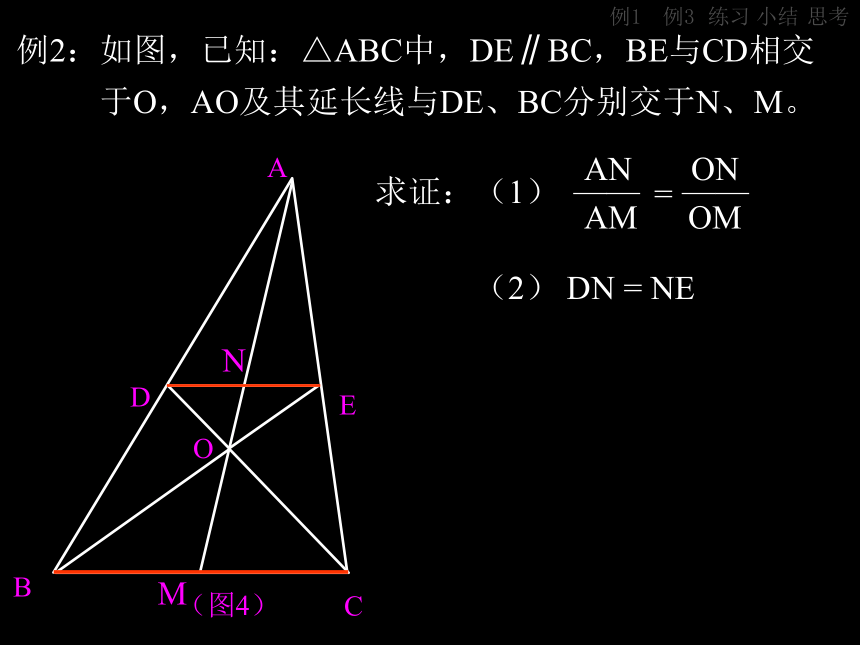
找出图中的相似三角形。小结例2例3练习思考例2:如图,已知:△ABC中,DE∥BC,BE与CD相交
于O,AO及其延长线与DE、BC分别交于N、M。求证:(1)
(2) DN = NEAN ON
AM OM—— ——=NM小结例1例3练习思考例2:如图,已知:△ABC中,DE∥BC,BE与CD相交
于O,AO及其延长线与DE、BC分别交于N、M。(图4)ABCDEO求证:(1)
(2) DN = NEAN ON
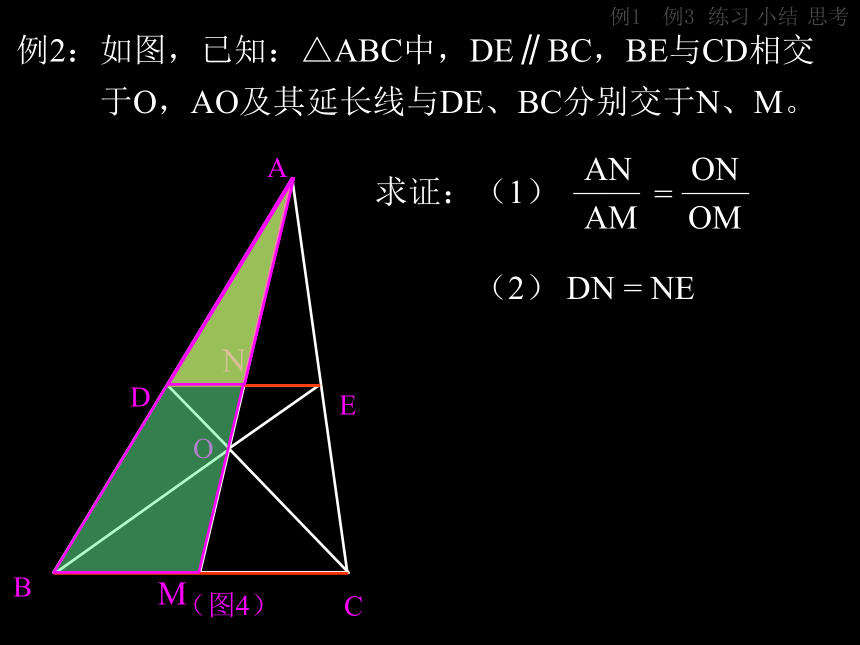
AM OM—— ——=NM小结例3练习思考例1例2:如图,已知:△ABC中,DE∥BC,BE与CD相交
于O,AO及其延长线与DE、BC分别交于N、M。(图4)ABCDEO求证:(1)
(2) DN = NEAN ON
AM OM—— ——=NM小结例3练习思考例1(图4)ABCDEO求证:(1)
(2) DN = NEAN ON
AM OM—— ——=NM小结例3练习思考例2:如图,已知:△ABC中,DE∥BC,BE与CD相交
于O,AO及其延长线与DE、BC分别交于N、M。例1例2:如图,已知:△ABC中,DE∥BC,BE与CD相交
于O,AO及其延长线与DE、BC分别交于N、M。(图4)ABCDEO求证:(1)
(2) DN = NEAN ON
AM OM—— ——=NM小结例3练习思考例1例3:如图,已知:△ABC中,
AD与BE相交于F,且AE=EC,
BD : DC=1 : 2
求:BF : FE小结例1例2练习思考例3:如图,已知:△ABC中,
AD与BE相交于F,且AE=EC,
BD : DC=1 : 2
求:BF : FEK小结练习思考例1例2例3:如图,已知:△ABC中,
AD与BE相交于F,且AE=EC,
BD : DC=1 : 2
求:BF : FEK小结练习思考例1例2例3:如图,已知:△ABC中,
AD与BE相交于F,且AE=EC,
BD : DC=1 : 2
求:BF : FEK小结练习思考例1例2例3:如图,已知:△ABC中,
AD与BE相交于F,且AE=EC,
BD : DC=1 : 2
求:BF : FEK小结练习思考例1例2例3:如图,已知:△ABC中,
AD与BE相交于F,且AE=EC,
BD : DC=1 : 2
求:BF : FEK小结练习思考例1例2例3:如图,已知:△ABC中,
AD与BE相交于F,且AE=EC,
BD : DC=1 : 2
求:BF : FEK小结练习思考例1例2例3:如图,已知:△ABC中,
AD与BE相交于F,且AE=EC,
BD : DC=1 : 2
求:BF : FEK小结练习思考例1例2例3:如图,已知:△ABC中,
AD与BE相交于F,且AE=EC,
BD : DC=1 : 2
求:BF : FEK小结练习思考例1例2例3:如图,已知:△ABC中,
AD与BE相交于F,且AE=EC,
BD : DC=1 : 2
求:BF : FEK小结练习思考例1例2例3:如图,已知:△ABC中,
AD与BE相交于F,且AE=EC,
BD : DC=1 : 2
求:BF : FEABCDEFK小结练习思考例1例2练习:已知:△ABC中,AD、
AG分别交中线BE于F、H,
点D、G是BC的三等分点。
求:BF : FH : HE小结例1例2例3思考练习:已知:△ABC中,AD、
AG分别交中线BE于F、H,
点D、G是BC的三等分点。
求:BF : FH : HE小结思考例1例2例3练习:已知:△ABC中,AD、
AG分别交中线BE于F、H,
点D、G是BC的三等分点。
求:BF : FH : HE小结思考例1例2例3练习:已知:△ABC中,AD、
AG分别交中线BE于F、H,
点D、G是BC的三等分点。
求:BF : FH : HE小结思考例1例2例3练习:已知:△ABC中,AD、
AG分别交中线BE于F、H,
点D、G是BC的三等分点。
求:BF : FH : HE小结思考例1例2例3练习:已知:△ABC中,AD、
AG分别交中线BE于F、H,
点D、G是BC的三等分点。
求:BF : FH : HEAF小结思考例1例2例3AF练习:已知:△ABC中,AD、
AG分别交中线BE于F、H,
点D、G是BC的三等分点。
求:BF : FH : HE小结思考例1例2例3练习:已知:△ABC中,AD、
AG分别交中线BE于F、H,
点D、G是BC的三等分点。
求:BF : FH : HE小结思考例1例2例3 本课,我们研究了如何利用
“图形的分解与构造”的方法来
解决有关相似三角形的问题。1、能在复杂图形中分解出基本图形。2、掌握利用“图形的分解与构造”
的方法构造基本图形。即通过适当
地添加辅助线,以寻求解决问题的
途径。小 结 END例1例2例3练习思考思考题:在矩形ABCD中,
点M是AD的中点,N是BC
的中点,P是CD延长线上
的一点,PM交AC于Q。
求:∠QNM=∠MNPABCNMQOPDEND小结例1例2例3练习
同学们
再见!
相交于O,EF∥BC,EF分别
交AC、BD于H、G。
找出图中的相似三角形。小结例2例3练习思考 例1:已知:梯形ABCD中,AD∥BC,对角线AC与BD
相交于O,EF∥BC,EF分别
交AC、BD于H、G。
找出图中的相似三角形。△ ADB ∽ △ EGB小结例2例3练习思考 例1:已知:梯形ABCD中,AD∥BC,对角线AC与BD
相交于O,EF∥BC,EF分别
交AC、BD于H、G。
找出图中的相似三角形。△ ADC ∽ △ HFC小结例2例3练习思考 例1:已知:梯形ABCD中,AD∥BC,对角线AC与BD
相交于O,EF∥BC,EF分别
交AC、BD于H、G。
找出图中的相似三角形。△ ABC ∽ △ AEH小结例2例3练习思考 例1:已知:梯形ABCD中,AD∥BC,对角线AC与BD
相交于O,EF∥BC,EF分别
交AC、BD于H、G。
找出图中的相似三角形。△ DBC ∽ △ DGF小结例2例3练习思考 例1:已知:梯形ABCD中,AD∥BC,对角线AC与BD
相交于O,EF∥BC,EF分别
交AC、BD于H、G。
找出图中的相似三角形。△ OBC ∽ △ OGH小结例2例3练习思考 例1:已知:梯形ABCD中,AD∥BC,对角线AC与BD
相交于O,EF∥BC,EF分别
交AC、BD于H、G。
找出图中的相似三角形。△ ODA ∽ △ OBC小结例2例3练习思考 例1:已知:梯形ABCD中,AD∥BC,对角线AC与BD
相交于O,EF∥BC,EF分别
交AC、BD于H、G。
找出图中的相似三角形。△ ODA ∽ △ OGH小结例2例3练习思考△ ADB ∽ △ EGB△ ADC ∽ △ HFC△ ABC ∽ △ AEH△ DBC ∽ △ DGF△ OBC ∽ △ OGH△ ODA ∽ △ OBC△ ODA ∽ △ OGHA
型X
型 例1:已知:梯形ABCD中,AD∥BC,对角线AC与BD
相交于O,EF∥BC,EF分别
交AC、BD于H、G。
找出图中的相似三角形。小结例2例3练习思考例2:如图,已知:△ABC中,DE∥BC,BE与CD相交
于O,AO及其延长线与DE、BC分别交于N、M。求证:(1)
(2) DN = NEAN ON
AM OM—— ——=NM小结例1例3练习思考例2:如图,已知:△ABC中,DE∥BC,BE与CD相交
于O,AO及其延长线与DE、BC分别交于N、M。(图4)ABCDEO求证:(1)
(2) DN = NEAN ON
AM OM—— ——=NM小结例3练习思考例1例2:如图,已知:△ABC中,DE∥BC,BE与CD相交
于O,AO及其延长线与DE、BC分别交于N、M。(图4)ABCDEO求证:(1)
(2) DN = NEAN ON
AM OM—— ——=NM小结例3练习思考例1(图4)ABCDEO求证:(1)
(2) DN = NEAN ON
AM OM—— ——=NM小结例3练习思考例2:如图,已知:△ABC中,DE∥BC,BE与CD相交
于O,AO及其延长线与DE、BC分别交于N、M。例1例2:如图,已知:△ABC中,DE∥BC,BE与CD相交
于O,AO及其延长线与DE、BC分别交于N、M。(图4)ABCDEO求证:(1)
(2) DN = NEAN ON
AM OM—— ——=NM小结例3练习思考例1例3:如图,已知:△ABC中,
AD与BE相交于F,且AE=EC,
BD : DC=1 : 2
求:BF : FE小结例1例2练习思考例3:如图,已知:△ABC中,
AD与BE相交于F,且AE=EC,
BD : DC=1 : 2
求:BF : FEK小结练习思考例1例2例3:如图,已知:△ABC中,
AD与BE相交于F,且AE=EC,
BD : DC=1 : 2
求:BF : FEK小结练习思考例1例2例3:如图,已知:△ABC中,
AD与BE相交于F,且AE=EC,
BD : DC=1 : 2
求:BF : FEK小结练习思考例1例2例3:如图,已知:△ABC中,
AD与BE相交于F,且AE=EC,
BD : DC=1 : 2
求:BF : FEK小结练习思考例1例2例3:如图,已知:△ABC中,
AD与BE相交于F,且AE=EC,
BD : DC=1 : 2
求:BF : FEK小结练习思考例1例2例3:如图,已知:△ABC中,
AD与BE相交于F,且AE=EC,
BD : DC=1 : 2
求:BF : FEK小结练习思考例1例2例3:如图,已知:△ABC中,
AD与BE相交于F,且AE=EC,
BD : DC=1 : 2
求:BF : FEK小结练习思考例1例2例3:如图,已知:△ABC中,
AD与BE相交于F,且AE=EC,
BD : DC=1 : 2
求:BF : FEK小结练习思考例1例2例3:如图,已知:△ABC中,
AD与BE相交于F,且AE=EC,
BD : DC=1 : 2
求:BF : FEK小结练习思考例1例2例3:如图,已知:△ABC中,
AD与BE相交于F,且AE=EC,
BD : DC=1 : 2
求:BF : FEABCDEFK小结练习思考例1例2练习:已知:△ABC中,AD、
AG分别交中线BE于F、H,
点D、G是BC的三等分点。
求:BF : FH : HE小结例1例2例3思考练习:已知:△ABC中,AD、
AG分别交中线BE于F、H,
点D、G是BC的三等分点。
求:BF : FH : HE小结思考例1例2例3练习:已知:△ABC中,AD、
AG分别交中线BE于F、H,
点D、G是BC的三等分点。
求:BF : FH : HE小结思考例1例2例3练习:已知:△ABC中,AD、
AG分别交中线BE于F、H,
点D、G是BC的三等分点。
求:BF : FH : HE小结思考例1例2例3练习:已知:△ABC中,AD、
AG分别交中线BE于F、H,
点D、G是BC的三等分点。
求:BF : FH : HE小结思考例1例2例3练习:已知:△ABC中,AD、
AG分别交中线BE于F、H,
点D、G是BC的三等分点。
求:BF : FH : HEAF小结思考例1例2例3AF练习:已知:△ABC中,AD、
AG分别交中线BE于F、H,
点D、G是BC的三等分点。
求:BF : FH : HE小结思考例1例2例3练习:已知:△ABC中,AD、
AG分别交中线BE于F、H,
点D、G是BC的三等分点。
求:BF : FH : HE小结思考例1例2例3 本课,我们研究了如何利用
“图形的分解与构造”的方法来
解决有关相似三角形的问题。1、能在复杂图形中分解出基本图形。2、掌握利用“图形的分解与构造”
的方法构造基本图形。即通过适当
地添加辅助线,以寻求解决问题的
途径。小 结 END例1例2例3练习思考思考题:在矩形ABCD中,
点M是AD的中点,N是BC
的中点,P是CD延长线上
的一点,PM交AC于Q。
求:∠QNM=∠MNPABCNMQOPDEND小结例1例2例3练习
同学们
再见!
