相似三角形应用[下学期]
图片预览






文档简介
课件16张PPT。§18.3(4)相似三角形的应用相似三角形的性质
1、相似三角形对应角相等,对应边成比例。
2、相似三角形对应高线的比,对应中线的比和对应角平分线的比都等于相似比
3、相似三角形面积比等于相似比的平方,周长比等于相似比。
回忆昨天1、两个相似三角形对应中线之比是1:2,则对应角平分线之比也是1:2。 ( )
2、两个相似三角形面积比是1:2,则相似比是1:4。 ( )
3、三角形中位线把三角形的面积分成1:4两部分。 ( )
4、△ABC∽△A′B′C′,相似比为2:3,若△ABC周长为6,则△A′B′C′周长为9。 ( )
温故而知新√ ××√ 判 断:如图:△ADE∽△ABC, 若AD=5,AB=20,DE=3,显然 ∵ △ADE∽△ABC∵ ×3=12
也就是说:在两个相似三角形中,若已知两组对应边中三边的长,利用相似三角形对应边成比例很容易求出第四边的长。你能求出BC的长吗? 据史料记载,希腊数学家、天文学家泰勒斯(Thales,约625—前547)曾利用相似三角形的原理,测出了金字塔的高度。他的方法与是:在金字塔顶部的影子处立一根杆子,借助太阳光线构成两个相似三角形,塔高与杆高之比等于两者影长之比。由此便可算出金字塔的高度。
?
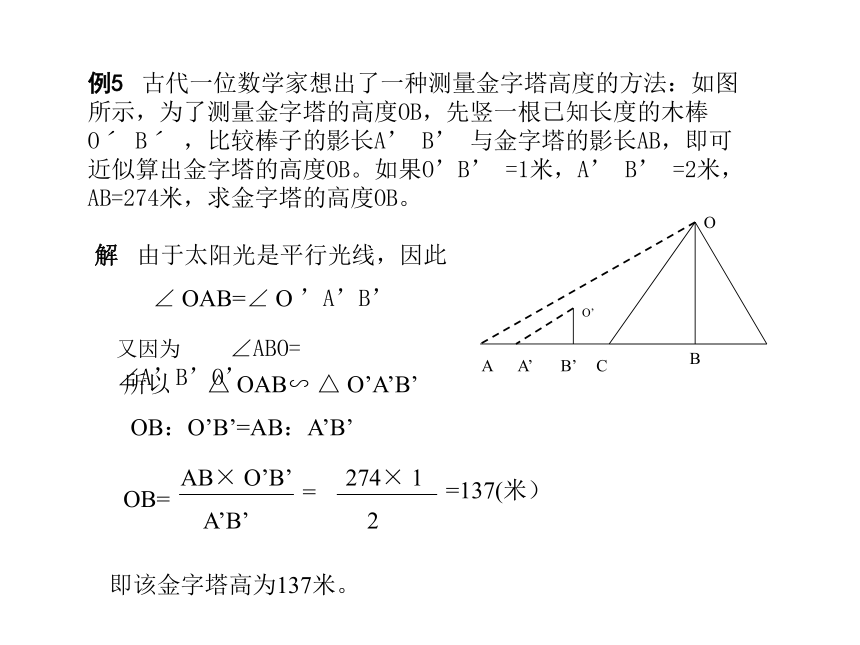
例5 古代一位数学家想出了一种测量金字塔高度的方法:如图所示,为了测量金字塔的高度OB,先竖一根已知长度的木棒Oˊ Bˊ ,比较棒子的影长A’ B’ 与金字塔的影长AB,即可近似算出金字塔的高度OB。如果O’B’ =1米,A’ B’ =2米,AB=274米,求金字塔的高度OB。解 由于太阳光是平行光线,因此∠ OAB=∠ O ’A’B’又因为 ∠ABO= ∠A’B’O’所以 △ OAB∽ △ O’A’B’OB:O’B’=AB:A’B’即该金字塔高为137米。例6 如图所示,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D,此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB。解 因为 ∠ ADB=∠ EDC∠ ABC=∠ ECD=90o所以 △ ABD∽ △ ECD答:两岸间的大致距离为100米。在同一时刻物体的高度与它的影长成正比例,在某
一时刻,有人测得一高为1.8米的竹竿的影长为3米,
某一高楼的影长为60米,那么高楼的高度是多少米?试一试2004年奥运会男子十米气步枪冠军获得者朱启南下图是步枪在瞄准时的俯视图,ABCEDoF80160000.2OE是从眼睛到准星的距离80cm,AB是步枪上的准星宽度2mm,OF是眼睛到正方形靶子的距离160m,求正方形靶子的宽度?OE OF AB CDoB’B(准星)C’C如图,步枪在瞄准时,如果准星(B)偏离准确位置1mm,那么射出去的子弹在10m的距离处就要偏离目标多少cm?(设眼睛离准星的距离为80cm)想一想0.1801080解决实际问题时(如测高、测距)①审题②构建图形③利用相似解决问题谈谈你的收获有一块三角形余料ABC,它的边BC=120cm
高线AD=80cm, (1)若要把它加工成正方形靶子,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,问加工成的正方形靶子的边长为多少cm?ABCD12080X E(80—X)动动脑筋X再见,谢谢指导!
1、相似三角形对应角相等,对应边成比例。
2、相似三角形对应高线的比,对应中线的比和对应角平分线的比都等于相似比
3、相似三角形面积比等于相似比的平方,周长比等于相似比。
回忆昨天1、两个相似三角形对应中线之比是1:2,则对应角平分线之比也是1:2。 ( )
2、两个相似三角形面积比是1:2,则相似比是1:4。 ( )
3、三角形中位线把三角形的面积分成1:4两部分。 ( )
4、△ABC∽△A′B′C′,相似比为2:3,若△ABC周长为6,则△A′B′C′周长为9。 ( )
温故而知新√ ××√ 判 断:如图:△ADE∽△ABC, 若AD=5,AB=20,DE=3,显然 ∵ △ADE∽△ABC∵ ×3=12
也就是说:在两个相似三角形中,若已知两组对应边中三边的长,利用相似三角形对应边成比例很容易求出第四边的长。你能求出BC的长吗? 据史料记载,希腊数学家、天文学家泰勒斯(Thales,约625—前547)曾利用相似三角形的原理,测出了金字塔的高度。他的方法与是:在金字塔顶部的影子处立一根杆子,借助太阳光线构成两个相似三角形,塔高与杆高之比等于两者影长之比。由此便可算出金字塔的高度。
?
例5 古代一位数学家想出了一种测量金字塔高度的方法:如图所示,为了测量金字塔的高度OB,先竖一根已知长度的木棒Oˊ Bˊ ,比较棒子的影长A’ B’ 与金字塔的影长AB,即可近似算出金字塔的高度OB。如果O’B’ =1米,A’ B’ =2米,AB=274米,求金字塔的高度OB。解 由于太阳光是平行光线,因此∠ OAB=∠ O ’A’B’又因为 ∠ABO= ∠A’B’O’所以 △ OAB∽ △ O’A’B’OB:O’B’=AB:A’B’即该金字塔高为137米。例6 如图所示,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D,此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB。解 因为 ∠ ADB=∠ EDC∠ ABC=∠ ECD=90o所以 △ ABD∽ △ ECD答:两岸间的大致距离为100米。在同一时刻物体的高度与它的影长成正比例,在某
一时刻,有人测得一高为1.8米的竹竿的影长为3米,
某一高楼的影长为60米,那么高楼的高度是多少米?试一试2004年奥运会男子十米气步枪冠军获得者朱启南下图是步枪在瞄准时的俯视图,ABCEDoF80160000.2OE是从眼睛到准星的距离80cm,AB是步枪上的准星宽度2mm,OF是眼睛到正方形靶子的距离160m,求正方形靶子的宽度?OE OF AB CDoB’B(准星)C’C如图,步枪在瞄准时,如果准星(B)偏离准确位置1mm,那么射出去的子弹在10m的距离处就要偏离目标多少cm?(设眼睛离准星的距离为80cm)想一想0.1801080解决实际问题时(如测高、测距)①审题②构建图形③利用相似解决问题谈谈你的收获有一块三角形余料ABC,它的边BC=120cm
高线AD=80cm, (1)若要把它加工成正方形靶子,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,问加工成的正方形靶子的边长为多少cm?ABCD12080X E(80—X)动动脑筋X再见,谢谢指导!
