18.3.4相似三角形的应用[下学期]
文档属性
| 名称 | 18.3.4相似三角形的应用[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-04-12 00:00:00 | ||
图片预览






文档简介
课件29张PPT。18.3.4
相似三角形的应用
匡堰中学陈央红回顾:一.相似三角形的识别对应相等对应成比例夹角三边二.相似三角形的性质对应角对应边对应高对应中线对应角平分线等于相似比等于相似比的平方 1 如果两个相似三角形的对应边的比是4:5,小三角形的周长为20,则大三角形的周长为______
2 两个相似三角形的对应角平分线的比是1:4,那么它们的相似比是_______
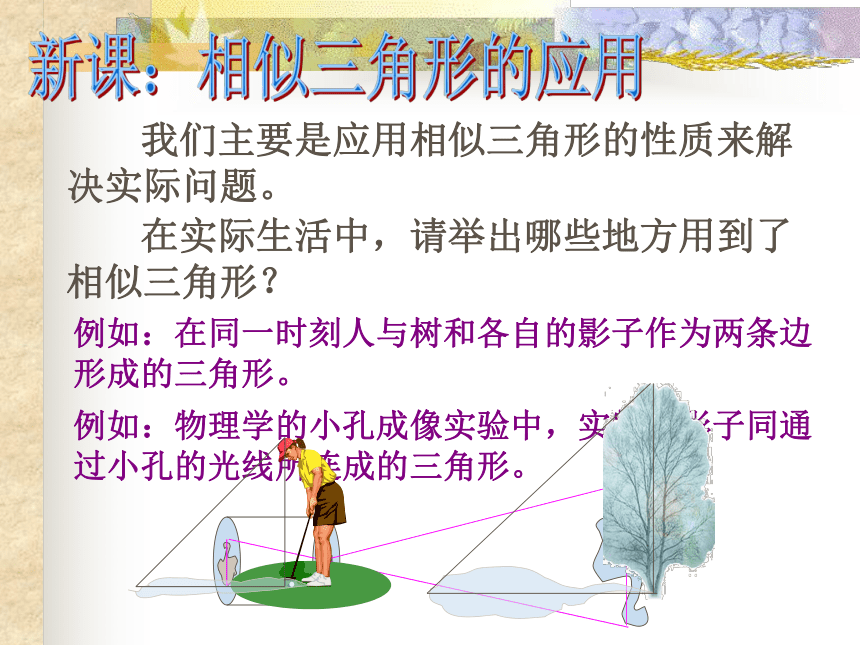
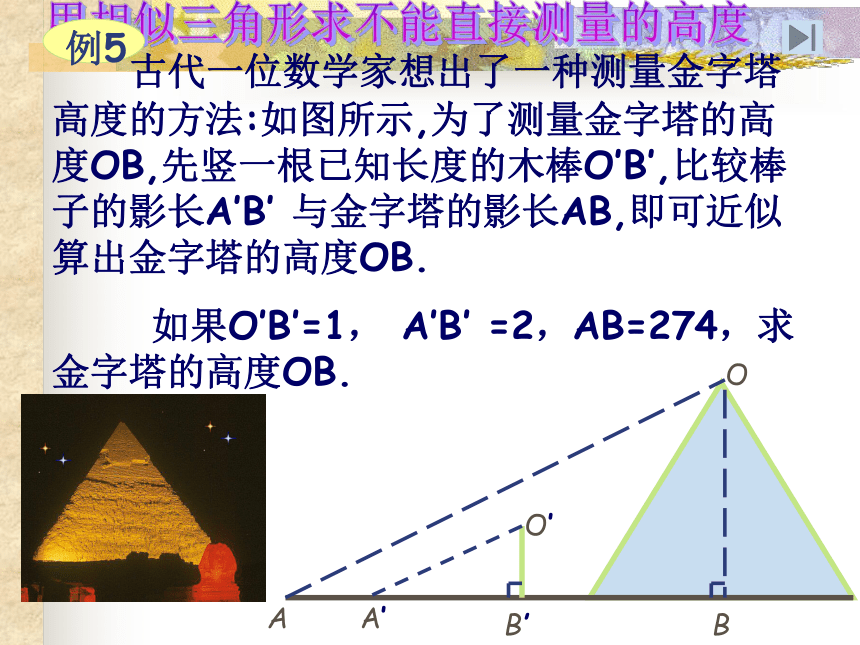
3 若一多边形面积扩大为原来的4倍,且与原多边形相似,则其周长是原来的______倍复习练习251:42新课:相似三角形的应用 我们主要是应用相似三角形的性质来解决实际问题。 在实际生活中,请举出哪些地方用到了相似三角形?例如:在同一时刻人与树和各自的影子作为两条边形成的三角形。例如:物理学的小孔成像实验中,实物与影子同通过小孔的光线所连成的三角形。埃及风景 胡夫金字塔是埃及现存规模最大的金字塔,被喻为“世界古代七大奇观之一”。塔的4个斜面正对东南西北四个方向,塔基呈正方形,每边长约230多米。据考证,为建成大金字塔,共动用了10万人花了20年时间.原高146.59米,但由于经过几千年的风吹雨打,顶端被风化吹蚀.所以高度有所降低 。 小小旅行家:走近金字塔小小考古家: 埃及著名的考古专家穆罕穆德决定重新测量胡夫金字塔的高度.在一个烈日高照的上午.他和儿子小穆罕穆德来到了金字塔脚下,他想考一考年仅14岁的小穆罕穆德.给你一条1米高的木杆,一把皮尺, 你能利用所学知识来测出塔高吗?1米木杆皮尺 用相似三角形求不能直接测量的高度 古代一位数学家想出了一种测量金字塔高度的方法:如图所示,为了测量金字塔的高度OB,先竖一根已知长度的木棒O’B’,比较棒子的影长A’B’ 与金字塔的影长AB,即可近似算出金字塔的高度OB.
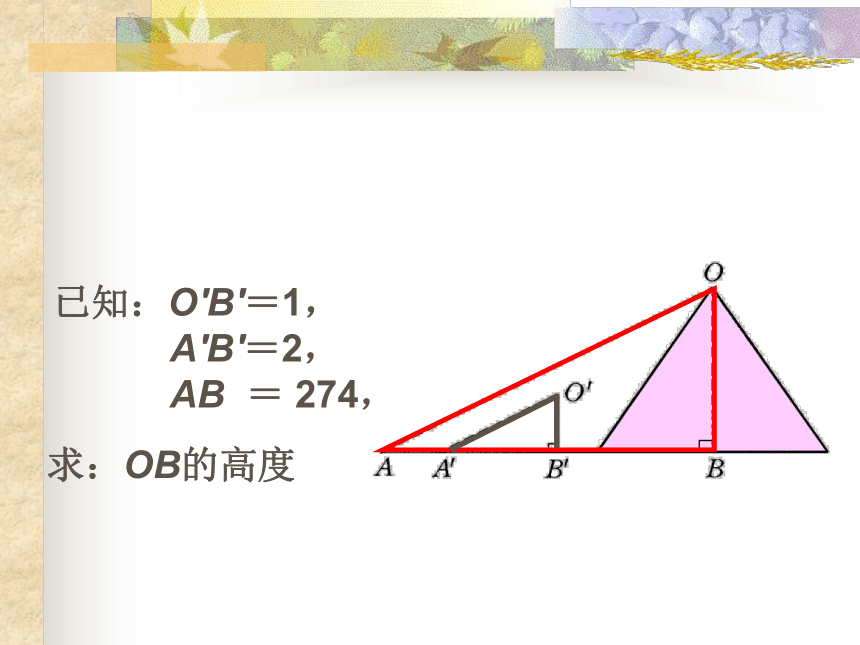
如果O’B’=1, A’B’ =2,AB=274,求金字塔的高度OB.已知:O′B′=1,
A′B′=2,
AB = 274,求:OB的高度 解 由于太阳光是平行光线,
∴ ∠OAB=∠O′A′B′. 又∵ ∠ABO=∠A′B′O′=90°.
∴ △OAB∽△O′A′B′,
?
∴ OB∶O′B′=AB∶A′B′,
?
即该金字塔高为137米.
?
OB= (米), 想一想怎样利用相似三角形的有关知识测量旗杆的高度?怎么办?方法1:利用阳光下的影子.测量数据:身高AC、影长BC、旗杆影长EF.找相似:△ABC∽△DEF.方法1:利用阳光下的影子.怎么办?方法2:利用标杆.HK方法2:利用标杆.测量数据:身高AD、标杆BE、旗杆与标杆
之间距离BC、人与标杆间距离AB.找相似:△AGD∽△BEG. △AGD∽△CFG△DKE∽△DHFKHDK:DH=EK:HF
方法2:利用标杆.测量数据:身高AD、标杆BE、旗杆与标杆之间距离BC、人与标杆间距离AB.找相似找比例怎么办?方法3:利用镜子的反射.方法3:利用镜子的反射.测量数据:身高DE、人与镜子间的距离AE、
旗杆与镜子间距离AC.找相似:△ADE∽△ABC.例6 如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.?此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB.ADCEB解: 因为 ∠ADB=∠EDC, ?
∠ABC=∠ECD=90°, ? 所以 △ABD∽△ECD, ?
答: 两岸间的大致距离为100米. ? 我们还可以在河对岸选定一目标点A,再在河的一边选点D和 E,使DE⊥AD,然后,再选点B,作BC∥DE,与视线EA相交于点C。此时,测得DE , BC, BD, 就可以求两岸间的大致距离AB了。探究:你还能想出别的方法测量河宽吗?为了测量一池塘的宽AB你能利用相似三角形的性质来解决吗?ABBEADC练习2.为了测量一池塘的宽AB,在岸边找到了一点C,使AC⊥AB,在AC上找到一点D,在BC上找到一点E,使DE⊥AC,测出AD=30m,DC=30m,DE =40m,那么你能算出池塘的宽AB吗?ABCDE解:因为 ∠ACB=∠DCE ,所以 △ABC∽△DEC , 答: 池塘的宽大致为80米. ? ∠CAB=∠CDE=90°,ABCDE课堂小结:一 相似三角形的应用主要有如下两个方面
1 测高(不能直接使用皮尺或刻度尺量的)
2 测距(不能直接测量的两点间的距离)测高的方法
测量不能到达顶部的物体的高度,通常用”在同一时刻物高与影长的比例”的原理解决 测距的方法
测量不能到达两点间的距离,常构造相似三角形求解作业P82 习题 6
2. 测出学校的国旗旗杆的高度努力现在,成就未来衷心感谢你们的合作!
相似三角形的应用
匡堰中学陈央红回顾:一.相似三角形的识别对应相等对应成比例夹角三边二.相似三角形的性质对应角对应边对应高对应中线对应角平分线等于相似比等于相似比的平方 1 如果两个相似三角形的对应边的比是4:5,小三角形的周长为20,则大三角形的周长为______
2 两个相似三角形的对应角平分线的比是1:4,那么它们的相似比是_______
3 若一多边形面积扩大为原来的4倍,且与原多边形相似,则其周长是原来的______倍复习练习251:42新课:相似三角形的应用 我们主要是应用相似三角形的性质来解决实际问题。 在实际生活中,请举出哪些地方用到了相似三角形?例如:在同一时刻人与树和各自的影子作为两条边形成的三角形。例如:物理学的小孔成像实验中,实物与影子同通过小孔的光线所连成的三角形。埃及风景 胡夫金字塔是埃及现存规模最大的金字塔,被喻为“世界古代七大奇观之一”。塔的4个斜面正对东南西北四个方向,塔基呈正方形,每边长约230多米。据考证,为建成大金字塔,共动用了10万人花了20年时间.原高146.59米,但由于经过几千年的风吹雨打,顶端被风化吹蚀.所以高度有所降低 。 小小旅行家:走近金字塔小小考古家: 埃及著名的考古专家穆罕穆德决定重新测量胡夫金字塔的高度.在一个烈日高照的上午.他和儿子小穆罕穆德来到了金字塔脚下,他想考一考年仅14岁的小穆罕穆德.给你一条1米高的木杆,一把皮尺, 你能利用所学知识来测出塔高吗?1米木杆皮尺 用相似三角形求不能直接测量的高度 古代一位数学家想出了一种测量金字塔高度的方法:如图所示,为了测量金字塔的高度OB,先竖一根已知长度的木棒O’B’,比较棒子的影长A’B’ 与金字塔的影长AB,即可近似算出金字塔的高度OB.
如果O’B’=1, A’B’ =2,AB=274,求金字塔的高度OB.已知:O′B′=1,
A′B′=2,
AB = 274,求:OB的高度 解 由于太阳光是平行光线,
∴ ∠OAB=∠O′A′B′. 又∵ ∠ABO=∠A′B′O′=90°.
∴ △OAB∽△O′A′B′,
?
∴ OB∶O′B′=AB∶A′B′,
?
即该金字塔高为137米.
?
OB= (米), 想一想怎样利用相似三角形的有关知识测量旗杆的高度?怎么办?方法1:利用阳光下的影子.测量数据:身高AC、影长BC、旗杆影长EF.找相似:△ABC∽△DEF.方法1:利用阳光下的影子.怎么办?方法2:利用标杆.HK方法2:利用标杆.测量数据:身高AD、标杆BE、旗杆与标杆
之间距离BC、人与标杆间距离AB.找相似:△AGD∽△BEG. △AGD∽△CFG△DKE∽△DHFKHDK:DH=EK:HF
方法2:利用标杆.测量数据:身高AD、标杆BE、旗杆与标杆之间距离BC、人与标杆间距离AB.找相似找比例怎么办?方法3:利用镜子的反射.方法3:利用镜子的反射.测量数据:身高DE、人与镜子间的距离AE、
旗杆与镜子间距离AC.找相似:△ADE∽△ABC.例6 如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.?此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB.ADCEB解: 因为 ∠ADB=∠EDC, ?
∠ABC=∠ECD=90°, ? 所以 △ABD∽△ECD, ?
答: 两岸间的大致距离为100米. ? 我们还可以在河对岸选定一目标点A,再在河的一边选点D和 E,使DE⊥AD,然后,再选点B,作BC∥DE,与视线EA相交于点C。此时,测得DE , BC, BD, 就可以求两岸间的大致距离AB了。探究:你还能想出别的方法测量河宽吗?为了测量一池塘的宽AB你能利用相似三角形的性质来解决吗?ABBEADC练习2.为了测量一池塘的宽AB,在岸边找到了一点C,使AC⊥AB,在AC上找到一点D,在BC上找到一点E,使DE⊥AC,测出AD=30m,DC=30m,DE =40m,那么你能算出池塘的宽AB吗?ABCDE解:因为 ∠ACB=∠DCE ,所以 △ABC∽△DEC , 答: 池塘的宽大致为80米. ? ∠CAB=∠CDE=90°,ABCDE课堂小结:一 相似三角形的应用主要有如下两个方面
1 测高(不能直接使用皮尺或刻度尺量的)
2 测距(不能直接测量的两点间的距离)测高的方法
测量不能到达顶部的物体的高度,通常用”在同一时刻物高与影长的比例”的原理解决 测距的方法
测量不能到达两点间的距离,常构造相似三角形求解作业P82 习题 6
2. 测出学校的国旗旗杆的高度努力现在,成就未来衷心感谢你们的合作!
