相似三角形的应用[下学期]
图片预览






文档简介
课件20张PPT。相似三角形的应用
太和三中:王 虎回顾:一.相似三角形的识别对应相等对应成比例夹角三边二.相似三角形的性质对应角对应边对应高对应中线对应角平分线等于相似比等于相似比的平方1、两个相似三角形对应中线之比是1:2,
则对应角平分线之比也是1:2。( )
2、两个相似三角形面积比是1:2,则相似比是1:4。( )
3、△ABC∽△A′B′C′,相似比为2:3,若△ABC周长为6,
则△A′B′C′周长为9。 ( )二、填空:1.如图△ABC中,DE∥BC,且S△ADE=S梯形DBCE,
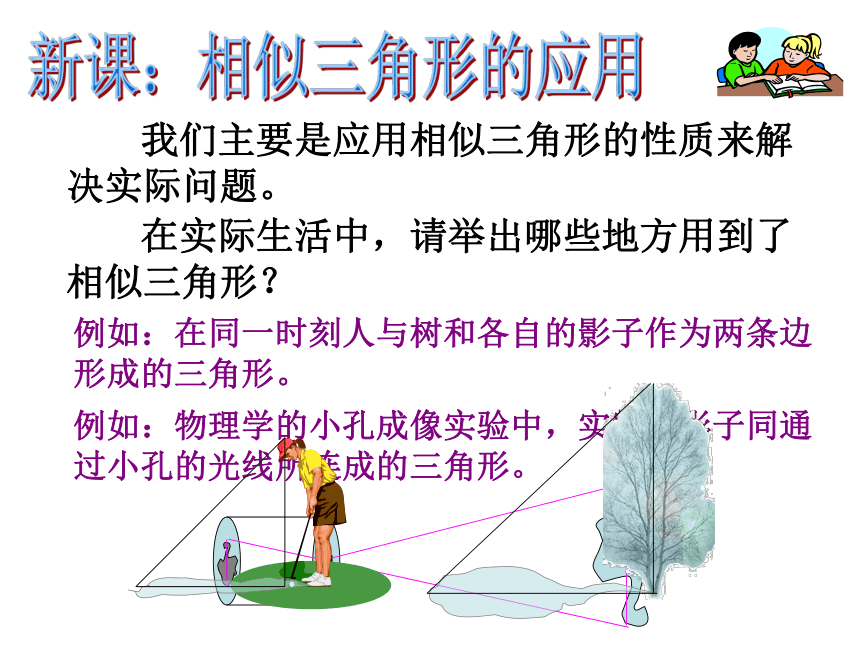
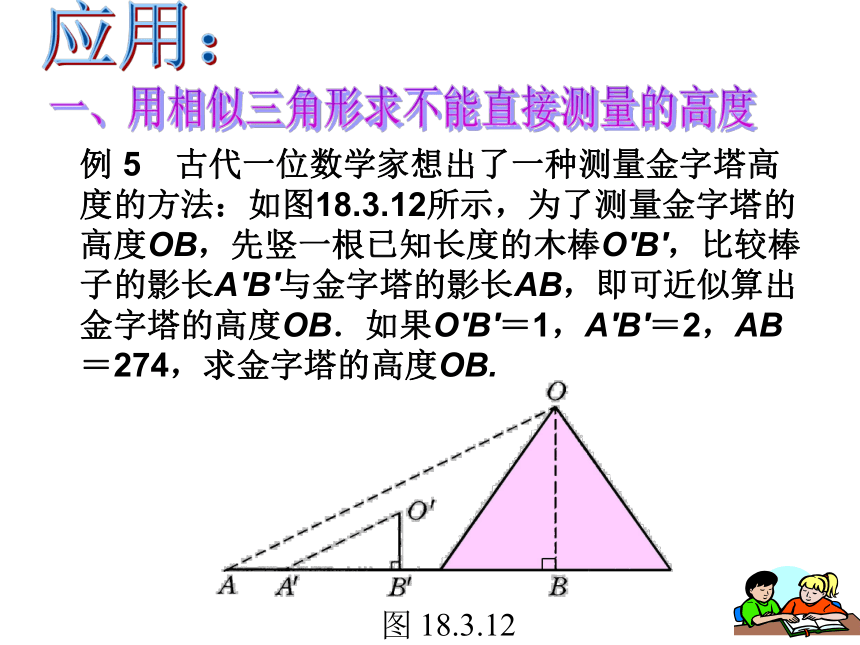
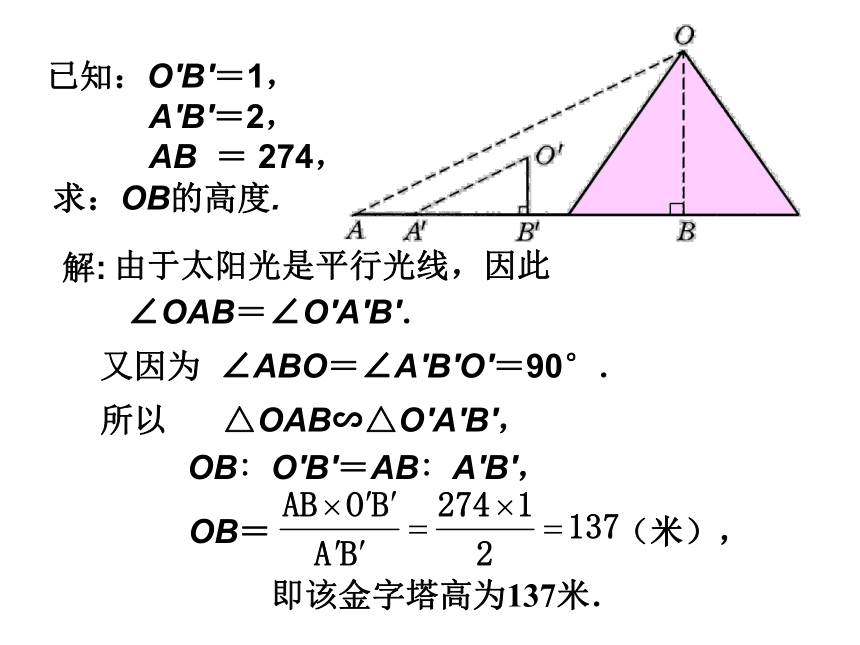
则DE:BC=____.一、判断正误:热身:新课:相似三角形的应用 我们主要是应用相似三角形的性质来解决实际问题。 在实际生活中,请举出哪些地方用到了相似三角形?例如:在同一时刻人与树和各自的影子作为两条边形成的三角形。例如:物理学的小孔成像实验中,实物与影子同通过小孔的光线所连成的三角形。埃及风景小小考古家: 埃及著名的考古专家穆罕穆德决定重新测量胡夫金字塔的高度.在一个烈日高照的上午.他和儿子小穆罕穆德来到了金字塔脚下,他想考一考年仅14岁的小穆罕穆德.给你一条2米高的木杆,一把皮尺,一面平面镜.你能利用所学知识来测出塔高吗?2米木杆皮尺平面镜例 5 古代一位数学家想出了一种测量金字塔高度的方法:如图18.3.12所示,为了测量金字塔的高度OB,先竖一根已知长度的木棒O′B′,比较棒子的影长A′B′与金字塔的影长AB,即可近似算出金字塔的高度OB.如果O′B′=1,A′B′=2,AB=274,求金字塔的高度OB. 一、用相似三角形求不能直接测量的高度应用:由于太阳光是平行光线,因此 OB= (米), 即该金字塔高为137米. ∠OAB=∠O′A′B′.又因为 ∠ABO=∠A′B′O′=90°.所以 △OAB∽△O′A′B′,OB∶O′B′=AB∶A′B′,已知:O′B′=1,
A′B′=2,
AB = 274,求:OB的高度. 解: 你还有其它的方法吗?ACBDE┐┐ACBDE┐┐例6 如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB. 二、用相似三角形求不能直接测量的宽度 那么 ,解得 AB== 答: 两岸间的大致距离为100米.=100(米).解:因为 ∠ADB=∠EDC,∠ABC=∠ECD=90°,所以 △ABD∽△ECD,已知:BD=120米,
DC=60米,
EC=50米,求:两岸间的大致距离AB. 1、在同一时刻物体的高度与它的影长成正比例,在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为60米,那么高楼的高度是多少米?解:设高楼的高度为X米,则答:楼高36米.体验: 2、如图,小明在打网球时,使球恰好能打过网,而且落在离网5米的位置上,求球拍击球的高度h.方法提炼:在两个相似三角形中,若已知两组对应边中三边的长,利用相似三角形对应边成比例很容易求出第四边的长。 如图,已知零件的外径为a,要求它的厚度x,需先求出内孔的直径AB,现用一个交叉卡钳(两条尺长AC和BD相等)去量,若OA:OC=OB:OD=n,且量得CD=b,求厚度x。O思考:(分析:如图,要想求厚度x,根据条件可知,首先得求出内孔直径AB。而在图中可构造出相似形,通过相似形的性质,从而求出AB的长度。)O课堂小结:一 、相似三角形的应用主要有如下两个方面
1 测高(不能直接使用皮尺或刻度尺量的)
2 测距(不能直接测量的两点间的距离)、测高的方法
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长的比例”的原理解决 、测距的方法
测量不能到达两点间的距离,常构造相似三角形求解解决实际问题时(如测高、测距),
一般有以下步骤:①审题 ②构建图形
③利用相似解决问题谈谈你的收获努力现在,成就未来80630136@51uc.com衷心感谢你们的合作!
太和三中:王 虎回顾:一.相似三角形的识别对应相等对应成比例夹角三边二.相似三角形的性质对应角对应边对应高对应中线对应角平分线等于相似比等于相似比的平方1、两个相似三角形对应中线之比是1:2,
则对应角平分线之比也是1:2。( )
2、两个相似三角形面积比是1:2,则相似比是1:4。( )
3、△ABC∽△A′B′C′,相似比为2:3,若△ABC周长为6,
则△A′B′C′周长为9。 ( )二、填空:1.如图△ABC中,DE∥BC,且S△ADE=S梯形DBCE,
则DE:BC=____.一、判断正误:热身:新课:相似三角形的应用 我们主要是应用相似三角形的性质来解决实际问题。 在实际生活中,请举出哪些地方用到了相似三角形?例如:在同一时刻人与树和各自的影子作为两条边形成的三角形。例如:物理学的小孔成像实验中,实物与影子同通过小孔的光线所连成的三角形。埃及风景小小考古家: 埃及著名的考古专家穆罕穆德决定重新测量胡夫金字塔的高度.在一个烈日高照的上午.他和儿子小穆罕穆德来到了金字塔脚下,他想考一考年仅14岁的小穆罕穆德.给你一条2米高的木杆,一把皮尺,一面平面镜.你能利用所学知识来测出塔高吗?2米木杆皮尺平面镜例 5 古代一位数学家想出了一种测量金字塔高度的方法:如图18.3.12所示,为了测量金字塔的高度OB,先竖一根已知长度的木棒O′B′,比较棒子的影长A′B′与金字塔的影长AB,即可近似算出金字塔的高度OB.如果O′B′=1,A′B′=2,AB=274,求金字塔的高度OB. 一、用相似三角形求不能直接测量的高度应用:由于太阳光是平行光线,因此 OB= (米), 即该金字塔高为137米. ∠OAB=∠O′A′B′.又因为 ∠ABO=∠A′B′O′=90°.所以 △OAB∽△O′A′B′,OB∶O′B′=AB∶A′B′,已知:O′B′=1,
A′B′=2,
AB = 274,求:OB的高度. 解: 你还有其它的方法吗?ACBDE┐┐ACBDE┐┐例6 如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB. 二、用相似三角形求不能直接测量的宽度 那么 ,解得 AB== 答: 两岸间的大致距离为100米.=100(米).解:因为 ∠ADB=∠EDC,∠ABC=∠ECD=90°,所以 △ABD∽△ECD,已知:BD=120米,
DC=60米,
EC=50米,求:两岸间的大致距离AB. 1、在同一时刻物体的高度与它的影长成正比例,在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为60米,那么高楼的高度是多少米?解:设高楼的高度为X米,则答:楼高36米.体验: 2、如图,小明在打网球时,使球恰好能打过网,而且落在离网5米的位置上,求球拍击球的高度h.方法提炼:在两个相似三角形中,若已知两组对应边中三边的长,利用相似三角形对应边成比例很容易求出第四边的长。 如图,已知零件的外径为a,要求它的厚度x,需先求出内孔的直径AB,现用一个交叉卡钳(两条尺长AC和BD相等)去量,若OA:OC=OB:OD=n,且量得CD=b,求厚度x。O思考:(分析:如图,要想求厚度x,根据条件可知,首先得求出内孔直径AB。而在图中可构造出相似形,通过相似形的性质,从而求出AB的长度。)O课堂小结:一 、相似三角形的应用主要有如下两个方面
1 测高(不能直接使用皮尺或刻度尺量的)
2 测距(不能直接测量的两点间的距离)、测高的方法
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长的比例”的原理解决 、测距的方法
测量不能到达两点间的距离,常构造相似三角形求解解决实际问题时(如测高、测距),
一般有以下步骤:①审题 ②构建图形
③利用相似解决问题谈谈你的收获努力现在,成就未来80630136@51uc.com衷心感谢你们的合作!
