相似三角形的应用[下学期]
图片预览


文档简介
课件13张PPT。相似三角形
的应用1、两个相似三角形对应中线之比是1:2,则对应角平分线之比也是1:2。( )
2、两个相似三角形面积比是1:2,则相似比是1:4。( )
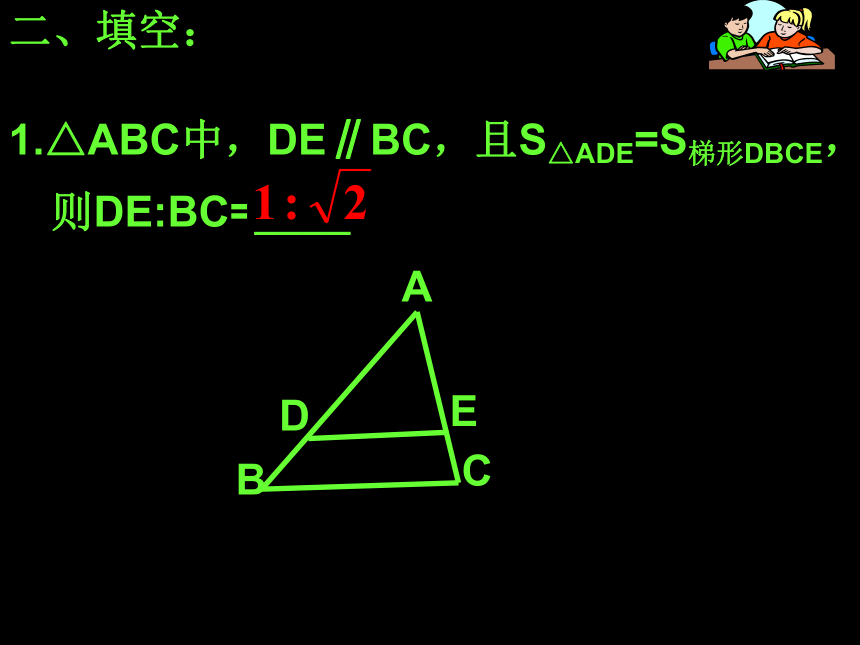
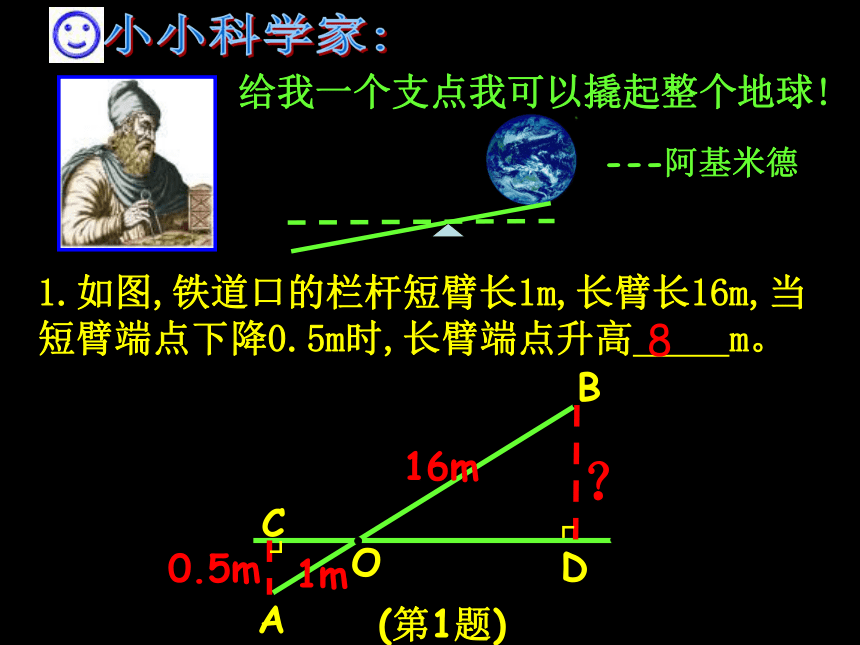
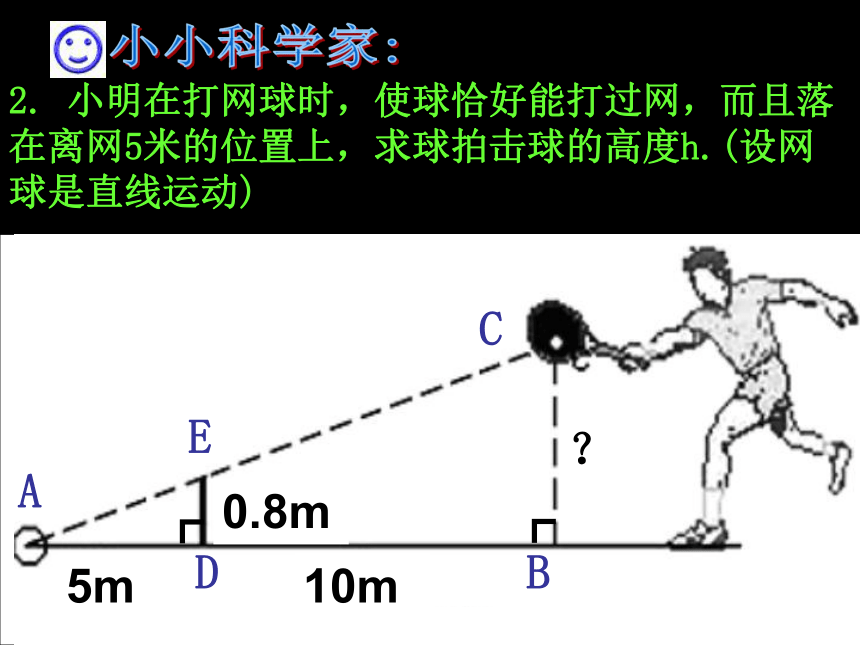
3、△ABC∽△A′B′C′ ,相似比为2:3,若△ABC周长为6,则△A′B′C′周长为9。 ( )一、判断正误:×√√二、填空:1.△ABC中,DE∥BC,且S△ADE=S梯形DBCE,则DE:BC=____.小小科学家:1.如图,铁道口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高 m。 1m16m0.5m8给我一个支点我可以撬起整个地球!---阿基米德?2. 小明在打网球时,使球恰好能打过网,而且落在离网5米的位置上,求球拍击球的高度h.(设网球是直线运动)
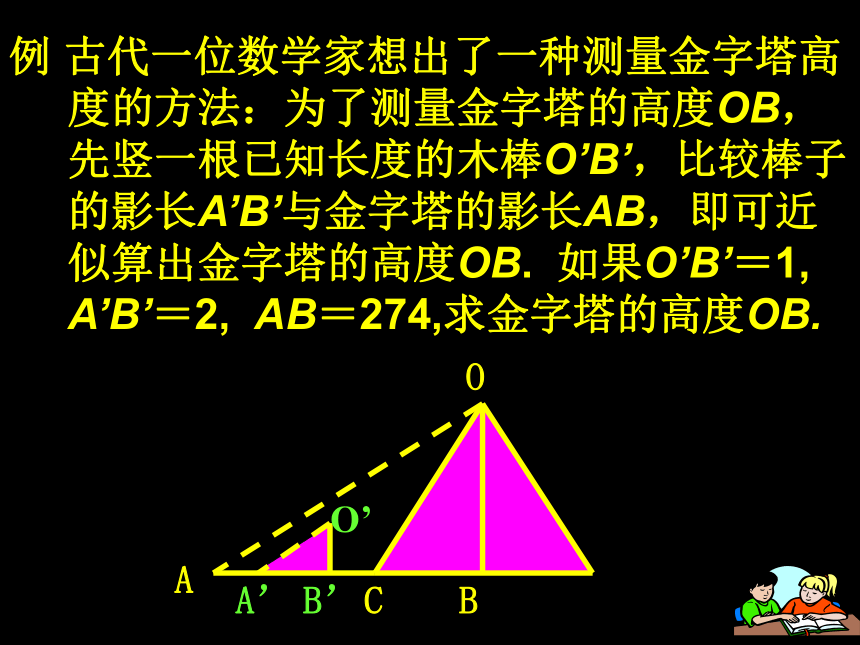
ADBCE┏┏小小科学家:0.8m5m10m?例 古代一位数学家想出了一种测量金字塔高度的方法:为了测量金字塔的高度OB,先竖一根已知长度的木棒O’B’,比较棒子的影长A’B’与金字塔的影长AB,即可近似算出金字塔的高度OB. 如果O’B’=1, A’B’=2, AB=274,求金字塔的高度OB.解: ∵太阳光是平行光线∴该金字塔高为137米. ∴∠OAB=∠O’A’B’.∵ ∠ABO=∠A’B’O’=90°.∴△OAB∽△O’A’B’已知:O’B’=1,A’B’=2,AB = 274,求:OB的高度. ∴OB=137ACBDE┐┐ACBDE┐┐例为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB ·····BACDE∟∟1 答: 两岸间的大致距离为100米.∴AB=100解: ∵∠1=∠2,∠B=∠C=90°∴△ABD∽△ECD已知:BD=120米,DC=60米, EC=50米求:两岸间的大致距离AB. ·BACDE∟∟2已知零件的外径为a,要求它的厚度x,需先求出内孔的直径AB,现用一个交叉卡钳(两条尺长AC和BD相等)去量,若OA:OC=OB:OD=n,且量得CD=b,求AB。∴△AOB∽△COD∠AOB=∠COD解: ∵OA:OC=OB:OD=n ∴AB=bn努力现在,成就未来
的应用1、两个相似三角形对应中线之比是1:2,则对应角平分线之比也是1:2。( )
2、两个相似三角形面积比是1:2,则相似比是1:4。( )
3、△ABC∽△A′B′C′ ,相似比为2:3,若△ABC周长为6,则△A′B′C′周长为9。 ( )一、判断正误:×√√二、填空:1.△ABC中,DE∥BC,且S△ADE=S梯形DBCE,则DE:BC=____.小小科学家:1.如图,铁道口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高 m。 1m16m0.5m8给我一个支点我可以撬起整个地球!---阿基米德?2. 小明在打网球时,使球恰好能打过网,而且落在离网5米的位置上,求球拍击球的高度h.(设网球是直线运动)
ADBCE┏┏小小科学家:0.8m5m10m?例 古代一位数学家想出了一种测量金字塔高度的方法:为了测量金字塔的高度OB,先竖一根已知长度的木棒O’B’,比较棒子的影长A’B’与金字塔的影长AB,即可近似算出金字塔的高度OB. 如果O’B’=1, A’B’=2, AB=274,求金字塔的高度OB.解: ∵太阳光是平行光线∴该金字塔高为137米. ∴∠OAB=∠O’A’B’.∵ ∠ABO=∠A’B’O’=90°.∴△OAB∽△O’A’B’已知:O’B’=1,A’B’=2,AB = 274,求:OB的高度. ∴OB=137ACBDE┐┐ACBDE┐┐例为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB ·····BACDE∟∟1 答: 两岸间的大致距离为100米.∴AB=100解: ∵∠1=∠2,∠B=∠C=90°∴△ABD∽△ECD已知:BD=120米,DC=60米, EC=50米求:两岸间的大致距离AB. ·BACDE∟∟2已知零件的外径为a,要求它的厚度x,需先求出内孔的直径AB,现用一个交叉卡钳(两条尺长AC和BD相等)去量,若OA:OC=OB:OD=n,且量得CD=b,求AB。∴△AOB∽△COD∠AOB=∠COD解: ∵OA:OC=OB:OD=n ∴AB=bn努力现在,成就未来
