2005年相似三角形的应用[下学期] 华东师大[下学期]
文档属性
| 名称 | 2005年相似三角形的应用[下学期] 华东师大[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 331.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-06-02 20:13:00 | ||
图片预览

文档简介
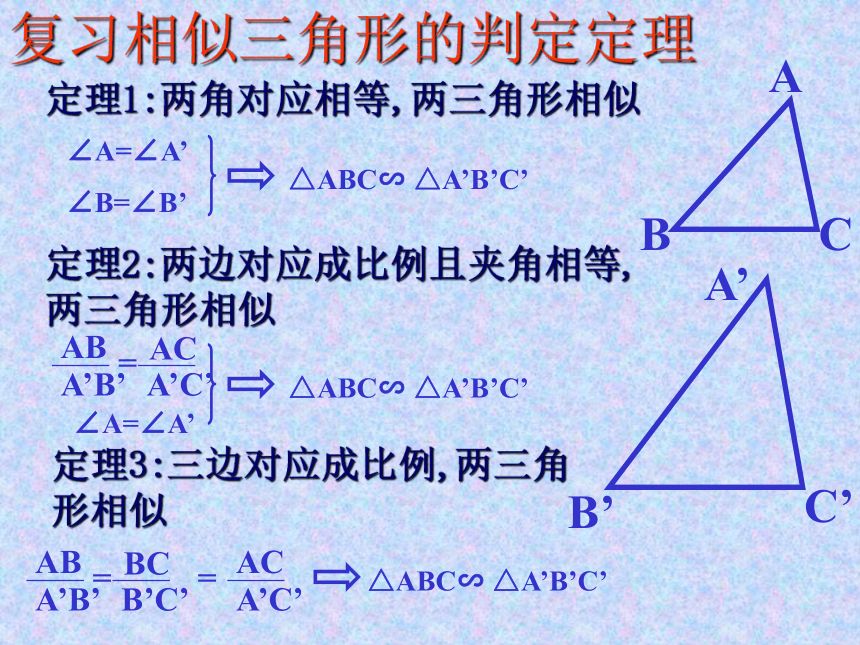
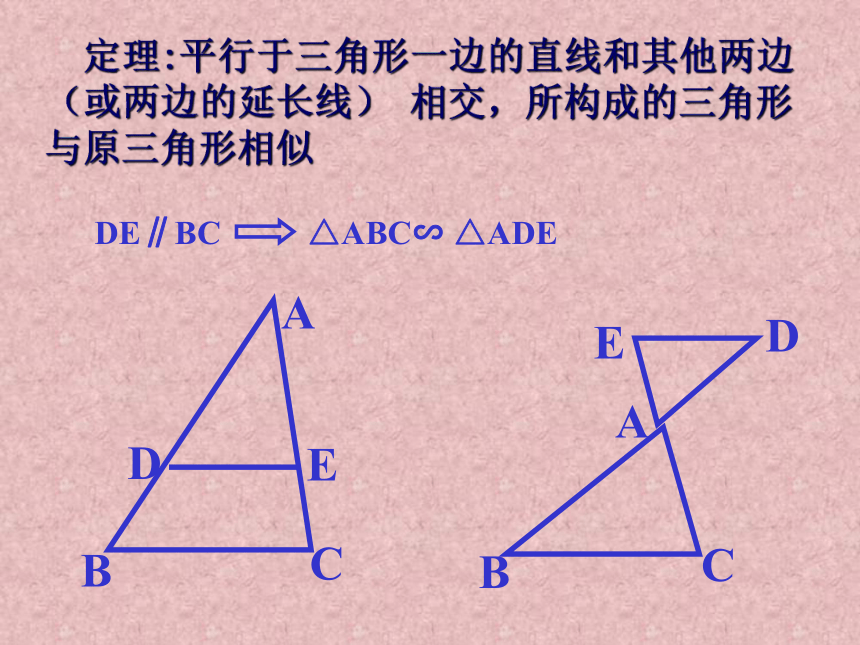
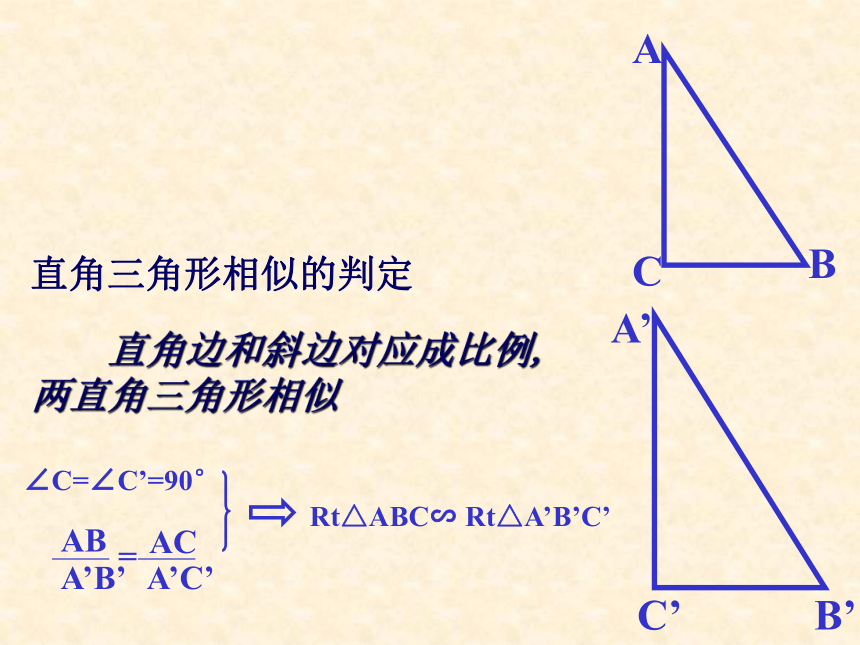
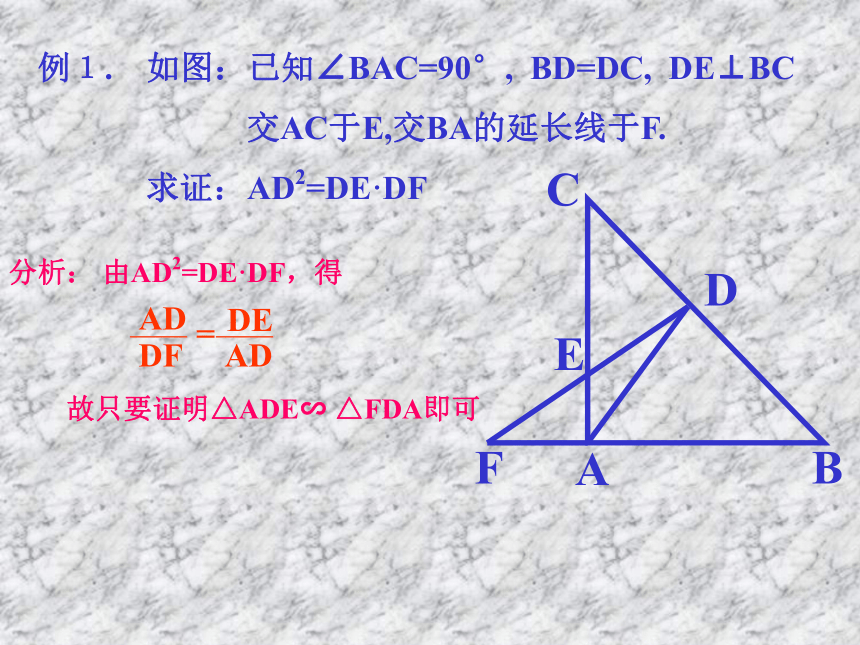
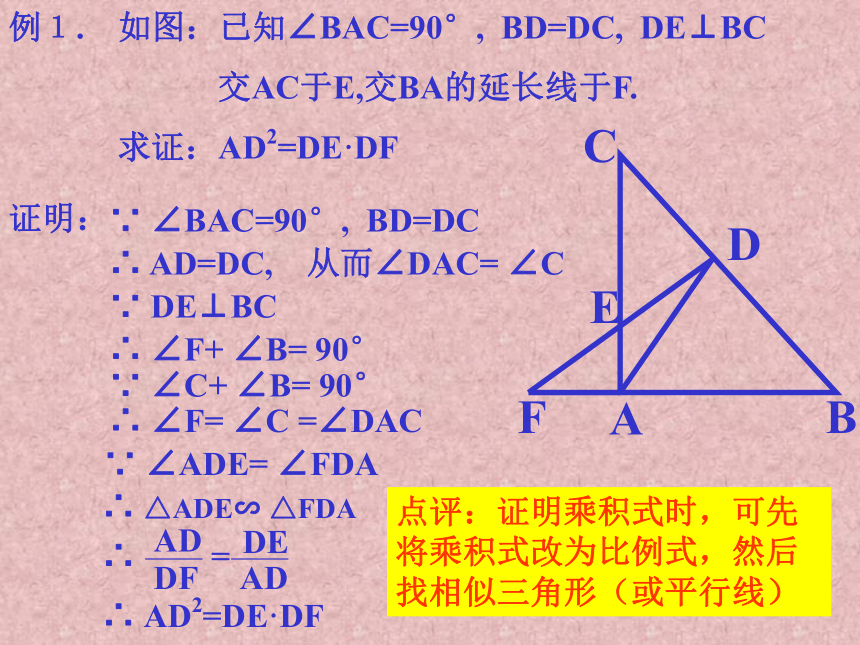
课件15张PPT。相似三角形的应用复习相似三角形的判定定理定理1:两角对应相等,两三角形相似定理2:两边对应成比例且夹角相等,两三角形相似定理3:三边对应成比例,两三角形相似 定理:平行于三角形一边的直线和其他两边 (或两边的延长线) 相交,所构成的三角形与原三角形相似直角三角形相似的判定 直角边和斜边对应成比例,两直角三角形相似FEDCBA例1. 如图:已知∠BAC=90°, BD=DC, DE⊥BC
交AC于E,交BA的延长线于F.
求证:AD2=DE·DF由AD2=DE·DF,得故只要证明△ADE∽ △FDA即可分析:例1. 如图:已知∠BAC=90°, BD=DC, DE⊥BC
交AC于E,交BA的延长线于F.
求证:AD2=DE·DF证明:∴ ∠F= ∠C =∠DAC∵ ∠BAC=90°, BD=DC∵ DE⊥BC∵ ∠C+ ∠B= 90°∵ ∠ADE= ∠FDA∴ AD=DC, 从而∠DAC= ∠C∴ ∠F+ ∠B= 90°∴ △ADE∽ △FDA∴ AD2=DE·DF点评:证明乘积式时,可先将乘积式改为比例式,然后找相似三角形(或平行线)练习1 如图:D为△ABC的底边BC的延长线上一点,
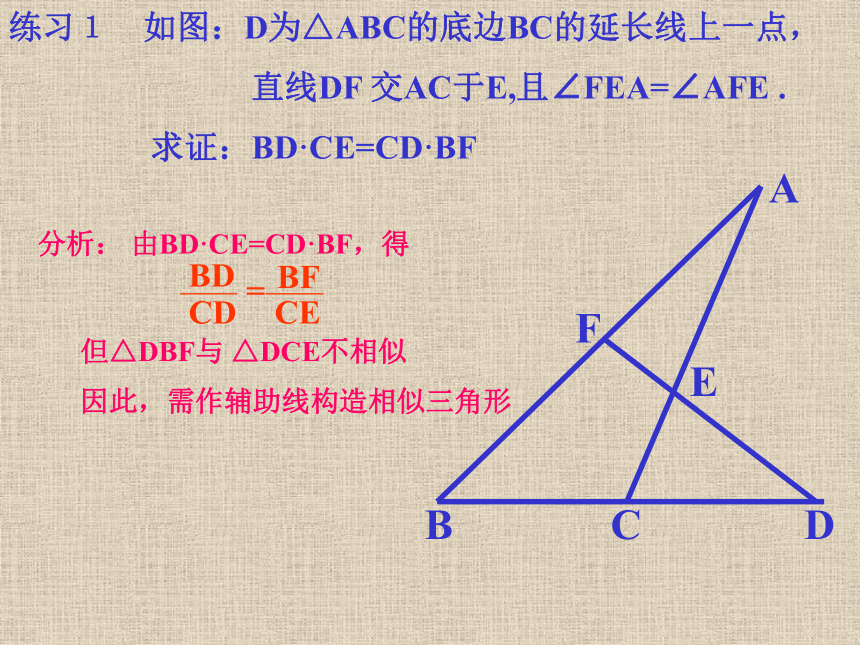
直线DF 交AC于E,且∠FEA=∠AFE .
求证:BD·CE=CD·BFFEDCBA由BD·CE=CD·BF,得分析:但△DBF与 △DCE不相似因此,需作辅助线构造相似三角形练习1 如图:D为△ABC的底边BC的延长线上一点,
直线DF 交AC于E,且∠FEA=∠AFE .
求证:BD·CE=CD·BFFEDCBAG方法一:过点C作CG∥AB,交DF于G 则△DCG∽ △DBF 故再证CG=CE 即可FEDCBAG方法二:过点C作CG∥DF,交AB于G 故再证FG=CE 即可练习1 如图:D为△ABC的底边BC的延长线上一点,
直线DF 交AC于E,且∠FEA=∠AFE .
求证:BD·CE=CD·BFFEDCBAG练习1 如图:D为△ABC的底边BC的延长线上一点,
直线DF 交AC于E,且∠FEA=∠AFE .
求证:BD·CE=CD·BF方法二:过点B作BG∥DF,
交DF的延长线于G 故再证BG=BF 即可则△DCE∽ △DBG 例2. 如图:在Rt△ABC中,有正方形 DEFG,且E、F
在斜边BC上,D、G分别在AB、AC上.
求证:EF2=BE·FCGFEDCBA分析:由EF2=BE·FC,得但EF、BE、FC都在同一直线上
无法利用相似三角形.由于EF是正方形的边长,
故可用BE、FC相关的三角形
的边DE与FG来代替.只要证△GFC∽△BED即可. 例2. 如图:在Rt△ABC中,有正方形 DEFG,且E、F
在斜边BC上,D、G分别在AB、AC上.
求证:EF2=BE·FC证明:又∵ ∠B+∠C=90°,∠B+∠BDE=90°点评:证明共线的线段比例式时,将某些线段用其他线段代替,以便构成相似三角形.这是证明比例式和乘积式的常用方法之一.练习2 如图: 已知△ABC 中,AD平分∠BAC ,
EF是AD的中垂线,EF 交BC的延长线于F .
求证:FD2=FC·FBFEDCBA分析:由FD2=FC·FB,得但FD、FC、FB都在
同一直线上,无法
利用相似三角形.由于FD=FA,替
换后可形成相似三角形.只要证△FAB∽△FCA即可. 小 结1、判定两个三角形相似的方法(1)
(2)
(3)
(4)
(5)两角对应相等,两三角形相似两边对应成比例且夹角相等,两三角形相似三边对应成比例,两三角形相似直角边和斜边对应成比例,两直角三角形相似2、证比例式(或乘积式)的常用方法证明乘积式时,可先将乘积式改为比例式,然后找相似三角形(或平行线)3、证同一直线上的线段的比例式(或乘积式)的常用技巧证明共线的线段比例式时,将某些线段用其他线段代替,以便构成相似三角形. 这是证明比例式和乘积式的常用方法之一.平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似再见
交AC于E,交BA的延长线于F.
求证:AD2=DE·DF由AD2=DE·DF,得故只要证明△ADE∽ △FDA即可分析:例1. 如图:已知∠BAC=90°, BD=DC, DE⊥BC
交AC于E,交BA的延长线于F.
求证:AD2=DE·DF证明:∴ ∠F= ∠C =∠DAC∵ ∠BAC=90°, BD=DC∵ DE⊥BC∵ ∠C+ ∠B= 90°∵ ∠ADE= ∠FDA∴ AD=DC, 从而∠DAC= ∠C∴ ∠F+ ∠B= 90°∴ △ADE∽ △FDA∴ AD2=DE·DF点评:证明乘积式时,可先将乘积式改为比例式,然后找相似三角形(或平行线)练习1 如图:D为△ABC的底边BC的延长线上一点,
直线DF 交AC于E,且∠FEA=∠AFE .
求证:BD·CE=CD·BFFEDCBA由BD·CE=CD·BF,得分析:但△DBF与 △DCE不相似因此,需作辅助线构造相似三角形练习1 如图:D为△ABC的底边BC的延长线上一点,
直线DF 交AC于E,且∠FEA=∠AFE .
求证:BD·CE=CD·BFFEDCBAG方法一:过点C作CG∥AB,交DF于G 则△DCG∽ △DBF 故再证CG=CE 即可FEDCBAG方法二:过点C作CG∥DF,交AB于G 故再证FG=CE 即可练习1 如图:D为△ABC的底边BC的延长线上一点,
直线DF 交AC于E,且∠FEA=∠AFE .
求证:BD·CE=CD·BFFEDCBAG练习1 如图:D为△ABC的底边BC的延长线上一点,
直线DF 交AC于E,且∠FEA=∠AFE .
求证:BD·CE=CD·BF方法二:过点B作BG∥DF,
交DF的延长线于G 故再证BG=BF 即可则△DCE∽ △DBG 例2. 如图:在Rt△ABC中,有正方形 DEFG,且E、F
在斜边BC上,D、G分别在AB、AC上.
求证:EF2=BE·FCGFEDCBA分析:由EF2=BE·FC,得但EF、BE、FC都在同一直线上
无法利用相似三角形.由于EF是正方形的边长,
故可用BE、FC相关的三角形
的边DE与FG来代替.只要证△GFC∽△BED即可. 例2. 如图:在Rt△ABC中,有正方形 DEFG,且E、F
在斜边BC上,D、G分别在AB、AC上.
求证:EF2=BE·FC证明:又∵ ∠B+∠C=90°,∠B+∠BDE=90°点评:证明共线的线段比例式时,将某些线段用其他线段代替,以便构成相似三角形.这是证明比例式和乘积式的常用方法之一.练习2 如图: 已知△ABC 中,AD平分∠BAC ,
EF是AD的中垂线,EF 交BC的延长线于F .
求证:FD2=FC·FBFEDCBA分析:由FD2=FC·FB,得但FD、FC、FB都在
同一直线上,无法
利用相似三角形.由于FD=FA,替
换后可形成相似三角形.只要证△FAB∽△FCA即可. 小 结1、判定两个三角形相似的方法(1)
(2)
(3)
(4)
(5)两角对应相等,两三角形相似两边对应成比例且夹角相等,两三角形相似三边对应成比例,两三角形相似直角边和斜边对应成比例,两直角三角形相似2、证比例式(或乘积式)的常用方法证明乘积式时,可先将乘积式改为比例式,然后找相似三角形(或平行线)3、证同一直线上的线段的比例式(或乘积式)的常用技巧证明共线的线段比例式时,将某些线段用其他线段代替,以便构成相似三角形. 这是证明比例式和乘积式的常用方法之一.平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似再见
