19.1 变量与函数讲义同步学案(含解析)
文档属性
| 名称 | 19.1 变量与函数讲义同步学案(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-03 17:57:15 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版八年级19.1变量与函数讲义
一、知识点剖析
知识点一、 变量与函数
变量:在一个变化过程中数值发生变化的量。
常量:在一个变化过程中数值始终不变的量。
【注意】1)变量可变,而常量不变。
2)常量和变量的区分:在某个变化过程中该量的值是否发生变化。
知识点二、函数的定义
1.一般的,在一个变化过程中,如果有两个变量x和y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就把x称为自变量,y就叫做是x的函数。
【函数概念的解读】1)有两个变量。
2)一个变量的数值随另一个变量的数值变化而变化。
3)对于自变量每一个确定的值,函数有且只有一个值与之对应。
4)y叫x的函数
2.函数自变量的取值范围:一般的,一个函数的自变量x允许取值的范围,叫做这个函数的取值范围.
3.确定函数自变量取值范围的方法:
1)关系式为整式时,函数定义域为全体实数;
2)关系式含有分式时,分式的分母不等于零;
3)关系式含有二次根式时,被开方数大于等于零;
4)关系式中含有指数为零的式子时,底数不等于零;
5)实际问题中函数定义域要和实际情况相符合,使之有意义。
4.函数值概念:如果在自变量取值范围内给定一个值a,函数对应的值为b,那么b叫做当自变量取值为a时的函数值。
5.函数解析式:用来表示函数关系的数学式子叫做函数解析式或函数关系式。
6.函数的取值范围的确定:使函数有意义的自变量的全体取值,叫做自变量的取值范围。
7.函数图像上点的坐标与解析式之间的关系:
1)将点的坐标代入到解析式中,如解析式两边成立,则点在解析式上,反之,不在。
2)两个函数图形交点的坐标就是这两个解析式所组成的方程组的解。
8.函数的三种表示法及其优缺点
解析法:两个变量间的函数关系,有时可以用一个含有这两个变量及数字运算符号的等式表示,这种表示法叫做解析法。
列表法:把自变量x的一系列值和函数y的对应值列成一个表来表示函数关系,这种表示法叫做列表法。
图像法:用图像表示函数关系的方法叫做图像法。
优点 缺点
解析法 准确反映整个变化过程中自变量与函数的关系 求对应值是要经过比较复杂的计算,而且实际问题中有的函数值不一定能用解析式表示
列表法 自变量和与它对应的函数值数据一目了然 所列对应数值个数有限,不容易看出自变量与函数值的对应关系,有局限性
图像法 形象的把自变量和函数值的关系表示出来 图像中只能得到近似的数量关系
1.常量变量
例1.(2022·湖南长沙·八年级期中)把15本书随意放入两个抽屉(每个抽屉内都放),第一个抽屉放入x本,第二个抽屉放入y本,则下列判断错误的是( )
A.15是常量 B.15是变量 C.x是变量 D.y是变量
【变式训练】1
(2023·山东济南市·七年级期中)李师傅到单位附近的加油站加油,如图是所用的加油机上的数据显示牌,则其中的常量是( )
A.金额 B.数量 C.单价 D.金额和数量
2.函数定义
例2.(2022秋·广西贺州·八年级统考期末)下列表达式中,y不是x的函数的是( )
A. B. C. D.
【变式训练】2.
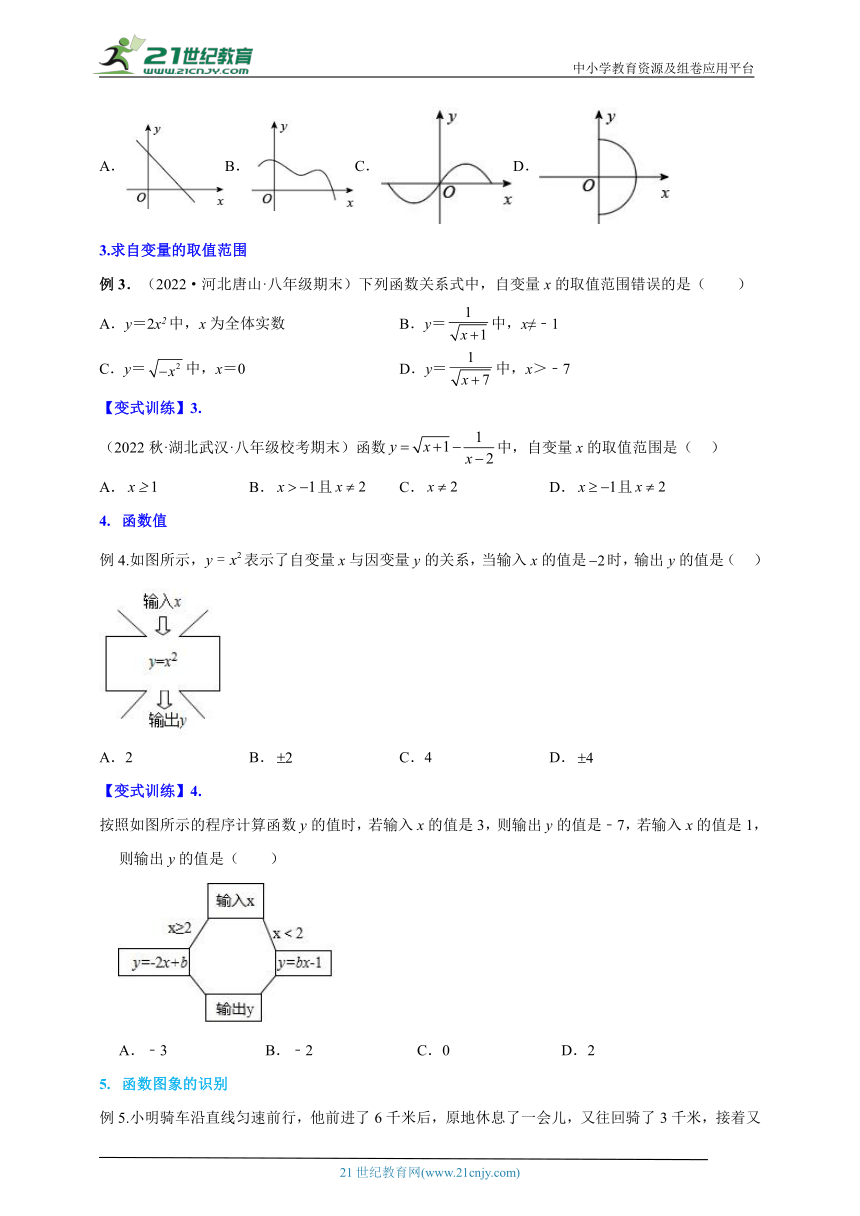
(2022秋·安徽六安·八年级统考期中)如图,下列各曲线中,不是的函数的是( )
A.B.C.D.
3.求自变量的取值范围
例3.(2022·河北唐山·八年级期末)下列函数关系式中,自变量x的取值范围错误的是( )
A.y=2x2中,x为全体实数 B.y=中,x≠﹣1
C.y=中,x=0 D.y=中,x>﹣7
【变式训练】3.
(2022秋·湖北武汉·八年级校考期末)函数中,自变量x的取值范围是( )
A. B.且 C. D.且
函数值
例4.如图所示,表示了自变量x与因变量y的关系,当输入x的值是时,输出y的值是( )
A.2 B. C.4 D.
【变式训练】4.
按照如图所示的程序计算函数y的值时,若输入x的值是3,则输出y的值是﹣7,若输入x的值是1,则输出y的值是( )
A.﹣3 B.﹣2 C.0 D.2
函数图象的识别
例5.小明骑车沿直线匀速前行,他前进了6千米后,原地休息了一会儿,又往回骑了3千米,接着又调头骑了9千米.下列能反映小明离开的距离与骑车时间的函数关系的大致图象是( )
A. B. C.D.
【变式训练】
为积极响应党和国家精准扶贫的号召,某扶贫工作队步行前往扶贫点开展入户调查。队员们先匀速步行一段时间,途中休息几分钟后加快了步行速度,最终按原计划时间到达目的地。设行进时间为t(单位:min),行进的路程为s(单位:m),则能近似刻画s与t之间的函数关系的大致图象是( )
A. B.
C. D.
6.从函数图象获取信息
例6.(2022秋·安徽六安·八年级统考期末)火车匀速通过隧道时,火车在隧道内的长度y(米)与火车行驶时间x(秒)之间的关系用图象描述如图所示,有下列结论:
①火车的长度为100米;②火车的速度为30米/秒;③火车整体都在隧道内的时间为25秒;④隧道长度为1050米.其中正确的结论是( )
A.②③ B.①② C.③④ D.①④
【变式训练】
巴蜀中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动,朱老师先跑.当小明出发时,朱老师已经距起点200米了.他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).据图中给出的信息,解答下列问题:
(1)在上述变化过程中,自变量是______,因变量是______;(2)朱老师的速度为_____米/秒,小明的速度为______米/秒;(3)当小明第一次追上朱老师时,求小明距起点的距离是多少米?
人教版八年级19.1变量与函数讲义(解析版)
例1.(2022·湖南长沙·八年级期中)把15本书随意放入两个抽屉(每个抽屉内都放),第一个抽屉放入x本,第二个抽屉放入y本,则下列判断错误的是( )
A.15是常量 B.15是变量 C.x是变量 D.y是变量
【答案】B
【分析】一个变化的过程中,数值发生变化的量称为变量,数值始终不变的量称为常量,据此判断即可.
【详解】解:把15本书随意放入两个抽屉(每个抽屉内都放),第一个抽屉放入x本,第二个抽屉放入y本.则x和y分别是变量,15是常量.故选:B.
【点睛】本题考查函数的基础:常量与变量,熟练掌握常量与变量的定义是解题关键.
【变式训练】1
(2023·山东济南市·七年级期中)李师傅到单位附近的加油站加油,如图是所用的加油机上的数据显示牌,则其中的常量是( )
A.金额 B.数量 C.单价 D.金额和数量
【答案】C
【分析】根据常量与变量的定义即可判断.
【详解】解:常量是固定不变的量,变量是变化的量,单价是不变的量,而金额是随着数量的变化而变化,
故选:C.
【点睛】本题考查常量与变量,解题的关键是正确理解常量与变量,本题属于基础题型.
2.函数定义
例2.(2022秋·广西贺州·八年级统考期末)下列表达式中,y不是x的函数的是( )
A. B. C. D.
【答案】A
【分析】根据函数的定义即可求解.
【详解】中,x取一个值,y有两个值和其对应,故A选项符合题意;
中,x取一个值,y有唯一的值和其对应,故B选项不符合题意;
中,x取一个值,y有唯一的值和其对应,故C选项不符合题意;
中,x取一个值,y有唯一的值和其对应,故D选项不符合题意,
故选:A.
【点睛】本题考查函数的定义,解题的关键是根据函数的定义进行判断.
【变式训练】2.
(2022秋·安徽六安·八年级统考期中)如图,下列各曲线中,不是的函数的是( )
A.B.C.D.
【答案】D
【分析】对于自变量x的每一个确定的值y都有唯一的确定值与其对应,则y是x的函数,根据函数的定义解答即可.
【详解】解:A、对于自变量的每一个值,因变量都有唯一的值与它对应,所以是的函数,故A不符合题意;
B、对于自变量的每一个值,因变量都有唯一的值与它对应,所以是的函数,故B不符合题意;
C、对于自变量的每一个值,因变量都有唯一的值与它对应,所以是的函数,故C不符合题意;
D、对于自变量的每一个值,因变量不是都有唯一的值与它对应,所以不是的函数,故D符合题意;
故选:D.
【点睛】此题考查函数的定义,函数图象,结合函数图象正确理解函数的定义是解题的关键.
3.求自变量的取值范围
例3.(2022·河北唐山·八年级期末)下列函数关系式中,自变量x的取值范围错误的是( )
A.y=2x2中,x为全体实数 B.y=中,x≠﹣1
C.y=中,x=0 D.y=中,x>﹣7
【答案】B
【分析】根据二次根式的被开方数是非负数、分母不为0列出不等式,解不等式,判断即可.
【详解】解:A、y=2x2中,x为全体实数,自变量x的取值范围正确,不符合题意;
B、y=,x>﹣1,本选项自变量x的取值范围错误,符合题意;
C、y=,x=0,自变量x的取值范围正确,不符合题意;
D、y=,x>﹣7,自变量x的取值范围正确,不符合题意;故选:B.
【点睛】本题考查的是函数自变量的取值范围的确定,掌握二次根式的被开方数是非负数、分母不为0是解题的关键.
【变式训练】3.
(2022秋·湖北武汉·八年级校考期末)函数中,自变量x的取值范围是( )
A. B.且 C. D.且
【答案】D
【分析】根据二次根式有意义的条件,分式有意义的条件,即可求解 .
【详解】解:根据题意得:,
解得:且.
故选:D
【点睛】本题主要考查了求自变量的取值范围,熟练掌握二次根式有意义的条件,分式有意义的条件是解题的关键.
函数值
例4.如图所示,表示了自变量x与因变量y的关系,当输入x的值是时,输出y的值是( )
A.2 B. C.4 D.
【答案】C
【分析】将代入,求出值即可.
【详解】解:当时,;
故选C.
【点睛】本题考查求函数值.熟练掌握将自变量的值代入函数关系式,即可求出函数值,是解题的关键.
【变式训练】4.
按照如图所示的程序计算函数y的值时,若输入x的值是3,则输出y的值是﹣7,若输入x的值是1,则输出y的值是( )
A.﹣3 B.﹣2 C.0 D.2
【分析】先根据输入x的值是3,则输出y的值是﹣7,得到方程:﹣7=﹣2×3+b,求出b的值,再令x=1,计算出y即可.
【解析】∵输入x的值是3,则输出y的值是﹣7,
∴﹣7=﹣2×3+b,
解得:b=﹣1,
∴当x<2时,y=﹣x﹣1,
∴当x=1时,y=﹣1﹣1=﹣2,
故选:B.
函数图象的识别
例5.小明骑车沿直线匀速前行,他前进了6千米后,原地休息了一会儿,又往回骑了3千米,接着又调头骑了9千米.下列能反映小明离开的距离与骑车时间的函数关系的大致图象是( )
A. B. C.D.
【答案】C
【分析】依据小明一系列的动作,匀速前往对应的图象是上升的直线,匀速返回对应的图象是下降的直线等即可得出结论.
【详解】解:∵他沿直线匀速行驶6千米,
∴此图象是一段上升的直线,
∵休息了一段时间,
∴图象是一段平行于t轴的直线,
∵沿原路返回3千米,
∴图象是一段下降的直线,
∵调头再前进了9千米,
∴得图象是一段上升的直线.
∴综合考虑得图象是C.
故选:C.
【点睛】本题考查的是动点问题的函数图象、运动变化的规律等基础知识,考查数形结合思想,属于基础题.
【变式训练】
为积极响应党和国家精准扶贫的号召,某扶贫工作队步行前往扶贫点开展入户调查。队员们先匀速步行一段时间,途中休息几分钟后加快了步行速度,最终按原计划时间到达目的地。设行进时间为t(单位:min),行进的路程为s(单位:m),则能近似刻画s与t之间的函数关系的大致图象是( )
A. B.
C. D.
A
【分析】
根据行进的路程和时间之间的关系,确定图象即可得到答案.
【详解】
解:根据题意得,队员的行进路程s(单位:m)与行进时间t(单位:min)之间函数关系的大致图象是
故选:A
【点拨】
本题考查函数图象,正确理解函数自变量与因变量的关系及其实际意义是解题的关键.
6.从函数图象获取信息
例6.(2022秋·安徽六安·八年级统考期末)火车匀速通过隧道时,火车在隧道内的长度y(米)与火车行驶时间x(秒)之间的关系用图象描述如图所示,有下列结论:
①火车的长度为100米;②火车的速度为30米/秒;③火车整体都在隧道内的时间为25秒;④隧道长度为1050米.其中正确的结论是( )
A.②③ B.①② C.③④ D.①④
【答案】A
【分析】根据函数的图象即可确定在段,所用的时间是5秒,路程是150米,则速度是30米秒,进而即可确定其它答案.
【详解】
解:在段,所用的时间是5秒,路程是150米,则速度是30米秒.故②正确;
火车的长度是150米,故①错误;
整个火车都在隧道内的时间是:秒,故③正确;
隧道长是:米,故④错误.
故正确的是:②③.
故选:A.
【点睛】本题主要考查了用函数的图象解决实际问题,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.
【变式训练】
巴蜀中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动,朱老师先跑.当小明出发时,朱老师已经距起点200米了.他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).据图中给出的信息,解答下列问题:
(1)在上述变化过程中,自变量是______,因变量是______;(2)朱老师的速度为_____米/秒,小明的速度为______米/秒;(3)当小明第一次追上朱老师时,求小明距起点的距离是多少米?
【分析】根据函数图象可知,小明4分钟所走的路程为1600米,4~6分钟休息,6~10分钟骑车(2800﹣1600)米,骑车的总路程为2800米,根据路程、速度、时间的关系进行解答即可.
【解析】①根据图象可知,在4~6分钟,路程没有发生变化,所以小依中途休息的时间为:6﹣4=2分钟,故①正确;②根据图象可知,当t=4时,s=1600,所以小依休息前骑车的平均速度为:1600÷4=400(米/分钟),故②正确;③根据图象可知,小依在上述过程中所走的路程为2800米,故③错误;
④小依休息后的骑车的平均速度为:(2800﹣1600)÷(10﹣6)=300(米/分),小依休息前骑车的平均速度为:1600÷4=400(米/分钟),
400>300,所以小依休息前骑车的平均速度大于休息后骑车的平均速度,故④错误;
综上所述,正确的有①②2个.故答案为:①②.
1.在圆周长的计算公式C=2πr中,变量有( )
A.C,π B.C,r C.π,r D.C,2π
2.下列各图象中,y不是x的函数的是( )
A. B.
C. D.
3.寒冷的冬天里我们在利用空调制热调控室内温度的过程中,空调的每小时用电量随开机设置温度的高低而变化,这个问题中自变量是( )
A.每小时用电量 B.室内温度 C.设置温度 D.用电时间
4.根据如图所示的程序计算函数y的值,若输入的x值是﹣1,则输出的y值为( )
A.﹣3 B.﹣2 C.﹣1 D.1
5.在函数y=+(x﹣4)0中,自变量x的取值范围是_____.
6. 小明早上步行去车站,然后坐车去学校.如图象中,能近似的刻画小明离学校的距离随时间变化关系的图象是_____.(填序号)
7.“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了 一觉. 当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终 点……. 用 s1 、s2 分别表示乌龟和兔子所行的路程, t 为时间,则下列图像中与故事情节相吻合的是( )
A.B.C.D.
8.周末,小明骑车从家前往公园,中途休息了一段时间.他从家出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.对于下列说法:①小明中途休息了2分钟;②小明休息前的骑车速度为每分钟400米;③小明所走的路程为4400米;④小明休息前的骑车速度小于休息后的骑车速度.其中正确结论的序号是 .
学以致用答案:
B
【分析】根据变量定义可得答案.
【解析】在圆周长的计算公式C=2πr中,变量有C和r,
故选:B.
B
【分析】函数的定义:在某变化过程中,有两个变量x、y,并且对于x在某个范围内的每一个确定的值,按照对应法则,y都有唯一确定的值和它对应,则x叫自变量,y是x的函数.根据定义再结合图象观察就可以得出结论.
【解析】根据函数定义,如果在某变化过程中,有两个变量x、y,并且对于x在某个范围内的每一个确定的值,按照对应法则,y都有唯一确定的值和它对应.而B中的y的值不具有唯一性,所以不是函数图象.
故选:B.
C
【分析】根据题意分析,自变量是设置温度,因变量是空调的每小时用电量,据此分析即可.
【详解】解:空调的每小时用电量随开机设置温度的高低而变化,这个问题中自变量是设置温度,故选:C.
【点睛】本题考查了自变量与函数关系,理解题意是解题的关键.
C
【分析】由﹣1在﹣2<x≤2之间,把x=﹣1代入y=﹣x2计算即可.
【解析】当x=﹣1时,y=﹣(﹣1)2=﹣1.
故选:C.
x>3且x≠4.
【分析】
结合二次根式的被开方数为非负数,分式的分母不能为零,零的零次幂没有意义等知识点求解自变量取值范围.
【详解】
解:要使函数y=+(x﹣4)0有意义,
则x﹣3>0且x﹣4≠0,
解得x>3且x≠4,
故答案为:x>3且x≠4.
【点拨】
本题主要考查了函数自变量的取值范围,对于实际问题中的函数关系式,自变量的取值除必须使表达式有意义外,还要保证实际问题有意义.
④
【分析】
根据上学,可得离学校的距离越来越小,根据开始步行,可得距离变化慢,后来坐车,可得距离变化快.
【详解】
①距离越来越大,选项错误;
②距离越来越小,但前后变化快慢一样,选项错误;
③距离越来越大,选项错误;
④距离越来越小,且距离先变化慢,后变化快,选项正确;
故答案为:④.
【点拨】
本题考查了函数图象,观察距离随时间的变化是解题关键.
A
【分析】
根据题意,兔子的路程随时间的变化分为3个阶段,由此即可求出答案.
【详解】
解:根据题意:s1一直增加;
s2有三个阶段,第一阶段:s2增加;
第二阶段,由于睡了一觉,所以s2不变;
第三阶段,当它醒来时,发现乌龟快到终点了,于是急忙追赶,s2增加;
∵乌龟先到达终点,即s1在s2的上方.
故选:A.
【点拨】
本题考查变量之间的关系.能够通过图象得到函数是随自变量的增大,知道函数值是增大还是减小,通过图象得到函数是随自变量的增大或减小的快慢.
8.【答案】(1)t,s;(2)2,6;(3)小明距起点的距离为300米.
【分析】(1)观察函数图象即可找出谁是自变量谁是因变
(2)根据速度=路程÷时间,即可分别算出朱老师以及小明的速度;
(3)设t秒时,小明第一次追上朱老师,列出关系式即可解答
【详解】解:(1)在上述变化过程中,自变量是t,因变量是s;
(2)朱老师的速度=2(米/秒),小明的速度为=6(米/秒);故答案为t,s;2,6;
(3)设t秒时,小明第一次追上朱老师根据题意得6t=200+2t,解得t=50(s),则50×6=300(米),
所以当小明第一次追上朱老师时,小明距起点的距离为300米.
【点睛】此题考查一次函数的应用,解题关键在于看懂图中数据。
二、经典例题
学以致用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版八年级19.1变量与函数讲义
一、知识点剖析
知识点一、 变量与函数
变量:在一个变化过程中数值发生变化的量。
常量:在一个变化过程中数值始终不变的量。
【注意】1)变量可变,而常量不变。
2)常量和变量的区分:在某个变化过程中该量的值是否发生变化。
知识点二、函数的定义
1.一般的,在一个变化过程中,如果有两个变量x和y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就把x称为自变量,y就叫做是x的函数。
【函数概念的解读】1)有两个变量。
2)一个变量的数值随另一个变量的数值变化而变化。
3)对于自变量每一个确定的值,函数有且只有一个值与之对应。
4)y叫x的函数
2.函数自变量的取值范围:一般的,一个函数的自变量x允许取值的范围,叫做这个函数的取值范围.
3.确定函数自变量取值范围的方法:
1)关系式为整式时,函数定义域为全体实数;
2)关系式含有分式时,分式的分母不等于零;
3)关系式含有二次根式时,被开方数大于等于零;
4)关系式中含有指数为零的式子时,底数不等于零;
5)实际问题中函数定义域要和实际情况相符合,使之有意义。
4.函数值概念:如果在自变量取值范围内给定一个值a,函数对应的值为b,那么b叫做当自变量取值为a时的函数值。
5.函数解析式:用来表示函数关系的数学式子叫做函数解析式或函数关系式。
6.函数的取值范围的确定:使函数有意义的自变量的全体取值,叫做自变量的取值范围。
7.函数图像上点的坐标与解析式之间的关系:
1)将点的坐标代入到解析式中,如解析式两边成立,则点在解析式上,反之,不在。
2)两个函数图形交点的坐标就是这两个解析式所组成的方程组的解。
8.函数的三种表示法及其优缺点
解析法:两个变量间的函数关系,有时可以用一个含有这两个变量及数字运算符号的等式表示,这种表示法叫做解析法。
列表法:把自变量x的一系列值和函数y的对应值列成一个表来表示函数关系,这种表示法叫做列表法。
图像法:用图像表示函数关系的方法叫做图像法。
优点 缺点
解析法 准确反映整个变化过程中自变量与函数的关系 求对应值是要经过比较复杂的计算,而且实际问题中有的函数值不一定能用解析式表示
列表法 自变量和与它对应的函数值数据一目了然 所列对应数值个数有限,不容易看出自变量与函数值的对应关系,有局限性
图像法 形象的把自变量和函数值的关系表示出来 图像中只能得到近似的数量关系
1.常量变量
例1.(2022·湖南长沙·八年级期中)把15本书随意放入两个抽屉(每个抽屉内都放),第一个抽屉放入x本,第二个抽屉放入y本,则下列判断错误的是( )
A.15是常量 B.15是变量 C.x是变量 D.y是变量
【变式训练】1
(2023·山东济南市·七年级期中)李师傅到单位附近的加油站加油,如图是所用的加油机上的数据显示牌,则其中的常量是( )
A.金额 B.数量 C.单价 D.金额和数量
2.函数定义
例2.(2022秋·广西贺州·八年级统考期末)下列表达式中,y不是x的函数的是( )
A. B. C. D.
【变式训练】2.
(2022秋·安徽六安·八年级统考期中)如图,下列各曲线中,不是的函数的是( )
A.B.C.D.
3.求自变量的取值范围
例3.(2022·河北唐山·八年级期末)下列函数关系式中,自变量x的取值范围错误的是( )
A.y=2x2中,x为全体实数 B.y=中,x≠﹣1
C.y=中,x=0 D.y=中,x>﹣7
【变式训练】3.
(2022秋·湖北武汉·八年级校考期末)函数中,自变量x的取值范围是( )
A. B.且 C. D.且
函数值
例4.如图所示,表示了自变量x与因变量y的关系,当输入x的值是时,输出y的值是( )
A.2 B. C.4 D.
【变式训练】4.
按照如图所示的程序计算函数y的值时,若输入x的值是3,则输出y的值是﹣7,若输入x的值是1,则输出y的值是( )
A.﹣3 B.﹣2 C.0 D.2
函数图象的识别
例5.小明骑车沿直线匀速前行,他前进了6千米后,原地休息了一会儿,又往回骑了3千米,接着又调头骑了9千米.下列能反映小明离开的距离与骑车时间的函数关系的大致图象是( )
A. B. C.D.
【变式训练】
为积极响应党和国家精准扶贫的号召,某扶贫工作队步行前往扶贫点开展入户调查。队员们先匀速步行一段时间,途中休息几分钟后加快了步行速度,最终按原计划时间到达目的地。设行进时间为t(单位:min),行进的路程为s(单位:m),则能近似刻画s与t之间的函数关系的大致图象是( )
A. B.
C. D.
6.从函数图象获取信息
例6.(2022秋·安徽六安·八年级统考期末)火车匀速通过隧道时,火车在隧道内的长度y(米)与火车行驶时间x(秒)之间的关系用图象描述如图所示,有下列结论:
①火车的长度为100米;②火车的速度为30米/秒;③火车整体都在隧道内的时间为25秒;④隧道长度为1050米.其中正确的结论是( )
A.②③ B.①② C.③④ D.①④
【变式训练】
巴蜀中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动,朱老师先跑.当小明出发时,朱老师已经距起点200米了.他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).据图中给出的信息,解答下列问题:
(1)在上述变化过程中,自变量是______,因变量是______;(2)朱老师的速度为_____米/秒,小明的速度为______米/秒;(3)当小明第一次追上朱老师时,求小明距起点的距离是多少米?
人教版八年级19.1变量与函数讲义(解析版)
例1.(2022·湖南长沙·八年级期中)把15本书随意放入两个抽屉(每个抽屉内都放),第一个抽屉放入x本,第二个抽屉放入y本,则下列判断错误的是( )
A.15是常量 B.15是变量 C.x是变量 D.y是变量
【答案】B
【分析】一个变化的过程中,数值发生变化的量称为变量,数值始终不变的量称为常量,据此判断即可.
【详解】解:把15本书随意放入两个抽屉(每个抽屉内都放),第一个抽屉放入x本,第二个抽屉放入y本.则x和y分别是变量,15是常量.故选:B.
【点睛】本题考查函数的基础:常量与变量,熟练掌握常量与变量的定义是解题关键.
【变式训练】1
(2023·山东济南市·七年级期中)李师傅到单位附近的加油站加油,如图是所用的加油机上的数据显示牌,则其中的常量是( )
A.金额 B.数量 C.单价 D.金额和数量
【答案】C
【分析】根据常量与变量的定义即可判断.
【详解】解:常量是固定不变的量,变量是变化的量,单价是不变的量,而金额是随着数量的变化而变化,
故选:C.
【点睛】本题考查常量与变量,解题的关键是正确理解常量与变量,本题属于基础题型.
2.函数定义
例2.(2022秋·广西贺州·八年级统考期末)下列表达式中,y不是x的函数的是( )
A. B. C. D.
【答案】A
【分析】根据函数的定义即可求解.
【详解】中,x取一个值,y有两个值和其对应,故A选项符合题意;
中,x取一个值,y有唯一的值和其对应,故B选项不符合题意;
中,x取一个值,y有唯一的值和其对应,故C选项不符合题意;
中,x取一个值,y有唯一的值和其对应,故D选项不符合题意,
故选:A.
【点睛】本题考查函数的定义,解题的关键是根据函数的定义进行判断.
【变式训练】2.
(2022秋·安徽六安·八年级统考期中)如图,下列各曲线中,不是的函数的是( )
A.B.C.D.
【答案】D
【分析】对于自变量x的每一个确定的值y都有唯一的确定值与其对应,则y是x的函数,根据函数的定义解答即可.
【详解】解:A、对于自变量的每一个值,因变量都有唯一的值与它对应,所以是的函数,故A不符合题意;
B、对于自变量的每一个值,因变量都有唯一的值与它对应,所以是的函数,故B不符合题意;
C、对于自变量的每一个值,因变量都有唯一的值与它对应,所以是的函数,故C不符合题意;
D、对于自变量的每一个值,因变量不是都有唯一的值与它对应,所以不是的函数,故D符合题意;
故选:D.
【点睛】此题考查函数的定义,函数图象,结合函数图象正确理解函数的定义是解题的关键.
3.求自变量的取值范围
例3.(2022·河北唐山·八年级期末)下列函数关系式中,自变量x的取值范围错误的是( )
A.y=2x2中,x为全体实数 B.y=中,x≠﹣1
C.y=中,x=0 D.y=中,x>﹣7
【答案】B
【分析】根据二次根式的被开方数是非负数、分母不为0列出不等式,解不等式,判断即可.
【详解】解:A、y=2x2中,x为全体实数,自变量x的取值范围正确,不符合题意;
B、y=,x>﹣1,本选项自变量x的取值范围错误,符合题意;
C、y=,x=0,自变量x的取值范围正确,不符合题意;
D、y=,x>﹣7,自变量x的取值范围正确,不符合题意;故选:B.
【点睛】本题考查的是函数自变量的取值范围的确定,掌握二次根式的被开方数是非负数、分母不为0是解题的关键.
【变式训练】3.
(2022秋·湖北武汉·八年级校考期末)函数中,自变量x的取值范围是( )
A. B.且 C. D.且
【答案】D
【分析】根据二次根式有意义的条件,分式有意义的条件,即可求解 .
【详解】解:根据题意得:,
解得:且.
故选:D
【点睛】本题主要考查了求自变量的取值范围,熟练掌握二次根式有意义的条件,分式有意义的条件是解题的关键.
函数值
例4.如图所示,表示了自变量x与因变量y的关系,当输入x的值是时,输出y的值是( )
A.2 B. C.4 D.
【答案】C
【分析】将代入,求出值即可.
【详解】解:当时,;
故选C.
【点睛】本题考查求函数值.熟练掌握将自变量的值代入函数关系式,即可求出函数值,是解题的关键.
【变式训练】4.
按照如图所示的程序计算函数y的值时,若输入x的值是3,则输出y的值是﹣7,若输入x的值是1,则输出y的值是( )
A.﹣3 B.﹣2 C.0 D.2
【分析】先根据输入x的值是3,则输出y的值是﹣7,得到方程:﹣7=﹣2×3+b,求出b的值,再令x=1,计算出y即可.
【解析】∵输入x的值是3,则输出y的值是﹣7,
∴﹣7=﹣2×3+b,
解得:b=﹣1,
∴当x<2时,y=﹣x﹣1,
∴当x=1时,y=﹣1﹣1=﹣2,
故选:B.
函数图象的识别
例5.小明骑车沿直线匀速前行,他前进了6千米后,原地休息了一会儿,又往回骑了3千米,接着又调头骑了9千米.下列能反映小明离开的距离与骑车时间的函数关系的大致图象是( )
A. B. C.D.
【答案】C
【分析】依据小明一系列的动作,匀速前往对应的图象是上升的直线,匀速返回对应的图象是下降的直线等即可得出结论.
【详解】解:∵他沿直线匀速行驶6千米,
∴此图象是一段上升的直线,
∵休息了一段时间,
∴图象是一段平行于t轴的直线,
∵沿原路返回3千米,
∴图象是一段下降的直线,
∵调头再前进了9千米,
∴得图象是一段上升的直线.
∴综合考虑得图象是C.
故选:C.
【点睛】本题考查的是动点问题的函数图象、运动变化的规律等基础知识,考查数形结合思想,属于基础题.
【变式训练】
为积极响应党和国家精准扶贫的号召,某扶贫工作队步行前往扶贫点开展入户调查。队员们先匀速步行一段时间,途中休息几分钟后加快了步行速度,最终按原计划时间到达目的地。设行进时间为t(单位:min),行进的路程为s(单位:m),则能近似刻画s与t之间的函数关系的大致图象是( )
A. B.
C. D.
A
【分析】
根据行进的路程和时间之间的关系,确定图象即可得到答案.
【详解】
解:根据题意得,队员的行进路程s(单位:m)与行进时间t(单位:min)之间函数关系的大致图象是
故选:A
【点拨】
本题考查函数图象,正确理解函数自变量与因变量的关系及其实际意义是解题的关键.
6.从函数图象获取信息
例6.(2022秋·安徽六安·八年级统考期末)火车匀速通过隧道时,火车在隧道内的长度y(米)与火车行驶时间x(秒)之间的关系用图象描述如图所示,有下列结论:
①火车的长度为100米;②火车的速度为30米/秒;③火车整体都在隧道内的时间为25秒;④隧道长度为1050米.其中正确的结论是( )
A.②③ B.①② C.③④ D.①④
【答案】A
【分析】根据函数的图象即可确定在段,所用的时间是5秒,路程是150米,则速度是30米秒,进而即可确定其它答案.
【详解】
解:在段,所用的时间是5秒,路程是150米,则速度是30米秒.故②正确;
火车的长度是150米,故①错误;
整个火车都在隧道内的时间是:秒,故③正确;
隧道长是:米,故④错误.
故正确的是:②③.
故选:A.
【点睛】本题主要考查了用函数的图象解决实际问题,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.
【变式训练】
巴蜀中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动,朱老师先跑.当小明出发时,朱老师已经距起点200米了.他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).据图中给出的信息,解答下列问题:
(1)在上述变化过程中,自变量是______,因变量是______;(2)朱老师的速度为_____米/秒,小明的速度为______米/秒;(3)当小明第一次追上朱老师时,求小明距起点的距离是多少米?
【分析】根据函数图象可知,小明4分钟所走的路程为1600米,4~6分钟休息,6~10分钟骑车(2800﹣1600)米,骑车的总路程为2800米,根据路程、速度、时间的关系进行解答即可.
【解析】①根据图象可知,在4~6分钟,路程没有发生变化,所以小依中途休息的时间为:6﹣4=2分钟,故①正确;②根据图象可知,当t=4时,s=1600,所以小依休息前骑车的平均速度为:1600÷4=400(米/分钟),故②正确;③根据图象可知,小依在上述过程中所走的路程为2800米,故③错误;
④小依休息后的骑车的平均速度为:(2800﹣1600)÷(10﹣6)=300(米/分),小依休息前骑车的平均速度为:1600÷4=400(米/分钟),
400>300,所以小依休息前骑车的平均速度大于休息后骑车的平均速度,故④错误;
综上所述,正确的有①②2个.故答案为:①②.
1.在圆周长的计算公式C=2πr中,变量有( )
A.C,π B.C,r C.π,r D.C,2π
2.下列各图象中,y不是x的函数的是( )
A. B.
C. D.
3.寒冷的冬天里我们在利用空调制热调控室内温度的过程中,空调的每小时用电量随开机设置温度的高低而变化,这个问题中自变量是( )
A.每小时用电量 B.室内温度 C.设置温度 D.用电时间
4.根据如图所示的程序计算函数y的值,若输入的x值是﹣1,则输出的y值为( )
A.﹣3 B.﹣2 C.﹣1 D.1
5.在函数y=+(x﹣4)0中,自变量x的取值范围是_____.
6. 小明早上步行去车站,然后坐车去学校.如图象中,能近似的刻画小明离学校的距离随时间变化关系的图象是_____.(填序号)
7.“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了 一觉. 当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终 点……. 用 s1 、s2 分别表示乌龟和兔子所行的路程, t 为时间,则下列图像中与故事情节相吻合的是( )
A.B.C.D.
8.周末,小明骑车从家前往公园,中途休息了一段时间.他从家出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.对于下列说法:①小明中途休息了2分钟;②小明休息前的骑车速度为每分钟400米;③小明所走的路程为4400米;④小明休息前的骑车速度小于休息后的骑车速度.其中正确结论的序号是 .
学以致用答案:
B
【分析】根据变量定义可得答案.
【解析】在圆周长的计算公式C=2πr中,变量有C和r,
故选:B.
B
【分析】函数的定义:在某变化过程中,有两个变量x、y,并且对于x在某个范围内的每一个确定的值,按照对应法则,y都有唯一确定的值和它对应,则x叫自变量,y是x的函数.根据定义再结合图象观察就可以得出结论.
【解析】根据函数定义,如果在某变化过程中,有两个变量x、y,并且对于x在某个范围内的每一个确定的值,按照对应法则,y都有唯一确定的值和它对应.而B中的y的值不具有唯一性,所以不是函数图象.
故选:B.
C
【分析】根据题意分析,自变量是设置温度,因变量是空调的每小时用电量,据此分析即可.
【详解】解:空调的每小时用电量随开机设置温度的高低而变化,这个问题中自变量是设置温度,故选:C.
【点睛】本题考查了自变量与函数关系,理解题意是解题的关键.
C
【分析】由﹣1在﹣2<x≤2之间,把x=﹣1代入y=﹣x2计算即可.
【解析】当x=﹣1时,y=﹣(﹣1)2=﹣1.
故选:C.
x>3且x≠4.
【分析】
结合二次根式的被开方数为非负数,分式的分母不能为零,零的零次幂没有意义等知识点求解自变量取值范围.
【详解】
解:要使函数y=+(x﹣4)0有意义,
则x﹣3>0且x﹣4≠0,
解得x>3且x≠4,
故答案为:x>3且x≠4.
【点拨】
本题主要考查了函数自变量的取值范围,对于实际问题中的函数关系式,自变量的取值除必须使表达式有意义外,还要保证实际问题有意义.
④
【分析】
根据上学,可得离学校的距离越来越小,根据开始步行,可得距离变化慢,后来坐车,可得距离变化快.
【详解】
①距离越来越大,选项错误;
②距离越来越小,但前后变化快慢一样,选项错误;
③距离越来越大,选项错误;
④距离越来越小,且距离先变化慢,后变化快,选项正确;
故答案为:④.
【点拨】
本题考查了函数图象,观察距离随时间的变化是解题关键.
A
【分析】
根据题意,兔子的路程随时间的变化分为3个阶段,由此即可求出答案.
【详解】
解:根据题意:s1一直增加;
s2有三个阶段,第一阶段:s2增加;
第二阶段,由于睡了一觉,所以s2不变;
第三阶段,当它醒来时,发现乌龟快到终点了,于是急忙追赶,s2增加;
∵乌龟先到达终点,即s1在s2的上方.
故选:A.
【点拨】
本题考查变量之间的关系.能够通过图象得到函数是随自变量的增大,知道函数值是增大还是减小,通过图象得到函数是随自变量的增大或减小的快慢.
8.【答案】(1)t,s;(2)2,6;(3)小明距起点的距离为300米.
【分析】(1)观察函数图象即可找出谁是自变量谁是因变
(2)根据速度=路程÷时间,即可分别算出朱老师以及小明的速度;
(3)设t秒时,小明第一次追上朱老师,列出关系式即可解答
【详解】解:(1)在上述变化过程中,自变量是t,因变量是s;
(2)朱老师的速度=2(米/秒),小明的速度为=6(米/秒);故答案为t,s;2,6;
(3)设t秒时,小明第一次追上朱老师根据题意得6t=200+2t,解得t=50(s),则50×6=300(米),
所以当小明第一次追上朱老师时,小明距起点的距离为300米.
【点睛】此题考查一次函数的应用,解题关键在于看懂图中数据。
二、经典例题
学以致用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
