人教版小学数学五年级上册5.2.3《解简单方程》课件(共24张ppt)
文档属性
| 名称 | 人教版小学数学五年级上册5.2.3《解简单方程》课件(共24张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 868.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-03 15:35:28 | ||
图片预览






文档简介
(共24张PPT)
解简单方程
第五单元 简易方程
输入标题
学习目标
在解方程的过程中,培养学生的观察、分析能力,体会到知识间的密切联系,激发学习兴趣。
结合图例,理解用等式性质解方程的方法,学会正确解方程和规范书写格式。
解简单方程
输入标题
探究新知
创设情境
巩固练习
课堂小结
布置作业
什么是等式的基本性质?
问题
等式的基本性质(乘除):
等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
等式的基本性质(加减):
等式两边加上或减去同一个数,左右两边仍然相等。
输入标题
探究新知
创设情境
巩固练习
课堂小结
布置作业
问题
等式的基本性质在方程中同样适用吗?为什么?
同样适用,因为方程也是等式。
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
探究解方程的方法
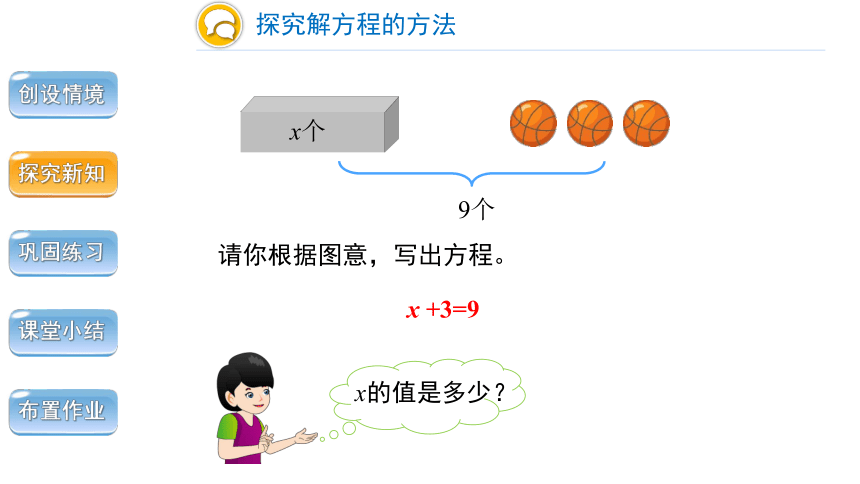
请你根据图意,写出方程。
x个
x +3=9
9个
x的值是多少?
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
探究解方程的方法
x +3=9
x个
9个
一眼就看出6+3=9,所以 x=6。
两个数相加等于9,一个加数是3,另一个加数就是9-3=6。x=6。
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
探究解方程的方法
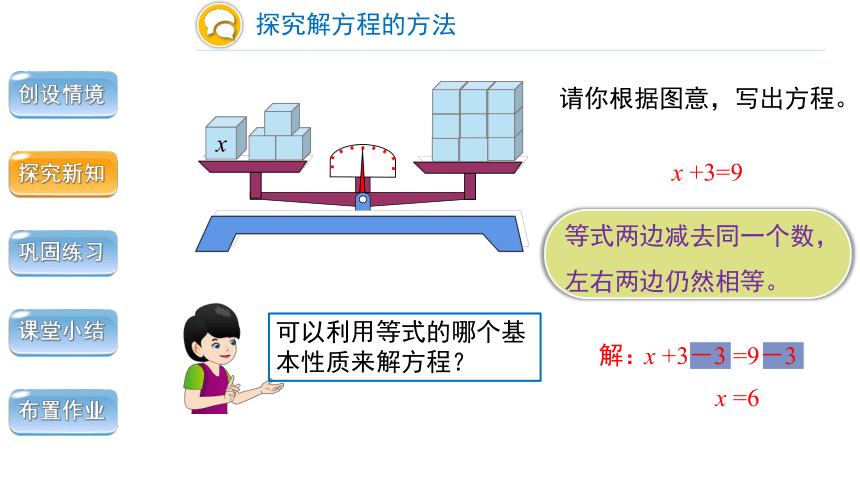
请你根据图意,写出方程。
x +3=9
x =6
解:
x
等式两边减去同一个数,左右两边仍然相等。
可以利用等式的哪个基本性质来解方程?
x +3-3 =9-3
x +3-3=9-3
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
探究解方程的方法
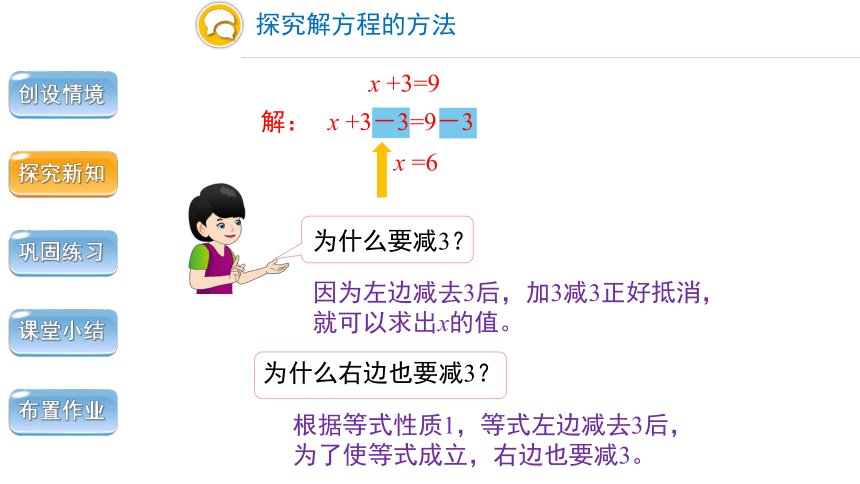
x +3=9
x =6
解:
因为左边减去3后,加3减3正好抵消,就可以求出x的值。
根据等式性质1,等式左边减去3后,为了使等式成立,右边也要减3。
为什么要减3?
为什么右边也要减3?
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
探究解方程的方法
x +3=9
x +3-3=9-3
x =6
解:
方程的解
解方程
(1)使方程左右两边相等的未知数的值,叫做方程的解。
(2)求方程解的过程叫做解方程。
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
探究解方程的方法
x +3=9
x +3-3=9-3
x =6
解:
检验:
方程左边= x +3
=6+3
=9
=方程右边
所以, x =6是方程的解。
x =6是不是正确的答案呢?检验一下。
小结:在解方程时,需要先写一个“解”字,解方程过程中写的都是等式,而不是递等式。而且每一步的等号上下要对齐。
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
探究解方程的方法
请你根据图意,写出方程。
3x = 18
x
x
等式的左边有3个x,而解方程的目标是要得到一个x的值。因此,可以在左边除以3,3x÷3就可以得到一个x,为了保持左右相等,右边也要除以3,18÷3得到6。因此,x=6。
x
怎样求出x的值。
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
探究解方程的方法
3x = 18
x
x
x
3x÷( )= 18÷( )
x = 6
解:
等式两边除以同一个不等于0的数,左右两边仍然相等。
3
3
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
解方程的依据
小组讨论,例1和例2的解方程依据为什么不一样呢?
因为例1中x参与的是加法运算,而例2中x参与的是乘法运算。因此,x参与的运算不同,选择的等式性质也不同。
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
探究检验方法
3x =18
3x÷3=18÷3
x =6
解:
检验:
方程左边= 3x
=3×6
=18
=方程右边
所以, x =6是方程的解。
请你检验一下。
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
探究解方程的方法
解方程 20-x = 9
你们在解方程的过程中遇到了什么困难?
我的两边同时减去20,左边是-x,算不下去了。
20-x-20 = 9-20
解:
解方程
20-x = 9
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
原来20个
拿走x个
拿来x个
x
原来20个
x
借助天平图,解答
20-x+x =9+x
20 = 9+x
9+x=20
9+x-9=20-9
x=11
特殊方程
普通方程
转化
解:
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
探究解方程的方法
请你口头检验一下方程的解是否正确。
把 x = 11代入方程,20减去11等于9,等式右边正好也是9,所以 x = 11是方程的解。
20-x = 9
20- x+ x = 9+x
20 = 9+x
9+x = 20
9+x-9 = 20-9
x = 11
解:
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
探究解方程的方法
解方程需要注意什么?
1.解方程时必须写“解”字。
2.因为解方程时每一步得到的都是一个等式,不是递等式,所以等号要对齐。
输入标题
课堂小结
布置作业
创设情境
巩固练习
探究新知
1.解下列方程。
练习
x -23= 57
解:x -23+23= 57+23
x = 80
解:1.6x÷1.6= 9.6÷1.6
x =6
45÷x = 9
解:45÷x× x = 9× x
45 = 9 x
9 x = 45
9 x ÷9 = 45÷9
x = 5
1.6x = 9.6
说一说第3题怎么解?
这道题和例3一样,两边先同时乘x,先把这个特殊方程转化为普通方程再解。
课堂小结
布置作业
创设情境
巩固练习
探究新知
练习
x- 4.2= 3.81
解: x-4.2+4.2 = 3.81+4.2
x = 8.01
6÷x = 1.2
6 = 1.2x
解: 6÷x×x = 1.2×x
6÷x = 1.2
解 : 6÷x÷6 =1.2÷6
x =0.2
2 改正下题中的错误。
x -4.2 = 3.81
解: x-4.2+4.2 = 3.81+3.81
x = 7.62
改正
1.2x = 6
1.2x÷1.2 = 6÷1.2
x = 5
课堂小结
布置作业
创设情境
巩固练习
探究新知
3. 根据题目中的数量关系列出方程,并求出方程的解。
练习
x 元
x 元
x 元
210元
3x = 210
解: 3x÷3 = 210÷3
x = 70
x+60 = 240
x = 180
解: x+60-60 = 240-60
输入标题
布置作业
创设情境
巩固练习
课堂小结
探究新知
你有什么收获?
1.知道了解方程的依据是等式的基本性质。
2.解方程时,要写“解”字,每一步都是一个方程,上下等号要对齐。遇到特殊方程需要用x去抵消,转化为普通方程后再求解。
输入标题
创设情境
巩固练习
课堂小结
布置作业
探究新知
教材P67做一做第1题、第2题
教材P70第1题
再见
解简单方程
第五单元 简易方程
输入标题
学习目标
在解方程的过程中,培养学生的观察、分析能力,体会到知识间的密切联系,激发学习兴趣。
结合图例,理解用等式性质解方程的方法,学会正确解方程和规范书写格式。
解简单方程
输入标题
探究新知
创设情境
巩固练习
课堂小结
布置作业
什么是等式的基本性质?
问题
等式的基本性质(乘除):
等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
等式的基本性质(加减):
等式两边加上或减去同一个数,左右两边仍然相等。
输入标题
探究新知
创设情境
巩固练习
课堂小结
布置作业
问题
等式的基本性质在方程中同样适用吗?为什么?
同样适用,因为方程也是等式。
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
探究解方程的方法
请你根据图意,写出方程。
x个
x +3=9
9个
x的值是多少?
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
探究解方程的方法
x +3=9
x个
9个
一眼就看出6+3=9,所以 x=6。
两个数相加等于9,一个加数是3,另一个加数就是9-3=6。x=6。
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
探究解方程的方法
请你根据图意,写出方程。
x +3=9
x =6
解:
x
等式两边减去同一个数,左右两边仍然相等。
可以利用等式的哪个基本性质来解方程?
x +3-3 =9-3
x +3-3=9-3
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
探究解方程的方法
x +3=9
x =6
解:
因为左边减去3后,加3减3正好抵消,就可以求出x的值。
根据等式性质1,等式左边减去3后,为了使等式成立,右边也要减3。
为什么要减3?
为什么右边也要减3?
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
探究解方程的方法
x +3=9
x +3-3=9-3
x =6
解:
方程的解
解方程
(1)使方程左右两边相等的未知数的值,叫做方程的解。
(2)求方程解的过程叫做解方程。
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
探究解方程的方法
x +3=9
x +3-3=9-3
x =6
解:
检验:
方程左边= x +3
=6+3
=9
=方程右边
所以, x =6是方程的解。
x =6是不是正确的答案呢?检验一下。
小结:在解方程时,需要先写一个“解”字,解方程过程中写的都是等式,而不是递等式。而且每一步的等号上下要对齐。
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
探究解方程的方法
请你根据图意,写出方程。
3x = 18
x
x
等式的左边有3个x,而解方程的目标是要得到一个x的值。因此,可以在左边除以3,3x÷3就可以得到一个x,为了保持左右相等,右边也要除以3,18÷3得到6。因此,x=6。
x
怎样求出x的值。
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
探究解方程的方法
3x = 18
x
x
x
3x÷( )= 18÷( )
x = 6
解:
等式两边除以同一个不等于0的数,左右两边仍然相等。
3
3
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
解方程的依据
小组讨论,例1和例2的解方程依据为什么不一样呢?
因为例1中x参与的是加法运算,而例2中x参与的是乘法运算。因此,x参与的运算不同,选择的等式性质也不同。
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
探究检验方法
3x =18
3x÷3=18÷3
x =6
解:
检验:
方程左边= 3x
=3×6
=18
=方程右边
所以, x =6是方程的解。
请你检验一下。
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
探究解方程的方法
解方程 20-x = 9
你们在解方程的过程中遇到了什么困难?
我的两边同时减去20,左边是-x,算不下去了。
20-x-20 = 9-20
解:
解方程
20-x = 9
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
原来20个
拿走x个
拿来x个
x
原来20个
x
借助天平图,解答
20-x+x =9+x
20 = 9+x
9+x=20
9+x-9=20-9
x=11
特殊方程
普通方程
转化
解:
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
探究解方程的方法
请你口头检验一下方程的解是否正确。
把 x = 11代入方程,20减去11等于9,等式右边正好也是9,所以 x = 11是方程的解。
20-x = 9
20- x+ x = 9+x
20 = 9+x
9+x = 20
9+x-9 = 20-9
x = 11
解:
输入标题
巩固练习
课堂小结
布置作业
创设情境
探究新知
探究解方程的方法
解方程需要注意什么?
1.解方程时必须写“解”字。
2.因为解方程时每一步得到的都是一个等式,不是递等式,所以等号要对齐。
输入标题
课堂小结
布置作业
创设情境
巩固练习
探究新知
1.解下列方程。
练习
x -23= 57
解:x -23+23= 57+23
x = 80
解:1.6x÷1.6= 9.6÷1.6
x =6
45÷x = 9
解:45÷x× x = 9× x
45 = 9 x
9 x = 45
9 x ÷9 = 45÷9
x = 5
1.6x = 9.6
说一说第3题怎么解?
这道题和例3一样,两边先同时乘x,先把这个特殊方程转化为普通方程再解。
课堂小结
布置作业
创设情境
巩固练习
探究新知
练习
x- 4.2= 3.81
解: x-4.2+4.2 = 3.81+4.2
x = 8.01
6÷x = 1.2
6 = 1.2x
解: 6÷x×x = 1.2×x
6÷x = 1.2
解 : 6÷x÷6 =1.2÷6
x =0.2
2 改正下题中的错误。
x -4.2 = 3.81
解: x-4.2+4.2 = 3.81+3.81
x = 7.62
改正
1.2x = 6
1.2x÷1.2 = 6÷1.2
x = 5
课堂小结
布置作业
创设情境
巩固练习
探究新知
3. 根据题目中的数量关系列出方程,并求出方程的解。
练习
x 元
x 元
x 元
210元
3x = 210
解: 3x÷3 = 210÷3
x = 70
x+60 = 240
x = 180
解: x+60-60 = 240-60
输入标题
布置作业
创设情境
巩固练习
课堂小结
探究新知
你有什么收获?
1.知道了解方程的依据是等式的基本性质。
2.解方程时,要写“解”字,每一步都是一个方程,上下等号要对齐。遇到特殊方程需要用x去抵消,转化为普通方程后再求解。
输入标题
创设情境
巩固练习
课堂小结
布置作业
探究新知
教材P67做一做第1题、第2题
教材P70第1题
再见
