第18章图形的相似18.3《相似三角形的性质》(第三课时)[下学期]
文档属性
| 名称 | 第18章图形的相似18.3《相似三角形的性质》(第三课时)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 834.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-08-22 00:00:00 | ||
图片预览




文档简介
课件27张PPT。相似三角形的性质卓山中学初二数学备课组课前复习:(1)什么叫相似三角形?
对应角相等、对应边成比例的三角形,叫做相似三角形.(2)如何识别两个三角形相似?①两个角对应相等;
②两边对应成比例,且夹角相等;
③三边对应成比例.ABCA/B/C/ ①相似三角形的对应角_____________
②相似三角形的对应边______________想一想: 它们还有哪些性质呢?课前复习:(3)相似三角形有何特征?一个三角形有三条重要线段:
________________如果两个三角形相似,
那么这些对应线段有什么关系呢?情境引入高、中线、角平分线学习目标1、在理解相似三角形特征的基础上,掌握相似三角形对应高、对应中线、对应角平分线、周长、面积的比等性质.
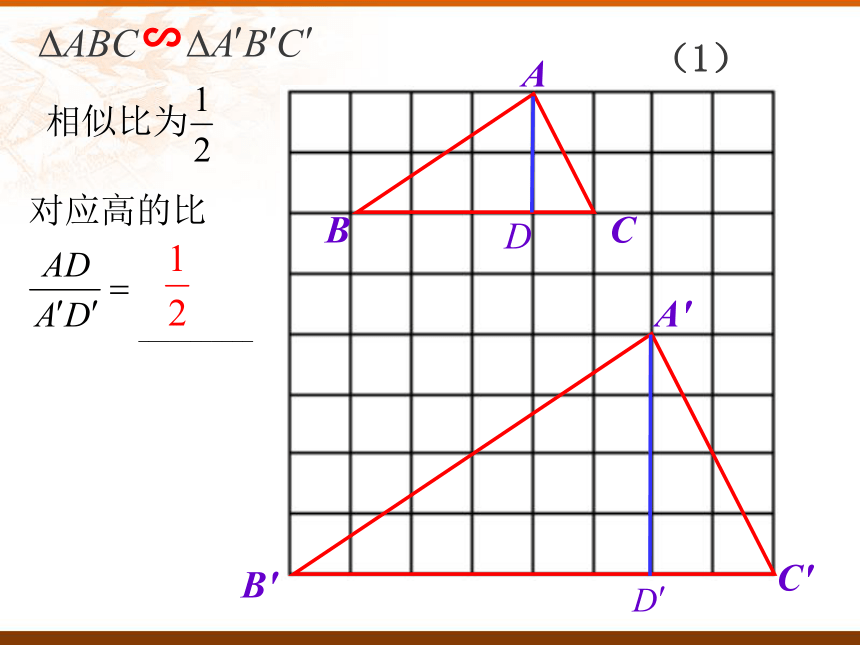
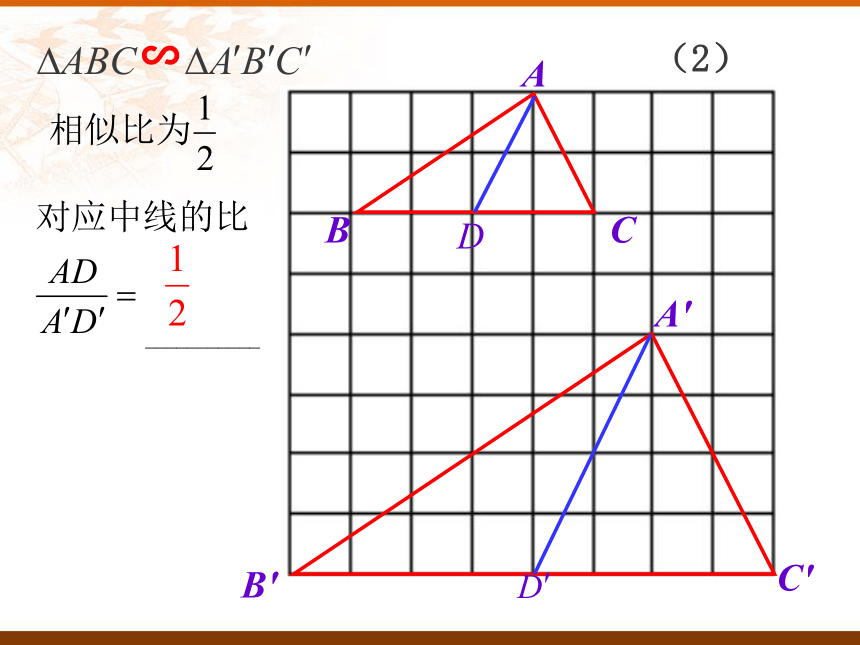
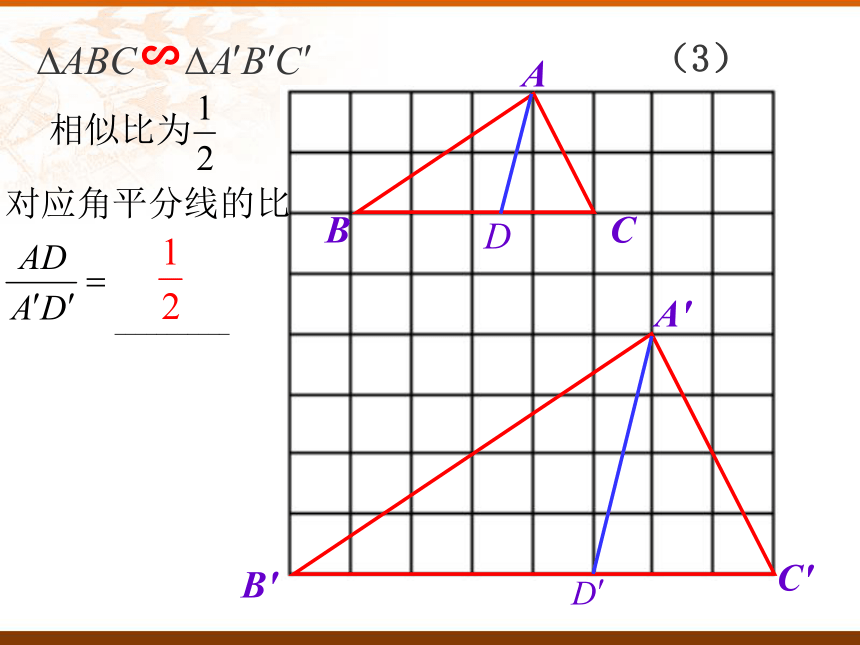
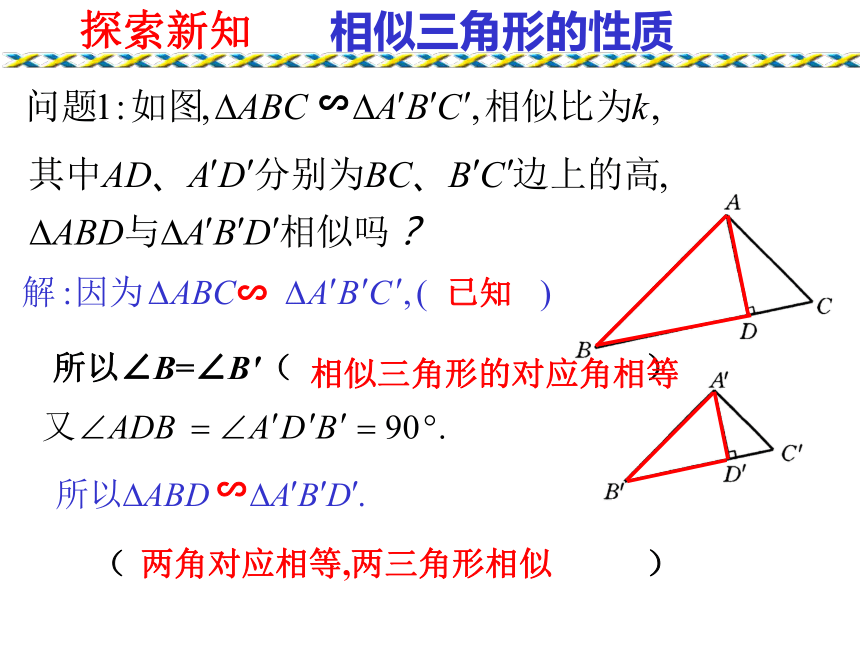
2、通过实践体会相似三角形的性质,会用性质解决相关的问题.∽(1)∽(2)∽(3)探索新知两角对应相等,两三角形相似∽∽已知所以∠B=∠B′( )相似三角形的对应角相等 ∽( )相似三角形的性质探索新知∽所以(相似三角形的对应边成比例)∽∽相似三角形的性质结论:相似三角形对应高的比等于相似比.类似结论D'C'B'A'DCBA∽自主思考---结论:相似三角形对应中线的比等于相似比.A′C′B′CBAE′E∽类似结论自主思考---结论:相似三角形对应角的角平分线的比等于相似比.对应高的比
对应中线的比
对应角平分线的比 相
似
三
角
形都等于相似比.相似三角形的性质填一填1.相似三角形对应边的比为2∶3,那么相似比为_________,对应角的角平分线的比为______.2∶ 32 ∶ 32.两个相似三角形的相似比为0.25, 则对应高的比为_________,对应角的角平分线的比为_________. 0.250.253.两个相似三角形对应中线的比为 ,
则相似比为______,对应高的比为______ .问题: 两个相似三角形的周长比
会等于相似比吗?相似三角形的性质图中(1)(2)(3)分别是边长为1、2、3的等边三角形,它们都相似吗?(1)(2)(3)123用心观察(1)与(2)的相似比=______,
(1)与(2)的周长比=______
(2)与(3)的相似比=______,
(2)与(3)的周长比=______1∶ 2结论: 相似三角形的周长比等于______.相似比(都相似)3∶ 62∶ 36∶ 9=1∶ 2=2∶ 3对应高的比
对应中线的比
对应角平分线的比
周长的比 相
似
三
角
形都等于相似比.相似三角形的性质问题:两个相似三角形的面积
之间有什么关系呢?相似三角形的性质用心观察1231∶ 2当相似比=k时,面积比=k2. (1)(2)(3)(1)与(2)的相似比=______,
(1)与(2)的面积比=______
(2)与(3)的相似比=______,
(2)与(3)的面积比=______1∶ 42∶ 34∶ 9相似三角形面积的比等于相似比的平方.对应高的比
对应中线的比
对应角平分线的比
周长的比 相
似
三
角
形都等于相似比.面积的比等于相似比的平方相似三角形的性质1.如果两个三角形相似,相似比为3∶5,则对应角的角平分线的比等于______.2.相似三角形对应边的比为0.4,
那么相似比为_______,
对应角的角平分线的比为______,
周长的比为_________,
面积的比为_________.3∶5 0.4P79当堂训练0.40.40.163.如图,在正方形网格上有△A1B1C1和△A2B2C2 ,这两个三角形相似吗?
如果相似,求出△A1B1C1和△A2B2C2的面积比.2 : 1解:相似.因为相似比是
所以面积比是4 : 1P79当堂训练 (1)△ADE与△ABC相似吗?如果相似, 求它们的相似比. ABCDE1∶4 (2) △ADE的周长︰△ABC的周长=_______. 1∶4 例1、如图,DE∥BC, DE = 1, BC = 4,例题赏析例2、如图,在 ABCD中,若E是AB的中点,
则(1)?AEF与?CDF的相似比为______.
(2)若?AEF的面积为5 cm2,
则?CDF的面积为______.BFEDCA例题赏析1 : 220 cm2 1、相似三角形对应边成____,对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线的比都等于________.
3、相似三角形周长的比等于________,
相似三角形面积的比等于______________.
课堂小结相似比的平方相似三角形的性质相似多边形也有同样的结论1、已知两个等边三角形的边长之比为 2 :3,且它们的面积之和为26cm2,则较小的等边三角形的面积为多少?拓展训练拓展训练2、平行四边形ABCD与平行四边形 相似,已知AB=5,对应边 =6,平行四边形
ABCD的面积为10,求平行四边形的面积.
对应角相等、对应边成比例的三角形,叫做相似三角形.(2)如何识别两个三角形相似?①两个角对应相等;
②两边对应成比例,且夹角相等;
③三边对应成比例.ABCA/B/C/ ①相似三角形的对应角_____________
②相似三角形的对应边______________想一想: 它们还有哪些性质呢?课前复习:(3)相似三角形有何特征?一个三角形有三条重要线段:
________________如果两个三角形相似,
那么这些对应线段有什么关系呢?情境引入高、中线、角平分线学习目标1、在理解相似三角形特征的基础上,掌握相似三角形对应高、对应中线、对应角平分线、周长、面积的比等性质.
2、通过实践体会相似三角形的性质,会用性质解决相关的问题.∽(1)∽(2)∽(3)探索新知两角对应相等,两三角形相似∽∽已知所以∠B=∠B′( )相似三角形的对应角相等 ∽( )相似三角形的性质探索新知∽所以(相似三角形的对应边成比例)∽∽相似三角形的性质结论:相似三角形对应高的比等于相似比.类似结论D'C'B'A'DCBA∽自主思考---结论:相似三角形对应中线的比等于相似比.A′C′B′CBAE′E∽类似结论自主思考---结论:相似三角形对应角的角平分线的比等于相似比.对应高的比
对应中线的比
对应角平分线的比 相
似
三
角
形都等于相似比.相似三角形的性质填一填1.相似三角形对应边的比为2∶3,那么相似比为_________,对应角的角平分线的比为______.2∶ 32 ∶ 32.两个相似三角形的相似比为0.25, 则对应高的比为_________,对应角的角平分线的比为_________. 0.250.253.两个相似三角形对应中线的比为 ,
则相似比为______,对应高的比为______ .问题: 两个相似三角形的周长比
会等于相似比吗?相似三角形的性质图中(1)(2)(3)分别是边长为1、2、3的等边三角形,它们都相似吗?(1)(2)(3)123用心观察(1)与(2)的相似比=______,
(1)与(2)的周长比=______
(2)与(3)的相似比=______,
(2)与(3)的周长比=______1∶ 2结论: 相似三角形的周长比等于______.相似比(都相似)3∶ 62∶ 36∶ 9=1∶ 2=2∶ 3对应高的比
对应中线的比
对应角平分线的比
周长的比 相
似
三
角
形都等于相似比.相似三角形的性质问题:两个相似三角形的面积
之间有什么关系呢?相似三角形的性质用心观察1231∶ 2当相似比=k时,面积比=k2. (1)(2)(3)(1)与(2)的相似比=______,
(1)与(2)的面积比=______
(2)与(3)的相似比=______,
(2)与(3)的面积比=______1∶ 42∶ 34∶ 9相似三角形面积的比等于相似比的平方.对应高的比
对应中线的比
对应角平分线的比
周长的比 相
似
三
角
形都等于相似比.面积的比等于相似比的平方相似三角形的性质1.如果两个三角形相似,相似比为3∶5,则对应角的角平分线的比等于______.2.相似三角形对应边的比为0.4,
那么相似比为_______,
对应角的角平分线的比为______,
周长的比为_________,
面积的比为_________.3∶5 0.4P79当堂训练0.40.40.163.如图,在正方形网格上有△A1B1C1和△A2B2C2 ,这两个三角形相似吗?
如果相似,求出△A1B1C1和△A2B2C2的面积比.2 : 1解:相似.因为相似比是
所以面积比是4 : 1P79当堂训练 (1)△ADE与△ABC相似吗?如果相似, 求它们的相似比. ABCDE1∶4 (2) △ADE的周长︰△ABC的周长=_______. 1∶4 例1、如图,DE∥BC, DE = 1, BC = 4,例题赏析例2、如图,在 ABCD中,若E是AB的中点,
则(1)?AEF与?CDF的相似比为______.
(2)若?AEF的面积为5 cm2,
则?CDF的面积为______.BFEDCA例题赏析1 : 220 cm2 1、相似三角形对应边成____,对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线的比都等于________.
3、相似三角形周长的比等于________,
相似三角形面积的比等于______________.
课堂小结相似比的平方相似三角形的性质相似多边形也有同样的结论1、已知两个等边三角形的边长之比为 2 :3,且它们的面积之和为26cm2,则较小的等边三角形的面积为多少?拓展训练拓展训练2、平行四边形ABCD与平行四边形 相似,已知AB=5,对应边 =6,平行四边形
ABCD的面积为10,求平行四边形的面积.
