广西河池市八校2022-2023学年高一下学期第一次联考(4月)数学试题(Word版含答案)
文档属性
| 名称 | 广西河池市八校2022-2023学年高一下学期第一次联考(4月)数学试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 858.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-03 17:08:25 | ||
图片预览




文档简介
河池市八校2022-2023学年高一下学期第一次联考
数学
一、选择题:本大题共8小题,每小题5分.共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,,则( )
A. B. C. D.
2.在复平面内,若复数对应的点的坐标为,则( )
A. B. C. D.
3.已知点是第三象限的点,则的终边位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.( )
A. B. C. D.
5.某三角形直观图是面积为2的等边三角形,则原三角形的面积为( )
A. B. C. D.
6.若向量,,且,则( )
A. B. C. D.
7.已知复数(i是虚数单位),则( )
A. B. C.10 D.34
8.在中,已知,,,则角A的度数为( )
A.60° B.120° C.60或120° D.90°
二、选择题:本题共4小题,每小题5分.共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9.在正方体的8个顶点中任意取4个不同的顶点,则下列说法正确的是( )
A.存在四个点,使得这四个点构成平行四边形
B.存在四个点可以构成正四面体
C.不存在这样的四个点,使得构成的四面体每个面都是直角三角形
D.存在有三个面是直角三角形、一个面是等边三角形的四面体
10.欧拉公式是由瑞士著名数学家欧拉创立,该公式将指数函数的定义域扩大到复数集,建立了三角函数与指数函数的关联,在复变函数论里面占有非常重要的地位,被誉为数学中的天桥.依据欧拉公式,下列选项中正确的是( )
A.对应的点位于第一象限 B.为纯虚数
C.的模等于 D.的共轭复数为
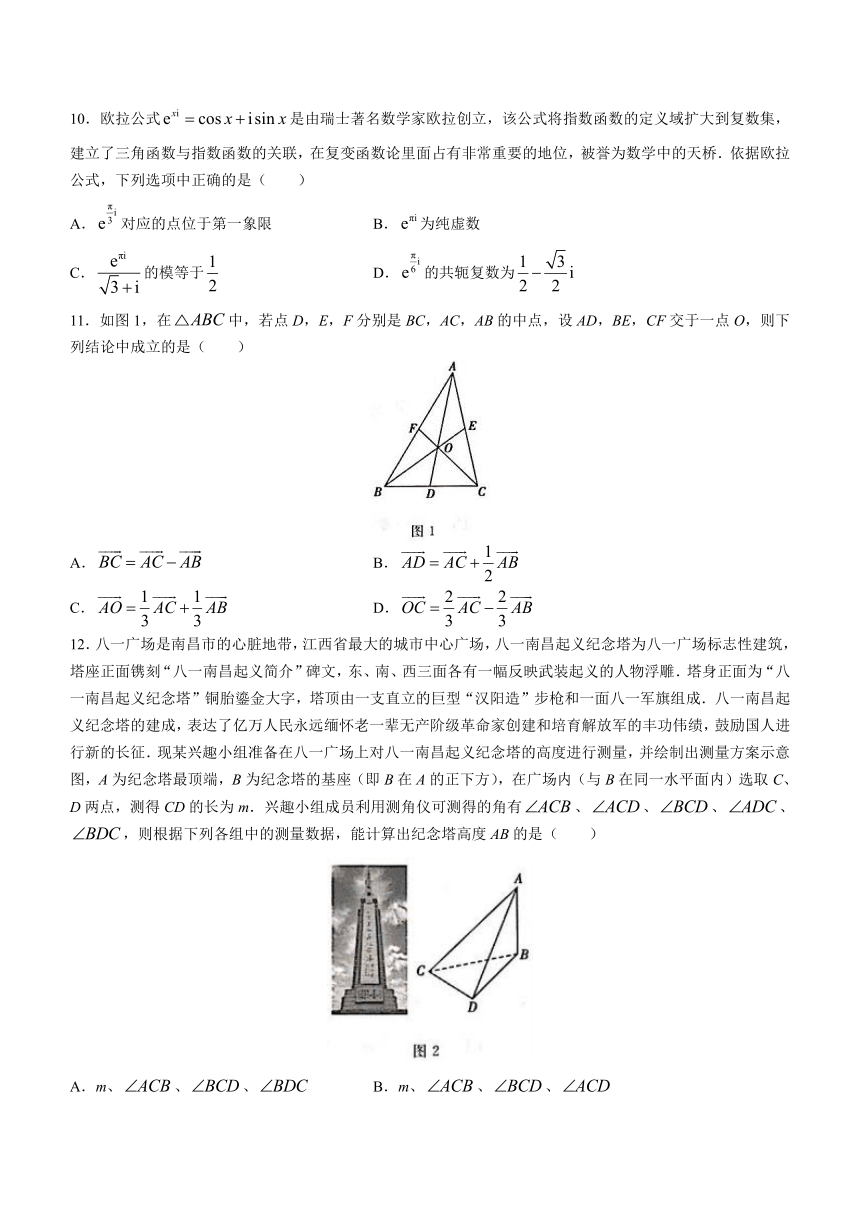
11.如图1,在中,若点D,E,F分别是BC,AC,AB的中点,设AD,BE,CF交于一点O,则下列结论中成立的是( )
A. B.
C. D.
12.八一广场是南昌市的心脏地带,江西省最大的城市中心广场,八一南昌起义纪念塔为八一广场标志性建筑,塔座正面镌刻“八一南昌起义简介”碑文,东、南、西三面各有一幅反映武装起义的人物浮雕.塔身正面为“八一南昌起义纪念塔”铜胎鎏金大字,塔顶由一支直立的巨型“汉阳造”步枪和一面八一军旗组成.八一南昌起义纪念塔的建成,表达了亿万人民永远缅怀老一辈无产阶级革命家创建和培育解放军的丰功伟绩,鼓励国人进行新的长征.现某兴趣小组准备在八一广场上对八一南昌起义纪念塔的高度进行测量,并绘制出测量方案示意图,A为纪念塔最顶端,B为纪念塔的基座(即B在A的正下方),在广场内(与B在同一水平面内)选取C、D两点,测得CD的长为m.兴趣小组成员利用测角仪可测得的角有、、、、,则根据下列各组中的测量数据,能计算出纪念塔高度AB的是( )
A.m、、、 B.m、、、
C.m、、、 D.m、、、
三、填空题(本题共4小题,每小题5分,共20分)
13.已知向量,满足,,且,的夹角为45°,则______.
14.正六棱锥底面边长为1,侧棱长为3,则棱锥高为______.
15.已知,都是复数,,的共轭复数分别为,.下列命题中,真命题的序号是______.
①若,则则;②若,则;
③如果,那么;④若,则为实数.
16.如图3,海平面上的甲船位于中心O的南偏西30°,与O相距15n mile的C处.现甲船以35n mile/h的速度沿直线CB去营救位于中心O正东方C向25n mile的B处的乙船,则甲船到达B处需要的时间为______h.
四、解答题(共70分.解答应写出文字说明、证明过程或演算步骤.)
17.(本小题满分10分)
已知复数,,其中x,y为非零实数.
(1)若是实数,求的值;
(2)若,复数为实数,求实数m的值.
18.(本小题满分12分)
已知,,.
(1)若,求k的值.
(2)若,且A,B,C三点共线,求m的值.
19.(本小题满分12分)
在中,角A,B,C的对边分别为a,b,c,若.
(1)求角C的大小;
(2)若,且的面积为,求边长c.
20.(本小题满分12分)
已知函数.
(1)求的对称中心和单调递增区间;
(2)求在区间上的最值.
21.(本小题满分12分)
“不以规矩,不能成方圆”,出自《孟子 离娄章句上》.“规”指圆规,“矩”指由相互垂直的长短两条直尺构成的角尺,是用来测量、画圆和方形图案的工具.有一块圆形木板,以“矩”量之,较长边为10 cm,较短边为5 cm,如图4所示,将这块圆形木板截出一块三角形木块,三角形顶点A,B,C都在圆周上,角A,B,C的对边分别为a,b,c,满足 cm.
(1)求;
(2)若的面积为8 cm,且,求的周长.
22.(本小题满分12分)
如图5,在直角三角形ABC中,,.点D,E分别是线段AB,BC上的点,满足,,.
(1)求的取值范围;
(2)是否存在实数,使得?若存在,求出的值;若不存在,请说明理由.
河池市八校2022-2023学年高一下学期第一次联考
数学参考答案
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B D C A C C A C ABD AC AC ACD
一、选择题:本大题共8小题,每小题5分.共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.B(因为,,所以.故应选B.)
2.D(由已知得,.故应选D.)
3.C(∵点是第三象限的点,∴,,
由可得,的终边位于第二象限或第三象限或x轴的非正半轴;
由可得,的终边位于第一象限或第三象限,
综上所述,的终边位于第三象限.故应选C.)
∴A(,故应选A.)
5.C(根据斜二测画法中直观图与原图形面积的关系求解.
由题意直观图是面积为2的等边三角形,即面积为,所以原图形的面积为.
故应选C.)
6.C(由题意得,得.故应选C.)
7.A(,
所以,故应选A.)
8.C(由题知,,,
在中,由正弦定理可得:,
解得,因为,,所以或120°故应选C.)
二、选择题:本题共4小题,每小题5分.共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得3分.
9.ABD(对于A,如图四边形为平行四边形,所以A正确,
对于B,四面体是正四面体,所以B正确,
对于C,如图四面体的每个面都是直角三角形,所以C不正确,
对于D,如图四面体的三个面是直角三角形、一个面是等边三角形,所以D正确,故应选ABD.)
10.AC(对于A:,∴对应的点位于第一象限,故A正确;
对于B:,∴为实数,故B不正确;
对于C:,故C正确;
对于D:,所以的共轭复数为,故D错误.故应选AC.)
11.AC(根据向量减法可得,故A正确;
因为D是BC的中点,所以,故B错误;
由题意知O是△ABC的重心,则,故C正确;
,故D错误.
故应选AC.)
12.ACD(对于A:由m,、可以解,又,可求塔高度AB;
对于B:在中,由,无法解三角形,在中,由,无法解三角形,
在中,已知两角、无法解三角形,所以无法解出任意三角形,故不能求塔高度AB;
对于C:由,、可以解,可求AC,又,即可求塔高度AB;
对于D:由,可求 在中,由正弦定理可求BC,
在中,由BC,可求AB.即D项可求塔高AB.故应选ACD.)
三、填空题(本题共4小题,每小题5分,共20分)
13.(因为向量,满足,,且,的夹角为45°,
所以故答案为:.)
14.(因几何体为正六棱锥,则其底面为正六边形,则底面中心O到底面一顶点B的距离,六棱锥上顶点A与底面中心连线AO为六棱锥的高,又侧棱长,
则棱锥高.故答案为:.)
15.③④(设,(a,b,c,),则,
对于①,若,则,此时不一定有(如),故①错;
对于②,若,则,都是实数,所以,若,,则,故②错;
对于③,令,x,,则,如果,即,
则,故③正确;
对于④,若,则,所以,故④正确.故答案为:③④.)
16.1(如图所示,
中,,,;
所以,
即,又甲船的速度为35n mile/h,
所以甲船到达B处需要的时间为(h).故答案为:1.)
四、解答题(共70分.解答应写出文字说明、证明过程或演算步骤.)
17.(1)∵为实数,
∴,又∵x,y为非零实数,∴.
(2)∵,∴,
∴为实数,
∴ ∴m的值为-2.
18.(1) 因为,
所以 解得
(2)因为A,B,C三点共线,a与b不共线,
所以存在实数,使得,即,
整理得,所以,解得,故m的值为.
19.(1)由正弦定理得:,
∴,
∵,∴,∴,则.
(2)∵的面积为,则
∴根据题意得,则或
若,则为等边三角形,;
若,则,即 ∴或.
20.(1)令,,则,.
所以的对称中心为,
由,解得,
所以的增区间为,
(2)令,由知,
所以要求在区间上的最值,即求在上的最值,
当时,,当时,,所以,.
21.(1)设的外接圆半径为R,则(cm),
由正弦定理,可得.
(2)∵,则,故C为锐角,∴,
由面积公式,即,可得,
由余弦定理,即,
可得,解得(cm),故的周长为(cm).
22.(1)在直角三角形ABC中,,.
∴,,,
,
∵,∴.
(2)
令,得或(舍)(舍).
∴存在实数,使得.
数学
一、选择题:本大题共8小题,每小题5分.共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,,则( )
A. B. C. D.
2.在复平面内,若复数对应的点的坐标为,则( )
A. B. C. D.
3.已知点是第三象限的点,则的终边位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.( )
A. B. C. D.
5.某三角形直观图是面积为2的等边三角形,则原三角形的面积为( )
A. B. C. D.
6.若向量,,且,则( )
A. B. C. D.
7.已知复数(i是虚数单位),则( )
A. B. C.10 D.34
8.在中,已知,,,则角A的度数为( )
A.60° B.120° C.60或120° D.90°
二、选择题:本题共4小题,每小题5分.共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9.在正方体的8个顶点中任意取4个不同的顶点,则下列说法正确的是( )
A.存在四个点,使得这四个点构成平行四边形
B.存在四个点可以构成正四面体
C.不存在这样的四个点,使得构成的四面体每个面都是直角三角形
D.存在有三个面是直角三角形、一个面是等边三角形的四面体
10.欧拉公式是由瑞士著名数学家欧拉创立,该公式将指数函数的定义域扩大到复数集,建立了三角函数与指数函数的关联,在复变函数论里面占有非常重要的地位,被誉为数学中的天桥.依据欧拉公式,下列选项中正确的是( )
A.对应的点位于第一象限 B.为纯虚数
C.的模等于 D.的共轭复数为
11.如图1,在中,若点D,E,F分别是BC,AC,AB的中点,设AD,BE,CF交于一点O,则下列结论中成立的是( )
A. B.
C. D.
12.八一广场是南昌市的心脏地带,江西省最大的城市中心广场,八一南昌起义纪念塔为八一广场标志性建筑,塔座正面镌刻“八一南昌起义简介”碑文,东、南、西三面各有一幅反映武装起义的人物浮雕.塔身正面为“八一南昌起义纪念塔”铜胎鎏金大字,塔顶由一支直立的巨型“汉阳造”步枪和一面八一军旗组成.八一南昌起义纪念塔的建成,表达了亿万人民永远缅怀老一辈无产阶级革命家创建和培育解放军的丰功伟绩,鼓励国人进行新的长征.现某兴趣小组准备在八一广场上对八一南昌起义纪念塔的高度进行测量,并绘制出测量方案示意图,A为纪念塔最顶端,B为纪念塔的基座(即B在A的正下方),在广场内(与B在同一水平面内)选取C、D两点,测得CD的长为m.兴趣小组成员利用测角仪可测得的角有、、、、,则根据下列各组中的测量数据,能计算出纪念塔高度AB的是( )
A.m、、、 B.m、、、
C.m、、、 D.m、、、
三、填空题(本题共4小题,每小题5分,共20分)
13.已知向量,满足,,且,的夹角为45°,则______.
14.正六棱锥底面边长为1,侧棱长为3,则棱锥高为______.
15.已知,都是复数,,的共轭复数分别为,.下列命题中,真命题的序号是______.
①若,则则;②若,则;
③如果,那么;④若,则为实数.
16.如图3,海平面上的甲船位于中心O的南偏西30°,与O相距15n mile的C处.现甲船以35n mile/h的速度沿直线CB去营救位于中心O正东方C向25n mile的B处的乙船,则甲船到达B处需要的时间为______h.
四、解答题(共70分.解答应写出文字说明、证明过程或演算步骤.)
17.(本小题满分10分)
已知复数,,其中x,y为非零实数.
(1)若是实数,求的值;
(2)若,复数为实数,求实数m的值.
18.(本小题满分12分)
已知,,.
(1)若,求k的值.
(2)若,且A,B,C三点共线,求m的值.
19.(本小题满分12分)
在中,角A,B,C的对边分别为a,b,c,若.
(1)求角C的大小;
(2)若,且的面积为,求边长c.
20.(本小题满分12分)
已知函数.
(1)求的对称中心和单调递增区间;
(2)求在区间上的最值.
21.(本小题满分12分)
“不以规矩,不能成方圆”,出自《孟子 离娄章句上》.“规”指圆规,“矩”指由相互垂直的长短两条直尺构成的角尺,是用来测量、画圆和方形图案的工具.有一块圆形木板,以“矩”量之,较长边为10 cm,较短边为5 cm,如图4所示,将这块圆形木板截出一块三角形木块,三角形顶点A,B,C都在圆周上,角A,B,C的对边分别为a,b,c,满足 cm.
(1)求;
(2)若的面积为8 cm,且,求的周长.
22.(本小题满分12分)
如图5,在直角三角形ABC中,,.点D,E分别是线段AB,BC上的点,满足,,.
(1)求的取值范围;
(2)是否存在实数,使得?若存在,求出的值;若不存在,请说明理由.
河池市八校2022-2023学年高一下学期第一次联考
数学参考答案
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B D C A C C A C ABD AC AC ACD
一、选择题:本大题共8小题,每小题5分.共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.B(因为,,所以.故应选B.)
2.D(由已知得,.故应选D.)
3.C(∵点是第三象限的点,∴,,
由可得,的终边位于第二象限或第三象限或x轴的非正半轴;
由可得,的终边位于第一象限或第三象限,
综上所述,的终边位于第三象限.故应选C.)
∴A(,故应选A.)
5.C(根据斜二测画法中直观图与原图形面积的关系求解.
由题意直观图是面积为2的等边三角形,即面积为,所以原图形的面积为.
故应选C.)
6.C(由题意得,得.故应选C.)
7.A(,
所以,故应选A.)
8.C(由题知,,,
在中,由正弦定理可得:,
解得,因为,,所以或120°故应选C.)
二、选择题:本题共4小题,每小题5分.共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得3分.
9.ABD(对于A,如图四边形为平行四边形,所以A正确,
对于B,四面体是正四面体,所以B正确,
对于C,如图四面体的每个面都是直角三角形,所以C不正确,
对于D,如图四面体的三个面是直角三角形、一个面是等边三角形,所以D正确,故应选ABD.)
10.AC(对于A:,∴对应的点位于第一象限,故A正确;
对于B:,∴为实数,故B不正确;
对于C:,故C正确;
对于D:,所以的共轭复数为,故D错误.故应选AC.)
11.AC(根据向量减法可得,故A正确;
因为D是BC的中点,所以,故B错误;
由题意知O是△ABC的重心,则,故C正确;
,故D错误.
故应选AC.)
12.ACD(对于A:由m,、可以解,又,可求塔高度AB;
对于B:在中,由,无法解三角形,在中,由,无法解三角形,
在中,已知两角、无法解三角形,所以无法解出任意三角形,故不能求塔高度AB;
对于C:由,、可以解,可求AC,又,即可求塔高度AB;
对于D:由,可求 在中,由正弦定理可求BC,
在中,由BC,可求AB.即D项可求塔高AB.故应选ACD.)
三、填空题(本题共4小题,每小题5分,共20分)
13.(因为向量,满足,,且,的夹角为45°,
所以故答案为:.)
14.(因几何体为正六棱锥,则其底面为正六边形,则底面中心O到底面一顶点B的距离,六棱锥上顶点A与底面中心连线AO为六棱锥的高,又侧棱长,
则棱锥高.故答案为:.)
15.③④(设,(a,b,c,),则,
对于①,若,则,此时不一定有(如),故①错;
对于②,若,则,都是实数,所以,若,,则,故②错;
对于③,令,x,,则,如果,即,
则,故③正确;
对于④,若,则,所以,故④正确.故答案为:③④.)
16.1(如图所示,
中,,,;
所以,
即,又甲船的速度为35n mile/h,
所以甲船到达B处需要的时间为(h).故答案为:1.)
四、解答题(共70分.解答应写出文字说明、证明过程或演算步骤.)
17.(1)∵为实数,
∴,又∵x,y为非零实数,∴.
(2)∵,∴,
∴为实数,
∴ ∴m的值为-2.
18.(1) 因为,
所以 解得
(2)因为A,B,C三点共线,a与b不共线,
所以存在实数,使得,即,
整理得,所以,解得,故m的值为.
19.(1)由正弦定理得:,
∴,
∵,∴,∴,则.
(2)∵的面积为,则
∴根据题意得,则或
若,则为等边三角形,;
若,则,即 ∴或.
20.(1)令,,则,.
所以的对称中心为,
由,解得,
所以的增区间为,
(2)令,由知,
所以要求在区间上的最值,即求在上的最值,
当时,,当时,,所以,.
21.(1)设的外接圆半径为R,则(cm),
由正弦定理,可得.
(2)∵,则,故C为锐角,∴,
由面积公式,即,可得,
由余弦定理,即,
可得,解得(cm),故的周长为(cm).
22.(1)在直角三角形ABC中,,.
∴,,,
,
∵,∴.
(2)
令,得或(舍)(舍).
∴存在实数,使得.
同课章节目录
