相似三角形的性质[下学期]
图片预览



文档简介
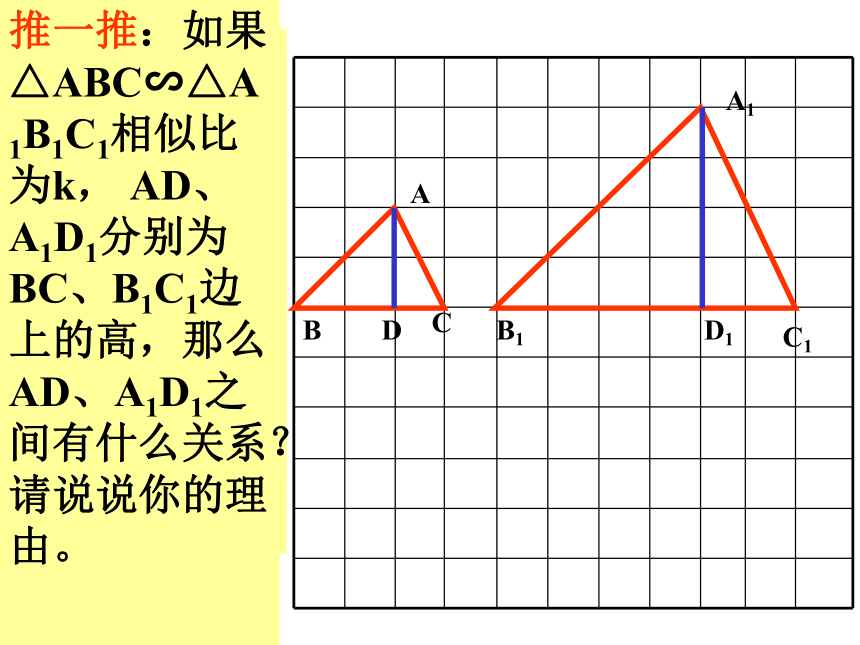
课件16张PPT。18.3.3相似三角形的性质画一画:请你在课本后面的方格纸图中,画出两个相似但不全等的三角形,再画一组对应高。 量一量:你画的两个相似三角形的相似比是多少?对应高AD与A1D1的比是多少?相似比与对应高的比相等吗? 推一推:如果△ABC∽△A1B1C1相似比为k, AD、A1D1分别为BC、B1C1边上的高,那么AD、A1D1之间有什么关系?请说说你的理由。
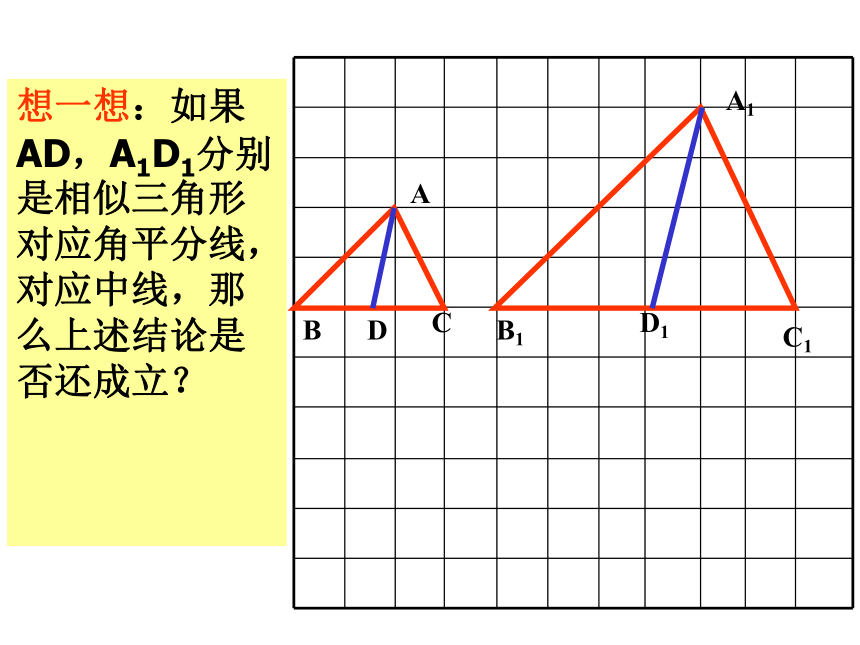
想一想:如果AD,A1D1分别是相似三角形对应角平分线,对应中线,那么上述结论是否还成立?
1、相似三角形对应高的比等于相似比;
2、相似三角形对应中线的比等于相似比;
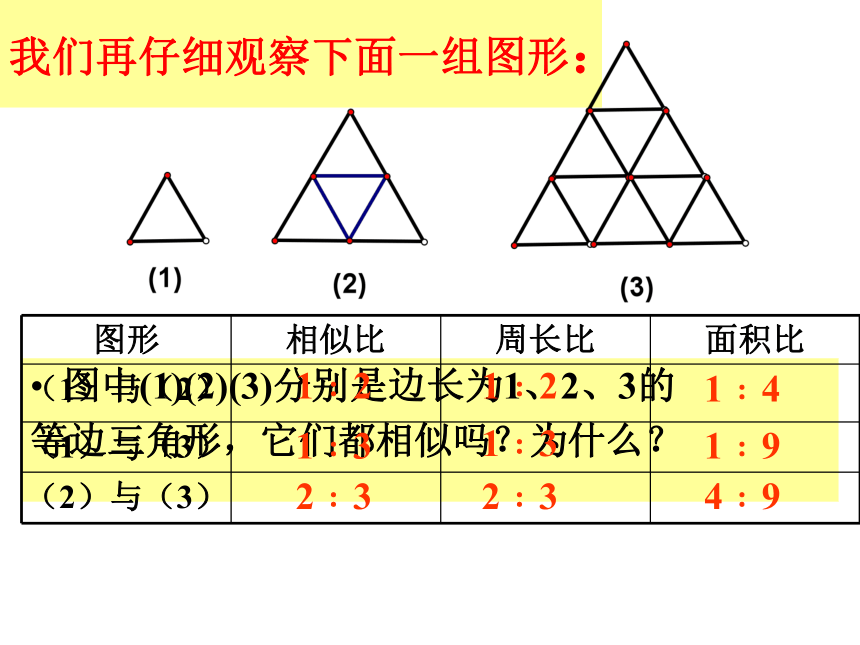
3、相似三角形对应角平分线的比等于相似比。相似三角形的性质:我们再仔细观察下面一组图形:图中(1)(2)(3)分别是边长为1、2、3的
等边三角形,它们都相似吗?为什么?
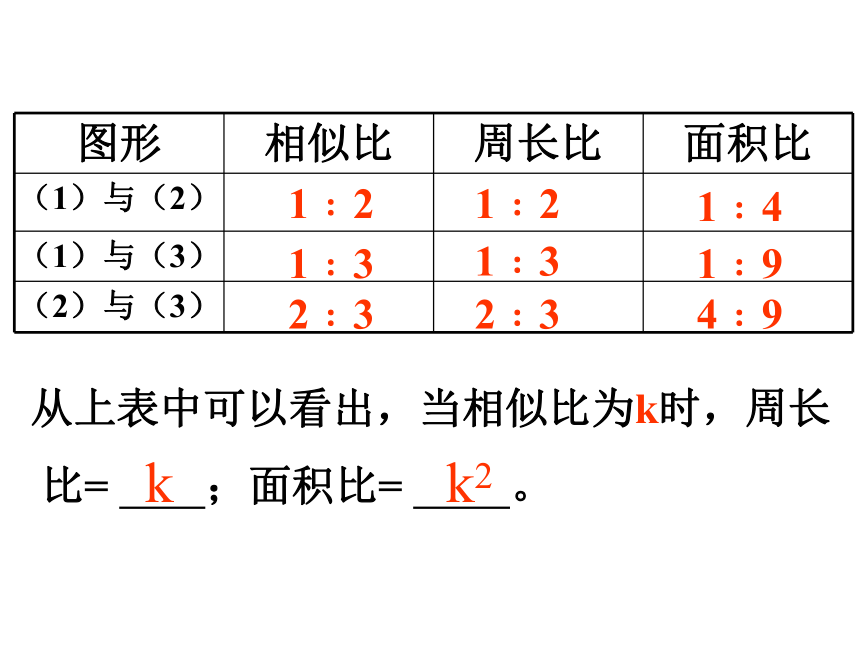
1﹕21﹕21﹕41﹕31﹕31﹕92﹕32﹕34﹕9从上表中可以看出,当相似比为k时,周长
比= ;面积比= 。kk21、相似三角形对应高的比等于相似比。
2、相似三角形对应中线的比等于相似比。
3、相似三角形对应角平分线的比等于相似比。相似三角形的性质:4、相似三角形周长的比等于相似比。
5、相似三角形面积的比等于相似比的平方。提示:相似多边形和相似三角形有同样的
性质。试一试:1、相似三角形对应边的比为3∶5 ,那么相似比为_________,对应角的角平分线的比为______,对应边的中线比为_______,周长的比为_____,面积的比为_______。3∶53∶53∶59∶253∶52、把一个三角形扩大成和它相似的三角形,
(1)如果把边长扩大为原来的10倍,那么面积扩大为原来的 倍。
(2)如果把面积扩大为原来的10倍,则边长应扩大为原来的 倍。100试一试:3、两个相似三角形对应的中线长分别是6cm和18cm,若较大三角形的周长是42cm,面积是12cm2,则较小三角形
的周长是 cm,面积 cm2。14试一试:4、如图,DF∥EG∥BC,且AD=DE=EB,则△ABC被分成的三部分的面积比S1:S2:S3为 。 S3BEDFGCS2AS1试一试:5、如图,△ABC中,点D,E,F分别在边AB,
AC,BC上,DF∥BC, EF∥AB ,
AF:FC=2 :3,S△ABC=S,
求平行四边形BEFD的面积。 试一试:ADEFBC6、如图;△ABC中,D为BC上一点,CE⊥AB于E,CF⊥AD于F,且AC:CD=BC:AC=k,试说明CE:CF=k.试一试:如图,已知梯形ABCD中,△ADM的面积为1,△CBM的面积为4,试求出图中尽可能多的三角形的面积。思维训练 你能说说今天在数学知识方面有哪些收获吗?小结:作业
1、数学作业本(1) P21
2、轻松30分 P61
3、预习18.3.4
想一想:如果AD,A1D1分别是相似三角形对应角平分线,对应中线,那么上述结论是否还成立?
1、相似三角形对应高的比等于相似比;
2、相似三角形对应中线的比等于相似比;
3、相似三角形对应角平分线的比等于相似比。相似三角形的性质:我们再仔细观察下面一组图形:图中(1)(2)(3)分别是边长为1、2、3的
等边三角形,它们都相似吗?为什么?
1﹕21﹕21﹕41﹕31﹕31﹕92﹕32﹕34﹕9从上表中可以看出,当相似比为k时,周长
比= ;面积比= 。kk21、相似三角形对应高的比等于相似比。
2、相似三角形对应中线的比等于相似比。
3、相似三角形对应角平分线的比等于相似比。相似三角形的性质:4、相似三角形周长的比等于相似比。
5、相似三角形面积的比等于相似比的平方。提示:相似多边形和相似三角形有同样的
性质。试一试:1、相似三角形对应边的比为3∶5 ,那么相似比为_________,对应角的角平分线的比为______,对应边的中线比为_______,周长的比为_____,面积的比为_______。3∶53∶53∶59∶253∶52、把一个三角形扩大成和它相似的三角形,
(1)如果把边长扩大为原来的10倍,那么面积扩大为原来的 倍。
(2)如果把面积扩大为原来的10倍,则边长应扩大为原来的 倍。100试一试:3、两个相似三角形对应的中线长分别是6cm和18cm,若较大三角形的周长是42cm,面积是12cm2,则较小三角形
的周长是 cm,面积 cm2。14试一试:4、如图,DF∥EG∥BC,且AD=DE=EB,则△ABC被分成的三部分的面积比S1:S2:S3为 。 S3BEDFGCS2AS1试一试:5、如图,△ABC中,点D,E,F分别在边AB,
AC,BC上,DF∥BC, EF∥AB ,
AF:FC=2 :3,S△ABC=S,
求平行四边形BEFD的面积。 试一试:ADEFBC6、如图;△ABC中,D为BC上一点,CE⊥AB于E,CF⊥AD于F,且AC:CD=BC:AC=k,试说明CE:CF=k.试一试:如图,已知梯形ABCD中,△ADM的面积为1,△CBM的面积为4,试求出图中尽可能多的三角形的面积。思维训练 你能说说今天在数学知识方面有哪些收获吗?小结:作业
1、数学作业本(1) P21
2、轻松30分 P61
3、预习18.3.4
